# 特性 這篇文檔是對 LightGBM 的特點和其中用到的算法的簡短介紹 本頁不包含詳細的算法，如果你對這些算法感興趣可以查閱引用的論文或者源代碼 ## 速度和內存使用的優化 許多提升工具對于決策樹的學習使用基于 pre-sorted 的算法 [[1, 2]](#references) (例如，在xgboost中默認的算法) ，這是一個簡單的解決方案，但是不易于優化。 LightGBM 利用基于 histogram 的算法 [[3, 4, 5]](#references)，通過將連續特征（屬性）值分段為 discrete bins 來加快訓練的速度并減少內存的使用。 如下的是基于 histogram 算法的優點： * **減少分割增益的計算量** * Pre-sorted 算法需要 `O(#data)` 次的計算 * Histogram 算法只需要計算 `O(#bins)` 次, 并且 `#bins` 遠少于 `#data` * 這個仍然需要 `O(#data)` 次來構建直方圖, 而這僅僅包含總結操作 * **通過直方圖的相減來進行進一步的加速** * 在二叉樹中可以通過利用葉節點的父節點和相鄰節點的直方圖的相減來獲得該葉節點的直方圖 * 所以僅僅需要為一個葉節點建立直方圖 (其 `#data` 小于它的相鄰節點)就可以通過直方圖的相減來獲得相鄰節點的直方圖，而這花費的代價(`O(#bins)`)很小。 * **減少內存的使用** * 可以將連續的值替換為 discrete bins。 如果 `#bins` 較小, 可以利用較小的數據類型來存儲訓練數據, 如 uint8_t。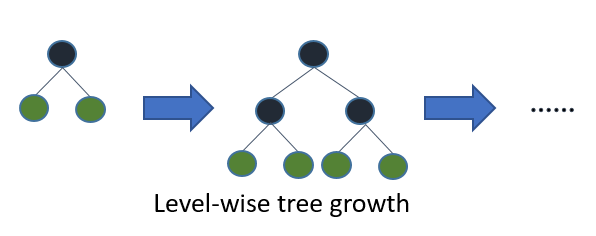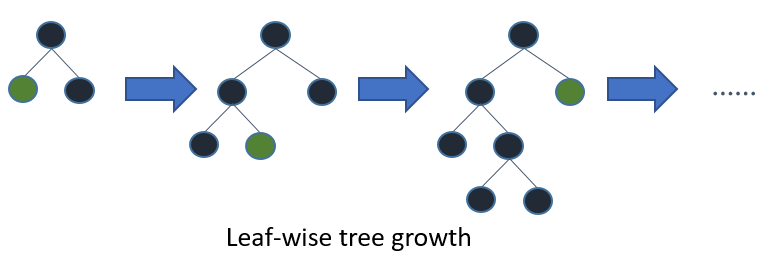 * 無需為 pre-sorting 特征值存儲額外的信息 * **減少并行學習的通信代價** ## 稀疏優化 * 對于稀疏的特征僅僅需要 `O(2 * #non_zero_data)` 來建立直方圖 ## 準確率的優化 ### Leaf-wise (Best-first) 的決策樹生長策略 大部分決策樹的學習算法通過 level(depth)-wise 策略生長樹，如下圖一樣：  LightGBM 通過 leaf-wise (best-first)[[6]](#references) 策略來生長樹。它將選取具有最大 delta loss 的葉節點來生長。 當生長相同的 `#leaf`，leaf-wise 算法可以比 level-wise 算法減少更多的損失。 當 `#data` 較小的時候，leaf-wise 可能會造成過擬合。 所以，LightGBM 可以利用額外的參數 `max_depth` 來限制樹的深度并避免過擬合（樹的生長仍然通過 leaf-wise 策略）。  ### 類別特征值的最優分割 我們通常將類別特征轉化為 one-hot coding。 然而，對于學習樹來說這不是個好的解決方案。 原因是，對于一個基數較大的類別特征，學習樹會生長的非常不平衡，并且需要非常深的深度才能來達到較好的準確率。 事實上，最好的解決方案是將類別特征劃分為兩個子集，總共有 `2^(k-1) - 1` 種可能的劃分 但是對于回歸樹 [[7]](#references) 有個有效的解決方案。為了尋找最優的劃分需要大約 `k * log(k)` . 基本的思想是根據訓練目標的相關性對類別進行重排序。 更具體的說，根據累加值(`sum_gradient / sum_hessian`)重新對（類別特征的）直方圖進行排序，然后在排好序的直方圖中尋找最好的分割點。 ## 網絡通信的優化 LightGBM 中的并行學習，僅僅需要使用一些聚合通信算法，例如 “All reduce”, “All gather” 和 “Reduce scatter”. LightGBM 實現了 state-of-art 算法 [[8]](#references) . 這些聚合通信算法可以提供比點對點通信更好的性能。 ## 并行學習的優化 LightGBM 提供以下并行學習優化算法： ### 特征并行 #### 傳統算法 傳統的特征并行算法旨在于在并行化決策樹中的“ `Find Best Split`.主要流程如下: 1. 垂直劃分數據（不同的機器有不同的特征集） 2. 在本地特征集尋找最佳劃分點 {特征, 閾值} 3. 本地進行各個劃分的通信整合并得到最佳劃分 4. 以最佳劃分方法對數據進行劃分，并將數據劃分結果傳遞給其他線程 5. 其他線程對接受到的數據進一步劃分 傳統的特征并行方法主要不足: * 存在計算上的局限，傳統特征并行無法加速 “split”（時間復雜度為 “O（#data）”）。 因此，當數據量很大的時候，難以加速。 * 需要對劃分的結果進行通信整合，其額外的時間復雜度約為 “O（#data/8）”（一個數據一個字節） #### LightGBM 中的特征并行 既然在數據量很大時，傳統數據并行方法無法有效地加速，我們做了一些改變：不再垂直劃分數據，即每個線程都持有全部數據。 因此，LighetGBM中沒有數據劃分結果之間通信的開銷，各個線程都知道如何劃分數據。 而且，“#data” 不會變得更大，所以，在使每天機器都持有全部數據是合理的。 LightGBM 中特征并行的流程如下： 1. 每個線程都在本地數據集上尋找最佳劃分點｛特征， 閾值｝ 2. 本地進行各個劃分的通信整合并得到最佳劃分 3. 執行最佳劃分 然而，該特征并行算法在數據量很大時仍然存在計算上的局限。因此，建議在數據量很大時使用數據并行。 ### 數據并行 #### 傳統算法 數據并行旨在于并行化整個決策學習過程。數據并行的主要流程如下： 1. 水平劃分數據 2. 線程以本地數據構建本地直方圖 3. 將本地直方圖整合成全局整合圖 4. 在全局直方圖中尋找最佳劃分，然后執行此劃分 傳統數據劃分的不足： * 高通訊開銷。 如果使用點對點的通訊算法，一個機器的通訊開銷大約為 “O(#machine * #feature * #bin)” 。 如果使用集成的通訊算法（例如， “All Reduce”等），通訊開銷大約為 “O(2 * #feature * #bin)”[8] 。 #### LightGBM中的數據并行 LightGBM 中采用以下方法較少數據并行中的通訊開銷： 1. 不同于“整合所有本地直方圖以形成全局直方圖”的方式，LightGBM 使用分散規約(Reduce scatter)的方式對不同線程的不同特征（不重疊的）進行整合。 然后線程從本地整合直方圖中尋找最佳劃分并同步到全局的最佳劃分中。 2. 如上所述。LightGBM 通過直方圖做差法加速訓練。 基于此，我們可以進行單葉子的直方圖通訊，并且在相鄰直方圖上使用做差法。 通過上述方法，LightGBM 將數據并行中的通訊開銷減少到 “O(0.5 * #feature * #bin)”。 ### 投票并行 投票并行未來將致力于將“數據并行”中的通訊開銷減少至常數級別。 其將會通過兩階段的投票過程較少特征直方圖的通訊開銷 [[9]](#references) . ## GPU 支持 感謝 “@huanzhang12 <[https://github.com/huanzhang12](https://github.com/huanzhang12)>” 對此項特性的貢獻。相關細節請閱讀 [[10]](#references) 。 * [GPU 安裝](./Installatn-ioGuide.rst#build-gpu-version) * [GPU 訓練](./GPU-Tutorial.rst) ## 應用和度量 支持以下應用: * 回歸，目標函數為 L2 loss * 二分類， 目標函數為 logloss（對數損失） * 多分類 * lambdarank, 目標函數為基于 NDCG 的 lambdarank 支持的度量 * L1 loss * L2 loss * Log loss * Classification error rate * AUC * NDCG * Multi class log loss * Multi class error rate 獲取更多詳情，請至 [Parameters](./Parameters.rst#metric-parameters)。 ## 其他特性 * Limit `max_depth` of tree while grows tree leaf-wise * [DART](https://arxiv.org/abs/1505.01866) * L1/L2 regularization * Bagging * Column(feature) sub-sample * Continued train with input GBDT model * Continued train with the input score file * Weighted training * Validation metric output during training * Multi validation data * Multi metrics * Early stopping (both training and prediction) * Prediction for leaf index 獲取更多詳情，請參閱 [參數](./Parameters.rst)。 ## References [1] Mehta, Manish, Rakesh Agrawal, and Jorma Rissanen. “SLIQ: A fast scalable classifier for data mining.” International Conference on Extending Database Technology. Springer Berlin Heidelberg, 1996. [2] Shafer, John, Rakesh Agrawal, and Manish Mehta. “SPRINT: A scalable parallel classifier for data mining.” Proc. 1996 Int. Conf. Very Large Data Bases. 1996. [3] Ranka, Sanjay, and V. Singh. “CLOUDS: A decision tree classifier for large datasets.” Proceedings of the 4th Knowledge Discovery and Data Mining Conference. 1998. [4] Machado, F. P. “Communication and memory efficient parallel decision tree construction.” (2003). [5] Li, Ping, Qiang Wu, and Christopher J. Burges. “Mcrank: Learning to rank using multiple classification and gradient boosting.” Advances in neural information processing systems. 2007. [6] Shi, Haijian. “Best-first decision tree learning.” Diss. The University of Waikato, 2007. [7] Walter D. Fisher. “[On Grouping for Maximum Homogeneity](http://amstat.tandfonline.com/doi/abs/10.1080/01621459.1958.10501479).” Journal of the American Statistical Association. Vol. 53, No. 284 (Dec., 1958), pp. 789-798. [8] Thakur, Rajeev, Rolf Rabenseifner, and William Gropp. “[Optimization of collective communication operations in MPICH](http://wwwi10.lrr.in.tum.de/~gerndt/home/Teaching/HPCSeminar/mpich_multi_coll.pdf).” International Journal of High Performance Computing Applications 19.1 (2005): 49-66. [9] Qi Meng, Guolin Ke, Taifeng Wang, Wei Chen, Qiwei Ye, Zhi-Ming Ma, Tieyan Liu. “[A Communication-Efficient Parallel Algorithm for Decision Tree](http://papers.nips.cc/paper/6381-a-communication-efficient-parallel-algorithm-for-decision-tree).” Advances in Neural Information Processing Systems 29 (NIPS 2016). [10] Huan Zhang, Si Si and Cho-Jui Hsieh. “[GPU Acceleration for Large-scale Tree Boosting](https://arxiv.org/abs/1706.08359).” arXiv:1706.08359, 2017.