# 【學習人工智能】線型回歸和sigmoid回歸(附實戰)
程序猿
**深度學習篇:線型回歸和sigmoid回歸**
**本篇難度系數:2星**
本來想給這篇文章寫個難度1星,但聯想到本人較為弱勢的數學,姑且還是給個2星吧。sigmoid回歸是logistic回歸的一種,而logistic regression和線型回歸也是近親,本質都是一個東西。那么說回歸回歸,回歸是個啥?
其實很好理解,通俗意義上講,線型回歸就是讓你找一條直線把兩種(或多種)類型的標簽分為兩類(或多種),**而sigmoid回歸就是讓你找一條直線,把經過sigmoid化后的輸入數據與模型的乘積分成兩類。**
有同學立刻問,什么是sigmoid,為什么要用sigmoid。
這個問題要從sigmoid是什么開始說起。
sigmoid函數并不難,就是這么個東西。
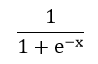
**注意,x可以是數,可以是向量,sigmoid一個向量的意思,就是分別對期中的每一個元素做sigmoid。**那么為什么要搞這么個東西。因為這個東西長這樣。
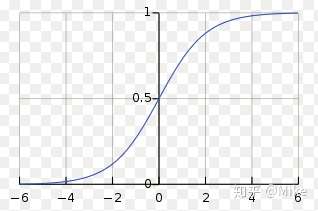
比如你的x>8,那么,那么sigmoid可以基本上把它歸為1類,但是如果你的函數是y=x,這個label也就是y可就是8了,這是很不方便的。有同學又說,為什么不搞個符號函數,
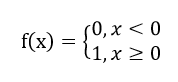
這是好問題,答案是,很難求導。又有人問,為什么要求導?我們不用急,接著往下看。
sigmoid回歸問題最重要的幾個公式:
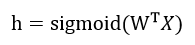
這個好理解,就是一個簡單的矩陣相乘公式。這個h是在算概率呢。
那么出現 label = 1的標簽的時候,其概率為h,出現 label = 0 的標簽的時候,其概率為 1-h,即:
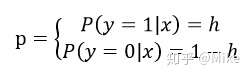
因此我們可以得到綜合概率函數:
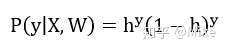
由這個綜合概率函數,我們可以得到似然函數
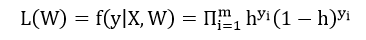
這個東西簡單,這個東西不就是你把所有的樣本給乘起來,我們默認這些樣本是獨立同分布的。共有m個樣本。
下面搞了個對數,為的是化簡的時候能把累加乘 (\\Pi) 改成累加加 (\\sum)
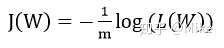
然后對這個東西去求導,原諒我實在不想一步一步地去求導了,我直接貼別人的公式了。
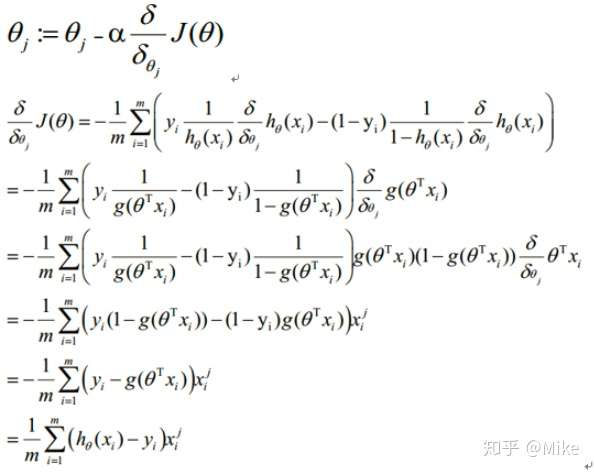
請注意,上面的theta就是我自己公式里面的W,這是一個東西。**這里應該有一個問題,那就是我們為什么要對 J 去求導,我們可以基本上認為,J就代表那個似然函數,我們當然希望我們的模型可以盡最大的可能性去往 J 上去貼,換句話說,我們希望我們的模型盡可能的準,也就是求最大值,而導數可以幫我們逐步地找到這個最大值。**
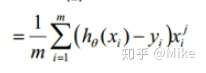
這個公式是元素的形式,對我們來說還是太復雜了,我們把它轉化一下。
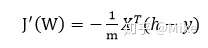
于是,更新公式為:
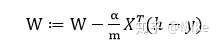
**對于編程來說,我們需要這個就夠了。**
**(1)one hot**
首先我們寫一個 make one hot 函數:
~~~text
def make_one_hot(data1, out):
return (np.arange(out)==data1[:,None]).astype(np.integer)
~~~
這個函數有什么用?比如說你的輸入是 y = \[1,0,1\].T
他會給你轉變成:
~~~text
[[0 1]
[1 0]
[0 1]]
~~~
沒看出規律我們再來一個:
y = \[1,2,4,0\].T
他會給你轉變成:
\[\[0 1 0 0 0\]
\[0 0 1 0 0\]
\[0 0 0 0 1\]
\[1 0 0 0 0\]\]
這回應該看出規律了吧。
**(2) sigmoid**
~~~python3
def sigmoid( x):
return 1.0/(1+np.exp(-x))
~~~
沒什么可說的。
**(3) logistic regression**
~~~python3
def logisticRegression(x, y):
m,n = np.shape(x)
alpha = 0.001
maxCycles = 5000
w = np.ones((n,2))
for k in range(maxCycles):
h = sigmoid(x.dot(w))
error = (h - y)
w = w - alpha * x.transpose().dot(error)
return w
~~~
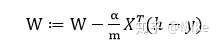
**請注意這句話(數學公式)在代碼中哪一個位置出現**。編程是容易的,因為我們僅僅使用數學推導的結論就可以了。注意:m是常數,我們直接用\\alpha 去替代 \\alpha/m, 這是沒有問題的。
**(4)準確率檢測**
~~~text
def acc(xs,ys,w):
p = sigmoid(xs.dot(w))
p = np.argmax(p,1)
s = 0
for i in range(len(p)):
if p[i] == np.argmax(ys[i]):
s += 1
return s/len(p)
~~~
也沒什么可以說的,就是比對吻合的樣本除以總數的百分比。
總結一下,其實logistic regression最核心的東西就是對**極大似然**和**梯度下降**的這兩個東西的運用。**而極大似然的本質就是根據樣本也就是x的分布規律虛擬出一個模型出來**。(這個模型是現實中不存在的,但是人們認為這個模型存在所以使得樣本符合某種規律),然后我們又通過 **梯度下降** 的方法不斷地微調我們的模型 W 能夠使得似然概率盡可能的大,而且似然函數我是存在一個極大值點的,也就是我們輸出的logit能盡可能的吻合真正的label。當梯度下降過程收斂的時候,我們的模型達到了最優的情況,從而達到有效分類的目的,這就是邏輯回歸的本質。
**另外:那些注重學術探討的人,懂得就事論事的人是朋友,是會受到歡迎的人;那些自己什么有價值的東西都說不出來,在一旁指點江山的人是渣滓,是會被社會淘汰的**
