? [TOC] # 什么是大O符號? **大O符號**（英語：Big O notation），又稱為**漸進符號**，是用于描述[函數](https://zh.wikipedia.org/wiki/%E5%87%BD%E6%95%B0 "函數")[漸近行為](https://zh.wikipedia.org/wiki/%E6%B8%90%E8%BF%91%E5%88%86%E6%9E%90 "漸近分析")的[數學](https://zh.wikipedia.org/wiki/%E6%95%B0%E5%AD%A6 "數學")符號。更確切地說，它是用另一個（通常更簡單的）函數來描述一個函數[數量級](https://zh.wikipedia.org/wiki/%E6%95%B0%E9%87%8F%E7%BA%A7 "數量級")的**漸近上界**。在[數學](https://zh.wikipedia.org/wiki/%E6%95%B0%E5%AD%A6 "數學")中，它一般用來刻畫被截斷的[無窮級數](https://zh.wikipedia.org/wiki/%E6%97%A0%E7%A9%B7%E7%BA%A7%E6%95%B0 "無窮級數")尤其是[漸近級數](https://zh.wikipedia.org/w/index.php?title=%E6%B8%90%E8%BF%91%E7%BA%A7%E6%95%B0&action=edit&redlink=1 "漸近級數（頁面不存在）")的剩余項；在[計算機科學](https://zh.wikipedia.org/wiki/%E8%AE%A1%E7%AE%97%E6%9C%BA%E7%A7%91%E5%AD%A6 "計算機科學")中，它在[分析](https://zh.wikipedia.org/wiki/%E7%AE%97%E6%B3%95%E5%88%86%E6%9E%90 "算法分析")[算法](https://zh.wikipedia.org/wiki/%E7%AE%97%E6%B3%95 "算法")[復雜性](https://zh.wikipedia.org/wiki/%E8%A8%88%E7%AE%97%E8%A4%87%E9%9B%9C%E6%80%A7%E7%90%86%E8%AB%96 "計算復雜性理論")的方面非常有用。 大O符號/大 O 表示法 只是描述代碼的性能如何取決于其處理的數據量的一種奇特的方式。 它允許我們計算一個算法可能的最壞運行時間，或者算法完成需要多長時間。 換句話說，它根據輸入的大小告訴我們它會慢多少。 ~~~ T(n) = O(f(n)) S(n) = O(f(n)) ~~~ 這個叫做大 O 表示法，其中的 T 代表的是算法需要執行的總時間 * S 表示的算法需要的總空間 * f (n) 表示的是代碼執行的總次數 它通常以兩種方式來討論**時間復雜度（Time Complexity）**(算法花費的時間)和**空間復雜度（Space Complexity）**(算法占用的空間)。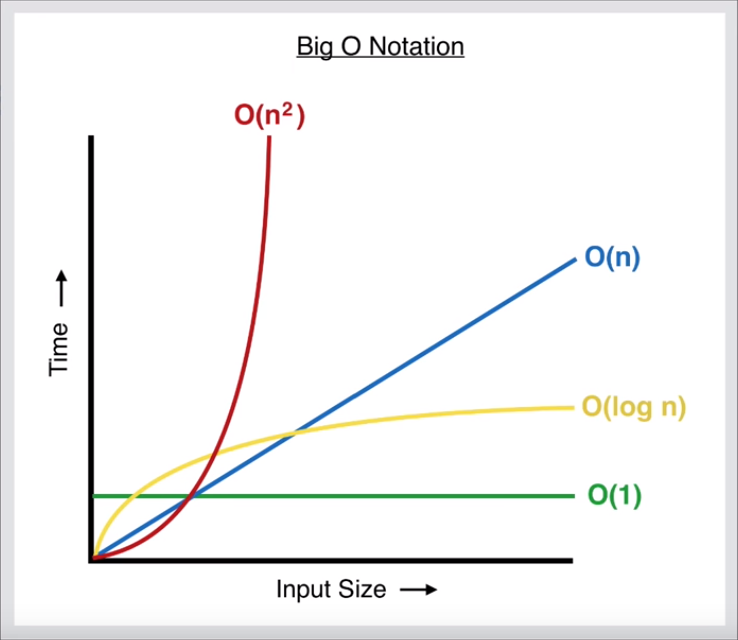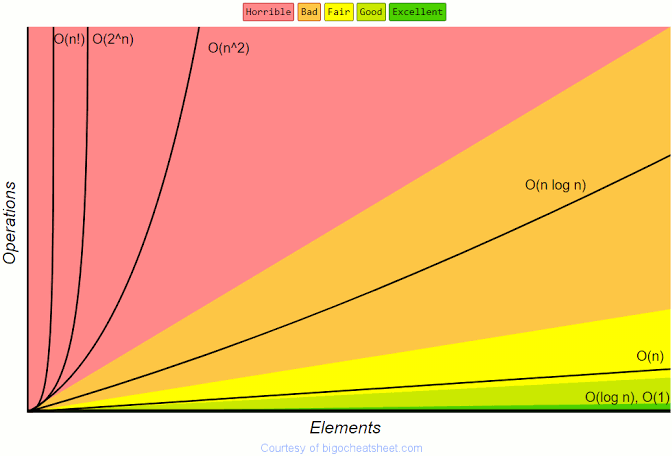 我把這個圖放在這里，我們繼續討論時可以參考它，這張圖顯示了相互之間的復雜性。   # 時間復雜度 首先什么是時間復雜度，時間復雜度這個定義如果在之前沒有接觸過的話，你可能會認為他代表的是一個代碼執行的時間，其實不然，算法的時間復雜度就是說一個算法的執行時間根據數據規模增長的一個趨勢，并不是說代碼執行的具體時間。 | 記號法| 名稱 | 表情符號| 簡短說明 | 詳細的描述 | | --- | --- |--- |--- |--- |--- | | O(1) | 常量 | ?? | 數據集的大小不影響運行速度 | 總是耗費相同的時間 | | O(log n) | 對數 | ?? | 10x the data means 2x more time | 每次循環迭代后的工作量除以2。如 二分查找|對分查找（binary search） | | O(n) | 線性 | ?? | 10x the data means 10x more time | 完成所需耗費的時間與輸入數據大小成 `1:1` 的關系。 | | O(n log n) | 直線的（linearithmic） | ?? | 10x the data means about 20x more time | 這是一個嵌套循環。其內部循環在 `log n` 時間內運行，例子包括快速排序（quicksort）、歸并排序（mergesort）和堆排序（heapsort） | | O(n2) | 二次方 | ?? | 10x the data take100x more time | 完成所需耗費的時間與 輸入數據大小以`^2` 的關系增長。當您有一個遍歷所有元素的循環時，該循環的每次迭代也會遍歷每個元素。這是一個嵌套循環！ | | O(2^n) | 指數 | ?? | —— | 完成所需耗費的時間與輸入大小的關系以 `2^` 增長。它比 `n^2` 慢多了，所以不要把它們混淆了！如遞歸斐波那契算法 | ## O(1) O（1）稱為恒定時間。具有常數的算法不會隨輸入大小縮放，無論輸入多大，它們都是恒定的。這里有幾個恒定的函數： ``` function value_at(arr, posn){ value = arr[posn] console.log("value:",value); } ``` 無論怎么樣，這段函數不受任何參數影響，代碼走一遍就完事，這種的代碼用 T (n) = O (1) 表示。 我們經常看到 O(1) 是常數，但是1用任何數都可以用，它仍然是常數。我們會把數字改成1，因為這與需要多少步無關。只是記錄它需要多少步完成。 ## O(log n) O（log n）稱為對數時間。為此，假設我們有一個包含**有序元素的數組**，并且我們試圖找到一個元素。那如何找到它？ 1. 遍歷所有元素，直到找到它。可行，但要花一點時間取決于元素。在 1 到 100 的元素數組中找到 1 是可以的，但是找到 65 則需要一段時間。 2. 二分查找|對分查找，通過重復地將數據集減半，直到找到目標值，來縮小查找范圍。 二分查找具有對數時間。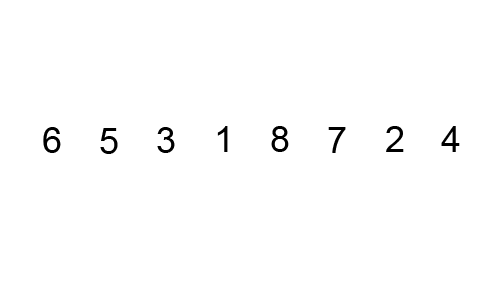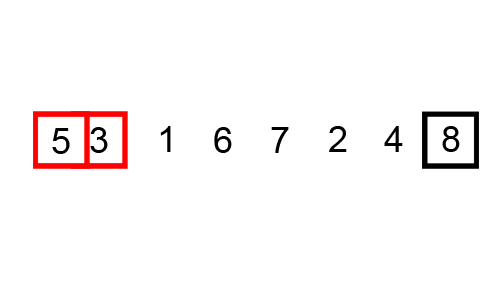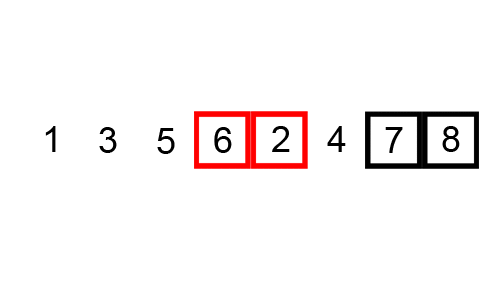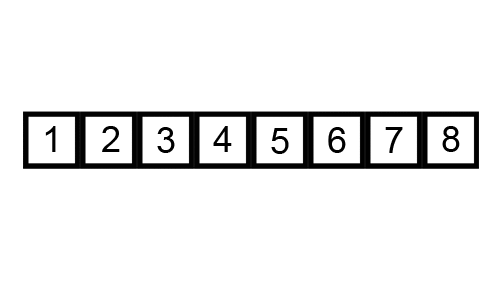 這是[二分查找](https://brilliant.org/wiki/binary-search/)圖：  二分查找代碼： ``` function binary_search(arr, item) { let first = 0; let last = arr.length - 1; while (first <= last) { // 相等情況 const midpoint = parseInt((first + last) / 2); // 下標取整 if (arr[midpoint] == item) { return true; // 找到直接返回 true } if (item < arr[midpoint]) { last = midpoint - 1; } else { first = midpoint + 1; } } return false; } ``` ## O(n) O(n) 被描述為線性時間。這意味著對于給定的算法，時間將隨著數據集大小的增加而增加。讓我們以一個數組為例，我們需要對它的項求和。大概是這樣的： ``` function sum_add(num_array) { const n = num_array.length; for (var i = 0; i < n; i++) { sum += i; } console.log("sum",sum); } ``` `sum_add` 簡單地接受一個數組，循環遍歷每個元素，然后添加所有內容，然后輸出 `sum`。 一個包含10個條目的數組肯定比一個包含 100 萬個條目的數組要快。通俗易懂，這段代碼的執行時間完全由 N 來控制，所以說 `T (n) = O (n)`。許多遍歷數組的代碼是 `O(n)`。 ## O(n log n) O(n log n) 是 linearithmic 時間。一個例子是歸并排序。如果我們有一個未排序的數組，我們希望它是按升序排列的。歸并排序將遞歸地將這個大數組分解成2個或更少元素的小數組，然后對這兩個元素排序，然后將它們合并，使元素按升序組織。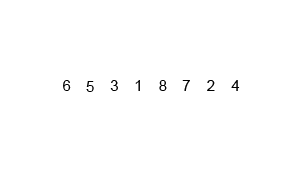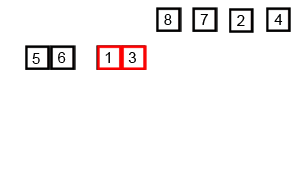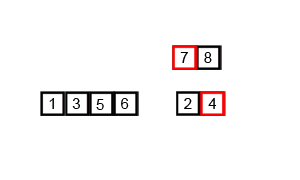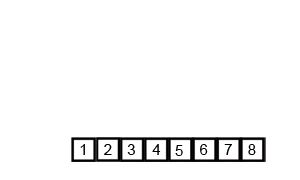 這圖展示了歸并排序的過程：  ``` def merge_sort(arr) return arr unless arr.size > 1 mid = arr.size/2 a, b, sorted = merge_sort(arr[0...mid]), merge_sort(arr[mid..-1]), [] sorted << (a[0] < b[0] ? a.shift : b.shift) while [a,b].none?(&:empty?) sorted + a + b end ``` ## O(n2) O(n2) 是二次的，這意味著 10倍的數據將花費 100倍的時間。我們剛剛看到 O(n) 被用在 for 循環中，這意味著你有另一個嵌套的 for 循環。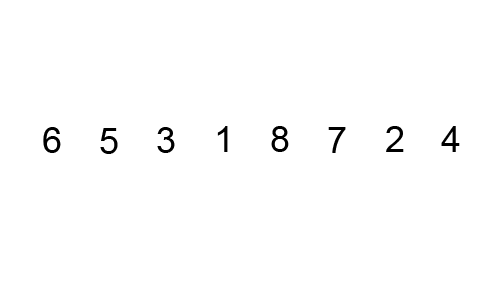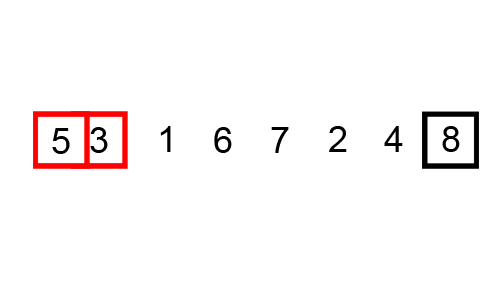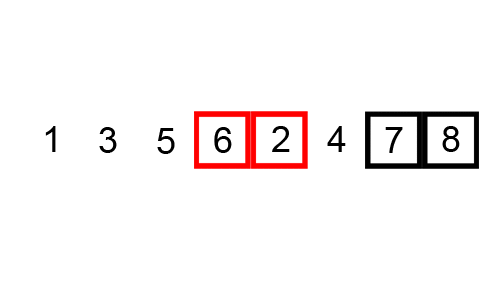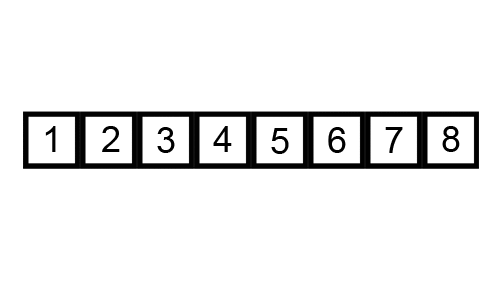 一個很好的例子是[冒泡排序](https://brilliant.org/wiki/bubble-sort)，這圖來展示冒泡排序：  ``` def bubble_sort(arr) n=arr.length for i in 0...n-1 for j in 0...n-i-1 if arr[j]>arr[j+1] temp=arr[j] arr[j]=arr[j+1] arr[j+1]=temp end end end return arr end ``` 嵌套循環： ~~~ function go(i) { var sum = 0; for (var j = 0; j < i; j++) { sum += i; } return sum; } function main(n) { var res = 0; for (var i = 0; i < n; i++) { res = res + go(i); // 這里是重點 } } ~~~ 在上邊的代碼種第二段代碼里邊調用了第一段代碼，所以說在這個代碼里邊是 ``` go:(1+n) ``` 在 `main` 函數里邊的時候是`(1+n*go)=(1+n+n*n)` 所以最后的時間復雜度是 `T (n) = O (n2)` 這也意味著在一個`for`循環中嵌套的次數越多，對 n 的冪就越大，一個嵌套了2 個 for 循環的 `for` 循環會給出(3個 for 循環)`O(n3)`， 3個嵌套的`for`循環會給出 `O(n?)`，等等！所以在嵌套 for 循環時要非常小心！ ## O(2^n) 這是指數函數，也是最慢的。指數時間的一個例子是找到一個集合的所有子集。 讓我們假設我們有一個叫做 `subsets` 的函數，該函數采用一個數組作為參數，并返回所有可能的子集。目的是采用數組并創建不同的值集。 ``` def subset(a) arr = [] for i in 0..(a.length) do arr = arr + a.combination(i).to_a end arr end ``` ``` >>> subsets(['']) [''] # 1 >>> subsets(['a']) ['', 'a'] # 2 >>> subsets(['a', 'b']) ['', 'a', 'ab', 'b'] # 4 >>> subsets('a', 'b', 'c']) ['', 'a', 'b', 'c', 'ab', 'ac', 'bc', 'abc'] # 8 ``` 當數組(a)有2個元素時我們有4個元素的輸出，這是 22，當輸入有3個元素時我們有8個元素的輸出，23。 輸出呈指數增長。 ## 如何計算時間復雜度 我們將利用現有的知識來嘗試找出每種情況的復雜性。記住，我們需要考慮最壞的情況。 ### 例1 舉個例子 ~~~ function go(n) { var item = 0; // 這里執行了一次 for (var i = 0; i < n; i++) { //這里執行了N次 for (var j = 0; j < n; j++) { //這里執行了n*n次 item = item + i + j; //這里執行了n*n次 } } return item; //這里執行了一次 } ~~~ 所以說上邊這段代碼是**1+n+n\*n\*2+1=2+n+2n2** 也就是說 `T (n) = O (f (2+n+2n2))` 然后之前說了時間復雜度看的是一個代碼執行的時間的趨勢， 所以說在 N，也就是規模比較大的時候，那些常量是起不到決定性的作用的，所以這個時候我們忽略這些常量，這里的例子是一個單段的代碼，這里只看最大量級的循環就可以了 所以最后的這個代碼的時間復雜度是 `T (n) = O (n2)` ### 例2 我們有一個電影列表，每部電影都有一個評級。我們希望找到一部電影，然后使用該電影的評級來查找其他具有類似評級的電影。 我們可以使用二分查找`O(log n)`來找到電影因為這樣更快，但這只是我們需要找到其他電影的一部分，我們還需要再次遍歷這個列表會用到我們的序列函數 `O(n)`，總的來說：`O(n log n)`還不錯。 我們現在可以在更高的層次上嘗試找出我們的算法，現在我們知道了： * halving（對分）=> O(log n) * for loops（for 循環）=> O(n) * nested for loops（嵌套的 for 循環） => O(n2) … 為了更好地理解如何計算時間復雜度，這里有一些鏈接： \- With [discrete maths](https://skerritt.blog/big-o/#-how-to-calculate-big-o-notation-of-a-function-discrete-maths-) \- Some [exercises with solutions](https://github.com/sf-wdi-31/algorithm-complexity-and-big-o) # 空間復雜度 空間復雜度是一個算法 / 程序使用的內存空間的總量的趨勢，包括用于執行的輸入值的空間。 空間復雜性常常與輔助空間混淆（*auxiliary space*）。輔助空間是算法使用的臨時或額外空間。 簡而言之： ``` 空間復雜度 = 輔助空間 + 輸入值使用的空間 ``` 空間復雜度使用與時間復雜度相同的符號法： O(n)、O(1) 等等。 讓我們看看這個使用ruby的簡單函數，并嘗試找出它的空間復雜度 ``` def sum array = [1,2,3] sum = 0 array.each {|i| sum = sum + i} puts sum end sum ``` 在 sum 函數中，我們有一個由 3 個元素組成的數組，我們循環遍歷這些元素，并在執行過程中將它們相加，完成后，我們打印出這些元素的和。 現在要算出它的空間復雜度，在我們深入之前知道整數的空間復雜度是 O(1) 是很重要的。因此，看看這個函數，我們有一個數組和兩個整數（sum, i）。 一個數組可以有任意數量的元素，n。數組占用的空間是 `4*n`個字節。假設每個整數占用 4 個字節，我們的整數占用 8 個字節。總空間是 `4n + 8`。消去常數，得到4n。函數的空間復雜度是 O(n) 線性復雜度。 # 小結 這里是一個[大O備忘單](https://www.bigocheatsheet.com/)，顯示了不同數據結構和數組排序算法的不同空間和時間復雜性。 # 參考 [https://github.com/trekhleb/javascript-algorithms](https://github.com/trekhleb/javascript-algorithms) [JavaScript 算法](https://juejin.im/post/5c9a1d58e51d4559bb5c6694) [JavaScript 算法之復雜度分析](https://juejin.im/post/5c2a1d9d6fb9a04a0f654581#heading-8) [從 js 講解時間復雜度和空間復雜度](https://www.ucloud.cn/yun/106364.html) [Data Structures with JavaScript](https://www.codeproject.com/Articles/669131/Data-Structures-with-JavaScript) [JavaScript 算法與數據結構](https://github.com/trekhleb/javascript-algorithms/blob/master/README.zh-CN.md) [Big O Notation — Time & Space Complexity in Ruby!](https://medium.com/@mendozabridget777/big-o-notation-time-space-complexity-9bc31952052c) [Bigocheatsheet](http://bigocheatsheet.com/) 介紹了計算機科學中常用算法的時空Big-O復雜性