## 以太坊默克爾壓縮前綴樹 在以太坊中，一種經過改良的默克爾樹非常關鍵，是以太坊數據安全與效率的保障，此樹在以太坊中稱之為 MPT（默克爾壓縮前綴樹）。 MPT 全稱是 Merkle Patricia Trie 也叫 Merkle Patricia Tree，是 Merkle Tree 和 Patricia Tree 的混合物。 Merkle Tree(默克爾樹) 用于保證數據安全，Patricia Tree(基數樹,也叫基數特里樹或壓縮前綴樹) 用于提升樹的讀寫效率。 ### 簡述 以太坊不同于比特幣的 UXTO 模型，在賬戶存在多個屬性（余額、代碼、存儲信息），屬性（狀態）需要經常更新。因此需要一種數據結構來滿足幾點要求： * ①在執行插入、修改或者刪除操作后能快速計算新的樹根，而無需重新計算整個樹。 * ②即使攻擊者故意構造非常深的樹，它的深度也是有限的。否則，攻擊者可以通過特意構建足夠深的樹使得每次樹更新變得極慢，從而執行拒絕服務攻擊。 * ③樹的根值僅取決于數據，而不取決于更新的順序。以不同的順序更新，甚至是從頭重新計算樹都不會改變樹的根值。 要求①是默克爾樹特性，但要求②③則非默克爾樹的優勢。 對于要求②，可將數據 Key 進行一次哈希計算，得到確定長度的哈希值參與樹的構建。而要求③則是引入位置確定的壓縮前綴樹并加以改進。 ### 壓縮前綴樹 Patricia Tree 在[壓縮前綴樹（基數樹）中，鍵值是通過樹到達相應值的實際路徑值。 也就是說，從樹的根節點開始，鍵中的每個字符會告訴您要遵循哪個子節點以獲取相應的值，其中值存儲在葉節點中，葉節點終止了穿過樹的每個路徑。假設鍵是包含 N 個字符的字母，則樹中的每個節點最多可以有 N 個子級，并且樹的最大深度是鍵的最大長度。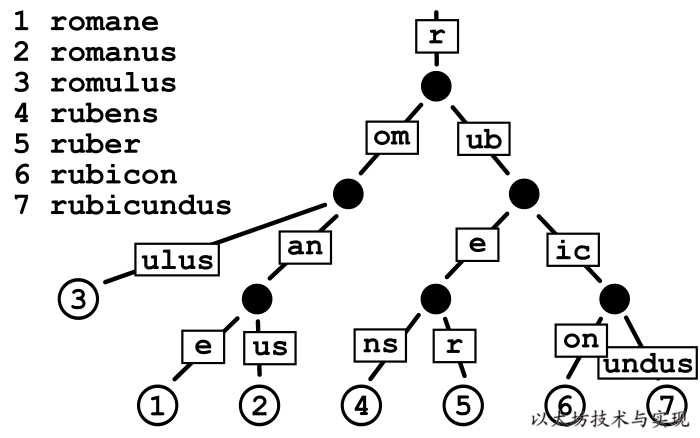  雖然基數樹使得以相同字符序列開頭的鍵的值在樹中靠得更近，但是它們可能效率很低。 例如，當你有一個超長鍵且沒有其他鍵與之共享前綴時，即使路徑上沒有其他值，但你必須在樹中移動（并存儲）大量節點才能獲得該值。 這種低效在以太坊中會更加明顯，因為參與樹構建的 Key 是一個哈希值有 64 長（32 字節），則樹的最長深度是 64。樹中每個節點必須存儲 32 字節，一個 Key 就需要至少 2KB 來存儲，其中包含大量空白內容。 因此，在經常需要更新的以太坊狀態樹中，優化改進基數樹，以提高效率、降低樹的深度和減少 IO 次數，是必要的。 ### 以太坊壓縮前綴樹（MPT） 為了解決基數樹的效率問題，以太坊對基數樹的最大改動是豐富了節點類型，圍繞不同節點類型的不同操作來解決效率。 1. 空白節點 NULL 2. 分支節點 branch Node [0,1,…,16,value] 3. 葉子節點 leaf Node : [key,value] 4. 擴展節點 extension Node: [key,value] 多種節點類型的不同操作方式，雖然提升了效率，但復雜度被加大。而在 geth 中，為了適應實現，節點類型的設計稍有不同： ~~~go //trie/node.go:35 type ( fullNode struct { //分支節點 Children [17]node flags nodeFlag } shortNode struct { //短節點：葉子節點、擴展節點 Key []byte Val node flags nodeFlag } hashNode []byte //哈希節點 valueNode []byte //數據節點,但他的值就是實際的數據值 ) var nilValueNode = valueNode(nil) //空白節點 ~~~ * fullNode: 分支節點，fullNode\[16\]的類型是 valueNode。前 16 個元素對應鍵中可能存在的一個十六進制字符。如果鍵\[key,value\]在對應的分支處結束，則在列表末尾存儲 value 。 * shortNode: 葉子節點或者擴展節點，當 shortNode.Key的末尾字節是終止符`16`時表示為葉子節點。當 shortNode 是葉子節點是，Val 是 valueNode。 * hashNode: 應該取名為 collapsedNode 折疊節點更合適些，但因為其值是一個哈希值當做指針使用，所以取名 hashNode。使用這個哈希值可以從數據庫讀取節點數據展開節點。 * valueNode: 數據節點，實際的業務數據值，嚴格來說他不屬于樹中的節點，它只存在于 fullNode.Children 或者 shortNode.Val 中。 ### 各類key 在改進過程中，為適應不同場景應用，以太坊定義了幾種不同類型的 key 。 1. keybytes ：數據的原始 key 2. Secure Key: 是 Keccak256(keybytes) 結果，用于規避 key 深度攻擊，長度固定為 32 字節。 3. Hex Key: 將 Key 進行半字節拆解后的 key ，用于 MPT 的樹路徑中和降低子節點水平寬度。 4. HP Key: Hex 前綴編碼(hex prefix encoding)，在節點存持久化時，將對節點 key 進行壓縮編碼，并加入節點類型標簽，以便從存儲讀取節點數據后可分辨節點類型。 下圖是 key 有特定的使用場景，基本支持逆向編碼，在下面的講解中 Key 在不同語義下特指的類型有所不同。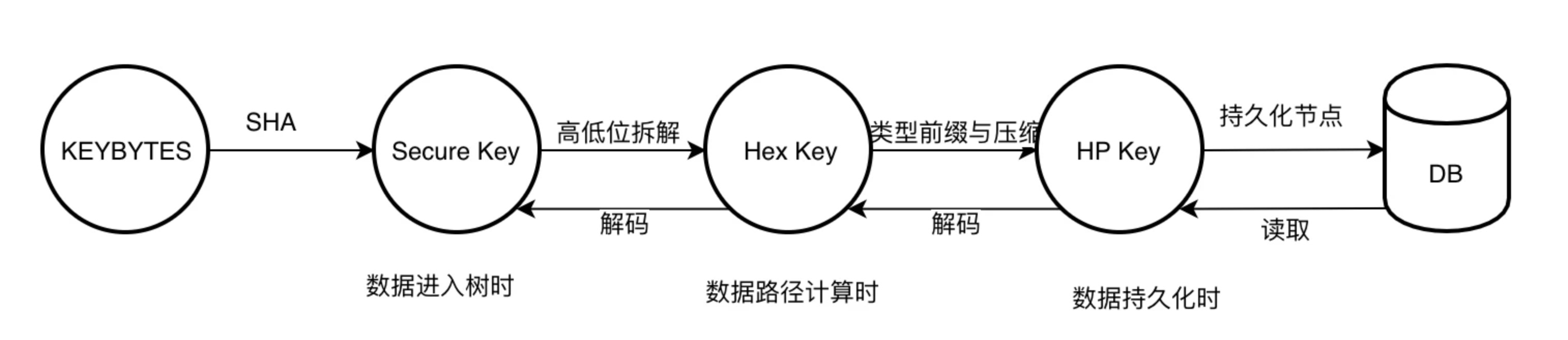  ### 分支節點 分支節點是以太坊引入，將其子節點直接包含在自身的數據插槽中，這樣可縮減樹深度和減少IO次數，特別是當插槽中均有子節點存在時，改進效果越明顯。 分支節點沒有key，可能value也為空。分支節點存儲多個子節點的hash。 數據 Key 在進入 MPT 前已轉換 Secure Key。 因此，key 長度為 32 字節，每個字節的值范圍是[0 - 255]。 如果在分支節點中使用 256 個插槽，空間開銷非常高，造成浪費，畢竟空插槽在持久化時也需要占用空間。同時超大容量的插槽，也會可能使得持久化數據過大，可能會造成讀取持久化數據時占用過多內存。 如果將 Key 進行Hex 編碼，每個字節值范圍被縮小到 [0-15] 內(4bits)。這樣，分支節點只需要 16 個插槽來存放子節點：  1. MPT 是一顆邏輯樹，并不一一對應物理樹（存儲）。 2. 在 MPT 中必將在葉子節點處存放在 Key 對應的數據節點（ValueNode），數據節點必然是在樹的子葉節點中。 3. 在 MPT 中，到達節點的樹路徑 Path 和節點中記錄的 Key 一起構成了節點的完整 Key。 4. 分支節點的插槽 Index 就是樹路徑的一部分。 ### 計算樹的Root 們以 romane、romanus、romulus 為示例數據，來講解是何如計算出 MPT 樹的一個樹根 Root 值的。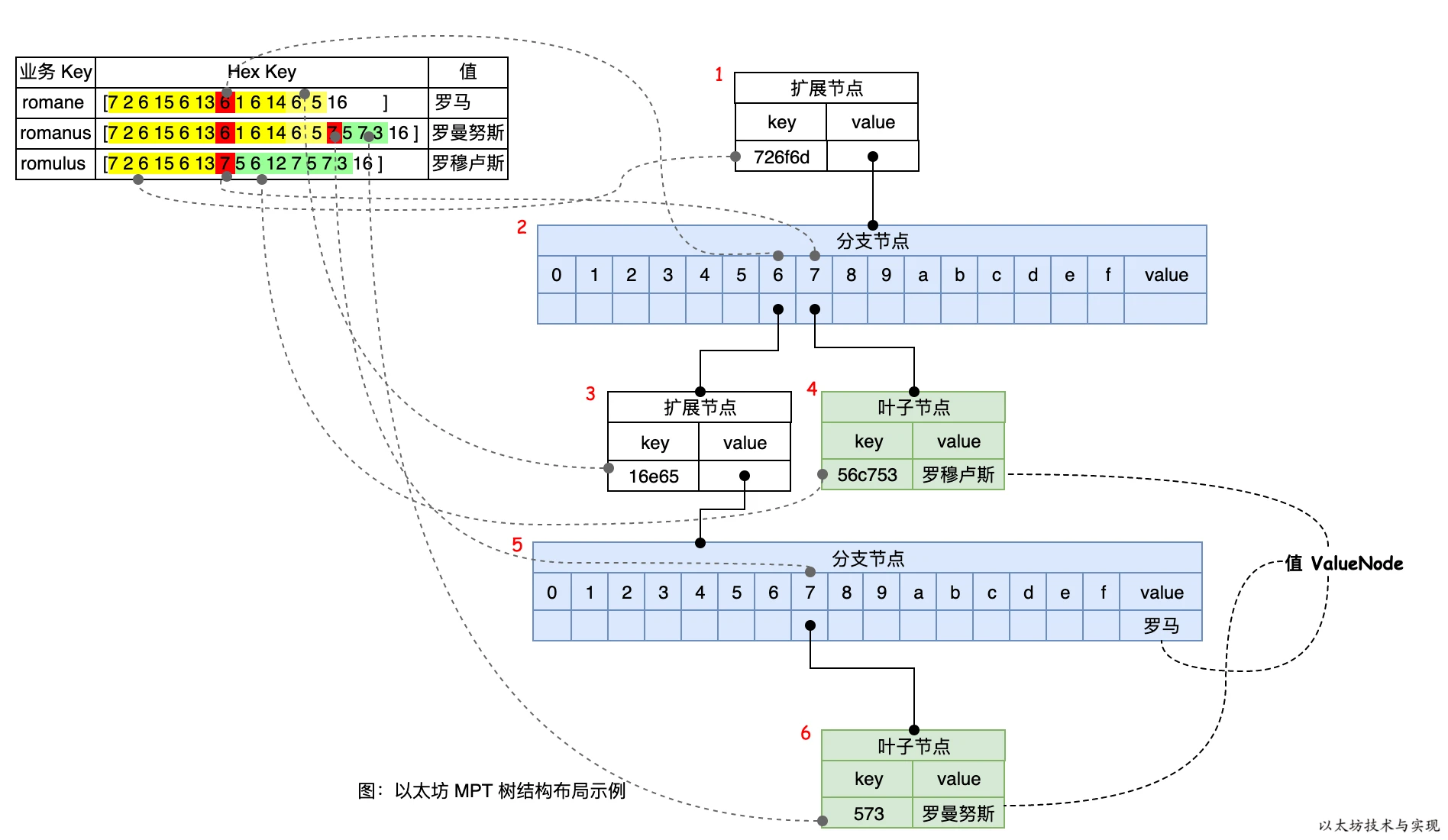  上圖是三項數據的業務 Key 經過 HP 編碼后，寫入 MPT 樹后所形成的 MPT 樹結構布局。HP表和樹的虛線連接表示樹路徑的生成依據，這是根據前面所描述的 MPT 生成規則而形成的樹結構。在樹中，一共有6 個節點，其中節點 1 和 3 為擴展節點，節點 2 和 5 為分支節點，節點 4 和 6 為葉子節點。可以看到在分支節點 5 中的 value 位置存放著業務 key “romane” 所對應的值“羅馬”，但業務 key “romanus”和“romulus” 則存放在獨立的葉子節點中。 當我們執行 trie.Commit 時將獲得一個 Hash 值，稱之為 樹的 Root 值，這個 Root 值是如何得到的呢？ Root 值算法源自默克爾樹（Merkle Tree），在默克爾樹中，樹根值是由從子葉開始不斷進行哈希計算得到最終能代表這棵樹數據的哈希值。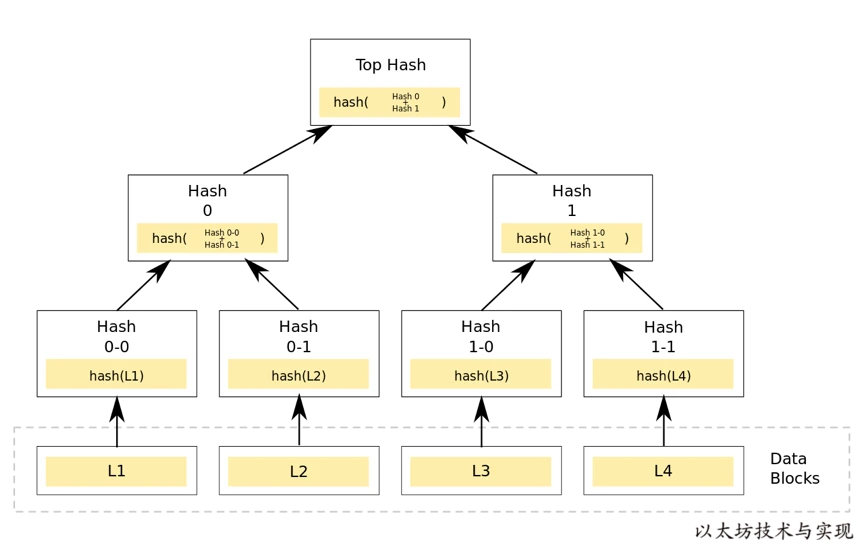  同樣在計算 MPT 樹的 Root 值是也是如此，在 MPT 中一個節點的哈希值，是節點內容經 RLP 編碼后的 Keccak256 哈希值。當對一個節點進行哈希計算遵循如下規則： 1. Hash(擴展節點)= Hash( HP(node.Key),Hash(node.Value) )， 節點 key 需 HP 編碼后參與哈希計算。當 node.Value 是表示業務數據時(valueNode)，將為 Hash( HP(node.Key),node.Value)。 2. Hash(葉子節點) 無，葉子節點只存在于分支節點中。 3. Hash(分支節點)= Hash( hash(node.Children[1\),…,hash(node.Children[i]),node.Value)，需要先將每個子節點存儲中的節點進行哈希。如果子節點為 null，則使用空字節表示。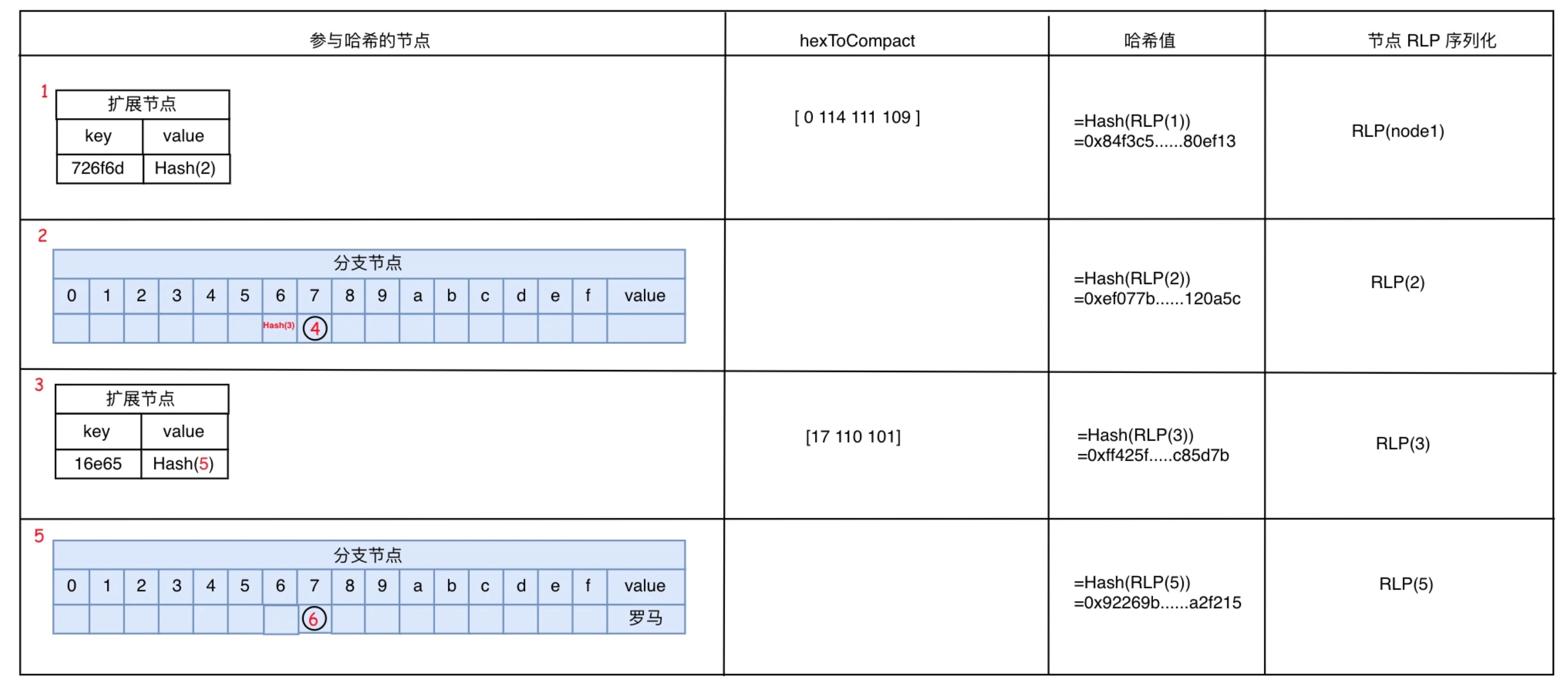 根據上面的規則，我們可以得到上面 MPT 樹進行哈希計算時的節點分布：  圖中，可哈希的節點只有 4 個，而葉子節點 4 和 6 則直接屬于分支節點的一部分參與哈希計算。MPT 的 Root 值是 MPT 樹根節點的哈希值。在本示例中，Root 節點為 節點 1，Hash(節點 1)=`0x84f3c5......80ef13`即為 MPT 的 Root 值。擴展節點 1 和 3 的 key 在哈希計算時有進行 HP 編碼。需要編碼的原因是為了區分擴展節點的 value 是葉子節點還是分支節點的區別。 ### 持久化 當需要將 MPT Commit 到 DB 時，這顆樹的數據是如何完整存儲到數據庫的呢？以太坊的持久層是 KV 數據庫，一個 Key 對應一份存儲內容。 當上面在計算 Root 值時，實際上已完成了哈希值和節點內容的處理過程。不同于在內存中計算 Root 值，在持久化時是持久化和 Hash 計算同步進行。 從Root的計算規則可知，HASH 計算是遞歸的，從樹的葉子節點向上計算。每次計算出一個節點哈希時，將使用此哈希值作為數據庫的 Key，存放節點的 RLP 持久化內容到數據庫中。 因為節點哈希值以及被包含在父節點中，直至樹根。因此，我們只需要知道一顆樹的 Root 值，便可以依次從 DB 中讀取節點數據，并在內存中構建完整的 MPT 樹。 ### 編碼規則 #### 1、Secure編碼 這并非 MPT 樹的必要部分，是為了解決路徑深度攻擊而將數據進入 MPT 前進行一次安全清洗，使用 Keccak256(key) 得到的key 的哈希值替換原數據 key。 在實現上，只需要在原 MPT 樹進行依次封裝即可獲得一顆 Secure MPT 樹。 #### 2、Hex編碼 用于樹路徑中，是將數據 key 進行半字節拆解而成。即依次將 key\[0\],key\[1\],…,key\[n\] 分別進行半字節拆分成兩個數，再依次存放在長度為 len(key)+1 的數組中。 并在數組末尾寫入終止符`16`。算法如下： > 半字節，在計算機中，通常將8位二進制數稱為字節，而把4位二進制數稱為半字節。 高四位和低四位，這里的“位”是針對二進制來說的。比如數字 250 的二進制數為 11111010，則高四位是左邊的 1111，低四位是右邊的 1010。 ~~~go // trie/encoding.go:65 func keybytesToHex(str []byte) []byte { l := len(str)*2 + 1 var nibbles = make([]byte, l) for i, b := range str { nibbles[i*2] = b / 16 nibbles[i*2+1] = b % 16 } nibbles[l-1] = 16 return nibbles } ~~~ 例如：字符串 “romane” 的 bytes 是`[114 111 109 97 110 101]`，在 HEX 編碼時將其依次處理： | i | key\[i\] | key\[i\]二進制 | nibbles\[i\*2\]=高四位 | nibbles\[i\*2+1\]=低四位 | | --- | --- | --- | --- | --- | | 0 | 114 | 011100102 | 01112\= 7 | 00102\= 2 | | 1 | 111 | 011011112 | 01102\=6 | 11112\=15 | | 2 | 109 | 011011012 | 01102\=6 | 11012\=13 | | 3 | 97 | 011000012 | 01102\=6 | 00012\=1 | | 4 | 110 | 011011102 | 01102\=6 | 11102\=14 | | 5 | 101 | 011001012 | 01102\=6 | 01012\=5 | 最終得到 Hex(“romane”) =`[7 2 6 15 6 13 6 1 6 14 6 5 16]` #### 3、HP(Hex-Prefix) 編碼 Hex-Prefix 編碼是一種任意量的半字節轉換為數組的有效方式，還可以在存入一個標識符來區分不同節點類型。 因此 HP 編碼是在由一個標識符前綴和半字節轉換為數組的兩部分組成。存入到數據庫中存在節點 Key 的只有擴展節點和葉子節點，因此 HP 只用于區分擴展節點和葉子節點，不涉及無節點 key 的分支節點。  前綴標識符由兩部分組成：節點類型和奇偶標識，并存儲在編碼后字節的第一個半字節中。 0 表示擴展節點類型，1 表示葉子節點，偶為 0，奇為 1。最終可以得到唯一標識的前綴標識： * 0：偶長度的擴展節點 * 1：奇長度的擴展節點 * 2：偶長度的葉子節點 * 3：奇長度的葉子節點 當偶長度時，第一個字節的低四位用`0`填充，當是奇長度時，則將 key\[0\] 存放在第一個字節的低四位中，這樣 HP 編碼結果始終是偶長度。 這里為什么要區分節點 key 長度的奇偶呢？這是因為，半字節`1`和`01`在轉換為 bytes 格式時都成為`<01>`，無法區分兩者。 例如，上圖 “以太坊 MPT 樹的哈希計算”中的控制節點1的key 為`[ 7 2 6 f 6 d]`，因為是偶長度，則 HP[0]= (00000000)2\=0，H[1:]= 解碼半字節(key)。 而節點 3 的 key 為`[1 6 e 6 5]`，為奇長度，則 HP[0]= (0001 0001)2\=17。 下面是 HP 編碼算法的 Go 語言實現： ~~~go // trie/encoding.go:37 func hexToCompact(hex []byte) []byte { terminator := byte(0) if hasTerm(hex) { terminator = 1 hex = hex[:len(hex)-1] } buf := make([]byte, len(hex)/2+1) buf[0] = terminator << 5 // the flag byte if len(hex)&1 == 1 { buf[0] |= 1 << 4 // odd flag buf[0] |= hex[0] // first nibble is contained in the first byte hex = hex[1:] } decodeNibbles(hex, buf[1:]) return buf } func decodeNibbles(nibbles []byte, bytes []byte) { for bi, ni := 0, 0; ni < len(nibbles); bi, ni = bi+1, ni+2 { bytes[bi] = nibbles[ni]<<4 | nibbles[ni+1] } } ~~~ 在 Go 語言中因為葉子節點的末尾字節必然是 16（Hex 編碼的終止符），依據此可以區分擴展節點還是葉子節點。