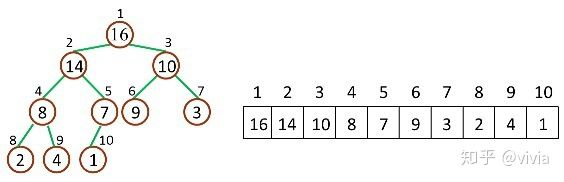
## **堆排序** 堆排序(Heapsort)是指利用堆積樹（堆）這種數據結構所設計的一種排序算法，它是選擇排序的一種。可以利用數組的特點快速定位指定索引的元素。堆排序就是把最大堆堆頂的最大數取出，將剩余的堆繼續調整為最大堆，再次將堆頂的最大數取出，這個過程持續到剩余數只有一個時結束。 ## **堆的概念** 堆是一種特殊的完全二叉樹（complete binary tree）。完全二叉樹的一個“優秀”的性質是，除了最底層之外，每一層都是滿的，這使得堆可以利用數組來表示（普通的一般的二叉樹通常用鏈表作為基本容器表示），每一個結點對應數組中的一個元素。 如下圖，是一個堆和數組的相互關系：  對于給定的某個結點的下標 i，可以很容易的計算出這個結點的父結點、孩子結點的下標： * Parent(i) = floor(i/2)，i 的父節點下標 * Left(i) = 2i，i 的左子節點下標 * Right(i) = 2i + 1，i 的右子節點下標 二叉堆一般分為兩種：最大堆和最小堆。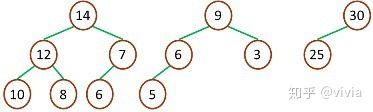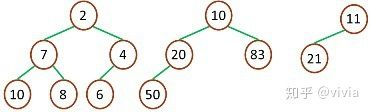 **最大堆：** 最大堆中的最大元素值出現在根結點（堆頂） 堆中每個父節點的元素值都大于等于其孩子結點（如果存在）  **最小堆：** 最小堆中的最小元素值出現在根結點（堆頂） 堆中每個父節點的元素值都小于等于其孩子結點（如果存在）  ## **堆排序原理** 堆排序就是把最大堆堆頂的最大數取出，將剩余的堆繼續調整為最大堆，再次將堆頂的最大數取出，這個過程持續到剩余數只有一個時結束。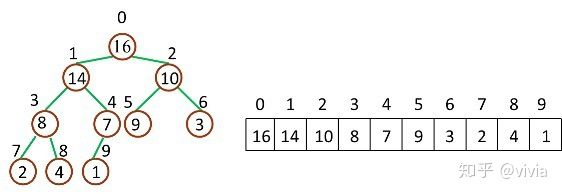在堆中定義以下幾種操作： * 最大堆調整（Max-Heapify）：將堆的末端子節點作調整，使得子節點永遠小于父節點 * 創建最大堆（Build-Max-Heap）：將堆所有數據重新排序，使其成為最大堆 * 堆排序（Heap-Sort）：移除位在第一個數據的根節點，并做最大堆調整的遞歸運算 繼續進行下面的討論前，需要注意的一個問題是：數組都是 Zero-Based，這就意味著我們的堆數據結構模型要發生改變  相應的，幾個計算公式也要作出相應調整： * Parent(i) = floor((i-1)/2)，i 的父節點下標 * Left(i) = 2i + 1，i 的左子節點下標 * Right(i) = 2(i + 1)，i 的右子節點下標 ## **堆的建立和維護** 堆可以支持多種操作，但現在我們關心的只有兩個問題： 1. 給定一個無序數組，如何建立為堆？ 2. 刪除堆頂元素后，如何調整數組成為新堆？ 先看第二個問題。假定我們已經有一個現成的大根堆。現在我們刪除了根元素，但并沒有移動別的元素。想想發生了什么：根元素空了，但其它元素還保持著堆的性質。我們可以把**最后一個元素**（代號A）移動到根元素的位置。如果不是特殊情況，則堆的性質被破壞。但這僅僅是由于A小于其某個子元素。于是，我們可以把A和這個子元素調換位置。如果A大于其所有子元素，則堆調整好了；否則，重復上述過程，A元素在樹形結構中不斷“下沉”，直到合適的位置，數組重新恢復堆的性質。上述過程一般稱為“篩選”，方向顯然是自上而下。 > 刪除后的調整，是把最后一個元素放到堆頂，自上而下比較 刪除一個元素是如此，插入一個新元素也是如此。不同的是，我們把新元素放在**末尾**，然后和其父節點做比較，即自下而上篩選。 > 插入是把新元素放在末尾，自下而上比較 那么，第一個問題怎么解決呢？ 常規方法是從第一個非葉子結點向下篩選，直到根元素篩選完畢。這個方法叫“篩選法”，需要循環篩選n/2個元素。 但我們還可以借鑒“插入排序”的思路。我們可以視第一個元素為一個堆，然后不斷向其中添加新元素。這個方法叫做“插入法”，需要循環插入(n-1)個元素。 由于篩選法和插入法的方式不同，所以，相同的數據，它們建立的堆一般不同。大致了解堆之后，堆排序就是水到渠成的事情了。 ## **算法描述** 我們需要一個升序的序列，怎么辦呢？我們可以建立一個最小堆，然后每次輸出根元素。但是，這個方法需要額外的空間（否則將造成大量的元素移動，其復雜度會飆升到O(n2) ）。如果我們需要就地排序（即不允許有O(n)空間復雜度），怎么辦？ 有辦法。我們可以建立最大堆，然后我們倒著輸出，在最后一個位置輸出最大值，次末位置輸出次大值……由于每次輸出的最大元素會騰出第一個空間，因此，我們恰好可以放置這樣的元素而不需要額外空間。很漂亮的想法，是不是？ ## **穩定性** 堆排序存在大量的篩選和移動過程，屬于不穩定的排序算法。 ## **適用場景** 堆排序在建立堆和調整堆的過程中會產生比較大的開銷，在元素少的時候并不適用。但是，在元素比較多的情況下，還是不錯的一個選擇。尤其是在解決諸如“前n大的數”一類問題時，幾乎是首選算法。 ## **JAVA代碼實現** ``` public class ArrayHeap { private int[] arr; public ArrayHeap(int[] arr) { this.arr = arr; } private int getParentIndex(int child) { return (child - 1) / 2; } private int getLeftChildIndex(int parent) { return 2 * parent + 1; } private void swap(int i, int j) { int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } /** * 調整堆。 */ private void adjustHeap(int i, int len) { int left, right, j; left = getLeftChildIndex(i); while (left <= len) { right = left + 1; j = left; if (j < len && arr[left] < arr[right]) { j++; } if (arr[i] < arr[j]) { swap(array, i, j); i = j; left = getLeftChildIndex(i); } else { break; // 停止篩選 } } } /** * 堆排序。 * */ public void sort() { int last = arr.length - 1; // 初始化最大堆 for (int i = getParentIndex(last); i >= 0; --i) { adjustHeap(i, last); } // 堆調整 while (last >= 0) { swap(0, last--); adjustHeap(0, last); } } } ```