# 幾種基本的數據結構
> 圖引自『我的第一本算法書』第一章
## 1.鏈表
### 概念圖
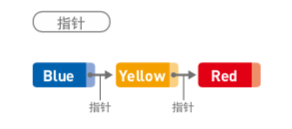
如下圖,`Blue`、`Yellow`、`Red`三個字符串存儲于鏈表中,每個數據都有一個『指針』,它指向下一個數據的內存地址(`Red`是最后一個數據,其指針不指向任何位置)。
### 在內存中存儲
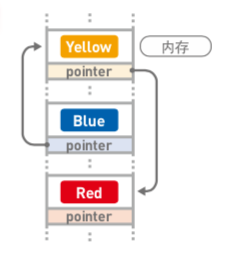
由上述內容可知,在鏈表中,數據無需存儲在連續空間內,一般都是分散存儲的。
### 訪問方式 - 順序訪問
因為數據是分散存儲的,所以想要訪問一個數據,只能從第一個數據開始,順著指針往下找。比如,想查找`Red`,查找順序如下:
`Blue` -> `Yellow` -> `Red`(Done)
查找數據的耗時和鏈表長度`n`有關,時間復雜度為:
O(n)
### 添加數據
如果想添加數據,只需改變添加位置前后的指針指向即可,比如『在`Blue`和`Yellow`直接添加`Green`』:
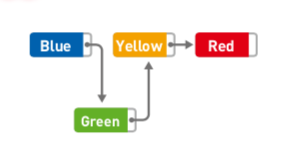
添加數據的耗時和鏈表長度`n`無關,如果已經到達需要添加數據的位置,則時間復雜度為:
O(1)
### 刪除數據
刪除數據也一樣,我們只需要改變指針的指向即可,比如『刪除`Yellow`』:
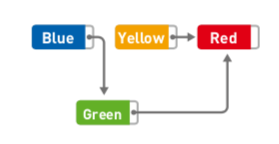
此時,`Yellow`本身還存在,不過沒關系,它已經無法被訪問,今后需要用到其所在存儲空間時,直接覆蓋掉即可。
和『添加數據』一樣,刪除數據的時間復雜度為:
O(1)
### 特點
由上述內容我們可以看出,鏈表有以下特點:
* 數據呈線性排列,分散存儲
* 訪問比較耗時 O(n)
* 數據的添加和刪除都比較方便 O(1)
## 2.數組
### 概念圖
數組也是線性排列的,它的結構和最開始講的『按姓名首字母排序的電話薄』類似。
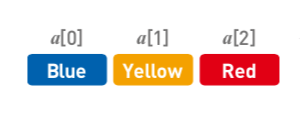
### 在內存中存儲
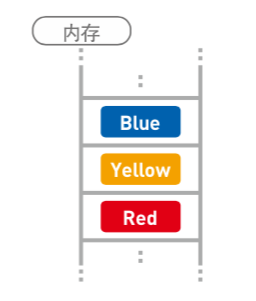
數組的數據按順序存放在連續空間內:
### 訪問方式 - 隨機訪問
因為數據存放在連續空間內,所以我們可以用數組下標計算出每個數據的內存位置,借此直接訪問目標數據,這叫做『隨機訪問』:
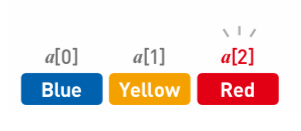
我們可以通過數組下標查找目標數據,查找數據的耗時和數組長度`n`無關,時間復雜度恒為:
O(n)
### 添加數據
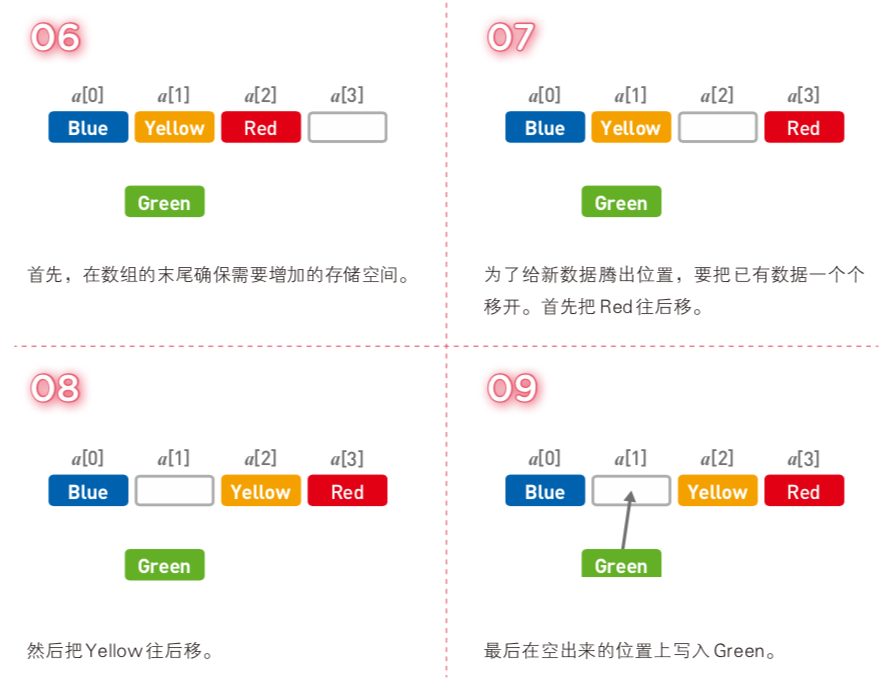
如果想添加數據,需要經過以下步驟:
① 在數組末位增加存儲空間
② 從新數據要存放的位置,把后面已有數據一個個后移
③ 插入新數據
例如,我們嘗試將`Green`添加到第二個位置上:
添加數據的耗時和鏈表長度`n`有關,如果在數組頭部添加數據,則時間復雜度為:
O(n)
### 刪除數據
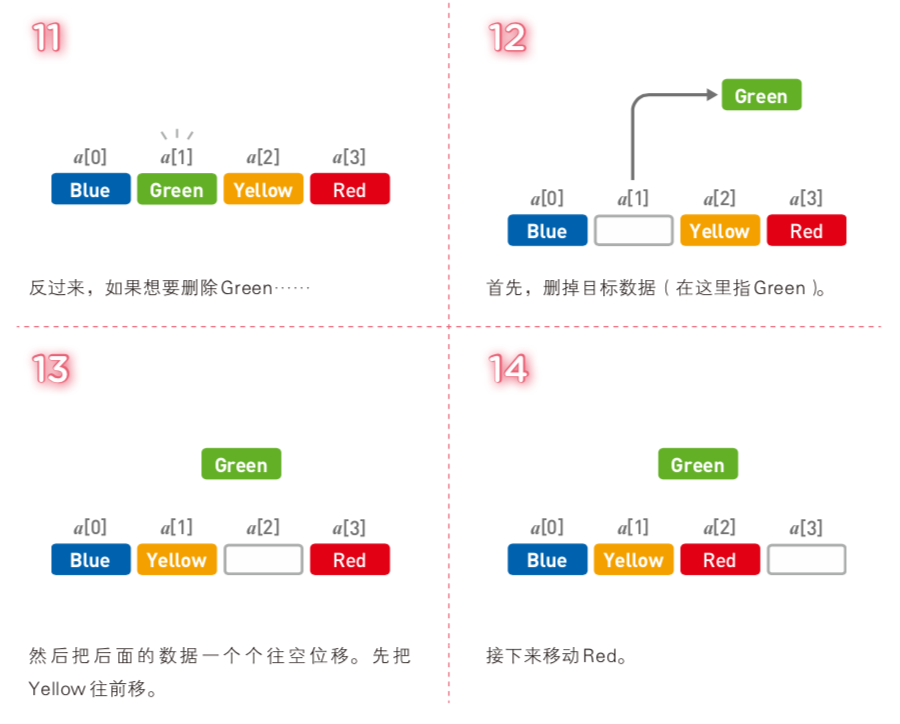
刪除數據是將『添加數據』反過來操作一遍,需要經過以下步驟:
① 刪除目標數據
② 把目標數據后面已有數據一個個往前移
③ 刪除末尾多余空間
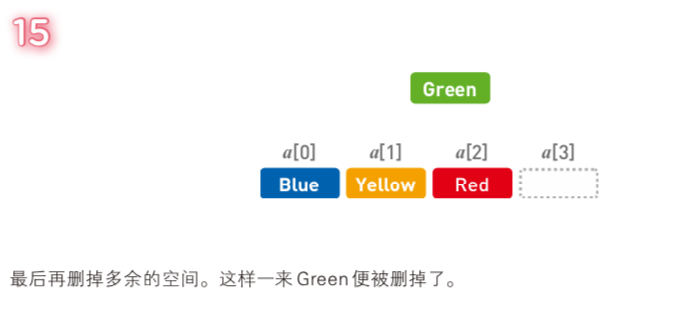
和『添加數據』一樣,刪除數據的時間復雜度為:
O(n)
### 特點
由上述內容我們可以看出,數組有以下特點:
* 數據呈線性排列,連續存儲
* 訪問快速 O(1)
* 數據的添加和刪除比較復雜 O(n)
### 和鏈表對比
通過對比,我們可以根據哪種操作頻繁來決定使用哪種數據結構。
|訪問|添加|刪除
---|---|---|
鏈表|慢|快|快
數組|快|慢|慢
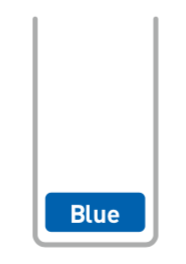
## 3.棧
### 概念圖
棧也是線性排列的。棧就像一摞書,新書都會被堆在最上面,取書時也只能從最上面開始取。
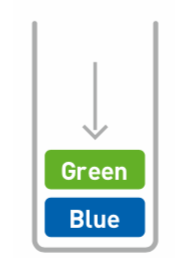
### 添加數據 - 入棧(`push`)
往棧中添加數據的操作叫做**入棧(`push`)**
添加`Green`:
添加`Red`:
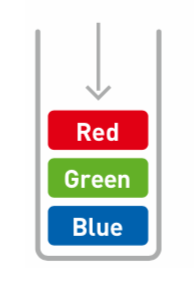
### 取出數據 - 出棧(`pop`)
從棧中取出數據的操作叫做**出棧**(`pop`)
例,我們要取出`Green`:
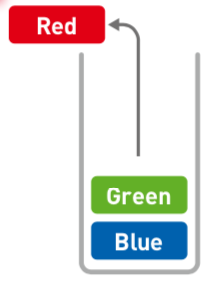
① 先取出`Red`:
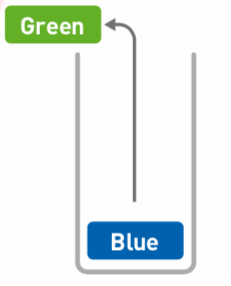
② 這時`Green`在頂部,才能通過出棧操作取出:
# 代碼庫地址
[https://github.com/liuzhen153/play-algorithm-python](https://github.com/liuzhen153/play-algorithm-python)
### 特點
由上述內容我們可以看出,棧有以下特點:
* 『后進先出』,Last In First Out (LIFO)
* 添加和刪除數據只能在一端進行
* 只能訪問到頂端的數據
* 要想訪問中間的數據,必須通過出棧操作將目標數據移到棧頂
* 很適合『只需要訪問最新數據』的情況
## 4.隊列
### 概念圖
隊列也是線性排列的。隊列就像排隊取款的人,只能從前面往后處理,新來的人只能排在隊尾。
### 添加數據 - 入列
往隊列中添加數據的操作叫做**入列**
添加`Green`:
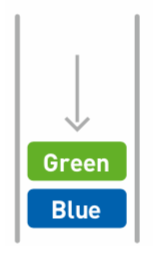
添加`Red`:
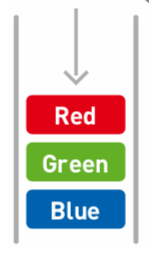
### 取出(刪除)數據 - 出列
從隊列中取出(刪除)數據的操作叫做**出列**
例,我們要取出`Green`:
① 先取出(刪除)`Blue`:
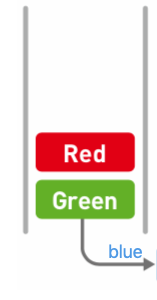
② 這時`Green`在頭部,才能通過出列操作取出(刪除):
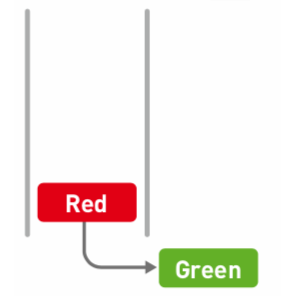
### 特點
由上述內容我們可以看出,隊列有以下特點:
* 『先進先出』,First In First Out (FIFO)
* 添加和刪除數據是在兩端進行的(添加-尾端,刪除-頭部)
* 只能訪問到頭部的數據
* 要想訪問中間的數據,必須通過出列操作將目標數據移到頭部
* 很適合『先來的數據先處理』的情況
