# [\[HDOJ 1003\]動態規劃法求和最大的連續子序列](https://www.cnblogs.com/ZhouYiJoe/p/12145611.html) 題目地址:?[http://acm.hdu.edu.cn/showproblem.php?pid=1003](http://acm.hdu.edu.cn/showproblem.php?pid=1003) Problem Description Given a sequence a\[1\],a\[2\],a\[3\]......a\[n\], your job is to calculate the max sum of a sub-sequence. For example, given (6,-1,5,4,-7), the max sum in this sequence is 6 + (-1) + 5 + 4 = 14. Input The first line of the input contains an integer T(1<=T<=20) which means the number of test cases. Then T lines follow, each line starts with a number N(1<=N<=100000), then N integers followed(all the integers are between -1000 and 1000). Output For each test case, you should output two lines. The first line is "Case #:", # means the number of the test case. The second line contains three integers, the Max Sum in the sequence, the start position of the sub-sequence, the end position of the sub-sequence. If there are more than one result, output the first one. Output a blank line between two cases. Sample Input 2 5 6 -1 5 4 -7 7 0 6 -1 1 -6 7 -5 Sample Output Case 1: 14 1 4 Case 2: 7 1 6 > 舉例：10 -1 -1 -1 -1 -10 -1 -1 -1 -1 -1 題目的大致意思就是要你從給定的數組中找出一段連續的子序列，使得這段連續的子序列中所有數字的總和不小于數組中其他任何一段連續子序列中數字的總和。只有傻子(我QAQ)才會用暴力枚舉的方法來做這題，必TLE。用分治法來做也是一種思路，不過我沒試過，不知道會不會TLE。最好的方法就是動態規劃。那么怎么做呢？ 動態規劃法其實在某種程度上也用的是枚舉的思路，只不過枚舉的方法比較巧妙而已。顯然，不論是哪一段連續子序列都是有終點的(廢話)，我們可以依次把數組中每一個元素都看作是連續子序列的終點，把以該元素為終點的所有連續子序列找出來。這樣就可以枚舉出數組中所有的連續子序列。 例如，有一個數組，它所包含的元素依次是5,9,2,4。以第一個元素為終點的連續子序列有"5"，以第二個元素為終點的連續子序列有"5,9","9"，以第三個元素為終點的連續子序列有"5,9,2","9,2","2"，以第四個元素為終點的連續子序列有"5,9,2,4","9,2,4","2,4","4"。于是以上找到的所有的連續子序列即為該數組中的所有連續子序列。 “講了半天，你這不還是暴力枚舉嘛......" 我們當然不是要以這種方式來暴力枚舉，而是要通過這樣一種思路，找到其中的遞推關系。既然現在我們是通過終點來尋找連續子序列的話，那么就定義一個函數dp(i):以數組中第i個元素作為終點，找出所有以第i個元素為終點的連續子序列，并依次求出這些連續子序列中所有元素的總和，所有總和中的最大值即為dp(i)的值。 例如，一個數組中的元素有1,-2,4,3。以第3個元素，也就是4，作為終點，找出所有以它為終點的連續子序列:"1,-2,4","-2,4","4"。序列"1,-2,4"的所有元素總和為3，序列"-2,4"的所有元素總和為2，序列"4”的所有元素總和為4。而4>3>2，則4為所有總和中的最大值，于是dp(3)=4。 相信你已經明白了這里定義的函數dp(i)的含義了。那么如何找到這個函數的遞推關系呢？ 說到遞推關系，首先當然要明確遞推的起點。顯然dp(1)的值就是數組中的第一個元素，這就是遞推的起點。接下來就只需要找到dp(i - 1)與dp(i)之間的關系，我們就可以求出dp(1),dp(2), ...... ,dp(i), ...... ,dp(n)了。很容易就可以知道，當dp(i - 1) >= 0時,dp(i) = dp(i - 1) + arr\[i\](arr\[i\]表示數組中第i個元素);當dp(i - 1) < 0時,dp(i) = arr\[i\]。 不過求出這些dp的值有什么用呢？剛才講過，依次以數組中每個元素為終點，找出以這些元素為終點的所有連續子序列，就能夠枚舉出數組的所有連續子序列。而求出所有dp值的過程其實就相當于把所有連續子序列都枚舉了一遍。既然已經找出了所有"局部"的最大值，那我們把這些"局部"的最大值合起來，找到"全局"的最大值，不就得到了問題的最終答案了嘛？所以，接下來我們要做的，就是從所有的dp值中，找出最大的那一個dp值，這個最大的dp值，就是元素總和最大的連續子序列。 終于把最關鍵的講完了，接下來放出代碼~這里先暫時只考慮求最大和的問題，所以只演示一個用來求最大和的函數，其他的后面再說。代碼可能寫得比較啰嗦，不過這是為了讓大家容易看得明白。 現在我們已經解決了如何求最大和的問題了，不過這道oj題還要求我們給出所求連續子序列的起點位置和終點位置。如果是用暴力枚舉法的話，很容易就可以記錄下起點位置和終點位置。不過如果是用動態規劃法的話，想要記錄下位置，可能還得稍微動一下腦子。不過也不難。我們自己手動模擬一下求dp值的過程，就可以找到其中的規律了。 下圖是計算一個數組的所有dp值的過程。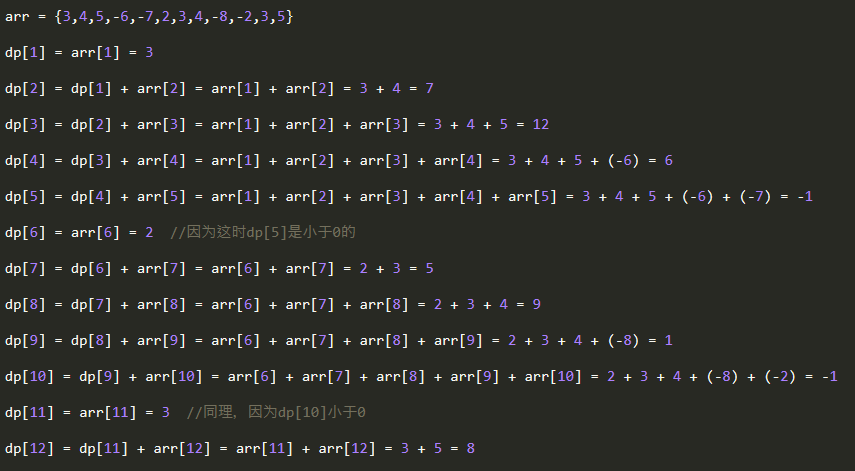 仔細觀察上圖，就可以找到其中的規律:計算一個數組的所有dp值的過程，其實是一個"從頭加到尾"的過程，只不過在dp值小于零的地方需要"斷開"。具體地說，計算一個數組的所有dp值時，我們需要做的是從第一個元素開始，依次取數，把這些數一個一個加起來。如果當加到第i個數時所得到的和為一個負數，則把前面i個數的和直接"丟掉"不要，然后從第i + 1個數開始，再從零開始加，之后循環往復地重復上述步驟。于是，我們就可以以這樣一種方法得到每個dp值對應的連續子序列的起點位置和終點位置:一開始把起點位置設為1，也就是整個數組的起點。顯然，dp(1)的終點位置也是1。然后求后面的dp值時，只要dp(i - 1)的值是非負的，那么dp(i)對應的起點位置就是dp(i - 1)的起點位置，而終點位置就是dp(i - 1)的終點位置 + 1。如果dp(i - 1)的值是負數，則dp(i)對應的起點位置就應該是i，終點位置也是i。