### 1.3 堆排序
堆結構:
算法中的堆結構指的是用數組實現的`完全二叉樹結構`,其模擬過程如下(數組元素從下標0開始):
~~~
?# 對于下標i的元素
?左孩子節點的下標為:2 * i + 1
?右孩子節點的下標為:2 * (i + 1)
?# 對于下標i的元素
?其父親節點的下標為:(i - 1) / 2
~~~
堆結構分為:
* 大根堆:每顆完全二叉樹都滿足最大元素在根節點。
* 小根堆:每顆完全二叉樹都滿足最小元素在根節點,Java中PriorityQueue優先級隊列結構就是小根堆結構。
與堆結構相關的有兩個關鍵的操作:
1. heapInsert():從最后一個元素開始調整堆結構,O(lgn)的時間復雜度。
2. heapify():從根元素往下調整堆結構,O(lgn)的時間復雜度。
代碼實現:
#### heapInsert
~~~
?/**
?* Adjust the heap from bottom to top.
?* @param arr
?* @param index
?*/
?private void heapInsert(int[] arr, int index) {
? ? ?while (arr[index] > arr[(index - 1) / 2]) {
? ? ? ? ?swap(arr, index, (index - 1) / 2);
? ? ? ? ?index = (index - 1) / 2;
? ? }
?}
~~~
#### heapify
~~~
?/**
?* Adjust the heap from root to bottom
?* @param arr
?* @param index
?* @param heapSize
?*/
?private void heapify(int[] arr, int index, int heapSize) {
? ? ?int left = 2 * index + 1;
? ? ?while (left < heapSize) {
? ? ? ? ?int largestIndex = (left + 1 < heapSize) && arr[left + 1] > arr[left] ? left + 1 : left;
? ? ? ? ?largestIndex = arr[largestIndex] > arr[index] ? largestIndex : index;
? ? ? ? ?if (largestIndex == index) {
? ? ? ? ? ? ?break;
? ? ? ? }
? ? ? ? ?swap(arr, largestIndex, index);
? ? ? ? ?index = largestIndex;
? ? ? ? ?left = 2 * index + 1;
? ? }
?}
~~~
該過程從根元素到葉子節點維護堆結構,只需每次判斷的時候找到左右節點的更大的一個值即可;heapify過程用在從堆中彈出一個元素的時候(根節點元素),用堆中的最后一個元素替換第一元素,然后再重新維護堆的過程。
#### heapSort
~~~
?/**
?* heap sort
?* @param arr
?*/
?public static void heapSort(int[] arr) {
? ? ?if (arr == null || arr.length < 2) {
? ? ? ? ?return;
? ? }
? ? ?// 維護根結構的的方式
? ? ?// for (int i = 0; i < arr.length; i++) {
? ? ?// ? ? heapInsert(arr, i);
? ? ?// }
? ? ?for (int i = arr.length - 1; i >= 0; i++) {
? ? ? ? ?heapify(arr, i, arr.length - 1);
? ? }
? ? ?int heapSize = arr.length;
? ? ?// 將最大值交換到堆結構的最后一個位置
? ? ?swap(arr, 0, --heapSize);
? ? ?while (heapSize > 0) {
? ? ? ? ?heapify(arr, 0, heapSize);
? ? ? ? ?swap(arr, 0, --heapSize);
? ? }
?}
~~~
整個堆排序的主要過程是逐個的將大根堆的根元素與堆的最后一個元素(用heapSize來指明)替換,然后再進行堆的維護,直到heapSize為0。
堆排序的時間復雜度為:O(nlgn)。
時間復雜度的推導:
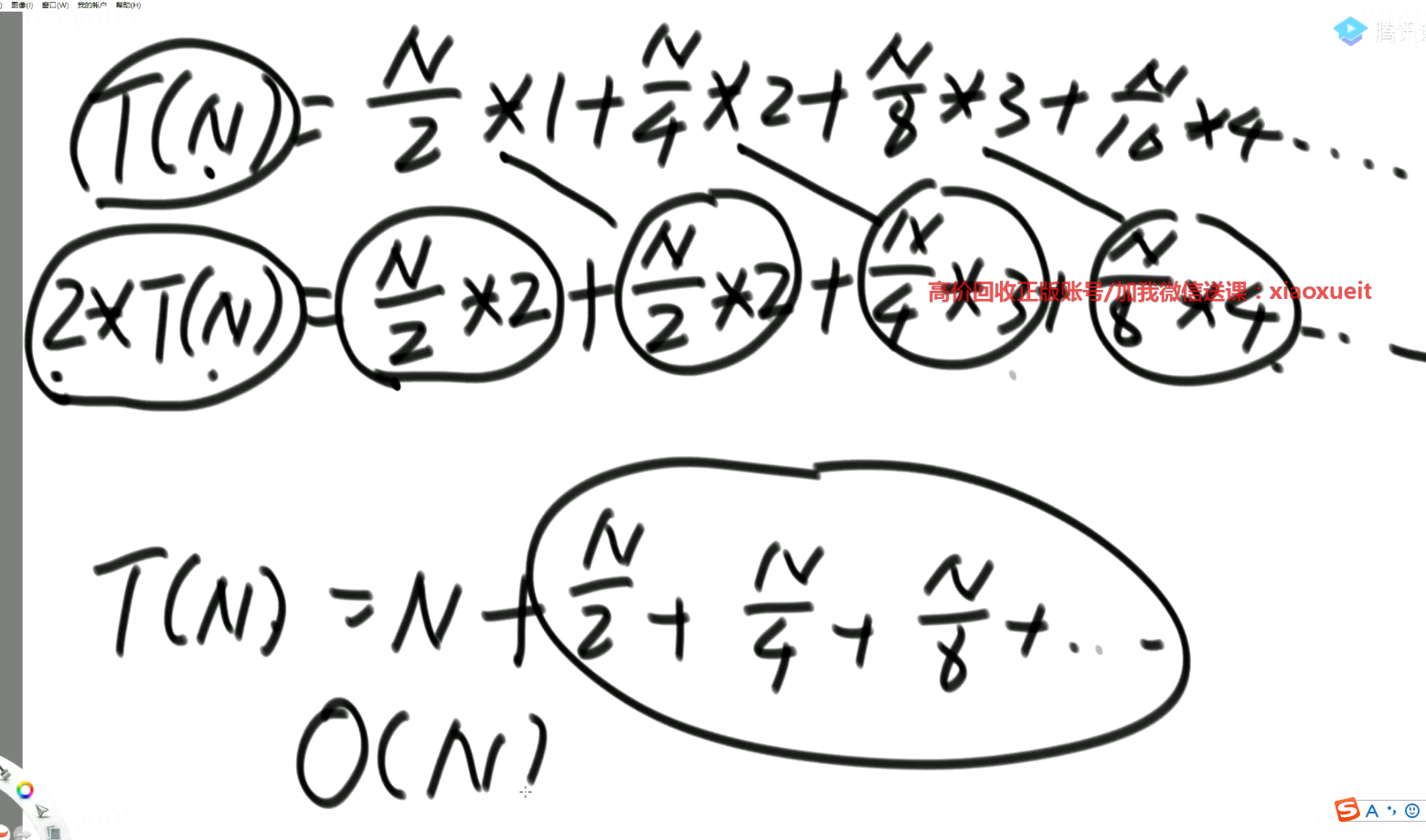
堆空間的額外空間復雜度為:O(1);
**總結:**
1. 堆結構就是用數組實現的完全二叉樹結構。
2. 完全二叉樹中如果每棵子樹的最大值都在頂部就是大根堆。
3. 完全二叉樹如果每棵子樹的最小值都在頂部就是小根堆。
4. 堆結構兩個主要的操作是heapInsert和heapify。
5. 優先級隊列結構就是堆結構。
堆結構中重要的是heapInsert和heapify結構,并且經常在代碼實現中重寫堆結構而不用語言提供的堆結構。
使用系統的堆的結構時,如果存進去的是對象,則中途改變對象的內容,堆結構很可能不會繼續維護正確的結構。因此可以自己手寫一個堆來實現,使用一個HashMap來記錄在堆上的位置:
`Code:`
~~~
?public static class MyHeap<T> {
? ? ?private ArrayList<T> heap;
? ? ?private HashMap<T, Integer> indexMap;
? ? ?private int heapSize;
? ? ?private Comparator<? super T> comparator;
??
? ? ?public MyHeap(Comparator<? super T> comparator) {
? ? ? ? ?heap = new ArrayList<>();
? ? ? ? ?indexMap = new HashMap<>();
? ? ? ? ?heapSize = 0;
? ? ? ? ?this.comparator = comparator;
? ? }
??
? ? ?public boolean isEmpty() {
? ? ? ? ?return heapSize == 0;
? ? }
??
? ? ?public int size() {
? ? ? ? ?return heapSize;
? ? }
??
? ? ?/**
? ? ? ? ? * 判斷某個鍵是否存在
? ? ? ? ? * @param key
? ? ? ? ? * @return
? ? ? ? ? */
? ? ?public boolean contains(T key) {
? ? ? ? ?return indexMap.containsKey(key);
? ? }
??
??
? ? ?public void push(T value) {
? ? ? ? ?heap.add(value);
? ? ? ? ?indexMap.put(value, heapSize);
? ? ? ? ?heapInsert(heapSize++);
? ? }
??
? ? ?public T pop() {
? ? ? ? ?T ans = heap.get(0);
? ? ? ? ?int end = heapSize - 1;
? ? ? ? ?swap(0, end);
? ? ? ? ?// 移除最后一個元素
? ? ? ? ?heap.remove(end);
? ? ? ? ?// 移除映射元素
? ? ? ? ?indexMap.remove(ans);
? ? ? ? ?// 重新調整堆結構
? ? ? ? ?heapify(0, --heapSize);
? ? ? ? ?return ans;
? ? }
??
? ? ?/**
? ? ? ? ? * 從下往上調整堆結構
? ? ? ? ? * @param index
? ? ? ? ? */
? ? ?private void heapInsert(int index) {
? ? ? ? ?while (comparator.compare(heap.get(index), heap.get((index - 1) / 2)) > 0) {
? ? ? ? ? ? ?swap(index, (index - 1) / 2);
? ? ? ? ? ? ?index = (index - 1) / 2;
? ? ? ? }
? ? }
??
? ? ?/**
? ? ? ? ? * 從上往下調整堆結構
? ? ? ? ? * @param index
? ? ? ? ? * @param heapSize
? ? ? ? ? */
? ? ?private void heapify(int index, int heapSize) {
? ? ? ? ?int left = index * 2 + 1;
? ? ? ? ?while (left < heapSize) {
? ? ? ? ? ? ?left = left + 1 < heapSize && comparator.compare(heap.get(left), heap.get(left + 1)) > 0 ? left : left + 1;
? ? ? ? ? ? ?left = comparator.compare(heap.get(index), heap.get(left)) > 0 ? index : left;
? ? ? ? ? ? ?if (left == index) {
? ? ? ? ? ? ? ? ?break;
? ? ? ? ? ? }
? ? ? ? ? ? ?swap(left, index);
? ? ? ? ? ? ?index = left;
? ? ? ? ? ? ?left = index * 2 + 1;
? ? ? ? }
? ? }
??
? ? ?private void swap(int index1, int index2) {
? ? ? ? ?T t = heap.get(index1);
? ? ? ? ?T t1 = heap.get(index2);
? ? ? ? ?heap.set(index1, t1);
? ? ? ? ?heap.set(index2, t);
? ? ? ? ?indexMap.put(t, index2);
? ? ? ? ?indexMap.put(t1, index1);
? ? }
?}
~~~
**堆排序**
* 先讓整個數組都變成大根堆結構,建立堆的過程:
* 從上到下的方法heapify,時間復雜度為O(N\*logN);
* 從下到上的方法heapInsert,時間復雜度為O(N);
* 把堆的最大值和堆末尾的值交換,然后減少堆的大小后,再次調整堆,一直周而復始,時間復雜度為O(N \* logN);
* 堆的大小減小為0之后,排序成功。
系統實現的堆結構:默認是小根堆的實現。
~~~
?PriorityQueue<Integer> heap = new PriorityQueue<>();
~~~
> 題目:已知一個幾乎有序的數組,如果把數組排好順序之后,每個元素移動的距離一定不超過K,并且K相對于長度來說是比較小的。
>
> 請選擇一個合適的排序策略,對這個數組進行排序。
`Code:`
思路:將前面k+1個元素放入小根堆中,然后彈出堆根,插入第k+2,一直執行這個過程。理由是每個元素移動的距離不超過K。
~~~
?public void sortedArrDistanceLessK(int[] arr, int k) {
? ? ?// 創建小根堆結構
? ? ?PriorityQueue<Integer> heap = new PriorityQueue<>();
? ? ?int index = 0;
? ? ?for (; index <= Math.min(arr.length, k); index++) {
? ? ? ? ?heap.add(arr[index]);
? ? }
? ? ?int i = 0;
? ? ?for (; index < arr.length; i++, index++) {
? heap.add(arr[index]);
? ? ? ? ?// 重新設置值,可以保證排好序
? ? ? ? ?arr[i] = heap.poll();
? ? }
? ? ?while (!heap.isEmpty()) {
? ? ? ? ?arr[i++] = heap.poll();
? ? }
?}
~~~
時間復雜度為:O(N\*lgk);
**其他**
PriorityQueue不是線程安全的,線程安全的為PriorityBlockingQueue隊列,其操作用可重入鎖進行同步操作。
