# 查找數組中的局部最小值
對于查找數組中的局部最小值可以分為如下**三種情況**,即:
- 對于數組首部:如果`arr[0] < arr[1]`,那么`arr[0]`為局部最小;
- 對于數組尾部:如果`arr[n-2] > arr[n-1]`,那么`arr[n-1]`為局部最小值;
- 對于其余任意位置`i`:需要滿足`arr[i-1]>arr[i]`,且`arr[i]<arr[i+1]`;
那么編程應該首先考慮邊界問題,最后對于非邊界情況滿足下圖:
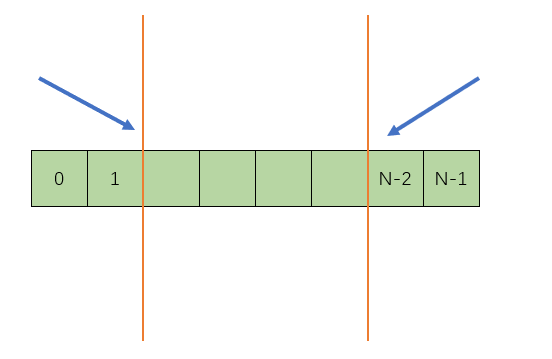
那么也就是說,如果在首尾邊界都沒有找到局部最小值,而我們確定數列中存在局部最小。那么應該滿足上圖的情況。
那么,在下標`[2...n-3]`位置中必然存在滿足條件的局部最小值。所以本題可以使用二分來進行查找。即代碼為:
~~~
public int localMinimum(int[] arr) {
int len = 0;
if (arr == null || (len = arr.length) == 0 || len < 2) return -1;
// 首尾邊界情況
if (arr[0] < arr[1]) return 0;
if (arr[len - 1] < arr[len - 2]) return len - 1;
int left = 0, right = arr.length - 1;
while (left < right) {
int mid = (left + right) / 2;
if (mid >= 1 && mid < len - 1 &&
arr[mid] < arr[mid + 1] && arr[mid] < arr[mid - 1]) { // 當前滿足局部最小值
return mid;
} else if (mid >= 1 && arr[mid] > arr[mid - 1]) { // 局部最小值在左側
right = mid - 1;
} else if (mid < len - 1 && arr[mid] > arr[mid + 1]) { // 局部最小值在右側
left = mid + 1;
}
}
return -1;
}
~~~
對應情況可以繼續用下面的圖表示:
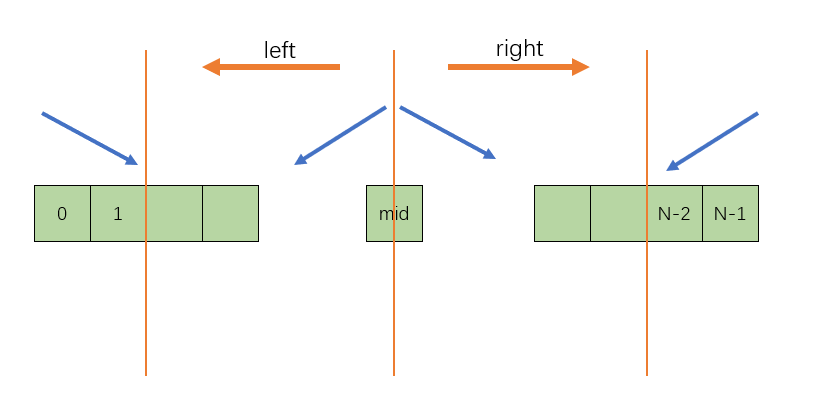
可以參考:[162. 尋找峰值 - 力扣(LeetCode) (leetcode-cn.com)](https://leetcode-cn.com/problems/find-peak-element/)
