[toc]
# 二、Java集合與數據結構
容器主要包括 Collection 和 Map 兩種,Collection 存儲著對象的集合,而 Map 存儲著鍵值對(兩個對象)的映射表。
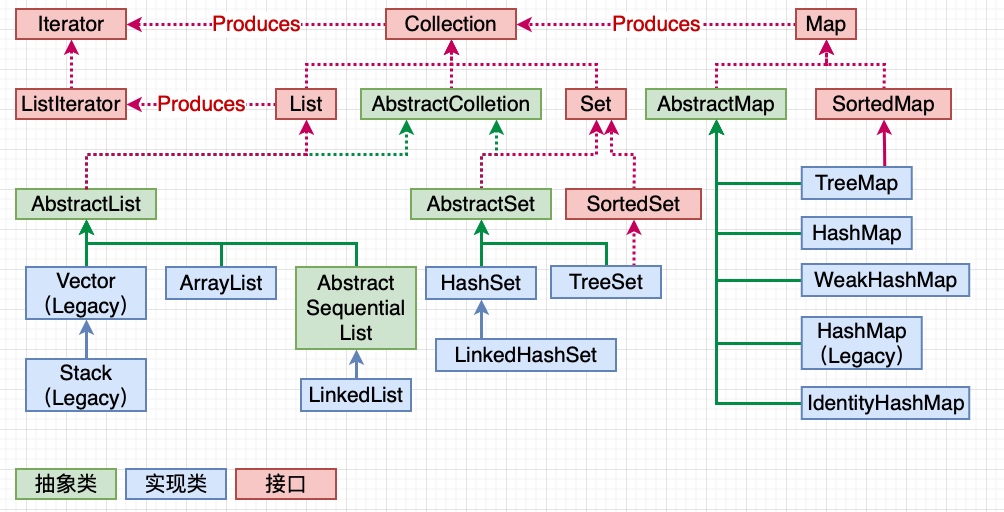
`List`是**有序隊列**,List中可以*有重復*的元素
`Set`是**數學組集合**概念,*沒有重復*元素
為了方便,抽象出了AbstractCollection抽象類,它實現了Collection中的絕大部分函數;這樣,在Collection的實現類中,我們就可以通過繼承AbstractCollection省去重復編碼。AbstractList和AbstractSet都繼承于AbstractCollection,具體的List實現類繼承于AbstractList,而Set的實現類則繼承于AbstractSet。
Collection中有一個iterator()函數,它的作用是返回一個Iterator接口。通常,我們通過Iterator迭代器來遍歷集合。ListIterator是List接口所特有的,在List接口中,通過ListIterator()返回一個ListIterator對象。
## 1、概覽
### 1.1、集合Collection
#### 1.1.1 Set
* `TreeSet`:基于**紅黑樹**實現,支持**有序性**操作,例如根據一個范圍查找元素的操作。但是查找效率不如 HashSet,HashSet 查找的時間復雜度為 O(1),TreeSet 則為 O(logN)。
* `HashSet`:基于**哈希表**實現,支持*快速查找*,但*不支持有序*性操作。并且失去了元素的插入順序信息,也就是說使用 Iterator 遍歷 HashSet 得到的結果是不確定的。
* `LinkedHashSet`:具有 HashSet 的查找效率,并兼顧**有序性**,且內部使用**雙向鏈表**維護元素的插入*順序*。
#### 1.1.2 List
* `ArrayList`:基于**動態數組**實現,支持***隨機訪問***,查找快,增刪慢。
* `Vector`:和 ArrayList 類似,但它是*線程安全*的。
* `LinkedList`:基于**雙向鏈表**實現,只能***順序訪問***,增刪快,查找慢。不僅如此,LinkedList 還可以用作棧、隊列和雙向隊列。
#### 1.1.3 Queue
* `LinkedList`:可以用它來實現*雙向隊列*。
* `PriorityQueue`:基于**堆結構**實現,可以用它來實現*優先隊列*。
### 1.2、Map
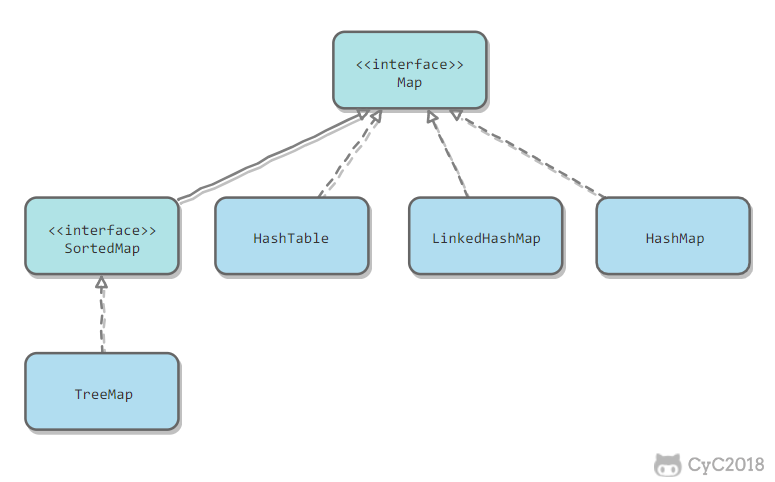
* `TreeMap`:基于**紅黑樹**實現。
* `HashMap`:基于**哈希表**實現。
* `HashTable`:和 HashMap 類似,但它是*線程安全*的,這意味著同一時刻多個線程可以同時寫入 HashTable 并且不會導致數據不一致。它是遺留類,不應該去使用它。現在可以使用**ConcurrentHashMap** 來支持線程安全,并且 ConcurrentHashMap 的效率會更高,因為 ConcurrentHashMap 引入了*分段鎖*。
* `LinkedHashMap`:使用**雙向鏈表**來維護元素的*順序*,順序為*插入順序*或者*最近最少使用(LRU)順序*。
## 2、源碼分析
### 2.1 ArrayList
因為 ArrayList 是基于**數組(Object[] elementData)**實現的,所以支持快速隨機訪問。RandomAccess 接口標識著該類支持快速隨機訪問。
```java
public class ArrayList<E> extends AbstractList<E>
implements List<E>, RandomAccess,
Cloneable, java.io.Serializable
```
#### 2.1.1 添加元素及擴容
添加元素時使用 **ensureCapacityInternal()** 方法來保證容量足夠,如果不夠時,需要使用 *grow()* 方法進行擴容,新容量的大小為 `oldCapacity + (oldCapacity >> 1)`,也就是舊容量的 1.5 倍,如果新容量大于擴容后的容量,直接將新容量作為擴容的容量。
擴容操作需要調用 `Arrays.copyOf()` 把原數組整個復制到新數組中,這個操作代價很高,因此最好在創建 ArrayList 對象時就指定大概的容量大小,減少擴容操作的次數。
**以無參數構造方法創建 ArrayList 時,實際上初始化賦值的是一個空數組。當真正對數組進行添加元素操作時,才真正分配容量。即向數組中添加第一個元素時,數組容量擴為10**
```java
/**
* 在此列表中的指定位置插入指定的元素。
* 先調用 rangeCheckForAdd 對index進行界限檢查;
* 然后調用 ensureCapacityInternal 方法保證capacity足夠大;
* 再將從index開始之后的所有成員后移一個位置;
* 將element插入index位置;最后size加1。
*/
public void add(int index, E element) {
rangeCheckForAdd(index);
// Increments modCount!!
ensureCapacityInternal(size + 1);
//arraycopy()這個實現數組之間復制的方法一定要看一下,
//下面就用到了arraycopy()方法實現數組自己復制自己
System.arraycopy(elementData, index, elementData,
index + 1,size - index);
elementData[index] = element;
size++;
}
private void rangeCheckForAdd(int index) {
if (index > size || index < 0)
throw new IndexOutOfBoundsException(outOfBoundsMsg(index));
}
```
#### 2.1.2 刪除元素
需要調用 `System.arraycopy()` 將 index+1 后面的元素都復制到 index 位置上,該操作的時間復雜度為 O(N),可以看出 ArrayList 刪除元素的代價是非常高的。
```java
/**
* 從列表中刪除指定元素的第一個出現(如果存在)。
* 如果列表不包含該元素,則它不會更改。
* 返回true,如果此列表包含指定的元素
*/
public boolean remove(Object o) {
if (o == null) {
for (int index = 0; index < size; index++)
if (elementData[index] == null) {
fastRemove(index);
return true;
}
} else {
for (int index = 0; index < size; index++)
if (o.equals(elementData[index])) {
fastRemove(index);
return true;
}
}
return false;
}
private void fastRemove(int index) {
modCount++;
int numMoved = size - index - 1;
if (numMoved > 0)
System.arraycopy(elementData,
index+1, elementData, index,numMoved);
elementData[--size] = null; // clear to let GC do its work
}
```
#### 2.1.3 Fail-fast
`modCount` 用來記錄 ArrayList 結構**發生變化的次數**。結構發生變化是指**添加**或者**刪除**至少一個元素的所有操作,或者是調整內部數組的大小,僅僅只是設置元素的值不算結構發生變化。
在進行**序列化**或者**迭代**等操作時,需要**比較操作前后 modCount**(在AbstractList中定義)**是否改變**,如果改變了需要拋出 ConcurrentModificationException。
#### 2.1.4 序列化
ArrayList 基于數組實現,并且具有**動態擴容**特性,因此保存元素的數組不一定都會被使用,那么就**沒必要全部**進行**序列化**。
保存元素的數組 `elementData` 使用 `transient` 修飾,該關鍵字聲明數組默認不會被序列化。ArrayList 實現了 `writeObject()` 和 `readObject()` 來控制只序列化數組中**有元素填充那部分**內容。
#### 2.1.5 System.arraycopy() & Arrays.copyOf()
```java
public static native void
arraycopy(Object src,int srcPos,Object dest,int destPos,int length);
```
`src`:the source array.**源數組**;
`srcPos`:starting position in the source array.**源數組**要復制的*起始位置*
`est`:the destination array.**目標數組**(將原數組復制到目標數組)
`destPos` :starting position in the destination data.**目標數組***起始位置*(從目標數組的哪個下標開始復制操作)
`length`:the number of array elements to be copied.復制源數組的**長度**(從srcPos開始復制幾個)
Arrays.copyOf() 內部實際調用了 System.arraycopy()方法,它的返回值時一個新的數組
#### 2.1.6 ArrayList繼承AbstractList為什么還要實現List
如果不實現List,使用Class.getInterfaces時無法獲取到對應的接口,可能在實現代理時出現問題。
#### 2.1.7 快速失敗(fail-fast) 和安全失敗(fail-safe)
**一:快速失敗(fail—fast)**
在用迭代器遍歷一個集合對象時,如果遍歷過程中對集合對象的內容進行了修改(增
加、刪除、修改),則會拋出 Concurrent Modification Exception。
**原理:**迭代器在遍歷時直接訪問集合中的內容,并且在遍歷過程中使用一個 modCo
unt 變量。集合在被遍歷期間如果內容發生變化,就會改變 modCount 的值。每當迭代器使
用 hashNext()/next()遍歷下一個元素之前,都會檢測 modCount 變量是否為 expectedmod
Count 值,是的話就返回遍歷;否則拋出異常,終止遍歷。
**注意:**這里異常的拋出條件是檢測到 modCount!=expectedmodCount 這個條件。如
果集合發生變化時修改 modCount 值剛好又設置為了 expectedmodCount 值,則異常不會
拋出。因此,不能依賴于這個異常是否拋出而進行并發操作的編程,這個異常只建議用于檢
測并發修改的 bug。
**場景:**java.util 包下的集合類都是快速失敗的,不能在多線程下發生并發修改(迭代過
程中被修改)。
**二:安全失敗(fail—safe)**
采用安全失敗機制的集合容器,在遍歷時不是直接在集合內容上訪問的,而是先復制原
有集合內容,在拷貝的集合上進行遍歷。
**原理:**由于迭代時是對原集合的拷貝進行遍歷,所以在遍歷過程中對原集合所作的修改
并不能被迭代器檢測到,所以不會觸發 Concurrent Modification Exception。
**缺點:**基于拷貝內容的優點是避免了 Concurrent Modification Exception,但同樣地,
迭代器并不能訪問到修改后的內容,即:迭代器遍歷的是開始遍歷那一刻拿到的集合拷貝,
在遍歷期間原集合發生的修改迭代器是不知道的。
**場景:**java.util.concurrent 包下的容器都是安全失敗,可以在多線程下并發使用,并
發修改。
快速失敗和安全失敗是對迭代器而言的。 快速失敗:當在迭代一個集合的時候,如果有另
外一個線程在修改這個集合,就會拋出 ConcurrentModification 異常,java.util 下都是快速
失敗。 安全失敗:在迭代時候會在集合二層做一個拷貝,所以在修改集合上層元素不會影
響下層。在 java.util.concurrent 下都是安全失敗
### 2.2 Vector
>1. `ArrayList` 是 `List` 的主要實現類,底層使用 `Object[ ]`存儲,適用于頻繁的查找工作,線程不安全 ;
>2. `Vector` 是 `List` 的古老實現類,底層使用 `Object[ ]`存儲,線程安全的。
它的實現與 ArrayList 類似,但是使用了 `synchronized` 進行同步。
* `Vector` 是**同步**的,因此**開銷**就比 ArrayList 要**大**,訪問速度更慢。最好使用 ArrayList 而不是 Vector,因為同步操作完全可以由程序員自己來控制;
* `Vector` 每次**擴容**請求其大小的 **2 倍**(也可以通過構造函數設置增長的容量),而 `ArrayList` 是 **1.5 倍**
**ArrayList線程安全的方案:**
可以使用 Collections.synchronizedList()得到一個線程安全的 ArrayList。
```java
List<String> list = new ArrayList<>();
List<String> synList = Collections.synchronizedList(list);
```
也可以使用 concurrent 并發包下的 CopyOnWriteArrayList 類。
```java
List<String> list = new CopyOnWriteArrayList<>();
```
### 2.3 LinkedList
基于雙向鏈表實現,使用 Node 存儲鏈表節點信息。
```java
private static class Node<E> {
E item;
Node<E> next;
Node<E> prev;
}
```
每個鏈表存儲了 first 和 last 指針:
```java
transient Node<E> first;
transient Node<E> last;
```

LinkedList是通過雙向鏈表的,如何實現get(index)方法?它就是通過一個**計數索引值**來實現的。例如,當我們調用get(int location)時,首先會比較“location”和“雙向鏈表長度的1/2”;若前者大,則從鏈表頭開始往后查找,直到location位置;否則,從鏈表末尾開始先前查找,直到location位置。
### 2.4 Arraylist 與 LinkedList 區別?
* **1.是否保證線程安全**:ArrayList 和 LinkedList 都是不同步的,也就是*不保證線程安全*;
* **2. 底層數據結構**:Arraylist底層使用的是*Object 數組*;LinkedList底層使用的是 *雙向鏈表*(JDK1.6之前為循環鏈表,JDK1.7取消了循環。注意雙向鏈表和雙向循環鏈表的區別,下面有介紹到!)
* **3. 插入和刪除是否受元素位置的影響**:
* ① `ArrayList`采用*數組*存儲,所以*插入*和*刪除*元素的時間復雜度*受元素位置的影響*。比如:執行add(E e) 方法的時候, ArrayList會默認在將指定的元素追加到此列表的末尾,這種情況時間復雜度就是O(1)。但是如果要在指定位置 i 插入和刪除元素的話(add(int index, E element) )時間復雜度就為 O(n-i)。因為在進行上述操作的時候集合中第 i 和第 i 個元素之后的(n-i)個元素都要執行向后位/向前移一位的操作。
* ② `LinkedList` 采用*鏈表*存儲,所以*插入,刪除*元素時間復雜度*不受元素位置的影響*,都是近似 O(1)而數組為近似 O(n)。
* **4. 是否支持快速隨機訪問**:`LinkedList`*不支持*高效的隨機元素訪問,而`ArrayList`*支持*。快速隨機訪問就是通過元素的序號快速獲取元素對象(對應于get(int index) 方法)。
* **5. 內存空間占用:** `ArrayList`的空 間浪費主要體現在在*list列表的結尾*會預留一定的容量空間,而`LinkedList`的空間花費則體現在它的*每一個元素*都需要消耗比ArrayList更多的空間(因為要存放直接后繼和直接前驅以及數據)。
### 2.5 HashTable
#### 2.5.1 參數
(1)table 是一個 Entry[]數組類型,而 Entry 實際上就是一個單向鏈表。哈希表的"key-value 鍵值對"都是存儲在 Entry 數組中的。
(2)count 是 Hashtable 的大小,它是 Hashtable 保存的鍵值對的數量。
(3)threshold 是 Hashtable 的閾值,用于判斷是否需要調整 Hashtable 的容量。threshold 的值="容量*加載因子"。
(4)loadFactor 就是加載因子。
(5)modCount 是用來實現 fail-fast 機制的
#### 2.5.2 put
從下面的代碼中我們可以看出,Hashtable 中的 key 和 value 是不允許為空的,當我們想要想 Hashtable 中添加元素的時候,首先計算 key 的 hash 值,然后通過 hash 值確定在 table 數組中的索引位置,最后將 value 值替換或者插入新的元素,如果容器的數量達到閾值,就會進行擴充。
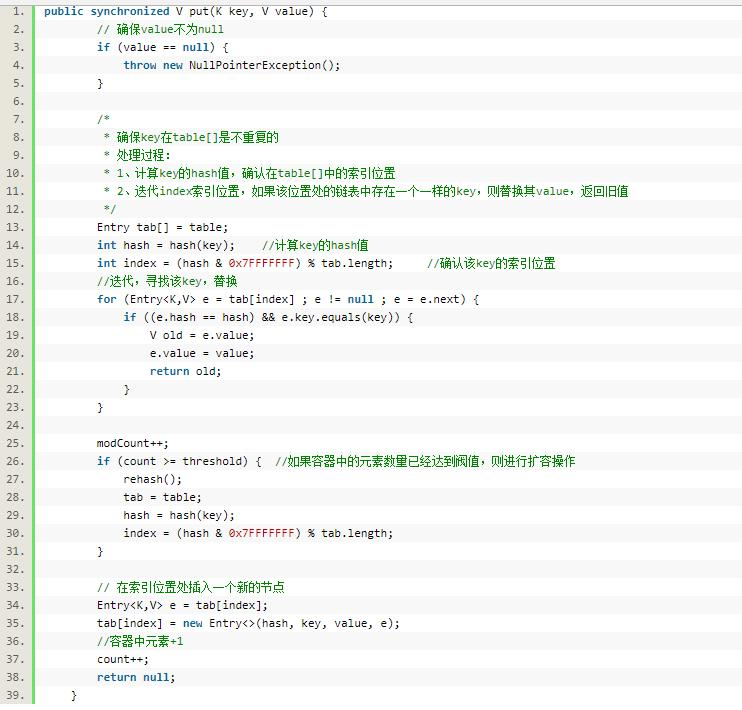
#### 2.5.3 get

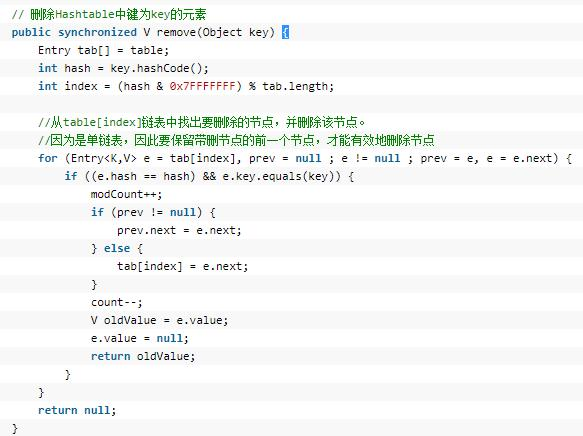
#### 2.5.4 Remove
在下面代碼中,如果 prev 為 null 了,那么說明第一個元素就是要刪除的元素,那么就直接指向第一個元素的下一個即可。
#### 2.5.5 擴容
- 默認初始容量為 11線程安全,但是速度慢,不允許 key/value 為 null
- 加載因子為 0.75:即當 元素個數 超過 容量長度的 0.75 倍 時,進行擴容
- 擴容增量:2*原數組長度+1
如 HashTable 的容量為 11,一次擴容后是容量為 23
### 2.6 HashMap
>HashMap *允許 null* 鍵和 null 值,在計算哈鍵的哈希值時,null 鍵哈希值為 0。HashMap 并*不保證鍵值對的順序*(LinkedHashMap解決這個問題),這意味著在進行某些操作后,鍵值對的順序可能會發生變化。另外,需要注意的是,HashMap 是*非線程安全*類,在多線程環境下可能會存在問題。
#### 2.6.1 JDK1.7版本
內部包含了一個 Entry 類型的數組 table。初始化容量為16,負載因子為0.75
```java
transient Entry[] table;
static class Entry<K,V> implements Map.Entry<K,V> {
final K key;
V value;
Entry<K,V> next;
int hash;
```
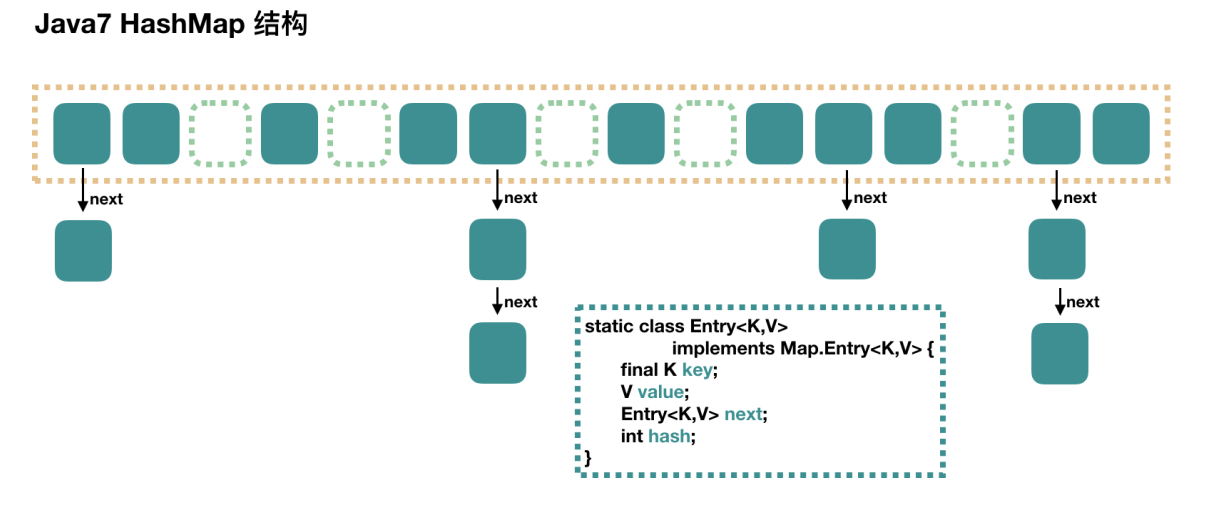
大方向上, HashMap 里面是一個數組,然后數組中每個元素是一個單向鏈表。上圖中,每個綠色的實體是嵌套類 Entry 的實例, Entry 包含四個屬性: key, value, hash 值和用于單向鏈表的 next。
1. capacity:當前數組容量,始終保持 2^n,擴容后數組大小為當前的 2 倍。
2. oadFactor:負載因子,默認為 0.75。
3. threshold:擴容的閾值,等于 capacity * loadFactor
Java8 對 HashMap 進行了一些修改, 最大的不同就是利用了紅黑樹,所以其由 數組+鏈表+紅黑樹 組成。根據 Java7 HashMap 的介紹,我們知道,查找的時候,根據 hash 值我們能夠快速定位到數組的具體下標,但是之后的話, 需要順著鏈表一個個比較下去才能找到我們需要的,時間復雜度取決于鏈表的長度,為 O(n)。為了降低這部分的開銷,在 Java8 中, 當鏈表中的元素超過了 8 個以后,
會將鏈表轉換為紅黑樹,在這些位置查找的時候可以降低時間復雜度為O(logN)。
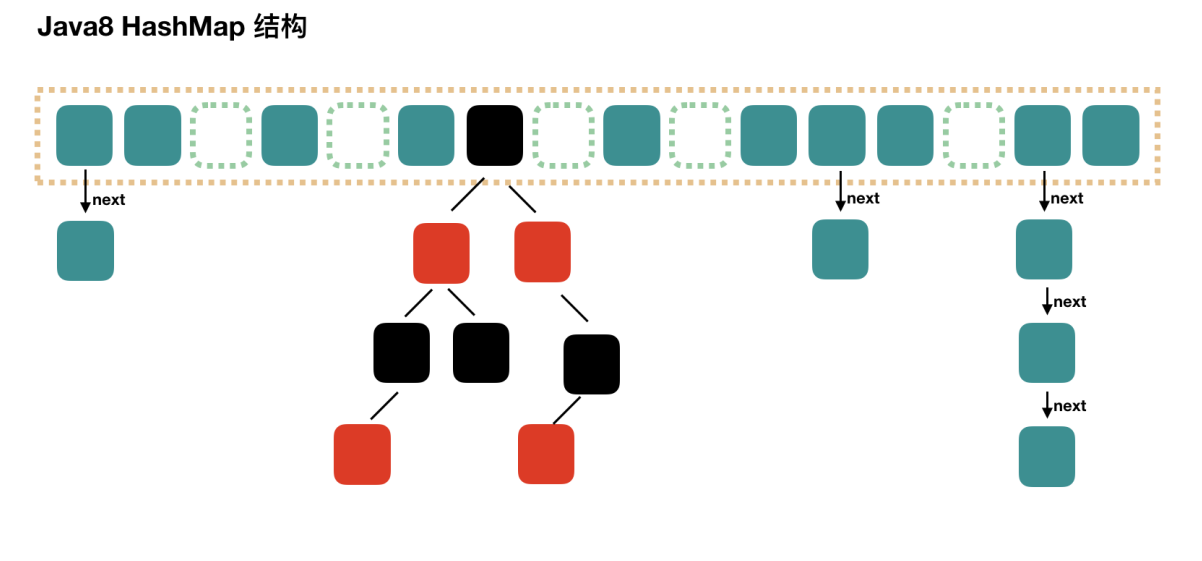
#### 2.6.2 存儲
Entry 存儲著鍵值對。它包含了四個字段,從 next 字段我們可以看出 Entry 是一個鏈表。即數組中的每個位置被當成一個桶,一個桶存放一個鏈表。HashMap 使用**拉鏈法**來解決沖突,同一個鏈表中存放哈希值和散列桶取模運算結果相同的 Entry。
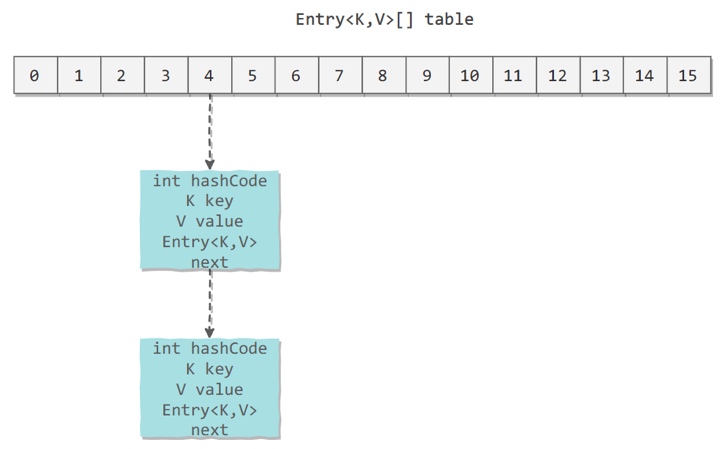
應該注意到鏈表的插入是以**頭插法**方式進行的,哈希沖突時插入在鏈表頭部。
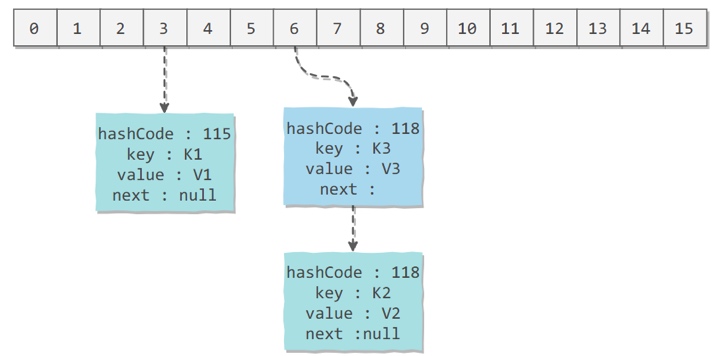
為了能讓 HashMap 存取高效,盡量較少碰撞,也就是要盡量把數據分配均勻。Hash 值的范圍值-2147483648到2147483647,前后加起來大概40億的映射空間,只要哈希函數映射得比較均勻松散,一般應用是很難出現碰撞的。但問題是一個40億長度的數組,內存是放不下的。所以這個散列值是不能直接拿來用的。用之前還要先做對數組的長度取模運算,得到的余數才能用來要存放的位置也就是對應的數組下標。可能會想到采用%取余的操作來實現。`hash%table.length`
但是,重點來了:**“取余(%)操作中如果除數是2的冪次則等價于與其除數減一的與(&)操作(也就是說 hash%length==hash&(length-1)的前提是 length 是2的 n 次方;)。”** 并且 **采用二進制位操作 &,相對于%能夠提高運算效率,這就解釋了 HashMap 的長度為什么是2的冪次方** 此外,使`lenght-1`的全部位為1,能使計算出來的下標分布更均勻,減少哈希碰撞。*在擴容相關的transfer方法中,也有調用indexFor重新計算下標。容量設計成2的n次冪能使擴容時重新計算的下標相對穩定,減少移動元素
#### 2.6.3 查找 get
查找需要分成兩步進行:
* 計算鍵值對所在的桶;
* 在鏈表上順序查找,時間復雜度顯然和鏈表的長度成正比。

#### 2.6.4 插入 put
HashMap **允許插入**鍵為 null 的鍵值對。但是因為無法調用 null 的 hashCode() 方法,也就無法確定該鍵值對的桶下標,只能通過*強制指定一個桶下標來存*放。HashMap 使用*第 0 個*桶存放鍵為 null 的鍵值對。*因此 HashMap 最多只允許一條記錄的鍵為 null,允許多條記錄的值為 null。*
*這里 HashMap 里面用到鏈式數據結構的一個概念。上面我們提到過 Entry 類里面有一個 next 屬性,作用是指向下一個 Entry。打個比方, 第一個鍵值對 A 進來,通過計算其 key 的 hash 得到的 index=0,記做:Entry[0] = A。一會后又進來一個鍵值對 B,通過計算其 index 也等于 0,現在怎么辦?HashMap 會這樣做:B.next = A,Entry[0] = B,如果又進來 C,index 也等于 0,那么 C.next = B,Entry[0] = C;這樣我們發現 index=0 的地方其實存取了 A,B,C 三個鍵值對,他們通過 next 這個屬性鏈接在一起。所以疑問不用擔心。也就是說數組中存儲的是最后插入的元素。到這里為止,HashMap 的大致實現。*

#### 2.6.5 擴容
設 HashMap 的 table 長度為 M,需要存儲的鍵值對數量為 N,如果哈希函數滿足均勻性的要求,那么每條鏈表的長度大約為 N/M,因此平均查找次數的復雜度為 $O(N/M)$。為了讓查找的成本降低,應該盡可能使得 N/M 盡可能小,因此需要保證 M 盡可能大,也就是說 table 要盡可能大。
- `capacity`:當前數組容量,始終保持2^n,默認為16。擴容是擴充為當前的2倍
- `size`:當前鍵值對的數量
- `threshold`:size的臨界值,大于等于threshold就需要擴容。**threshold = (int)(Capacity * loadFactor)**
- `load_factor`:負載因子,默認值為*0.75*
HashMap 構造函數允許用戶傳入的容量不是 2 的 n 次方,因為它可以自動地將傳入的容量轉換為 2 的 n 次方。
#### 2.6.6 與 HashTable 的比較
* HashTable的方法是同步的,HashMap未經同步,所以在多線程場合要手動同步HashMap這個區別就像Vector和ArrayList一樣。
* HashTable不允許null值(key和value都不可以),HashMap允許null值(key和value都可以)。
* HashMap 的迭代器是 fail-fast 迭代器。
* HashMap 不能保證隨著時間的推移 Map 中的元素次序是不變的。
* HashTable中hash數組默認大小是11,增加的方式是 old*2+1。HashMap中hash數組的默認大小是16,而且一定是2的指數。
* 哈希值的使用不同,HashTable直接使用對象的hashCode,代碼是這樣的:
```java
int hash = key.hashCode();
int index = (hash & 0x7FFFFFFF) % tab.length;
```
而HashMap重新計算hash值,而且用與代替求模:
```java
int hash = hash(k);
int i = indexFor(hash, table.length);
static int hash(Object x) {
int h = x.hashCode();
h += ~(h << 9);
h ^= (h >>> 14);
h += (h << 4);
h ^= (h >>> 10);
return h;
}
static int indexFor(int h, int length) {
return h & (length-1);
}
```
#### 2.6.7 多線程死循環
是多線程**同時put**時,如果同時觸發了**rehash操作**,會導致HashMap中的鏈表中出現**循環節點**,進而使得后面get的時候,會死循環。因為會將同一鏈表的值翻轉,當一個線程完成翻轉后,第二個線程再次翻轉就會出現死循環問題。(transfor方法,第二個線程的第三次循環會出問題)

要想實現線程安全,那么需要調用 collections 類的靜態方法
synchronizeMap()實現
#### 2.6.8 JDK1.8版本
當鏈表長度大于閾值(默認為8)時,將鏈表轉化為紅黑樹,以減少搜索時間。
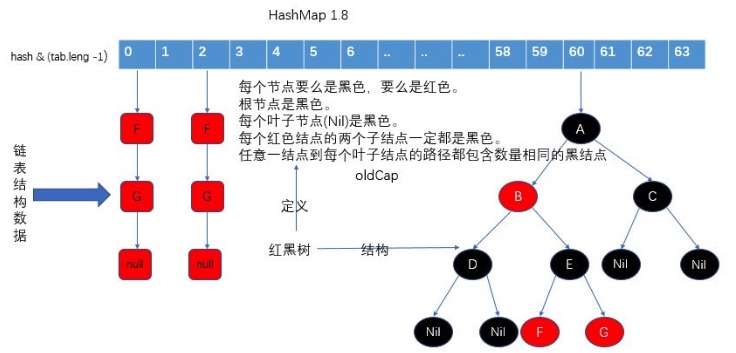
擴容時需要把鍵值對重新放到對應的桶上,采用一個特殊機制,降低重新計算桶下標的操作。只需要看看原來的hash值新增的那個bit是1還是0就好了,是0的話索引沒變,是1的話索引變成“原索引+oldCap”
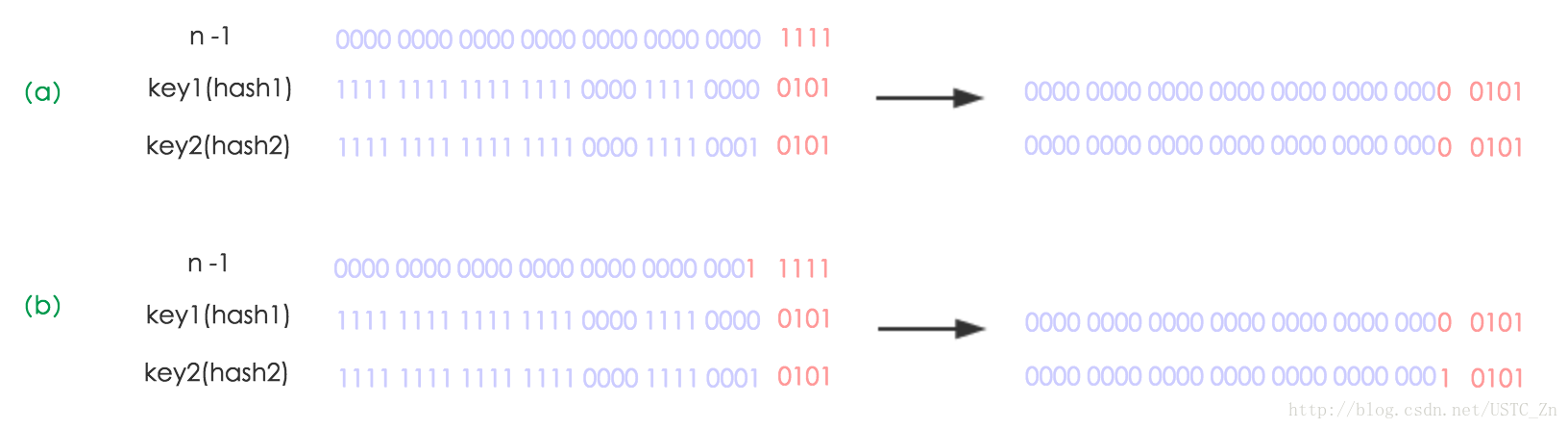
其中n為table的長度。
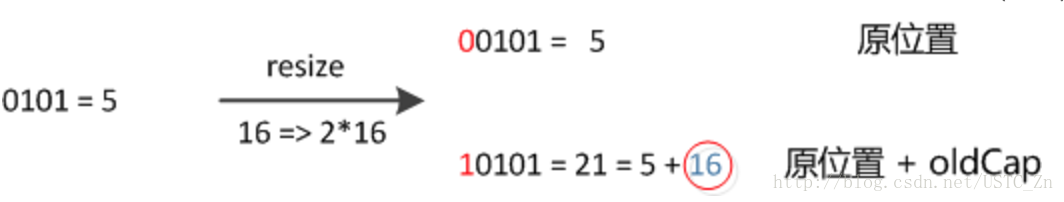

>參考:
>【HashMap 源碼淺析 1.8】https://blog.51cto.com/14220760/2363572
>【Java 8系列之重新認識HashMap】https://zhuanlan.zhihu.com/p/21673805
#### 2.6.9 哈希沖突詳解
一般來說哈希沖突有兩大類**解決方式**
1. Separate chaining
2. Open addressing
Java 中采用的是第一種 Separate chaining,即在發生碰撞的那個桶后面再加一條“鏈”來存儲,那么這個“鏈”使用的具體是什么數據結構,不同的版本稍有不同:
在 JDK1.6 和 1.7 中,是用**鏈表**存儲的,這樣如果碰撞很多的話,就變成了在鏈表上的查找,worst case 就是 O(n);
在 JDK 1.8 進行了優化,當鏈表長度較大時(超過 8),會采用**紅黑樹**來存儲,這樣大大提高了查找效率。
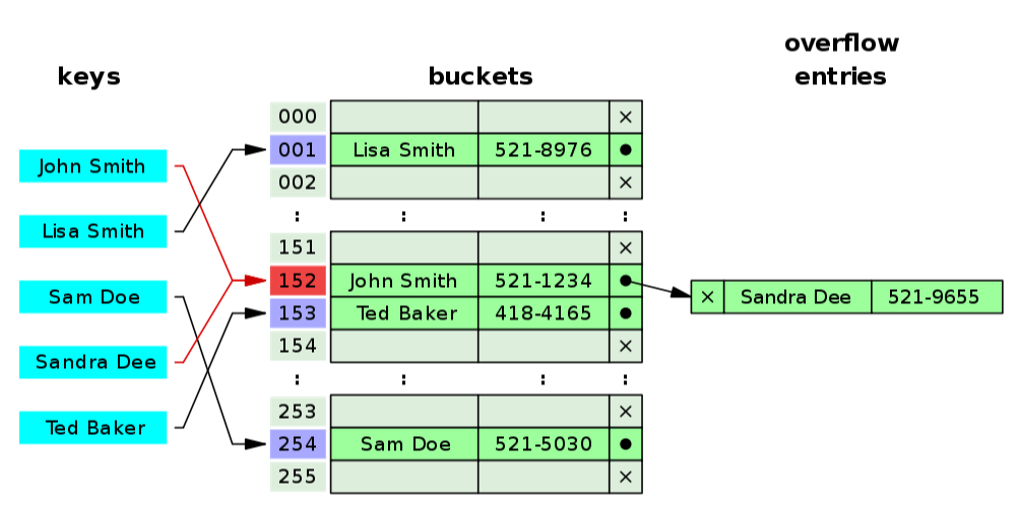
第二種方法 open addressing 也是非常重要的思想,因為在真實的分布式系統里,有很多地方會用到 hash 的思想但又不適合用 seprate chaining。
這種方法是順序查找,如果這個桶里已經被占了,那就按照“**某種方式**”繼續找下一個沒有被占的桶,直到找到第一個空的。
<img src="https://i.loli.net/2020/12/23/BK8qx7cADzkIOnt.png" alt="image-20201223161944059" style="zoom: 50%;" />
如圖所示,John Smith 和 Sandra Dee 發生了哈希沖突,都被計算到 152 號桶,于是 Sandra 就去了下一個空位 - 153 號桶,當然也會對之后的 key 發生影響:Ted Baker 計算結果本應是放在 153 號的,但鑒于已經被 Sandra 占了,就只能再去下一個空位了,所以到了 154 號。
這種方式叫做 Linear probing 線性探查,就像上圖所示,一個個的順著找下一個空位。當然還有其他的方式,比如去找平方數,或者 Double hashing.
### 2.7 ConcurrentHashMap
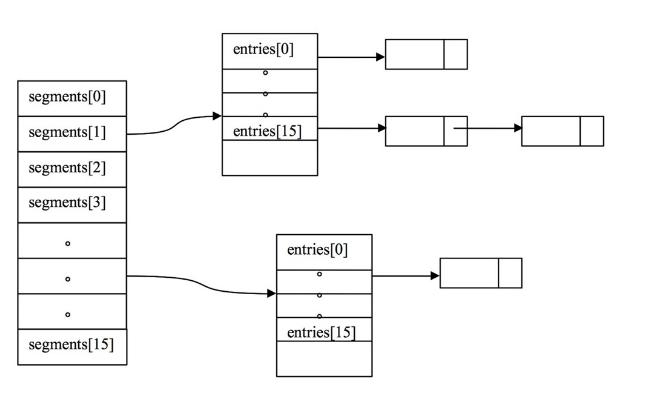
一個 ConcurrentHashMap 維護一個 Segment 數組,一個 Segment 維護一
個 HashEntry 數組。
**Segment 段**
ConcurrentHashMap 和 HashMap 思路是差不多的,但是因為它支持并發操作,所以要復雜一些。整個 ConcurrentHashMap 由一個個 Segment 組成, Segment 代表”部分“或”一段“的意思,所以很多地方都會將其描述為分段鎖。注意,行文中,我很多地方用了“槽”來代表一個segment。
**線程安全(Segment 繼承 ReentrantLock 加鎖)**
簡單理解就是, ConcurrentHashMap 是一個 Segment 數組, Segment 通過繼承ReentrantLock 來進行加鎖,所以每次需要加鎖的操作鎖住的是一個 segment,這樣只要保證每個 Segment 是線程安全的,也就實現了全局的線程安全
#### 2.7.1 JDK1.7 ConCurrentHashMap 原理
其中 Segment 繼承于 ReentrantLock
<img src="https://i.loli.net/2020/12/23/sYorGxkKfiHgZty.png" alt="image-20201223162327891" style="zoom:50%;" />
**并行度(默認 16)**
concurrencyLevel:并行級別、并發數、 Segment 數,怎么翻譯不重要,理解它。默認是 16,也就是說 ConcurrentHashMap 有 16 個 Segments,所以理論上, 這個時候,最多可以同時支持 16 個線程并發寫,只要它們的操作分別分布在不同的 Segment 上。這個值可以在初始化的時候設置為其他值,但是一旦初始化以后,它是不可以擴容的。再具體到每個 Segment 內部,其實每個 Segment 很像之前介紹的 HashMap,不過它要保證線程安全,所以處理起來要麻煩些.


Segment 繼承了 ReentrantLock,表明每個 segment 都可以當做一個鎖。這樣對每個 segment 中的數據需要同步操作的話都是使用每個 segment 容器對象自身的鎖來實現。只有對全局需要改變時鎖定的是所有的 segment。

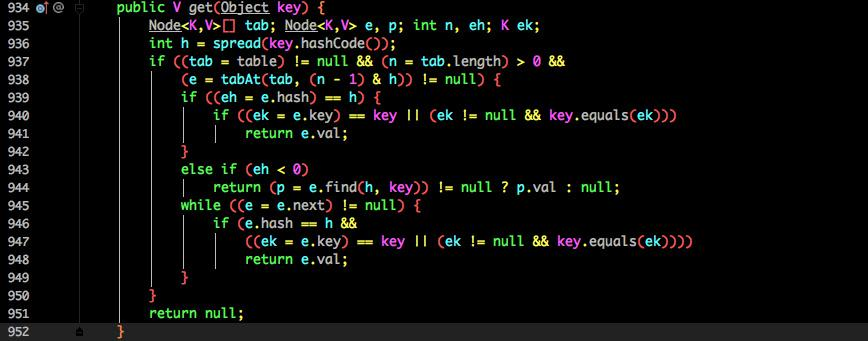
#### 2.7.2 JDK1.7 Get

**CurrentHashMap 是否使用了鎖???**
它也沒有使用鎖來同步,只是判斷獲取的 entry 的 value 是否為 null,為null 時才使用加鎖的方式再次去獲取。 這里可以看出并沒有使用鎖,但是value 的值為 null 時候才是使用了加鎖!!!
**Get 原理:**
第一步,先判斷一下 count != 0;count 變量表示 segment 中存在 entry的個數。如果為 0 就不用找了。假設這個時候恰好另一個線程 put 或者 remove了這個 segment 中的一個 entry,會不會導致兩個線程看到的 count 值不一致呢?看一下 count 變量的定義: transient volatile int count;它使用了 volatile 來修改。我們前文說過,Java5 之后,JMM 實現了對 volatile的保證:對 volatile 域的寫入操作 happens-before 于每一個后續對同一個域
的讀寫操作。所以,每次判斷 count 變量的時候,即使恰好其他線程改變了
segment 也會體現出來

- **1) 在 get 代碼的①和②之間,另一個線程新增了一個 entry**
如果另一個線程新增的這個 entry 又恰好是我們要 get 的,這事兒就比較微妙了。下圖大致描述了 put 一個新的 entry 的過程。
<img src="https://i.loli.net/2020/12/24/wCiepaL7SAHEG2y.png" alt="image-20201224093427997" style="zoom:67%;" />
因為每個 HashEntry 中的 next 也是 final 的,沒法對鏈表最后一個元素增加一個后續 entry 所以新增一個 entry 的實現方式只能通過頭結點來插入了。newEntry 對象是通過 new HashEntry(K k , V v, HashEntry next) 來創建的。如果另一個線程剛好 new 這個對象時,當前線程來 get 它。因為沒有同步,就可能會出現當前線程得到的newEntry 對象是一個沒有完全構造好的對象引用。 如果在這個 new 的對象的后面,則完全不影響,如果剛好是這個 new的對象,那么當剛好這個對象沒有完全構造好,也就是說這個對象的 value 值為 null,就出現了如下所示的代碼,需要重新加鎖再次讀取這個值!

- **2) 在 get 代碼的①和②之間,另一個線程修改了一個 entry 的 value**
value 是用 volitale 修飾的,可以保證讀取時獲取到的是修改后的值。
- **3) 在 get 代碼的①之后,另一個線程刪除了一個 entry**
假設我們的鏈表元素是:e1-> e2 -> e3 -> e4 我們要刪除 e3 這個 entry,因為 HashEntry 中 next 的不可變,所以我們無法直接把 e2 的 next 指向 e4,而是將要刪除的節點之前的節點復制一份,形成新的鏈表。它的實現大致如下圖所示:
<img src="https://i.loli.net/2020/12/24/2zBZMuOjDNY7edX.png" alt="image-20201224093637324" style="zoom:67%;" />
如果我們 get 的也恰巧是 e3,可能我們順著鏈表剛找到 e1,這時另一個線程就執行了刪除 e3 的操作,而我們線程還會繼續沿著舊的鏈表找到 e3 返回。這里沒有辦法實時保證了,也就是說沒辦法看到最新的。
我們第①處就判斷了 count 變量,它保障了在 ①處能看到其他線程修改后的。①之后到②之間,如果再次發生了其他線程再刪除了 entry 節點,就沒法保證看到最新的了,這時候的 get 的實際上是未更新過的!!!。
不過這也沒什么關系,即使我們返回 e3 的時候,它被其他線程刪除了,暴漏出去的 e3 也不會對我們新的鏈表造成影響。
#### 2.7.3 JDK1.7 Put
1. 將當前 Segment 中的 table 通過 key 的 hashcode 定位到 HashEntry。
2. 遍歷該 HashEntry,如果不為空則判斷傳入的 key 和當前遍歷的 key 是否相等,相等則覆蓋舊的 value。
3. 不為空則需要新建一個 HashEntry 并加入到 Segment 中,同時會先判斷是否需要擴容。
4. 最后會解除在 1 中所獲取當前 Segment 的鎖。
可以說是首先找到segment,確定是哪一個segment,然后在這個 segment中遍歷查找 key值是要查找的key值得entry,如果找到,那么就修改該key,如果沒找到,那么就在頭部新加一個 entry.

#### 2.7.4 JDK1.7 Remove

<img src="https://i.loli.net/2020/12/24/DtOobZRdF9qPAvU.png" alt="image-20201224094626707" style="zoom:67%;" />
#### 2.7.5 JDK1.8 ConCurrentHashMap原理
1. 其中拋棄了原有的 其中拋棄了原有的 Segment 分段鎖,而采用了 分段鎖,而采用了CAS + synchronized 來保證并發安全性。
2. 大于 大于 8 的時候才去紅黑樹 的時候才去紅黑樹鏈表轉紅黑樹的閥值,當 鏈表轉紅黑樹的閥值,當 table[i]下面的鏈表長度 下面的鏈表長度大于 大于 8時就轉化為紅黑樹結構。
**Java8 實現 (引入了紅黑樹)**
<img src="https://i.loli.net/2020/12/23/gRh41vz6en2aAfE.png" alt="image-20201223162435125" style="zoom: 50%;" />
#### 2.7.6 JDK1.8 get
- 根據計算出來的 hashcode 尋址,如果就在桶上那么直接返回值。
- 如果是紅黑樹那就按照樹的方式獲取值。
- 就不滿足那就按照鏈表的方式遍歷獲取值
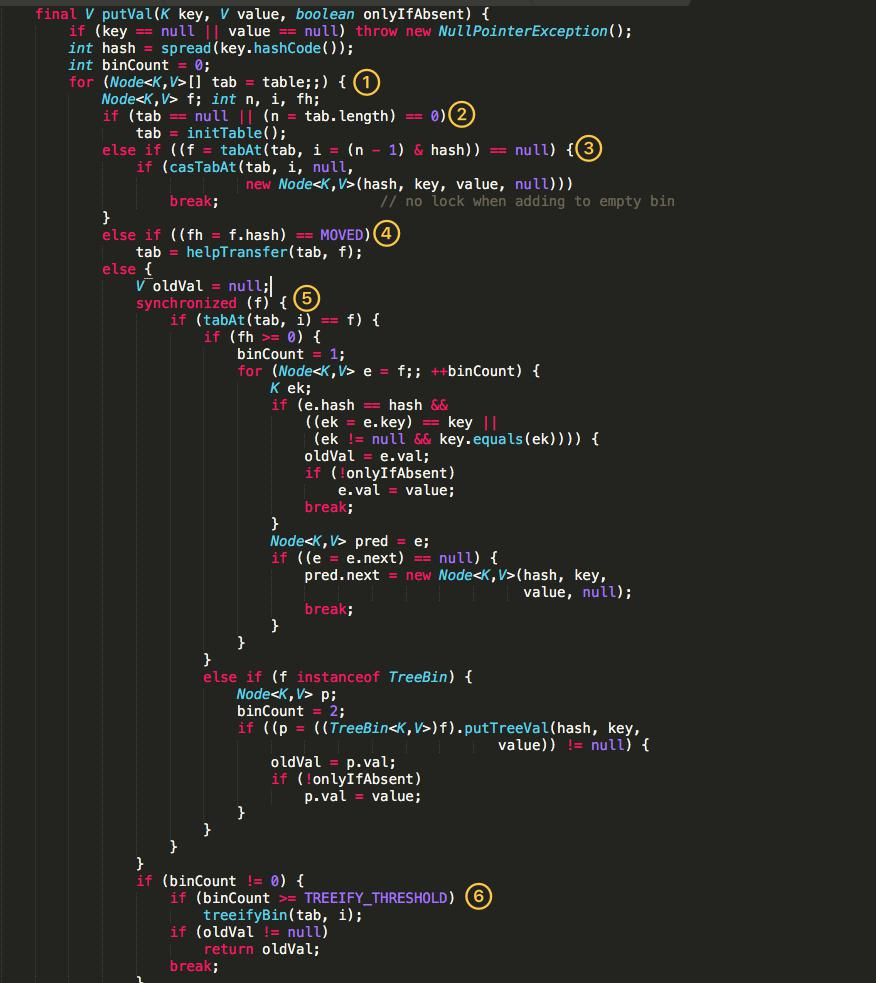
#### 2.7.7 JDK1.8 Put
- 根據 key 計算出 hashcode 。
- 判斷是否需要進行初始化
- f 即為當前 key 定位出的 Node,如果為空表示當前位置可以寫入數據,利用 CAS
嘗試寫入,失敗則自旋保證成功。
- 如果當前位置的 hashcode == MOVED == -1,則需要進行擴容。
- 如果都不滿足,則利用 synchronized 鎖寫入數據(分為鏈表寫入和紅黑樹寫入)。
- 如果數量大于 TREEIFY_THRESHOLD 則要轉換為紅黑樹。
#### 2.7.8 HashTable HashMap ConCurrentHashMap區別
**hashtable 和hashmap 區別**
- Hashtable的方法是同步的, HashMap未經同步,所以在多線程場合要手動同步。
- Hashtable不允許null值(key和vlue都不可以), HashMap允許h值(key和value都可以)
- 兩者的遍歷方式大同小異, Hashtable僅僅比 HashMap多一個 elements方法。
- Hashtable和 HashMap都能通過 values()方法返回一個 Collection,然后進行遍歷處理。
- 兩者也都可以通過 entry Set()方法返回一個set,然后進行遍歷處理
- HashTable使用 Enumeration, HashMap使用 Iterator
- 哈希值使用不同, Hashtable直接使用對象的 hashCode。而 HashMap重新計箅hash,而且用于代替求模。
- H-ashtable中hash數組默認大小是11,增加的方式是od*2+1. HashMap中hash數組的默認大小是16,而且一定是2的指數
- HashTable基于 Dictionary類,而 HashMap基于 AbstractMap類
**HashMap 和 和 ConCurrentHashMap 區別**
- HashMap是非線程安全的, ConCurrentHashMap是線程安全的
- ConCurrentHashMap將整個Hash桶進行了分段 segment,也就是將這個大的數組分成了幾個小的片段 segment,而且毎個小的片段 segment上面有鎖存在,那么在插入元素的時候就需要先找到應該插入到哪一個片段 segment,然后再在這個片段上面進行插入,而且這里還齋要獲取 segment鎖
- ConcurmentHashMap讓鎖的拉度更精細些,并發性能更好。
**ConcurrentHashMap 和 HashTable 區別**
<img src="https://i.loli.net/2020/12/24/C6Ua3xOc7VGPNdL.png" alt="image-20201224102022411" style="zoom: 50%;" />
### 2.8 LinkedHashMap
>LinkedHashMap 繼承自 HashMap,在 HashMap 基礎上,通過維護一條**雙向鏈表**,解決了 HashMap 不能隨時保持**遍歷順序**和**插入順序**一致的問題。除此之外,LinkedHashMap 對**訪問順序**(LRU)也提供了相關支持。在一些場景下,該特性很有用,比如緩存。
<img src="https://i.loli.net/2020/02/01/UK5B6SGw94MlgI3.jpg" alt="-w500" style="zoom:50%;" />
* 繼承自 HashMap,因此具有和 HashMap 一樣的快速查找特性。
```java
public class LinkedHashMap<K,V>
extends HashMap<K,V> implements Map<K,V>
```
內部維護了一個`雙向鏈表`,用來維護**插入順序**或者 **LRU 順序**。
*accessOrder 決定了順序,默認為 false,此時維護的是插入順序。初始化為true則為訪問順序*
```java
final boolean accessOrder;
```
LinkedHashMap 最重要的是以下用于維護順序的函數,它們會在 put、get 等方法中調用。
```java
void afterNodeAccess(Node<K,V> p) { }
void afterNodeInsertion(boolean evict) { }
void afterNodeRemoval(Node<K,V> p) { }
```
#### 2.7.1 afterNodeAccess()訪問后的處理
當一個節點被訪問時,如果 **accessOrder 為 true**(*即它按訪問順序維護鏈表)*,則會將該節點移到鏈表尾部。也就是說指定為 LRU 順序之后,在每次訪問一個節點時,會將這個節點移到鏈表尾部,保證鏈表尾部是最近訪問的節點,那么鏈表首部就是最近最久未使用的節點。
```java
// 如果 accessOrder 為 true,
//則調用 afterNodeAccess 將被訪問節點移動到鏈表最后
if (accessOrder)
afterNodeAccess(e);
```
假設我們訪問下圖鍵值為3的節點,訪問前結構為:
<img src="https://i.loli.net/2020/02/01/uOJ6Y4znKy1TCx8.jpg" alt="-w500" style="zoom: 50%;" />
訪問后,鍵值為3的節點將會被移動到雙向鏈表的最后位置,其前驅和后繼也會跟著更新。訪問后的結構如下
<img src="https://i.loli.net/2020/02/01/yhxHFNZKTnVJB6W.jpg" alt="-w500" style="zoom:50%;" />
#### 2.7.2 afterNodeRemoval()刪除后的處理
刪除的過程并不復雜,上面這么多代碼其實就做了三件事:
- 根據 hash 定位到桶位置
- 遍歷鏈表或調用紅黑樹相關的刪除方法
- 從 LinkedHashMap 維護的雙鏈表中移除要刪除的節點
<img src="https://i.loli.net/2020/02/01/q4xYiMfKhXP2HyI.jpg" alt="-w500" style="zoom:50%;" />
根據 hash 定位到該節點屬于3號桶,然后在對3號桶保存的單鏈表進行遍歷。找到要刪除的節點后,先從單鏈表中移除該節點。如下:
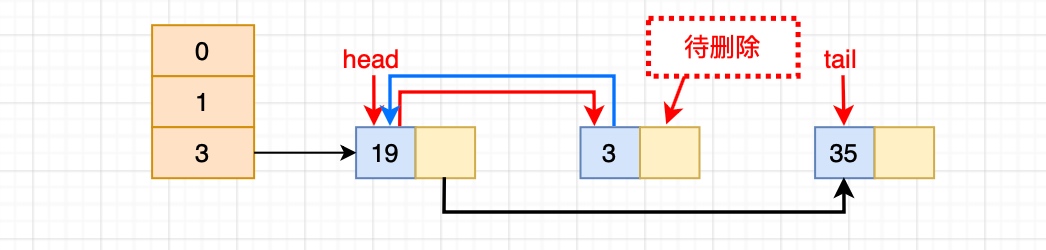
然后再雙向鏈表中移除該節點:
<img src="https://i.loli.net/2020/02/01/UvEDkdCButhQwgF.jpg" alt="-w500" style="zoom:50%;" />
#### 2.7.3 afterNodeInsertion()
在 put 等操作之后執行,當 `removeEldestEntry()` 方法返回 true 時會移除最晚的節點,也就是鏈表首部節點 first。
`removeEldestEntry()`(可以用來判斷節點是否超限) 默認為 false,如果需要讓它為 true,需要繼承 `LinkedHashMap` 并且覆蓋這個方法的實現,這在實現 LRU 的緩存中特別有用,通過移除最近最久未使用的節點,從而保證緩存空間足夠,并且緩存的數據都是熱點數據。
```java
void afterNodeInsertion(boolean evict){
LinkedHashMap.Entry<K,V> first;
// 根據條件判斷是否移除最近最少被訪問的節點
if (evict && (first = head) != null && removeEldestEntry(first)) {
K key = first.key;
removeNode(hash(key), key, null, false, true);
}
}
// 移除最近最少被訪問條件之一,通過覆蓋此方法可實現不同策略的緩存
protected boolean removeEldestEntry(Map.Entry<K,V> eldest) {
return false;
}
```
>參考:
>【LinkedHashMap 源碼詳細分析(JDK1.8)】https://www.imooc.com/article/22931
#### 2.7.4 LRU 緩存
以下是使用 LinkedHashMap 實現的一個 LRU 緩存:
* 設定最大緩存空間 MAX_ENTRIES 為 3;
* 使用 LinkedHashMap 的構造函數將 accessOrder 設置為 true,開啟 LRU 順序;
* 覆蓋 removeEldestEntry() 方法實現,在節點多于 MAX_ENTRIES 就會將最近最久未使用的數據移除
```java
class LRUCache<K, V> extends LinkedHashMap<K, V> {
private static final int MAX_ENTRIES = 3;
protected boolean removeEldestEntry(Map.Entry eldest) {
return size() > MAX_ENTRIES;
}
LRUCache() {
super(MAX_ENTRIES, 0.75f, true);
}
}
public static void main(String[] args) {
LRUCache<Integer, String> cache = new LRUCache<>();
cache.put(1, "a");
cache.put(2, "b");//本例中最早且非最近使用
cache.put(3, "c");
cache.get(1);//最近使用
cache.put(4, "d");
System.out.println(cache.keySet());//[3, 1, 4]
}
```
### 2.9 WeakHashMap
#### 2.9.1 存儲結構
`WeakHashMap `的 **Entry** 繼承自 WeakReference,被 WeakReference 關聯的對象在**下一次垃圾回收**時會被回收。
WeakHashMap 主要用來*實現緩存*,通過使用 WeakHashMap 來引用緩存對象,由 JVM 對這部分緩存進行回收。
```java
private static class Entry<K,V>
extends WeakReference<Object> implements Map.Entry<K,V>
```
這個“弱鍵”的原理呢?大致上就是,通過**WeakReference**和**ReferenceQueue**實現的。 `WeakHashMap`的*key*是“弱鍵”,即是WeakReference類型的;**ReferenceQueue**是一個隊列,它會保存被GC回收的“弱鍵”。
實現步驟是:
- (01) 新建WeakHashMap,將“**鍵值對**”添加到WeakHashMap中。實際上,WeakHashMap是通過數組table保存Entry(鍵值對);每一個Entry實際上是一個單向鏈表,即Entry是鍵值對鏈表。
- (02) 當**某“弱鍵”不再被其它對象引用**,并**被GC回收**時。在GC回收該“弱鍵”時,**這個“弱鍵”也同時會被添加到ReferenceQueue(queue)隊列**中。
- (03) 當下一次我們需要操作WeakHashMap時,會先同步table和queue。table中保存了全部的鍵值對,而queue中保存被GC回收的鍵值對;同步它們,就是**刪除table中被GC回收的鍵值對**。
#### 2.9.2 ConcurrentCache
Tomcat 中的 **ConcurrentCache** 使用了 *WeakHashMap* 來實現緩存功能。
ConcurrentCache 采取的是分代緩存:
* **經常使用**的對象放入 eden 中,**eden** 使用 *ConcurrentHashMap* 實現,不用擔心會被回收(伊甸園);
* **不常用的**對象放入 **longterm**,longterm 使用 *WeakHashMap* 實現,這些老對象會被垃圾收集器回收。
* 當調用 `get()` 方法時,會先從 eden 區獲取,如果沒有找到的話再到 longterm 獲取,當從 longterm 獲取到就把對象放入 eden 中,從而保證經常被訪問的節點不容易被回收。
* 當調用 `put()` 方法時,如果 eden 的大小超過了 size,那么就將 eden 中的所有對象都放入 longterm 中,利用虛擬機回收掉一部分不經常使用的對象。
### 2.10 PriorityQueue
>PriorityQueue 是一個基于優先級堆的無界隊列,它的元素都以他們的自然順序有序排列。Java中的PriorityQueue采用的是堆這種數據結構來實現的,而存儲堆采用的則是數組。
**滿二叉樹**
二叉樹當中,葉子節點全部在最底層除了葉子節點外,每個節點都有左右兩個子節點
<img src="https://i.loli.net/2020/02/02/PzhCfFqpEkiNKRu.jpg" alt="-w200" style="zoom:50%;" />
**完全二叉樹**
如果葉子節點都在最底下兩層,最后一層的葉子節點都靠左排列,并且除了最后一層,其他層的節點個數都要達到最大,這種二叉樹就叫作完全二叉樹
<img src="https://i.loli.net/2020/02/02/8MJjqGkHblZQzcR.jpg" alt="-w400" style="zoom:50%;" />
`堆`是一個**完全二叉樹**,堆中每一個節點的值都必須大于等于(或小于等于)其子樹中每個節點的值。
- 對于每個節點的值**都大于等于**子樹中每個節點值的堆,我們叫做`大頂堆`。
- 對于每個節點的值**都小于等于**子樹中每個節點值的堆,我們叫做`小頂堆`。
**PriorityQueue的特點:**
>- 1. PriorityQueue 是基于*堆*的,堆是一個特殊的*完全二叉樹*,它的每一個節點的值都必須小于等于(或大于等于)其子樹中每個節點的值
- 2. PriorityQueue 的**出隊**和**入隊**操作時間復雜度都是 *O(log(n))*,僅與堆的高度有關
- 3. PriorityQueue 初始容量為 11,支持**動態擴容**。容量小于 64 時,擴容一倍。大于 64 時,擴容 0.5 倍
- 4. PriorityQueue **不允許 null** 元素,*不允許不可比較的元素*
- 5. PriorityQueue **不是線程安全**的,PriorityBlockingQueue **是線程安全的**
#### 2.10.1 如何實現一個堆
<img src="https://i.loli.net/2020/02/02/YzVTlqLPtIgfWiy.jpg" alt="-w400" style="zoom:50%;" />
可以看出來,數組中下標為i的節點,其左子節點就是下標為 i*2+1 的節點,右子節點則是下標為 i*2+2 的節點。
PriorityQueue數據結構如下:
```java
public class PriorityQueue<E> extends AbstractQueue<E>
implements java.io.Serializable {
private static final int DEFAULT_INITIAL_CAPACITY = 11;
// 數組
transient Object[] queue;
// 數組中元素個數
private int size = 0;
}
```
#### 2.10.2 新增
新增的時候,我們將插入的數據暫時放置到數組中的**最后一個位置**,運氣好的話,它就剛好滿足堆特性,也不需要移動元素了。不好的話就需要移動元素位置了。
移動過程如下:**新插入**的節點與*父節點*比較大小,如果不滿足子節點大于等于父節點的大小關系(小頂堆),則*互換*兩個節點,一直*重復*這個過程,直到父子節點滿足剛才說的那種關系

```java
/*
1.判斷插入元素是否為空,為空則拋出NPE異常
2.在判斷數組是否需要擴容,如果是則進行擴容
3.如果是第一次插入元素,則放入數組的第一個位置
4.如果不是則進行堆化過程
4.1 找到父節點位置 : (k-1) >>> 1
4.2 判斷插入元素的值是否大于父節點(小頂堆),如果是則結束堆化過程
4.3 如果不是則交換元素位置
4.4 持續上面的1,2,3步驟,直到插入的節點已經是堆頂結點(k==0)
*/
public boolean offer(E e) {
if (e == null) throw new NullPointerException();
modCount++;
int i = size;
if (i >= queue.length) grow(i + 1);
size = i + 1;
// 第一次插入放入數組的第一個位置(下標從0開始)
if (i == 0) queue[0] = e;
else siftUp(i, e);
return true;
}
// 堆化過程
private void siftUpComparable(int k, E x) {
Comparable<? super E> key = (Comparable<? super E>) x;
while (k > 0) {
// 1. 父節點位置 (k-1)/2,這里采用無符號右移(值為整數)
int parent = (k - 1) >>> 1;
Object e = queue[parent];
// 2. 如果要插入的元素大于父節點元素的值,則結束堆化過程
if (key.compareTo((E) e) >= 0)
break;
// 3. 交換元素位置
queue[k] = e;
k = parent;
}
queue[k] = key;
}
```
#### 2.10.3 刪除
對于小頂堆而言,當刪除堆頂元素之后,就需要把第二小的元素放到堆頂,那么第二小的元素就會出現在左右子節點中。
當刪除后,如果我們還是迭代的從左右子節點中選擇最小元素放入堆頂,就會造成數組空洞,我用下面的圖來演示這個問題。

由于刪除了一個元素,所以在移動的過程中會導致空洞,所以要找一個元素把這個洞填起來呢?我們可以在刪除堆頂元素的時候,將最后一個元素拿來補位。由于在堆化的過程中,都是交換操作,就不會出現數組空洞了。
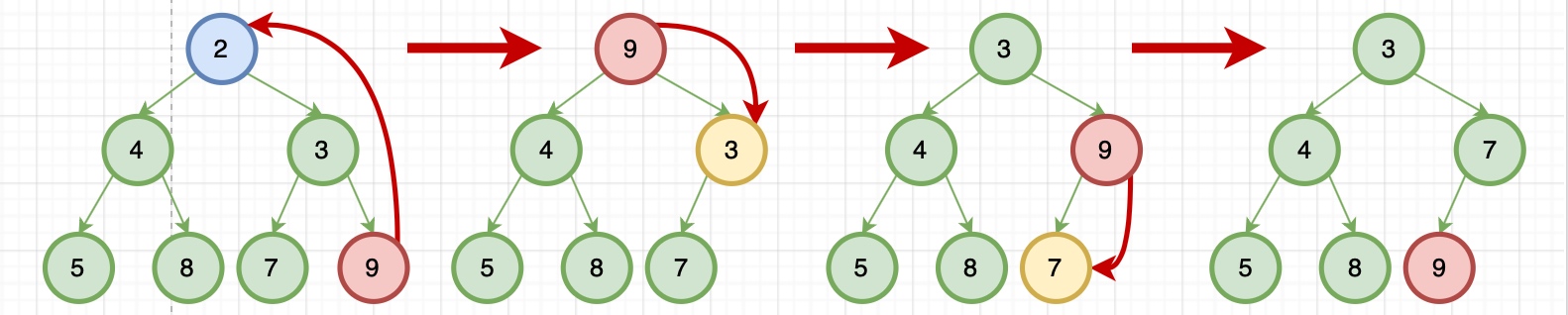
```java
// k=0, x=queue[size-1]
private void siftDownComparable(int k, E x) {
Comparable<? super E> key = (Comparable<? super E>)x;
int half = size >>> 1; // loop while a non-leaf
while (k < half) {
int child = (k << 1) + 1; // assume left child is least
// 找到左右子節點中小的那個節點
Object c = queue[child];
int right = child + 1;
if (right < size &&
((Comparable<? super E>) c).compareTo((E) queue[right]) > 0)
c = queue[child = right];
// 如果比小的那個節點值還要小,則循環結束
if (key.compareTo((E) c) <= 0)
break;
// 移動數據
queue[k] = c;
k = child;
}
queue[k] = key;
}
```
需要注意的是這里的結束條件是k < half,為什么呢?因為我們的堆化是從上到下,只會找一邊(要么是左子樹,要么是右子樹)。
>參考
>https://mp.weixin.qq.com/s/mJbzq1kMs8SpW7baCHUqRA
>https://mp.weixin.qq.com/s/JosUVtCnxs49DWIOD0056g
### 2.11 AVL(平衡二叉搜索樹)
#### 2.11.1 二叉搜索樹復雜度分析
二叉搜索樹退化成鏈表
- 當n比較大時,兩者的性能差異比較大
- 比如當n=1000000時,二叉搜素樹的最低高度是20

除了添加會退化成鏈表以為,多次刪除操作也會使其退化

平衡二叉搜索樹的出現就是為了防止二叉搜索樹退化成鏈表,使其的操作復雜度維持在$O(log_2N)$
**平衡的概念**
當節點數量固定時,左右子樹的高度越接近,這顆二叉樹就越平衡(樹的高度越低)
如下:同樣節點的二叉樹,從左到右的平衡性越來越好

最理想的平衡,就是像完全二叉樹、滿二叉樹那些,高度最小
#### 2.11.2 平衡二叉搜索樹(Balanced Binary search Tree )
也稱自平衡二叉搜索樹,英文簡稱BBST,經典常見的平衡二叉搜索樹有
- AVL樹 :windows NT內核中廣泛使用
- 紅黑樹:
- C++ STL(比如map,set)
- JAVA的TreeMap,TreeSet,HashMap,HashSet
- Linux進程調度
- Nigx的timer管理
#### 2.11.3 AVL樹
- 平衡因子(Balance Factor):某節點左右子樹的高度差
- AVL樹的特點
- 每個節點的平衡因子只可能是1、0、-1(絕對值小于1,如果超過1,稱之為“失衡”)
- 每個節點的左右子樹高度差不超過1
- 搜索、添加、刪除的時間復雜度是$O(log_2N)$

**添加導致的失衡**

**LL-右旋轉(單旋)**
旋轉之后仍然是一個二叉搜索樹:T0 < n < T1 < p < T2 < g < T3,整棵樹再次平衡(仔細觀察,旋轉之后,高度又回到紅線上面,說明子部分的樹高度沒有變化,原來全樹整體再次平衡)選擇后續工作:更新g,p高度,更新T2,p,g的parent指向。

**RR-左旋轉(單旋)**
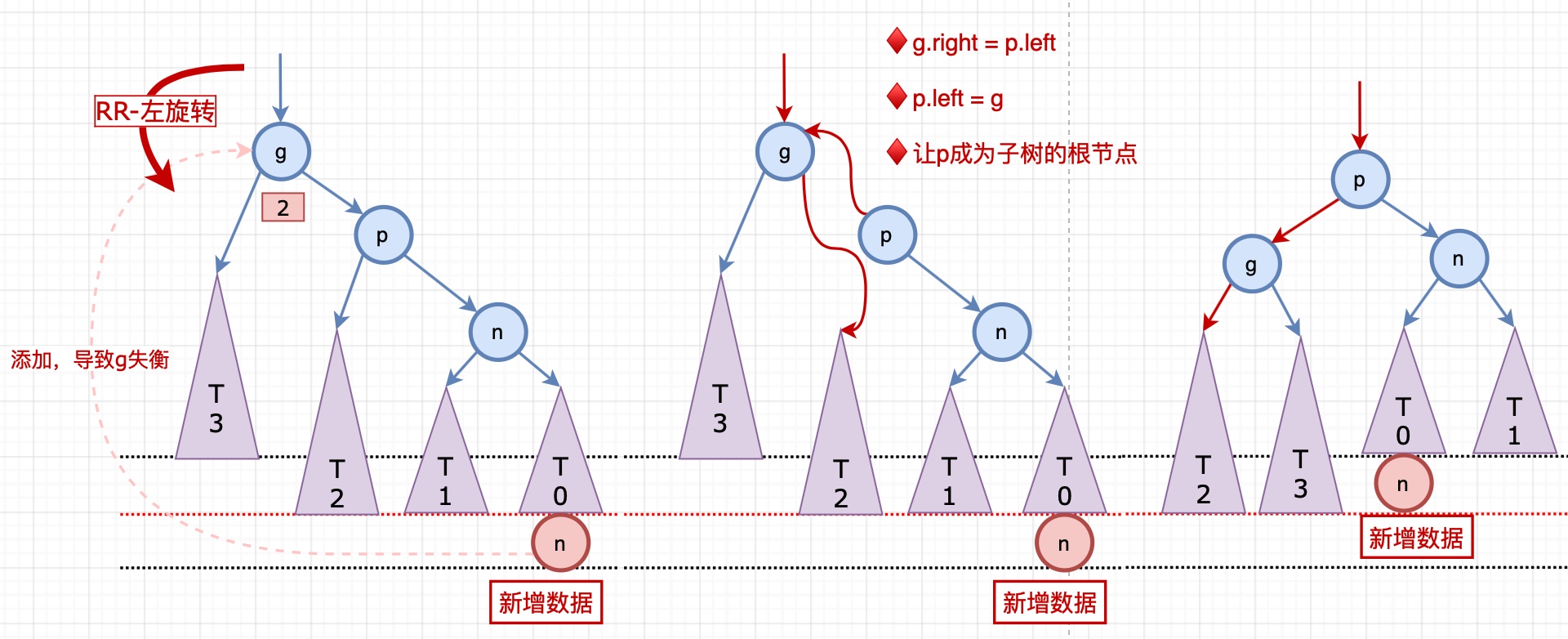
**LR-RR左旋轉,LL右旋轉(雙旋轉)**

**RL-LL右旋轉,RR左旋轉**

》https://www.bilibili.com/video/av77758248?p=51
### 2.12 2-3樹
2-3樹和紅黑樹有一定的聯系,對于理解紅黑樹會有很大的幫助,所以我們先來看一下2-3樹相關的一些性質。首先,2-3樹滿足二分搜索樹的性質。不同的是在2-3樹中,存在兩種節點。一種是有兩個葉子節點的,我們稱作“2節點”;另一種是有三個葉子節點的,我們稱作“3節點”。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/2-3樹節點概覽.png" alt="img" style="zoom:33%;" />
如下是一整顆2-3樹的示例。需要強調的是2-3樹是完全平衡的樹,即從根節點到任意一個葉子節點的高度都是相同的。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/2-3樹整體示例.png" alt="img" style="zoom:33%;" />
**2-3樹怎樣保持完全平衡性**
向2-3樹中添加一個節點,遵循向二分搜索樹中添加節點的基本思路,插入節點比當前節點小,則向當前節點的左子樹添加,否則向右子樹添加。不過由于2-3樹特殊的性質,當要向“2節點”添加節點時,將待插入的節點與該“2節點”進行融合,組成一個新的“3節點”,如下圖所示。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/2-3樹插入2節點.png" alt="img" style="zoom:33%;" />
如果要向“3節點”添加節點,同向“2節點”添加節點一樣,先組成一個臨時的4節點,之后再拆分成3個“2節點”,如圖所示。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/2-3樹插入3節點.png" alt="img" style="zoom:33%;" />
如果要插入的“3節點”的父節點是一個“2節點”,通過上述步驟得到的拆分過成為父節點的“2節點”,需要向原“3節點”的父節點進行融合,組成新的“3節點”。過程如下圖所示。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/2-3樹插入3節點-父節點.png" alt="img" style="zoom:33%;" />
如果要插入的“3節點”的父節點是一個“3節點”,大體思路相同,向父節點進行融合,只不過此時融合后成為一個臨時的“4節點”,之后要再次進行拆分。過程如圖所示。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/2-3樹插入3節點-父節點3.png" alt="img" style="zoom: 33%;" />
如上所述,2-3樹保持了完全的平衡性。說了這么長時間的2-3樹,那么2-3樹和紅黑樹之間到底有怎樣的關系,下面我們具體來看一下。
#### 2-3樹與紅黑樹
對于2-3樹中的“2節點”,對應于紅黑樹中的“黑節點”,即相當于普通二分搜索樹中的一個節點。
對于2-3樹中的“3節點”,相當于普通二分搜索樹中的兩個節點融合在一起,我們如何來描述這種融合在一起的兩個節點之間的關系呢?其實很簡單,如果我們將連接這兩個節點的邊涂成紅色,就可以表示這兩個節點是融合的關系,即2-3樹中的一個“3節點”。那么問題又來了,對于樹這種數據結構,我們在定義的時候通常都是針對節點進行定義,并沒有對節點之間的邊進行定義,我們如何來表示這條被涂成紅色的邊呢?大家都知道,對于樹中的任意一個節點,都是只有一個父親節點,所以與其父節點相連接的邊可以用該節點進行表示。那么我們就可以將這兩個節點中較小的節點(作為左子樹的節點)涂成紅色,就可以很好地表示這兩個節點融合的關系了。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/2-3樹與紅黑樹-3節點對應.png" alt="img" style="zoom:33%;" />
綜合以上描述,2-3樹與紅黑樹之間的關系,我們可以用下圖很好地進行表示。我們這里說的紅色節點都是向左傾斜的。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/2-3樹與紅黑樹-節點綜合.png" alt="img" style="zoom:33%;" />
看過2-3樹中的兩種節點和紅黑樹中節點的對應關系后,我們就來看一下一棵2-3樹與紅黑樹之間的對比,如圖所示。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/2-3樹與紅黑樹-整體對比.png" alt="img" style="zoom:33%;" />
### 2.14 紅黑樹
#### 2.14.1 紅黑樹的性質
1. 每個節點或者是紅色,或者是黑色
2. 根節點是黑色
3. 每一個葉子節點(最后的空節點)是黑色的
4. 如果一個節點是紅色的,那么它的孩子節點都是黑色的
5. 從任意一個節點到葉子節點,經過的黑色節點是一樣的
>1. 每個節點或者是紅色,或者是黑色
> 這條定義很好理解,在此不做解釋。
>2. 根節點是黑色
> 根據之前說過的,紅色的節點對應于2-3樹中“3節點”中較小的那個節點,拆成兩個“2節點”的話則是一個左子樹的節點,即紅色的節點總是可以和其父節點進行融合,所以紅色節點一定有父節點,顯然根節點不能是紅色,所以根節點是黑色。
>3. 每一個葉子節點(最后的空節點)是黑色的
> 這條性質和第2條是對應的。對于葉子節點(最后的空節點),一顆空樹的根節點也為黑色,所以與其說第三條是一條性質,不如說也是一個定義。
>4. 如果一個節點是紅色的,那么它的孩子節點都是黑色的
> 根據上面2-3樹與紅黑樹兩種節點的對比圖,我們很容易看到,紅色節點的兩個子樹,對應2-3樹中的話,要么是一個“2節點”,要么是一個“3節點”,而不管是“2節點”還是“3節點”,相連的第一個節點都是黑色的,所以說紅色節點的孩子節點都是黑色的。
>5. 從任意一個節點到葉子節點,經過的黑色節點是一樣的
> 根據2-3樹與紅黑樹的關系對比圖,可以發現,紅黑樹中一個黑色節點對應2-3樹中一整個節點(“2節點”或“3節點”),而2-3樹是完全平衡的樹,從根節點到任意路徑的葉子節點,經過的節點個數都是相同的,對應紅黑樹中,即從任意節點到葉子節點,經過的黑色節點是一樣的。
#### 2.14.2 紅黑樹添加元素
回憶剛剛提到的向2-3樹中添加元素的過程,或者添加進一個“2節點”,形成一個“3節點”,或者添加進一個“3節點”,形成一個臨時的“4節點”。理解了2-3樹如何添加節點,對應紅黑樹就很好理解了。很容易知道,我們總是會將待插入的節點向父節點進行融合,所以我們將待插入的節點看成紅色,即永遠添加紅色節點。
向一棵空樹添加節點42。插入后,該節點是根節點,根據紅黑樹的性質,根節點必須是黑色,所以講該節點染成黑色。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹添加-根節點.png" alt="img" style="zoom:33%;" />
若向如圖的紅黑樹中添加節點37。因為37比42小,所以添加在42的左子樹,對應2-3樹中,形成一個“3節點”
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹添加-左子樹.png" alt="img" style="zoom:33%;" />
若向如圖的紅黑樹中添加節點42。因為42比37大,所以添加在37的右子樹。這樣的話紅色節點就出現在了一個節點的右子樹中,所以此時需要進行左旋轉,讓樹滿足紅黑樹的性質。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹添加-左旋轉.png" alt="img" style="zoom:33%;" />
##### 2.14.2.1 左旋轉
對于一般的情況,如何進行左旋轉呢?我們要對下圖的紅黑樹進行左旋轉。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/左旋轉-初始.png" alt="img" style="zoom:33%;" />
首先將node節點與x節點斷開,其次將x的左子樹作為node的右子樹。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/左旋轉-過程1.png" alt="img" style="zoom:33%;" />
然后再將node作為x新的左子樹,之后要把x的顏色染成node的顏色,最后將node的顏色變為紅色,這樣就完成了左旋轉的操作。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/左旋轉-過程2.png" alt="img" style="zoom:33%;" />
##### 2.14.2.2 顏色翻轉(flipColors)
向紅黑樹中插入節點66,很容易知道插入到42右子樹的位置,對應于2-3樹的插入如圖所示。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/顏色翻轉-1.png" alt="img" style="zoom:33%;" />
然而上面我們說到,我們總是要將新拆分出來的樹的父親節點向上進行融合,即這個父親節點在紅黑樹中總是紅色的,根據紅黑樹的性質,該父親節點的兩個孩子節點一定是黑色的。這樣就需要將上一步形成的樹進行顏色的翻轉,變成如下圖的形態。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/顏色翻轉-2.png" alt="img" style="zoom:33%;" />
##### 2.14.2.3 右旋轉
向如圖的紅黑樹中插入節點12,根據二分搜索樹插入的操作,此時會形成一條鏈狀的結構,對于2-3樹中則是變形成為圖中的樣子,才能保證平衡性。所以在紅黑樹中,也要通過變形,變成與2-3樹對應的形態。這種情況的變形操作,稱為“右旋轉”。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/右旋轉-1.png" alt="img" style="zoom:33%;" />
一般的情況,右旋轉操作同上面的左旋轉操作很類似,下面我們一起來看一下過程。我們要對下圖的紅黑樹進行右旋轉的操作。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/右旋轉一般-初始.png" alt="img" style="zoom:33%;" />
首先將node和x節點斷開,將x的右子樹T1作為node的左子樹。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/右旋轉一般-過程1.png" alt="img" style="zoom:33%;" />
其次將node作為x的右子樹。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/右旋轉一般-過程2.png" alt="img" style="zoom:33%;" />
接著要把x的顏色染成原來node的顏色,把node染成紅色。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/右旋轉一般-過程3.png" alt="img" style="zoom:33%;" />
然后很顯然,需要再進行一次顏色翻轉操作,才能滿足紅黑樹的性質。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/右旋轉后顏色翻轉.png" alt="img" style="zoom:33%;" />
有一種比較復雜的情況,向下圖的紅黑樹中插入節點40,要滿足的紅黑樹的性質我們需要怎么操作呢?
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹插入復雜-1.png" alt="img" style="zoom:33%;" />
對應2-3樹中最終的形態,第一步我們可以通過一次左旋轉,變成下圖的樣子。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹插入復雜左旋轉.png" alt="img" style="zoom:33%;" />
會發現,這樣就變成了上面說到的需要右旋轉的形態,所以再進行一次右旋轉和顏色翻轉,就可以滿足紅黑樹的性質了。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹插入復雜右旋轉顏色翻轉.png" alt="img" style="zoom:33%;" />
##### 2.14.2.4 紅黑樹插入總結
上面分情況討論了向紅黑樹中添加節點的各種情況,這里總結一下。其實根據上面的討論,我們可以發現,最后一種復雜的情況可以涵蓋其余簡單的情況,復雜的操作包含了左旋轉、右旋轉、顏色翻轉,這三種操作,完全可以保持紅黑樹的性質。下面的一張圖,很好的總結了向紅黑樹中添加節點不同情況下的過程。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹插入總結.png" alt="img" style="zoom:33%;" />
#### 2.14.3 紅黑樹刪除元素
關于紅黑樹的刪除操作,比插入操作要復雜一些,需要分情況進行討論。下面我們具體來看一下。
紅黑樹的刪除操作大體分為2步:
1. 二分搜索樹刪除節點
2. 刪除修復操作
紅黑樹的刪除首先滿足二分搜索樹的刪除,然后對刪除節點后的樹進行修復操作,讓其重新滿足紅黑樹的5條性質。
對于二分搜索樹的刪除,這里就不再贅述,我們主要討論紅黑樹的刪除修復操作。以下所說的當前節點意思是通過二分搜索樹的方式刪除要刪除的節點后,代替原來節點的節點。
當刪除節點是紅色節點時,那么原來紅黑樹的性質依舊保持,此時不用做修復操作。
當刪除節點是黑色節點時,情況很多,我們分情況討論。
##### 2.14.3.1 簡單情況
1. 當前節點是紅色節點
直接把當前節點染成黑色,結束,紅黑樹的性質全部恢復。
2. 當前節點是黑色節點,并且是根節點
什么都不做,直接結束。
##### 2.14.3.2 復雜情況
###### 1.N、S、SL、SR、P都為黑色
其中N是上述的當前節點,S是N的兄弟節點,P是N的父節點,SL和SR是N兄弟節點的左右孩子節點。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹刪除情況1-1.png" alt="img" style="zoom:33%;" />
此時將S染成紅色,這樣經過N路徑的黑色節點就和N的兄弟子樹中的黑色節點相同了,但是經過P節點的黑色節點少了一個,此時需要將P當做新的N再進行操作,具體怎么操作可以見以下一些情況。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹刪除情況1-2.png" alt="img" style="zoom:33%;" />
###### 2.N、S、SL、SR為黑,P為紅
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹刪除情況2-1.png" alt="img" style="zoom:33%;" />
此時將P和S的顏色進行交換,P成為了黑色,它為經過節點N的路徑添加了一個黑色節點,從而補償了被刪除的黑色節點。S的顏色只是上移到父節點P上,因而經過S節點路徑的黑色節點的數目也沒有發生改變。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹刪除情況2-2.png" alt="img" style="zoom:33%;" />
###### 3.N、S為黑色,SR為紅色
圖中藍色節點表示該節點可以為黑色也可以為紅色,即對該節點的顏色沒有要求。
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹刪除情況3-1.png" alt="img" style="zoom:33%;" />
此時將以P為根的子樹進行左旋轉
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹刪除情況3-2.png" alt="img" style="zoom:33%;" />
然后交換P和S的顏色
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹刪除情況3-3.png" alt="img" style="zoom:33%;" />
將SR染成黑色
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹刪除情況3-4.png" alt="img" style="zoom:33%;" />
調整后經由N的路徑的黑色節點數比調整前增加了一個,恰好補償了被刪除的黑色節點。對于不經過N但經過其他節點的任意一個路徑來說,它們貢獻的黑色節點數目不變。
###### 4.N、S為黑,SL為紅,SR為黑
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹刪除情況4-1.png" alt="img" style="zoom:33%;" />
此時,將以S為根的子樹進行右旋轉
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹刪除情況4-2.png" alt="img" style="zoom:33%;" />
接著交換S和SL的顏色
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹刪除情況4-3.png" alt="img" style="zoom:33%;" />
節點SL的左孩子在旋轉前后不變,而SL原來為紅色,所以SL的左孩子必定為黑色。所以旋轉后對于N節點來說,相當于情況3。之后再通過情況3中的描述進行操作。整體上情況4需要進行一次右旋轉和一次左旋轉。
###### 5.N為黑色,S為紅色
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹刪除情況5-1.png" alt="img" style="zoom:33%;" />
此時,將以P為根的子樹進行左旋轉
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹刪除情況5-2.png" alt="img" style="zoom:33%;" />
將P和S顏色交換
<img src="https://hexo-rxy.oss-cn-beijing.aliyuncs.com/data_structure/RBTree/紅黑樹刪除情況5-3.png" alt="img" style="zoom:33%;" />
經過這樣的變換后,把該情形轉化成了N為黑色,其兄弟為黑色的情形,再通過以上描述的幾種情況進行變換,最終保持紅黑樹的性質。
#### 2.14.4 紅黑樹的性能
紅黑樹的增刪改查的復雜度顯然是O(logn)級別的,通常說紅黑樹是統計性能更優的樹結構。
為什么說統計性能更優呢?因為若是單純的讀操作,AVL樹的性能比紅黑樹強一些,紅黑樹不是嚴格的平衡樹,它是保持“黑平衡”的樹。對于紅黑樹,最壞的情況,是樹中最左側的節點的左子樹都是紅色的節點,即對應2-3樹中的“3節點”,所以這時紅黑樹的高度就是2logn(除了logn個黑色節點外,還有logn個紅色節點),紅黑樹要比AVL樹要高一些。所以從單純的查詢性能來說,紅黑樹的性能并沒有AVL樹強。
對于插入刪除操作來說,紅黑樹相比于AVL樹減少了左旋轉或右旋轉的次數,所以紅黑樹的插入刪除的性能比AVL樹強一些。
綜合增刪改查各方面的性能,紅黑樹的綜合性能比較高。
#### 2.14.5 紅黑樹的應用
1. Java中的TreeMap,Java8中HashMap的TreeNode節點采用了紅黑樹實現
2. C++中,STL的map和set也應用了紅黑樹
3. Linux中完全公平調度算法CFS(Completely Fair Schedule)
4. 用紅黑樹管理進程控制塊epoll在內核中的實現,用紅黑樹管理事件塊
5. Nginx中,用紅黑樹管理timer等