處理數字是 Common Lisp 的強項之一。Common Lisp 有著豐富的數值類型,而 Common Lisp 操作數字的特性與其他語言比起來更受人喜愛。
[TOC]
## 9.1 類型 (Types)[](http://acl.readthedocs.org/en/latest/zhCN/ch9-cn.html#types "Permalink to this headline")
Common Lisp 提供了四種不同類型的數字:整數、浮點數、比值與復數。本章所講述的函數適用于所有類型的數字。有幾個不能用在復數的函數會特別說明。
整數寫成一串數字:如?`2001`?。浮點數是可以寫成一串包含小數點的數字,如?`253.72`?,或是用科學表示法,如?`2.5372e2`?。比值是寫成由整數組成的分數:如?`2/3`?。而復數?`a+bi`?寫成?`#c(a?b)`?,其中?`a`?與?`b`?是任兩個類型相同的實數。
謂詞?`integerp`?、?`floatp`?以及?`complexp`?針對相應的數字類型返回真。圖 9.1 展示了數值類型的層級。
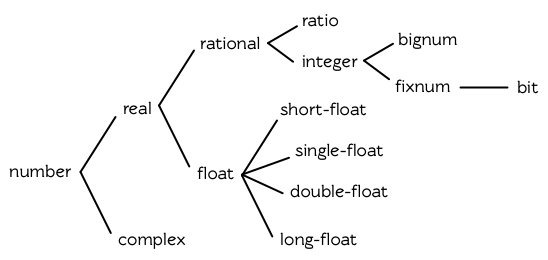
**圖 9.1: 數值類型**
要決定計算過程會返回何種數字,以下是某些通用的經驗法則:
1. 如果數值函數接受一個或多個浮點數作為參數,則返回值會是浮點數 (或是由浮點數組成的復數)。所以?`(+?1.0?2)`?求值為?`3.0`,而?`(+?#c(0?1.0)?2)`?求值為?`#c(2.0?1.0)`?。
2. 可約分的比值會被轉換成最簡分數。所以?`(/?10?2)`?會返回?`5`?。
3. 若計算過程中復數的虛部變成?`0`?時,則復數會被轉成實數 。所以?`(+?#c(1?-1)?#c(2?1))`?求值成?`3`?。
第二、第三個規則可以在讀入參數時直接應用,所以:
~~~
> (list (ratiop 2/2) (complexp #c(1 0)))
(NIL NIL)
~~~
## 9.2 轉換及取出 (Conversion and Extraction)[](http://acl.readthedocs.org/en/latest/zhCN/ch9-cn.html#conversion-and-extraction "Permalink to this headline")
Lisp 提供四種不同類型的數字的轉換及取出位數的函數。函數?`float`?將任何實數轉換成浮點數:
~~~
> (mapcar #'float '(1 2/3 .5))
(1.0 0.6666667 0.5)
~~~
將數字轉成整數未必需要轉換,因為它可能牽涉到某些資訊的喪失。函數?`truncate`?返回任何實數的整數部分:
~~~
> (truncate 1.3)
1
0.29999995
~~~
第二個返回值?`0.29999995`?是傳入的參數減去第一個返回值。(會有 0.00000005 的誤差是因為浮點數的計算本身就不精確。)
函數?`floor`?與?`ceiling`?以及?`round`?也從它們的參數中導出整數。使用?`floor`?返回小于等于其參數的最大整數,而?`ceiling`?返回大于或等于其參數的最小整數,我們可以將?`mirror?`?(46 頁,譯注: 3.11 節)改成可以找出所有回文(palindromes)的版本:
~~~
(defun palindrome? (x)
(let ((mid (/ (length x) 2)))
(equal (subseq x 0 (floor mid))
(reverse (subseq x (ceiling mid))))))
~~~
和?`truncate`?一樣,?`floor`?與?`ceiling`?也返回傳入參數與第一個返回值的差,作為第二個返回值。
~~~
> (floor 1.5)
1
0.5
~~~
實際上,我們可以把?`truncate`?想成是這樣定義的:
~~~
(defun our-truncate (n)
(if (> n 0)
(floor n)
(ceiling n)))
~~~
函數?`round`?返回最接近其參數的整數。當參數與兩個整數的距離相等時, Common Lisp 和很多程序語言一樣,不會往上取(round up)整數。而是取最近的偶數:
~~~
> (mapcar #'round '(-2.5 -1.5 1.5 2.5))
(-2 -2 2 2)
~~~
在某些數值應用中這是好事,因為舍入誤差(rounding error)通常會互相抵消。但要是用戶期望你的程序將某些值取整數時,你必須自己提供這個功能。?[[1]](http://acl.readthedocs.org/en/latest/zhCN/ch9-cn.html#id5)?與其他的函數一樣,?`round`?返回傳入參數與第一個返回值的差,作為第二個返回值。
函數?`mod`?僅返回?`floor`?返回的第二個返回值;而?`rem`?返回?`truncate`?返回的第二個返回值。我們在 94 頁(譯注: 5.7 節)曾使用`mod`?來決定一個數是否可被另一個整除,以及 127 頁(譯注: 7.4 節)用來找出環狀緩沖區(ring buffer)中,元素實際的位置。
關于實數,函數?`signum`?返回?`1`?、?`0`?或?`-1`?,取決于它的參數是正數、零或負數。函數?`abs`?返回其參數的絕對值。因此?`(*?(absx)?(signum?x))`?等于?`x`?。
~~~
> (mapcar #'signum '(-2 -0.0 0.0 0 .5 3))
(-1 -0.0 0.0 0 1.0 1)
~~~
在某些應用里,?`-0.0`?可能自成一格(in its own right),如上所示。實際上功能上幾乎沒有差別,因為數值?`-0.0`?與?`0.0`?有著一樣的行為。
比值與復數概念上是兩部分的結構。(譯注:像?**Cons**?這樣的兩部分結構) 函數?`numerator`?與?`denominator`?返回比值或整數的分子與分母。(如果數字是整數,前者返回該數,而后者返回?`1`?。)函數?`realpart`?與?`imgpart`?返回任何數字的實數與虛數部分。(如果數字不是復數,前者返回該數字,后者返回?`0`?。)
函數?`random`?接受一個整數或浮點數。這樣形式的表達式?`(random?n)`?,會返回一個大于等于?`0`?并小于?`n`?的數字,并有著與?`n`?相同的類型。
## 9.3 比較 (Comparison)[](http://acl.readthedocs.org/en/latest/zhCN/ch9-cn.html#comparison "Permalink to this headline")
謂詞?`=`?比較其參數,當數值上相等時 ── 即兩者的差為零時,返回真。
~~~
> (= 1 1.0)
T
> (eql 1 1.0)
NIL
~~~
`=`?比起?`eql`?來得寬松,但參數的類型需一致。
用來比較數字的謂詞為?`<`?(小于)、?`<=`?(小于等于)、?`=`?(等于)、?`>=`?(大于等于)、?`>`?(大于) 以及?`/=`?(不相等)。以上所有皆接受一個或多個參數。只有一個參數時,它們全返回真。
~~~
(<= w x y z)
~~~
等同于二元操作符的結合(conjunction),應用至每一對參數上:
~~~
(and (<= w x) (<= x y) (<= y z))
~~~
由于?`/=`?若它的兩個參數不等于時會返回真,表達式
~~~
(/= w x y z)
~~~
等同于
~~~
(and (/= w x) (/= w y) (/= w z)
(/= x y) (/= y z) (/= y z))
~~~
特殊的謂詞?`zerop`?、?`plusp`?與?`minusp`?接受一個參數,分別于參數?`=`?、?`>`?、?`<`?零時,返回真。雖然?`-0.0`?(如果實現有使用它)前面有個負號,但它?`=`?零,
~~~
> (list (minusp -0.0) (zerop -0.0))
(NIL T)
~~~
因此對?`-0.0`?使用?`zerop`?,而不是?`minusp`?。
謂詞?`oddp`?與?`evenp`?只能用在整數。前者只對奇數返回真,后者只對偶數返回真。
本節定義的謂詞中,只有?`=`?、?`/=`?與?`zerop`?可以用在復數。
函數?`max`?與?`min`?分別返回其參數的最大值與最小值。兩者至少需要給一個參數:
~~~
> (list (max 1 2 3 4 5) (min 1 2 3 4 5))
(5 1)
~~~
如果參數含有浮點數的話,結果的類型取決于各家實現。
## 9.4 算術 (Arithematic)[](http://acl.readthedocs.org/en/latest/zhCN/ch9-cn.html#arithematic "Permalink to this headline")
用來做加減的函數是?`+`?與?`-`?。兩者皆接受任何數量的參數,包括沒有參數,在沒有參數的情況下返回?`0`?。(譯注:?`-`?在沒有參數的情況下會報錯,至少要一個參數)一個這樣形式的表達式?`(-?n)`?返回?`-n`?。一個這樣形式的表達式
~~~
(- x y z)
~~~
等同于
~~~
(- (- x y) z)
~~~
有兩個函數?`1+`?與?`1-`?,分別將參數加?`1`?與減?`1`?后返回。?`1-`?有一點誤導,因為?`(1-?x)`?返回?`x-1`?而不是?`1-x`?。
宏?`incf`?及?`decf`?分別遞增與遞減數字。這樣形式的表達式?`(incf?x?n)`?類似于?`(setf?x?(+?x?n))`?的效果,而?`(decf?x?n)`?類似于?`(setf?x?(-?x?n))`?的效果。這兩個形式里,第二個參數皆是選擇性給入的,缺省值為?`1`?。
用來做乘法的函數是?`*`?。接受任何數量的參數。沒有參數時返回?`1`?。否則返回參數的乘積。
除法函數?`/`?至少要給一個參數。這樣形式的調用?`(/?n)`?等同于?`(/?1?n)`?,
~~~
> (/ 3)
1/3
~~~
而這樣形式的調用
~~~
(/ x y z)
~~~
等同于
~~~
(/ (/ x y) z)
~~~
注意?`-`?與?`/`?兩者在這方面的相似性。
當給定兩個整數時,?`/`?若第一個不是第二個的倍數時,會返回一個比值:
~~~
> (/ 365 12)
365/12
~~~
舉例來說,如果你試著找出平均每一個月有多長,可能會有解釋器在逗你玩的感覺。在這個情況下,你需要的是,對比值調用?`float`,而不是對兩個整數做?`/`?。
~~~
> (float 365/12)
30.416666
~~~
## 9.5 指數 (Exponentiation)[](http://acl.readthedocs.org/en/latest/zhCN/ch9-cn.html#exponentiation "Permalink to this headline")
要找到?xn?調用?`(expt?x?n)`?,
~~~
> (expt 2 5)
32
~~~
而要找到?lognx?調用?`(log?x?n)`?:
~~~
> (log 32 2)
5.0
~~~
通常返回一個浮點數。
要找到?ex?有一個特別的函數?`exp`?,
~~~
> (exp 2)
7.389056
~~~
而要找到自然對數,你可以使用?`log`?就好,因為第二個參數缺省為?`e`?:
~~~
> (log 7.389056)
2.0
~~~
要找到立方根,你可以調用?`expt`?用一個比值作為第二個參數,
~~~
> (expt 27 1/3)
3.0
~~~
但要找到平方根,函數?`sqrt`?會比較快:
~~~
> (sqrt 4)
2.0
~~~
## 9.6 三角函數 (Trigometric Functions)[](http://acl.readthedocs.org/en/latest/zhCN/ch9-cn.html#trigometric-functions "Permalink to this headline")
常量?`pi`?是?`π`?的浮點表示法。它的精度取決于各家實現。函數?`sin`?、?`cos`?及?`tan`?分別可以找到正弦、余弦及正交函數,其中角度以徑度表示:
~~~
> (let ((x (/ pi 4)))
(list (sin x) (cos x) (tan x)))
(0.7071067811865475d0 0.7071067811865476d0 1.0d0)
;;; 譯注: CCL 1.8 SBCL 1.0.55 下的結果是
;;; (0.7071067811865475D0 0.7071067811865476D0 0.9999999999999999D0)
~~~
這些函數都接受負數及復數參數。
函數?`asin`?、?`acos`?及?`atan`?實現了正弦、余弦及正交的反函數。參數介于?`-1`?與?`1`?之間(包含)時,?`asin`?與?`acos`?返回實數。
雙曲正弦、雙曲余弦及雙曲正交分別由?`sinh`?、?`cosh`?及?`tanh`?實現。它們的反函數同樣為?`asinh`?、?`acosh`?以及?`atanh`?。
## 9.7 表示法 (Representations)[](http://acl.readthedocs.org/en/latest/zhCN/ch9-cn.html#representations "Permalink to this headline")
Common Lisp 沒有限制整數的大小。可以塞進一個字(word)內存的小整數稱為定長數(fixnums)。在計算過程中,整數無法塞入一個字時,Lisp 切換至使用多個字的表示法(一個大數 「bignum」)。所以整數的大小限制取決于實體內存,而不是語言。
常量?`most-positive-fixnum`?與?`most-negative-fixnum`?表示一個實現不使用大數所可表示的最大與最小的數字大小。在很多實現里,它們為:
~~~
> (values most-positive-fixnum most-negative-fixnum)
536870911
-536870912
;;; 譯注: CCL 1.8 的結果為
1152921504606846975
-1152921504606846976
;;; SBCL 1.0.55 的結果為
4611686018427387903
-4611686018427387904
~~~
謂詞?`typep`?接受一個參數及一個類型名稱,并返回指定類型的參數。所以,
~~~
> (typep 1 'fixnum)
T
> (type (1+ most-positive-fixnum) 'bignum)
T
~~~
浮點數的數值限制是取決于各家實現的。 Common Lisp 提供了至多四種類型的浮點數:短浮點?`short-float`?、 單浮點?`single-float`?、雙浮點?`double-float`?以及長浮點?`long-float`?。Common Lisp 的實現是不需要用不同的格式來表示這四種類型(很少有實現這么干)。
一般來說,短浮點應可塞入一個字,單浮點與雙浮點提供普遍的單精度與雙精度浮點數的概念,而長浮點,如果想要的話,可以是很大的數。但實現可以不對這四種類型做區別,也是完全沒有問題的。
你可以指定你想要何種格式的浮點數,當數字是用科學表示法時,可以通過將?`e`?替換為?`s`?`f`?`d`?`l`?來得到不同的浮點數。(你也可以使用大寫,這對長浮點來說是個好主意,因為?`l`?看起來太像?`1`?了。)所以要表示最大的?`1.0`?你可以寫?`1L0`?。
(譯注:?`s`?為短浮點、?`f`?為單浮點、?`d`?為雙浮點、?`l`?為長浮點。)
在給定的實現里,用十六個全局常量標明了每個格式的限制。它們的名字是這種形式:?`m-s-f`?,其中?`m`?是?`most`?或?`least`?,?`s`?是`positive`?或?`negative`?,而?`f`?是四種浮點數之一。?[λ](http://acl.readthedocs.org/en/latest/zhCN/notes-cn.html#notes-150)
浮點數下溢(underflow)與溢出(overflow),都會被 Common Lisp 視為錯誤 :
~~~
> (* most-positive-long-float 10)
Error: floating-point-overflow
~~~
## 9.8 范例:追蹤光線 (Example: Ray-Tracing)[](http://acl.readthedocs.org/en/latest/zhCN/ch9-cn.html#example-ray-tracing "Permalink to this headline")
作為一個數值應用的范例,本節示范了如何撰寫一個光線追蹤器 (ray-tracer)。光線追蹤是一個高級的 (deluxe)渲染算法: 它產生出逼真的圖像,但需要花點時間。
要產生一個 3D 的圖像,我們至少需要定義四件事: 一個觀測點 (eye)、一個或多個光源、一個由一個或多個平面所組成的模擬世界 (simulated world),以及一個作為通往這個世界的窗戶的平面 (圖像平面「image plane」)。我們產生出的是模擬世界投影在圖像平面區域的圖像。
光線追蹤獨特的地方在于,我們如何找到這個投影: 我們一個一個像素地沿著圖像平面走,追蹤回到模擬世界里的光線。這個方法帶來三個主要的優勢: 它讓我們容易得到現實世界的光學效應 (optical effect),如透明度 (transparency)、反射光 (reflected light)以及產生陰影 (cast shadows);它讓我們可以直接用任何我們想要的幾何的物體,來定義出模擬的世界,而不需要用多邊形 (polygons)來建構它們;以及它很簡單實現。
~~~
(defun sq (x) (* x x))
(defun mag (x y z)
(sqrt (+ (sq x) (sq y) (sq z))))
(defun unit-vector (x y z)
(let ((d (mag x y z)))
(values (/ x d) (/ y d) (/ z d))))
(defstruct (point (:conc-name nil))
x y z)
(defun distance (p1 p2)
(mag (- (x p1) (x p2))
(- (y p1) (y p2))
(- (z p1) (z p2))))
(defun minroot (a b c)
(if (zerop a)
(/ (- c) b)
(let ((disc (- (sq b) (* 4 a c))))
(unless (minusp disc)
(let ((discrt (sqrt disc)))
(min (/ (+ (- b) discrt) (* 2 a))
(/ (- (- b) discrt) (* 2 a))))))))
~~~
**圖 9.2 實用數學函數**
圖 9.2 包含了我們在光線追蹤器里會需要用到的一些實用數學函數。第一個?`sq`?,返回其參數的平方。下一個?`mag`?,返回一個給定?`x``y`?`z`?所組成向量的大小 (magnitude)。這個函數被接下來兩個函數用到。我們在?`unit-vector`?用到了,此函數返回三個數值,來表示與單位向量有著同樣方向的向量,其中向量是由?`x`?`y`?`z`?所組成的:
~~~
> (multiple-value-call #'mag (unit-vector 23 12 47))
1.0
~~~
我們在?`distance`?也用到了?`mag`?,它返回三維空間中,兩點的距離。(定義?`point`?結構來有一個?`nil`?的?`conc-name`?意味著欄位存取的函數會有跟欄位一樣的名字: 舉例來說,?`x`?而不是?`point-x`?。)
最后?`minroot`?接受三個實數,?`a`?,?`b`?與?`c`?,并返回滿足等式?ax2+bx+c=0?的最小實數?`x`?。當?`a`?不為?0?時,這個等式的根由下面這個熟悉的式子給出:
x=?b±b2?4ac???????√2a
圖 9.3 包含了定義一個最小光線追蹤器的代碼。 它產生通過單一光源照射的黑白圖像,與觀測點 (eye)處于同個位置。 (結果看起來像是閃光攝影術 (flash photography)拍出來的)
`surface`?結構用來表示模擬世界中的物體。更精確的說,它會被?`included`?至定義具體類型物體的結構里,像是球體 (spheres)。`surface`?結構本身只包含一個欄位: 一個?`color`?范圍從 0 (黑色) 至 1 (白色)。
~~~
(defstruct surface color)
(defparameter *world* nil)
(defconstant eye (make-point :x 0 :y 0 :z 200))
(defun tracer (pathname &optional (res 1))
(with-open-file (p pathname :direction :output)
(format p "P2 ~A ~A 255" (* res 100) (* res 100))
(let ((inc (/ res)))
(do ((y -50 (+ y inc)))
((< (- 50 y) inc))
(do ((x -50 (+ x inc)))
((< (- 50 x) inc))
(print (color-at x y) p))))))
(defun color-at (x y)
(multiple-value-bind (xr yr zr)
(unit-vector (- x (x eye))
(- y (y eye))
(- 0 (z eye)))
(round (* (sendray eye xr yr zr) 255))))
(defun sendray (pt xr yr zr)
(multiple-value-bind (s int) (first-hit pt xr yr zr)
(if s
(* (lambert s int xr yr zr) (surface-color s))
0)))
(defun first-hit (pt xr yr zr)
(let (surface hit dist)
(dolist (s *world*)
(let ((h (intersect s pt xr yr zr)))
(when h
(let ((d (distance h pt)))
(when (or (null dist) (< d dist))
(setf surface s hit h dist d))))))
(values surface hit)))
(defun lambert (s int xr yr zr)
(multiple-value-bind (xn yn zn) (normal s int)
(max 0 (+ (* xr xn) (* yr yn) (* zr zn)))))
~~~
**圖 9.3 光線追蹤。**
圖像平面會是由 x 軸與 y 軸所定義的平面。觀測者 (eye) 會在 z 軸,距離原點 200 個單位。所以要在圖像平面可以被看到,插入至`*worlds*`?的表面 (一開始為?`nil`)會有著負的 z 座標。圖 9.4 說明了一個光線穿過圖像平面上的一點,并擊中一個球體。
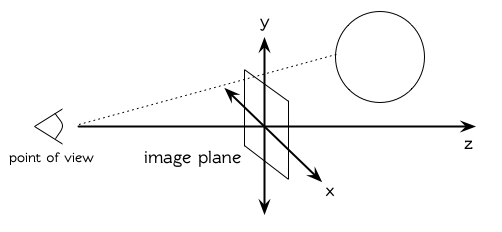
**圖 9.4: 追蹤光線。**
函數?`tracer`?接受一個路徑名稱,并寫入一張圖片至對應的文件。圖片文件會用一種簡單的 ASCII 稱作 PGM 的格式寫入。默認情況下,圖像會是 100x100 。我們 PGM 文件的標頭 (headers) 會由標簽?`P2`?組成,伴隨著指定圖片寬度 (breadth)與高度 (height)的整數,初始為 100,單位為 pixel,以及可能的最大值 (255)。文件剩余的部份會由 10000 個介于 0 (黑)與 1 (白)整數組成,代表著 100 條 100 像素的水平線。
圖片的解析度可以通過給入明確的?`res`?來調整。舉例來說,如果?`res`?是?`2`?,則同樣的圖像會被渲染成 200x200 。
圖片是一個在圖像平面 100x100 的正方形。每一個像素代表著穿過圖像平面抵達觀測點的光的數量。要找到每個像素光的數量,`tracer`?調用?`color-at`?。這個函數找到從觀測點至該點的向量,并調用?`sendray`?來追蹤這個向量回到模擬世界的軌跡;?`sandray`?會返回一個數值介于 0 與 1 之間的亮度 (intensity),之后會縮放成一個 0 至 255 的整數來顯示。
要決定一個光線的亮度,?`sendray`?需要找到光是從哪個物體所反射的。要辦到這件事,我們調用?`first-hit`?,此函數研究在`*world*`?里的所有平面,并返回光線最先抵達的平面(如果有的話)。如果光沒有擊中任何東西,?`sendray`?僅返回背景顏色,按慣例是?`0`?(黑色)。如果光線有擊中某物的話,我們需要找出在光擊中時,有多少數量的光照在該平面。
[朗伯定律](http://zh.wikipedia.org/zh-tw/%E6%AF%94%E5%B0%94%EF%BC%8D%E6%9C%97%E4%BC%AF%E5%AE%9A%E5%BE%8B)?告訴我們,由平面上一點所反射的光的強度,正比于該點的單位法向量 (unit normal vector)?*N*?(這里是與平面垂直且長度為一的向量)與該點至光源的單位向量?*L*?的點積 (dot-product):
i=N?L
如果光剛好照到這點,?*N*?與?*L*?會重合 (coincident),則點積會是最大值,?`1`?。如果將在這時候將平面朝光轉 90 度,則?*N*?與?*L*?會垂直,則兩者點積會是?`0`?。如果光在平面后面,則點積會是負數。
在我們的程序里,我們假設光源在觀測點 (eye),所以?`lambert`?使用了這個規則來找到平面上某點的亮度 (illumination),返回我們追蹤的光的單位向量與法向量的點積。
在?`sendray`?這個值會乘上平面的顏色 (即便是有好的照明,一個暗的平面還是暗的)來決定該點之后總體亮度。
為了簡單起見,我們在模擬世界里會只有一種物體,球體。圖 9.5 包含了與球體有關的代碼。球體結構包含了?`surface`?,所以一個球體會有一種顏色以及?`center`?和?`radius`?。調用?`defsphere`?添加一個新球體至世界里。
~~~
(defstruct (sphere (:include surface))
radius center)
(defun defsphere (x y z r c)
(let ((s (make-sphere
:radius r
:center (make-point :x x :y y :z z)
:color c)))
(push s *world*)
s))
(defun intersect (s pt xr yr zr)
(funcall (typecase s (sphere #'sphere-intersect))
s pt xr yr zr))
(defun sphere-intersect (s pt xr yr zr)
(let* ((c (sphere-center s))
(n (minroot (+ (sq xr) (sq yr) (sq zr))
(* 2 (+ (* (- (x pt) (x c)) xr)
(* (- (y pt) (y c)) yr)
(* (- (z pt) (z c)) zr)))
(+ (sq (- (x pt) (x c)))
(sq (- (y pt) (y c)))
(sq (- (z pt) (z c)))
(- (sq (sphere-radius s)))))))
(if n
(make-point :x (+ (x pt) (* n xr))
:y (+ (y pt) (* n yr))
:z (+ (z pt) (* n zr))))))
(defun normal (s pt)
(funcall (typecase s (sphere #'sphere-normal))
s pt))
(defun sphere-normal (s pt)
(let ((c (sphere-center s)))
(unit-vector (- (x c) (x pt))
(- (y c) (y pt))
(- (z c) (z pt)))))
~~~
**圖 9.5 球體。**
函數?`intersect`?判斷與何種平面有關,并調用對應的函數。在此時只有一種,?`sphere-intersect`?,但?`intersect`?是寫成可以容易擴展處理別種物體。
我們要怎么找到一束光與一個球體的交點 (intersection)呢?光線是表示成點?p=?x0,y0,x0??以及單位向量?v=?xr,yr,xr??。每個在光上的點可以表示為?p+nv?,對于某個?*n*?── 即??x0+nxr,y0+nyr,z0+nzr??。光擊中球體的點的距離至中心??xc,yc,zc??會等于球體的半徑?*r*?。所以在下列這個交點的方程序會成立:
r=(x0+nxr?xc)2+(y0+nyr?yc)2+(z0+nzr?zc)2??????????????????????????????????????????√
這會給出
an2+bn+c=0
其中
a=x2r+y2r+z2rb=2((x0?xc)xr+(y0?yc)yr+(z0?zc)zr)c=(x0?xc)2+(y0?yc)2+(z0?zc)2?r2
要找到交點我們只需要找到這個二次方程序的根。它可能是零、一個或兩個實數根。沒有根代表光沒有擊中球體;一個根代表光與球體交于一點 (擦過 「grazing hit」);兩個根代表光與球體交于兩點 (一點交于進入時、一點交于離開時)。在最后一個情況里,我們想要兩個根之中較小的那個;?*n*?與光離開觀測點的距離成正比,所以先擊中的會是較小的?*n*?。所以我們調用?`minroot`?。如果有一個根,?`sphere-intersect`?返回代表該點的??x0+nxr,y0+nyr,z0+nzr??。
圖 9.5 的另外兩個函數,?`normal`?與?`sphere-normal`?類比于?`intersect`?與?`sphere-intersect`?。要找到垂直于球體很簡單 ── 不過是從該點至球體中心的向量而已。
圖 9.6 示范了我們如何產生圖片;?`ray-test`?定義了 38 個球體(不全都看的見)然后產生一張圖片,叫做 “sphere.pgm” 。
(譯注:PGM 可移植灰度圖格式,更多信息參見?[wiki](http://en.wikipedia.org/wiki/Portable_graymap)?)
~~~
(defun ray-test (&optional (res 1))
(setf *world* nil)
(defsphere 0 -300 -1200 200 .8)
(defsphere -80 -150 -1200 200 .7)
(defsphere 70 -100 -1200 200 .9)
(do ((x -2 (1+ x)))
((> x 2))
(do ((z 2 (1+ z)))
((> z 7))
(defsphere (* x 200) 300 (* z -400) 40 .75)))
(tracer (make-pathname :name "spheres.pgm") res))
~~~
**圖 9.6 使用光線追蹤器**
圖 9.7 是產生出來的圖片,其中?`res`?參數為 10。

**圖 9.7: 追蹤光線的圖**
一個實際的光線追蹤器可以產生更復雜的圖片,因為它會考慮更多,我們只考慮了單一光源至平面某一點。可能會有多個光源,每一個有不同的強度。它們通常不會在觀測點,在這個情況程序需要檢查至光源的向量是否與其他平面相交,這會在第一個相交的平面上產生陰影。將光源放置于觀測點讓我們不需要考慮這麼復雜的情況,因為我們看不見在陰影中的任何點。
一個實際的光線追蹤器不僅追蹤光第一個擊中的平面,也會加入其它平面的反射光。一個實際的光線追蹤器會是有顏色的,并可以模型化出透明或是閃耀的平面。但基本的算法會與圖 9.3 所演示的差不多,而許多改進只需要遞回的使用同樣的成分。
一個實際的光線追蹤器可以是高度優化的。這里給出的程序為了精簡寫成,甚至沒有如 Lisp 程序員會最佳化的那樣,就僅是一個光線追蹤器而已。僅加入類型與行內宣告 (13.3 節)就可以讓它變得兩倍以上快。
## Chapter 9 總結 (Summary)[](http://acl.readthedocs.org/en/latest/zhCN/ch9-cn.html#chapter-9-summary "Permalink to this headline")
1. Common Lisp 提供整數 (integers)、比值 (ratios)、浮點數 (floating-point numbers)以及復數 (complex numbers)。
2. 數字可以被約分或轉換 (converted),而它們的位數 (components)可以被取出。
3. 用來比較數字的謂詞可以接受任意數量的參數,以及比較下一數對 (successive pairs) ──?/=?函數除外,它是用來比較所有的數對 (pairs)。
4. Common Lisp 幾乎提供你在低階科學計算機可以看到的數值函數。同樣的函數普遍可應用在多種類型的數字上。
5. Fixnum 是小至可以塞入一個字 (word)的整數。它們在必要時會悄悄但花費昂貴地轉成大數 (bignum)。Common Lisp 提供最多四種浮點數。每一個浮點表示法的限制是實現相關的 (implementation-dependent)常量。
6. 一個光線追蹤器 (ray-tracer)通過追蹤光線來產生圖像,使得每一像素回到模擬的世界。
## Chapter 9 練習 (Exercises)[](http://acl.readthedocs.org/en/latest/zhCN/ch9-cn.html#chapter-9-exercises "Permalink to this headline")
1. 定義一個函數,接受一個實數列表,若且唯若 (iff)它們是非遞減 (nondecreasing)順序時返回真。
2. 定義一個函數,接受一個整數?`cents`?并返回四個值,將數字用?`25-`?,?`10-`?,?`5-`?,?`1-`?來顯示,使用最少數量的硬幣。(譯注:?`25-`?是 25 美分,以此類推)
3. 一個遙遠的星球住著兩種生物, wigglies 與 wobblies 。 Wigglies 與 wobblies 唱歌一樣厲害。每年都有一個比賽來選出十大最佳歌手。下面是過去十年的結果:
| YEAR | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| WIGGLIES | 6 | 5 | 6 | 4 | 5 | 5 | 4 | 5 | 6 | 5 |
| WOBBLIES | 4 | 5 | 4 | 6 | 5 | 5 | 6 | 5 | 4 | 5 |
寫一個程序來模擬這樣的比賽。你的結果實際上有建議委員會每年選出 10 個最佳歌手嗎?
1. 定義一個函數,接受 8 個表示二維空間中兩個線段端點的實數,若線段沒有相交,則返回假,或返回兩個值表示相交點的?`x`?座標與?`y`?座標。
2. 假設?`f`?是一個接受一個 (實數) 參數的函數,而?`min`?與?`max`?是有著不同正負號的非零實數,使得?`f`?對于參數?`i`?有一個根 (返回零)并滿足?`min?<?i?<?max`?。定義一個函數,接受四個參數,?`f`?,?`min`?,?`max`?以及?`epsilon`?,并返回一個?`i`?的近似值,準確至正負?`epsilon`?之內。
3. *Honer’s method*?是一個有效率求出多項式的技巧。要找到?ax3+bx2+cx+d?你對?`x(x(ax+b)+c)+d`?求值。定義一個函數,接受一個或多個參數 ── x 的值伴隨著?*n*?個實數,用來表示?`(n-1)`?次方的多項式的系數 ── 并用?*Honer’s method*?計算出多項式的值。
譯注:?[Honer’s method on wiki](http://en.wikipedia.org/wiki/Horner's_method)
1. 你的 Common Lisp 實現使用了幾個位元來表示定長數?
2. 你的 Common Lisp 實現提供幾種不同的浮點數?
腳注
[[1]](http://acl.readthedocs.org/en/latest/zhCN/ch9-cn.html#id2) | 當?`format`?取整顯示時,它不保證會取成偶數或奇數。見 125 頁 (譯注: 7.4 節)。
