3.3 節中介紹了 Lisp 如何使用指針允許我們將任何值放到任何地方。這種說法是完全有可能的,但這并不一定都是好事。
例如,一個對象可以是它自已的一個元素。這是好事還是壞事,取決于程序員是不是有意這樣設計的。
[TOC]
## 12.1 共享結構 (Shared Structure)[](http://acl.readthedocs.org/en/latest/zhCN/ch12-cn.html#shared-structure "Permalink to this headline")
多個列表可以共享?`cons`?。在最簡單的情況下,一個列表可以是另一個列表的一部分。
~~~
> (setf part (list 'b 'c))
(B C)
> (setf whole (cons 'a part))
(A B C)
~~~
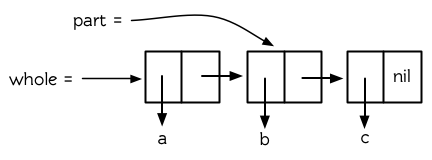
**圖 12.1 共享結構**
執行上述操作后,第一個?`cons`?是第二個?`cons`?的一部分 (事實上,是第二個?`cons`?的?`cdr`?)。在這樣的情況下,我們說,這兩個列表是共享結構 (Share Structure)。這兩個列表的基本結構如圖 12.1 所示。
其中,第一個?`cons`?是第二個?`cons`?的一部分 (事實上,是第二個?`cons`?的?`cdr`?)。在這樣的情況下,我們稱這兩個列表為共享結構 (Share Structure)。這兩個列表的基本結構如圖 12.1 所示。
使用?`tailp`?判斷式來檢測一下。將兩個列表作為它的輸入參數,如果第一個列表是第二個列表的一部分時,則返回?`T`?:
~~~
> (tailp part whole)
T
~~~
我們可以把它想像成:
~~~
(defun our-tailp (x y)
(or (eql x y)
(and (consp y)
(our-tailp x (cdr y)))))
~~~
如定義所表明的,每個列表都是它自己的尾端,?`nil`?是每一個正規列表的尾端。
在更復雜的情況下,兩個列表可以是共享結構,但彼此都不是對方的尾端。在這種情況下,他們都有一個共同的尾端,如圖 12.2 所示。我們像這樣構建這種情況:
~~~
(setf part (list 'b 'c)
whole1 (cons 1 part)
whole2 (cons 2 part))
~~~
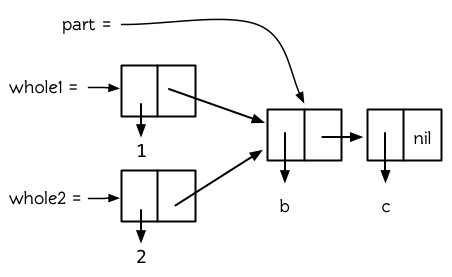
**圖 12.2 被共享的尾端**
現在?`whole1`?和?`whole2`?共享結構,但是它們彼此都不是對方的一部分。
當存在嵌套列表時,重要的是要區分是列表共享了結構,還是列表的元素共享了結構。頂層列表結構指的是,直接構成列表的那些`cons`?,而不包含那些用于構造列表元素的?`cons`?。圖 12.3 是一個嵌套列表的頂層列表結構 (**譯者注:**圖 12.3 中上面那三個有黑色陰影的?`cons`?即構成頂層列表結構的?`cons`?)。
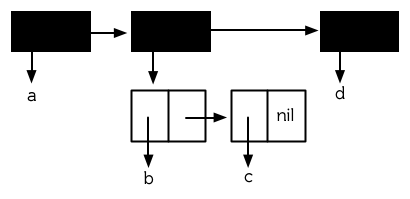
**圖 12.3 頂層列表結構**
兩個?`cons`?是否共享結構,取決于我們把它們看作是列表還是[樹](http://zh.wikipedia.org/wiki/%E6%A0%91_(%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84))。可能存在兩個嵌套列表,當把它們看作樹時,它們共享結構,而看作列表時,它們不共享結構。圖 12.4 構建了這種情況,兩個列表以一個元素的形式包含了同一個列表,代碼如下:
~~~
(setf element (list 'a 'b)
holds1 (list 1 element 2)
holds2 (list element 3))
~~~
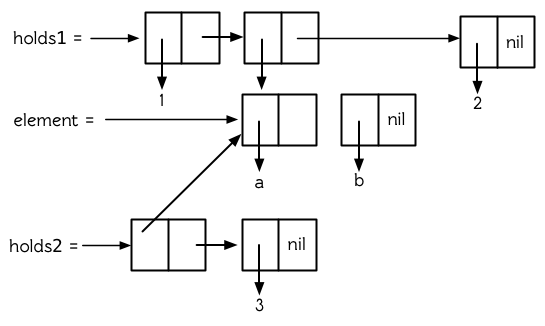
**圖 12.4 共享子樹**
雖然?`holds1`?的第二個元素和?`holds2`?的第一個元素共享結構 (其實是相同的),但如果把?`holds1`?和?`holds2`?看成是列表時,它們不共享結構。僅當兩個列表共享頂層列表結構時,才能說這兩個列表共享結構,而?`holds1`?和?`holds2`?沒有共享頂層列表結構。
如果我們想避免共享結構,可以使用復制。函數?`copy-list`?可以這樣定義:
~~~
(defun our-copy-list (lst)
(if (null lst)
nil
(cons (car lst) (our-copy-list (cdr lst)))))
~~~
它返回一個不與原始列表共享頂層列表結構的新列表。函數?`copy-tree`?可以這樣定義:
~~~
(defun our-copy-tree (tr)
(if (atom tr)
tr
(cons (our-copy-tree (car tr))
(our-copy-tree (cdr tr)))))
~~~
它返回一個連原始列表的樹型結構也不共享的新列表。圖 12.5 顯示了對一個嵌套列表使用?`copy-list`?和?`copy-tree`?的區別。
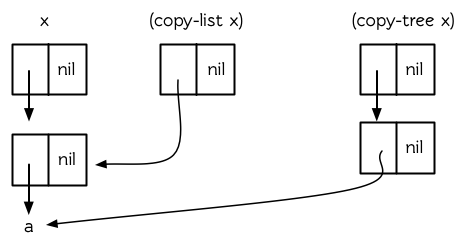
**圖 12.5 兩種復制**
## 12.2 修改 (Modification)[](http://acl.readthedocs.org/en/latest/zhCN/ch12-cn.html#modification "Permalink to this headline")
為什么要避免共享結構呢?之前討論的共享結構問題僅僅是個智力練習,到目前為止,并沒使我們在實際寫程序的時候有什么不同。當修改一個被共享的結構時,問題出現了。如果兩個列表共享結構,當我們修改了其中一個,另外一個也會無意中被修改。
上一節中,我們介紹了怎樣構建一個是其它列表的尾端的列表:
~~~
(setf whole (list 'a 'b 'c)
tail (cdr whole))
~~~
因為?`whole`?的?`cdr`?與?`tail`?是相等的,無論是修改?`tail`?還是?`whole`?的?`cdr`?,我們修改的都是同一個?`cons`?:
~~~
> (setf (second tail ) 'e)
E
> tail
(B E)
> whole
(A B E)
~~~
同樣的,如果兩個列表共享同一個尾端,這種情況也會發生。
一次修改兩個對象并不總是錯誤的。有時候這可能正是你想要的。但如果無意的修改了共享結構,將會引入一些非常微妙的 bug。Lisp 程序員要培養對共享結構的意識,并且在這類錯誤發生時能夠立刻反應過來。當一個列表神秘的改變了的時候,很有可能是因為改變了其它與之共享結構的對象。
真正危險的不是共享結構,而是改變被共享的結構。為了安全起見,干脆避免對結構使用?`setf`?(以及相關的運算,比如:?`pop`?,`rplaca`?等),這樣就不會遇到問題了。如果某些時候不得不修改列表結構時,要搞清楚要修改的列表的來源,確保它不要和其它不需要改變的對象共享結構。如果它和其它不需要改變的對象共享了結構,或者不能預測它的來源,那么復制一個副本來進行改變。
當你調用別人寫的函數的時候要加倍小心。除非你知道它內部的操作,否則,你傳入的參數時要考慮到以下的情況:
1.它對你傳入的參數可能會有破壞性的操作
2.你傳入的參數可能被保存起來,如果你調用了一個函數,然后又修改了之前作為參數傳入該函數的對象,那么你也就改變了函數已保存起來作為它用的對象[1]。
在這兩種情況下,解決的方法是傳入一個拷貝。
在 Common Lisp 中,一個函數調用在遍歷列表結構 (比如,?`mapcar`?或?`remove-if`?的參數)的過程中不允許修改被遍歷的結構。關于評估這樣的代碼的重要性并沒有明確的規定。
## 12.3 示例:隊列 (Example: Queues)[](http://acl.readthedocs.org/en/latest/zhCN/ch12-cn.html#example-queues "Permalink to this headline")
共享結構并不是一個總讓人擔心的特性。我們也可以對其加以利用的。這一節展示了怎樣用共享結構來表示[隊列](http://zh.wikipedia.org/wiki/%E9%98%9F%E5%88%97)。隊列對象是我們可以按照數據的插入順序逐個檢出數據的倉庫,這個規則叫做[先進先出 (FIFO, first in, first out)](http://zh.wikipedia.org/zh-cn/%E5%85%88%E9%80%B2%E5%85%88%E5%87%BA)。
用列表表示[棧 (stack)](http://zh.wikipedia.org/wiki/%E6%A0%88)比較容易,因為棧是從同一端插入和檢出。而表示隊列要困難些,因為隊列的插入和檢出是在不同端。為了有效的實現隊列,我們需要找到一種辦法來指向列表的兩個端。
圖 12.6 給出了一種可行的策略。它展示怎樣表示一個含有 a,b,c 三個元素的隊列。一個隊列就是一對列表,最后那個?`cons`?在相同的列表中。這個列表對由被稱作頭端 (front)和尾端 (back)的兩部分組成。如果要從隊列中檢出一個元素,只需在其頭端?`pop`,要插入一個元素,則創建一個新的?`cons`?,把尾端的?`cdr`?設置成指向這個?`cons`?,然后將尾端指向這個新的?`cons`?。
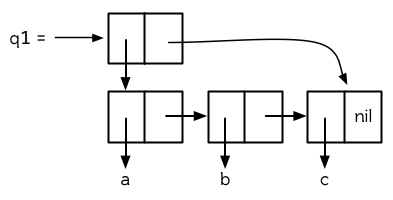
**圖 12.6 一個隊列的結構**
~~~
(defun make-queue () (cons nil nil))
(defun enqueue (obj q)
(if (null (car q))
(setf (cdr q) (setf (car q) (list obj)))
(setf (cdr (cdr q)) (list obj)
(cdr q) (cdr (cdr q))))
(car q))
(defun dequeue (q)
(pop (car q)))
~~~
**圖 12.7 隊列實現**
圖 12.7 中的代碼實現了這一策略。其用法如下:
~~~
> (setf q1 (make-queue))
(NIL)
> (progn (enqueue 'a q1)
(enqueue 'b q1)
(enqueue 'c q1))
(A B C)
~~~
現在,?`q1`?的結構就如圖 12.6 那樣:
~~~
> q1
((A B C) C)
~~~
從隊列中檢出一些元素:
~~~
> (dequeue q1)
A
> (dequeue q1)
B
> (enqueue 'd q1)
(C D)
~~~
## 12.4 破壞性函數 (Destructive Functions)[](http://acl.readthedocs.org/en/latest/zhCN/ch12-cn.html#destructive-functions "Permalink to this headline")
Common Lisp 包含一些允許修改列表結構的函數。為了提高效率,這些函數是具有破壞性的。雖然它們可以回收利用作為參數傳給它們的?`cons`?,但并不是因為想要它們的副作用而調用它們 (**譯者注:**因為這些函數的副作用并沒有任何保證,下面的例子將說明問題)。
比如,?`delete`?是?`remove`?的一個具有破壞性的版本。雖然它可以破壞作為參數傳給它的列表,但它并不保證什么。在大多數的 Common Lisp 的實現中,會出現下面的情況:
~~~
> (setf lst '(a r a b i a) )
(A R A B I A)
> (delete 'a lst )
(R B I)
> lst
(A R B I)
~~~
正如?`remove`?一樣,如果你想要副作用,應該對返回值使用?`setf`?:
~~~
(setf lst (delete 'a lst))
~~~
破壞性函數是怎樣回收利用傳給它們的列表的呢?比如,可以考慮?`nconc`?——?`append`?的破壞性版本。[2]下面是兩個參數版本的實現,其清楚地展示了兩個已知列表是怎樣被縫在一起的:
~~~
(defun nconc2 ( x y)
(if (consp x)
(progn
(setf (cdr (last x)) y)
x)
y))
~~~
我們找到第一個列表的最后一個?*Cons*?核 (cons cells),把它的?`cdr`?設置成指向第二個列表。一個正規的多參數的?`nconc`?可以被定義成像附錄 B 中的那樣。
函數?`mapcan`?類似?`mapcar`?,但它是用?`nconc`?把函數的返回值 (必須是列表) 拼接在一起的:
~~~
> (mapcan #'list
'(a b c)
'(1 2 3 4))
( A 1 B 2 C 3)
~~~
這個函數可以定義如下:
~~~
(defun our-mapcan (fn &rest lsts )
(apply #'nconc (apply #'mapcar fn lsts)))
~~~
使用?`mapcan`?時要謹慎,因為它具有破壞性。它用?`nconc`?拼接返回的列表,所以這些列表最好不要再在其它地方使用。
這類函數在處理某些問題的時候特別有用,比如,收集樹在某層上的所有子結點。如果?`children`?函數返回一個節點的孩子節點的列表,那么我們可以定義一個函數返回某節點的孫子節點的列表如下:
~~~
(defun grandchildren (x)
(mapcan #'(lambda (c)
(copy-list (children c)))
(children x)))
~~~
這個函數調用?`copy-list`?時存在一個假設 ——?`chlidren`?函數返回的是一個已經保存在某個地方的列表,而不是構建了一個新的列表。
一個?`mapcan`?的無損變體可以這樣定義:
~~~
(defun mappend (fn &rest lsts )
(apply #'append (apply #'mapcar fn lsts)))
~~~
如果使用?`mappend`?函數,那么?`grandchildren`?的定義就可以省去?`copy-list`?:
~~~
(defun grandchildren (x)
(mappend #'children (children x)))
~~~
## 12.5 示例:二叉搜索樹 (Example: Binary Search Trees)[](http://acl.readthedocs.org/en/latest/zhCN/ch12-cn.html#example-binary-search-trees "Permalink to this headline")
在某些情況下,使用破壞性操作比使用非破壞性的顯得更自然。第 4.7 節中展示了如何維護一個具有二分搜索格式的有序對象集 (或者說維護一個[二叉搜索樹 (BST)](http://zh.wikipedia.org/zh-cn/%E4%BA%8C%E5%85%83%E6%90%9C%E5%B0%8B%E6%A8%B9))。第 4.7 節中給出的函數都是非破壞性的,但在我們真正使用BST的時候,這是一個不必要的保護措施。本節將展示如何定義更符合實際應用的具有破壞性的插入函數和刪除函數。
圖 12.8 展示了如何定義一個具有破壞性的?`bst-insert`?(第 72 頁「**譯者注:**第 4.7 節」)。相同的輸入參數,能夠得到相同返回值。唯一的區別是,它將修改作為第二個參數輸入的 BST。 在第 2.12 節中說過,具有破壞性并不意味著一個函數調用具有副作用。的確如此,如果你想使用?`bst-insert!`?構造一個 BST,你必須像調用?`bst-insert`?那樣調用它:
~~~
> (setf *bst* nil)
NIL
> (dolist (x '(7 2 9 8 4 1 5 12))
(setf *bst* (bst-insert! x *bst* #'<)))
NIL
~~~
~~~
(defun bst-insert! (obj bst <)
(if (null bst)
(make-node :elt obj)
(progn (bsti obj bst <)
bst)))
(defun bsti (obj bst <)
(let ((elt (node-elt bst)))
(if (eql obj elt)
bst
(if (funcall < obj elt)
(let ((l (node-l bst)))
(if l
(bsti obj l <)
(setf (node-l bst)
(make-node :elt obj))))
(let ((r (node-r bst)))
(if r
(bsti obj r <)
(setf (node-r bst)
(make-node :elt obj))))))))
~~~
**圖 12.8: 二叉搜索樹:破壞性插入**
你也可以為 BST 定義一個類似 push 的功能,但這超出了本書的范圍。(好奇的話,可以參考第 409 頁 「**譯者注:**即備注 204 」 的宏定義。)
與?`bst-remove`?(第 74 頁「**譯者注:**第 4.7 節」) 對應,圖 12.9 展示了一個破壞性版本的?`bst-delete`?。同?`delete`?一樣,我們調用它并不是因為它的副作用。你應該像調用?`bst-remove`?那樣調用?`bst-delete`?:
~~~
> (setf *bst* (bst-delete 2 *bst* #'<) )
#<7>
> (bst-find 2 *bst* #'<)
NIL
~~~
~~~
(defun bst-delete (obj bst <)
(if bst (bstd obj bst nil nil <))
bst)
(defun bstd (obj bst prev dir <)
(let ((elt (node-elt bst)))
(if (eql elt obj)
(let ((rest (percolate! bst)))
(case dir
(:l (setf (node-l prev) rest))
(:r (setf (node-r prev) rest))))
(if (funcall < obj elt)
(if (node-l bst)
(bstd obj (node-l bst) bst :l <))
(if (node-r bst)
(bstd obj (node-r bst) bst :r <))))))
(defun percolate! (bst)
(cond ((null (node-l bst))
(if (null (node-r bst))
nil
(rperc! bst)))
((null (node-r bst)) (lperc! bst))
(t (if (zerop (random 2))
(lperc! bst)
(rperc! bst)))))
(defun lperc! (bst)
(setf (node-elt bst) (node-elt (node-l bst)))
(percolate! (node-l bst)))
(defun rperc! (bst)
(setf (node-elt bst) (node-elt (node-r bst)))
(percolate! (node-r bst)))
~~~
**圖 12.9: 二叉搜索樹:破壞性刪除**
**譯注:**?此范例已被回報為錯誤的,一個修復的版本請造訪[這里](https://gist.github.com/2868339)。
## 12.6 示例:雙向鏈表 (Example: Doubly-Linked Lists)[](http://acl.readthedocs.org/en/latest/zhCN/ch12-cn.html#example-doubly-linked-lists "Permalink to this headline")
普通的 Lisp 列表是單向鏈表,這意味著其指針指向一個方向:我們可以獲取下一個元素,但不能獲取前一個。在[雙向鏈表](http://zh.wikipedia.org/wiki/%E5%8F%8C%E5%90%91%E9%93%BE%E8%A1%A8)中,指針指向兩個方向,我們獲取前一個元素和下一個元素都很容易。這一節將介紹如何創建和操作雙向鏈表。
圖 12.10 展示了如何用結構來實現雙向鏈表。將?`cons`?看成一種結構,它有兩個字段:指向數據的?`car`?和指向下一個元素的?`cdr`?。要實現一個雙向鏈表,我們需要第三個字段,用來指向前一個元素。圖 12.10 中的?`defstruct`?定義了一個含有三個字段的對象?`dl`?(用于“雙向鏈接”),我們將用它來構造雙向鏈表。`dl`?的?`data`?字段對應一個?`cons`?的?`car`,`next`?字段對應?`cdr`?。?`prev`?字段就類似一個`cdr`?,指向另外一個方向。(圖 12.11 是一個含有三個元素的雙向鏈表。) 空的雙向鏈表為?`nil`?,就像空的列表一樣。
~~~
(defstruct (dl (:print-function print-dl))
prev data next)
(defun print-dl (dl stream depth)
(declare (ignore depth))
(format stream "#<DL ~A>" (dl->list dl)))
(defun dl->list (lst)
(if (dl-p lst)
(cons (dl-data lst) (dl->list (dl-next lst)))
lst))
(defun dl-insert (x lst)
(let ((elt (make-dl :data x :next lst)))
(when (dl-p lst)
(if (dl-prev lst)
(setf (dl-next (dl-prev lst)) elt
(dl-prev elt) (dl-prev lst)))
(setf (dl-prev lst) elt))
elt))
(defun dl-list (&rest args)
(reduce #'dl-insert args
:from-end t :initial-value nil))
(defun dl-remove (lst)
(if (dl-prev lst)
(setf (dl-next (dl-prev lst)) (dl-next lst)))
(if (dl-next lst)
(setf (dl-prev (dl-next lst)) (dl-prev lst)))
(dl-next lst))
~~~
**圖 12.10: 構造雙向鏈表**
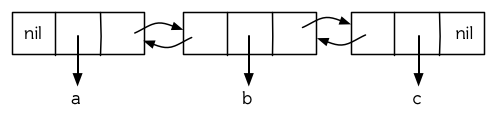
**圖 12.11: 一個雙向鏈表。**
為了便于操作,我們為雙向鏈表定義了一些實現類似?`car`?,?`cdr`?,?`consp`?功能的函數:`dl-data`?,?`dl-next`?和?`dl-p`?。?`dl->list`是?`dl`?的打印函數(`print-function`),其返回一個包含?`dl`?所有元素的普通列表。
函數?`dl-insert`?就像針對雙向鏈表的?`cons`?操作。至少,它就像?`cons`?一樣,是一個基本構建函數。與?`cons`?不同的是,它實際上要修改作為第二個參數傳遞給它的雙向鏈表。在這種情況下,這是自然而然的。我們?`cons`?內容到普通列表前面,不需要對普通列表的`rest`?(**譯者注:**?`rest`?即?`cdr`?的另一種表示方法,這里的?`rest`?是對通過?`cons`?構建后列表來說的,即修改之前的列表) 做任何修改。但是要在雙向鏈表的前面插入元素,我們不得不修改列表的?`rest`?(這里的?`rest`?即指沒修改之前的雙向鏈表) 的?`prev`?字段來指向這個新元素。
幾個普通列表可以共享同一個尾端。因為雙向鏈表的尾端不得不指向它的前一個元素,所以不可能存在兩個雙向鏈表共享同一個尾端。如果?`dl-insert`?不具有破壞性,那么它不得不復制其第二個參數。
單向鏈表(普通列表)和雙向鏈表另一個有趣的區別是,如何持有它們。我們使用普通列表的首端,來表示單向鏈表,如果將列表賦值給一個變量,變量可以通過保存指向列表第一個?`cons`?的指針來持有列表。但是雙向鏈表是雙向指向的,我們可以用任何一個點來持有雙向鏈表。?`dl-insert`?另一個不同于?`cons`?的地方在于?`dl-insert`?可以在雙向鏈表的任何位置插入新元素,而?`cons`?只能在列表的首端插入。
函數?`dl-list`?是對于?`dl`?的類似?`list`?的功能。它接受任意多個參數,它會返回一個包含以這些參數作為元素的?`dl`?:
~~~
> (dl-list 'a 'b 'c)
#<DL (A B C)>
~~~
它使用了?`reduce`?函數 (并設置其?`from-end`?參數為?`true`,`initial-value`?為?`nil`),其功能等價于
~~~
(dl-insert 'a (dl-insert 'b (dl-insert 'c nil)) )
~~~
如果將?`dl-list`?定義中的?`#'dl-insert`?換成?`#'cons`,它就相當于?`list`?函數了。下面是?`dl-list`?的一些常見用法:
~~~
> (setf dl (dl-list 'a 'b))
#<DL (A B)>
> (setf dl (dl-insert 'c dl))
#<DL (C A B)>
> (dl-insert 'r (dl-next dl))
#<DL (R A B)>
> dl
#<DL (C R A B)>
~~~
最后,`dl-remove`?的作用是從雙向鏈表中移除一個元素。同?`dl-insert`?一樣,它也是具有破壞性的。
## 12.7 環狀結構 (Circular Structure)[](http://acl.readthedocs.org/en/latest/zhCN/ch12-cn.html#circular-structure "Permalink to this headline")
將列表結構稍微修改一下,就可以得到一個環形列表。存在兩種環形列表。最常用的一種是其頂層列表結構是一個環的,我們把它叫做?`cdr-circular`?,因為環是由一個?`cons`?的?`cdr`?構成的。
構造一個單元素的?`cdr-circular`?列表,可以將一個列表的?`cdr`?設置成列表自身:
~~~
> (setf x (list 'a))
(A)
> (progn (setf (cdr x) x) nil)
NIL
~~~
這樣?`x`?就是一個環形列表,其結構如圖 12.12 (左) 所示。
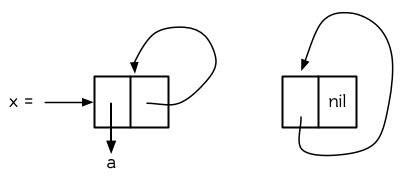
**圖 12.12 環狀列表。**
如果 Lisp 試著打印我們剛剛構造的結構,將會顯示 (a a a a a …… —— 無限個?`a`)。但如果設置全局變量?`*print-circle*`?為?`t`?的話,Lisp 就會采用一種方式打印出一個能代表環形結構的對象:
~~~
> (setf *print-circle* t )
T
> x
#1=(A . #1#)
~~~
如果你需要,你也可以使用?`#n=`?和?`#n#`?這兩個讀取宏,來自己表示共享結構。
`cdr-cicular`?列表十分有用,比如,可以用來表示緩沖區、池。下面這個函數,可以將一個普通的非空列表,轉換成一個對應的`cdr-cicular`?列表:
~~~
(defun circular (lst)
(setf (cdr (last lst)) lst))
~~~
另外一種環狀列表叫做?`car-circular`?列表。`car-circular`?列表是一個樹,并將其自身當作自己的子樹的結構。因為環是通過一個`cons`?的?`car`?形成的,所以叫做?`car-circular`。這里構造了一個?`car-circular`?,它的第二個元素是它自身:
~~~
> (let ((y (list 'a )))
(setf (car y) y)
y)
#i=(#i#)
~~~
圖 12.12 (右) 展示了其結構。這個?`car-circular`?是一個正規列表。?`cdr-circular`?列表都不是正規列表,除開一些特殊情況?`car-circular`?列表是正規列表。
一個列表也可以既是?`car-circular`?,又是?`cdr-circular`?。 一個?`cons`?的?`car`?和?`cdr`?均是其自身:
~~~
> (let ((c (cons 11)) )
(setf (car c) c
(cdr c) c)
c)
#1=(#1# . #1#)
~~~
很難想像這樣的一個列表有什么用。實際上,了解環形列表的主要目的就是為了避免因為偶然因素構造出了環形列表,因為,將一個環形列表傳給一個函數,如果該函數遍歷這個環形列表,它將進入死循環。
環形結構的這種問題在列表以外的其他對象中也存在。比如,一個數組可以將數組自身當作其元素:
~~~
> (setf *print-array* t )
T
> (let ((a (make-array 1)) )
(setf (aref a 0) a)
a)
#1=#(#1#)
~~~
實際上,任何可以包含元素的對象都可能包含其自身作為元素。
用?`defstruct`?構造出環形結構是相當常見的。比如,一個結構?`c`?是一顆樹的元素,它的?`parent`?字段所指向的結構?`p`?的?`child`?字段也恰好指向?`c`?。
~~~
> (progn (defstruct elt
(parent nil ) (child nil) )
(let ((c (make-elt) )
(p (make-elt)) )
(setf (elt-parent c) p
(elt-child p) c)
c) )
#1=#S(ELT PARENT #S(ELT PARENT NIL CHILD #1#) CHILD NIL)
~~~
要實現像這樣一個結構的打印函數 (`print-function`),我們需要將全局變量?`*print-circle*`?綁定為?`t`?,或者避免打印可能構成環的字段。
## 12.8 常量結構 (Constant Structure)[](http://acl.readthedocs.org/en/latest/zhCN/ch12-cn.html#constant-structure "Permalink to this headline")
因為常量實際上是程序代碼的一部分,所以我們也不應該修改他們,或者是不經意地寫了自重寫的代碼。一個通過?`quote`?引用的列表是一個常量,所以一定要小心,不要修改被引用的列表的任何?`cons`。比如,如果我們用下面的代碼,來測試一個符號是不是算術運算符:
~~~
(defun arith-op (x)
(member x '(+ - * /)))
~~~
如果被測試的符號是算術運算符,它的返回值將至少一個被引用列表的一部分。如果我們修改了其返回值,
~~~
> (nconc (arith-op '*) '(as i t were))
(* / AS IT WERE)
~~~
那么我就會修改?`arith-op`?函數中的一個列表,從而改變了這個函數的功能:
~~~
> (arith-op 'as )
(AS IT WERE)
~~~
寫一個返回常量結構的函數,并不一定是錯誤的。但當你考慮使用一個破壞性的操作是否安全的時候,你必須考慮到這一點。
有幾個其它方法來實現?`arith-op`,使其不返回被引用列表的部分。一般地,我們可以通過將其中的所有引用(?`quote`?) 替換成?`list`來確保安全,這使得它每次被調用都將返回一個新的列表:
~~~
(defun arith-op (x)
(member x (list '+ '- '* '/)))
~~~
這里,使用?`list`?是一種低效的解決方案,我們應該使用?`find`?來替代?`member`:
~~~
(defun arith-op (x)
(find x '(+ - * /)))
~~~
這一節討論的問題似乎只與列表有關,但實際上,這個問題存在于任何復雜的對象中:數組,字符串,結構,實例等。你不應該逐字地去修改程序的代碼段。
即使你想寫自修改程序,通過修改常量來實現并不是個好辦法。編譯器將常量編譯成了代碼,破壞性的操作可能修改它們的參數,但這些都是沒有任何保證的事情。如果你想寫自修改程序,正確的方法是使用閉包 (見 6.5 節)。
## Chapter 12 總結 (Summary)[](http://acl.readthedocs.org/en/latest/zhCN/ch12-cn.html#chapter-12-summary "Permalink to this headline")
1. 兩個列表可以共享一個尾端。多個列表可以以樹的形式共享結構,而不是共享頂層列表結構。可通過拷貝方式來避免共用結構。
2. 共享結構通常可以被忽略,但如果你要修改列表,則需要特別注意。因為修改一個含共享結構的列表可能修改所有共享該結構的列表。
3. 隊列可以被表示成一個?`cons`?,其的?`car`?指向隊列的第一個元素,?`cdr`?指向隊列的最后一個元素。
4. 為了提高效率,破壞性函數允許修改其輸入參數。
5. 在某些應用中,破壞性的實現更適用。
6. 列表可以是?`car-circular`?或?`cdr-circular`?。 Lisp 可以表示圓形結構和共享結構。
7. 不應該去修改的程序代碼段中的常量形式。
## Chapter 12 練習 (Exercises)[](http://acl.readthedocs.org/en/latest/zhCN/ch12-cn.html#chapter-12-exercises "Permalink to this headline")
1. 畫三個不同的樹,能夠被打印成?`((A)?(A)?(A))`?。寫一個表達式來生成它們。
2. 假設?`make-queue`?,?`enqueue`?和?`dequeue`?是按照圖 12.7 中的定義,用箱子表式法畫出下面每一步所得到的隊列的結構圖:
~~~
> (setf q (make-queue))
(NIL)
> (enqueue 'a q)
(A)
> (enqueue 'b q)
(A B)
> (dequeue q)
A
~~~
1. 定義一個函數?`copy-queue`?,可以返回一個 queue 的拷貝。
2. 定義一個函數,接受兩個輸入參數?`object`?和?`queue`?,能將?`object`?插入到?`queue`?的首端。
3. 定義一個函數,接受兩個輸入參數?`object`?和?`queue`,能具有破壞性地將?`object`?的第一個實例 (?`eql`?等價地) 移到?`queue`?的首端。
4. 定義一個函數,接受兩個輸入參數?`object`?和?`lst`?(?`lst`?可能是?`cdr-circular`?列表),如果?`object`?是?`lst`?的成員時返回真。
5. 定義一個函數,如果它的參數是一個?`cdr-circular`?則返回真。
6. 定義一個函數,如果它的參數是一個?`car-circular`?則返回真。
腳注
[1] | 比如,在 Common Lisp 中,修改一個被用作符號名的字符串被認為是一種錯誤,因為內部的定義并沒聲明它是從參數復制來的,所以必須假定修改傳入內部的任何參數中的字符串來創建新的符號是錯誤的。
[2] | 函數名稱中 n 的含義是 “non-consing”。一些具有破壞性的函數以 n 開頭。
