## **小灰的算法之旅**
數據結構大致包含以下幾種存儲結構:
**線性表**:零個或多個數據元素的**有限序列**
還可細分為順序表(底層實現靠數組)、鏈表、棧和隊列;棧和隊列隸屬于線性表,是特殊的線性表。
元素有多個時,第一個元素無前驅,最后一個無后繼,其他每個元素都有且只有一個前驅和后繼。
**樹結構**:包括普通樹,二叉樹,線索二叉樹等;
**圖存儲結構**;
## **數組、順序表(順序存儲結構)**
順序存儲:一段地址連續的存儲單元依次存儲線性表的數據元素。
### **三個重要屬性:**
起始位置、最大存儲容量、當前長度
查詢的時間復雜度 o(1)
插入和刪除的復雜度是o(n)。 ?
插入時,后面的數據都要往后移動,刪除時,后面的數據都要往前移動
### **優點:**
l可以快速的存取表中任一位置的元素。
l不需要為表示元素之間的邏輯關系而增加額外存儲空間。
### **缺點:**
l插入和刪除操作需要移動大量元素、性能受損
l當元素數量變化較大,難以確定最大存儲容量
l造成存儲空間的“碎片”
順序表底層就是使用數組。
## **鏈表、鏈式存儲結構**
鏈式存儲:地址可以連續也可以不連續的存儲單元存儲數據元素
數據域:存儲數據元素信息的域
指針域:存儲直接后繼位置的域(后一個元素的地址)
**數據域 + 指針域 ?就是****結點**
### **單鏈表**
單鏈表:鏈表中的每個結點中只包含一個指針域
頭指針:鏈表中第一個結點的存儲位置
頭結點:有時會為了方便,會在單鏈表的第一個結點前附設一個節點,就是頭結點,頭結點的數據域可以不存儲任何信息。
頭指針和頭結點的區別:
頭指針是指鏈表指向第一個結點的指針,若鏈表有頭結點,則是指向頭結點的指針
頭指針具有標識作用,所以常用頭指針冠以鏈表的名字
無論鏈表是否為空,頭指針均不為空。頭指針是鏈表的必要元素
頭結點是為了操作的統一和方便而設立的,放在第一個元素的結點之前,其數據域一般無意義。
有了頭結點,對在第一個元素節點前插入結點和刪除第一個結點,其操作與其他結點的操作就統一了。
頭結點不一定是鏈表必須要素
查詢的時間復雜度 o(1)到o(n) ,查第一個就是o(1),最壞的情況是 o(n)
插入和刪除的復雜度,當知道元素的指針位置時是o(1),否則需要先查詢,復雜度則變成o(n)。 ?
插入和刪除越頻繁的操作,單鏈表的效率優勢就越是明顯。
工作指針后移
### **順序存儲結構和單鏈表存儲結構的區別**
存儲分配方式:
順序存儲結構用一段連續的存儲單元依次存儲線性表的數據元素。
單鏈表采用鏈式存儲結構,用一組任意的存儲單元存放線性表的元素。
時間性能:
查找:
順序存儲結構O(1)
單鏈表O(n)
插入和刪除
順序存儲結構需要平均移動表長一半的元素,時間為O(n)
單鏈表在線出某位置的指針后,插入和刪除時間僅為O(1)
空間性能
順序存儲需要預分配存儲空間,分大了浪費,分小了易發生上溢
單鏈表不需要分配存儲空間,只要有就可以分配,元素個數也不受限制
結論:
**插入和刪除頻繁的使用單鏈表結構,頻繁查找的使用順序存儲結構**
**元素個數變化較大或根本無法確定可能的個數范圍,最好考慮單鏈表,這樣不需要考慮存儲空間的大小**
### **靜態鏈表**
注:Java不需要靜態列表
靜態鏈表其實是為了給沒有指針的高級語言設計的一種實現單鏈表能力的方法。
首先我們讓數組的元素都是由兩個數據域組成, data和cur。也就是說,數組的每個下標都對應一個data和一個cur。數據域data,用來存放數據元素,也就是通常我們要處理的數據;而游標cur相當于單鏈表中的next指針,存放該元素的后繼在數組的下標
這種用數組描述的鏈表叫做靜態鏈表,這種描述方法還有起名叫做游標實現法
為了方便插入數據,通常把數組建立的大一些,防止溢出。另外數組的第一個和最后一個元素作為特殊元素,不存數據。未被使用的數組元素叫做備用鏈表。而數組第一個元素,即下標為0的元素的cur,就存放備用鏈表的第一個結點的下標;而數組的最后一個元素的cur則存放第一個有數值的元素的下標,相當于單鏈表中的頭結點作用,當整個鏈表為空時,則為02
### **循環鏈表**
將單鏈表中終端結點的指針端由空指針改為指向頭結點,就使整個單鏈表形成一個環,這種頭尾相接的單鏈表稱為單循環鏈表,簡稱循環鏈表。
為了使空鏈表和非空鏈表處理一致,通常會設一個頭結點。
循環鏈表和單鏈表主要差異在循環的判斷條件上,原來是判斷p->next是否為空,現在則是p->next不等于頭結點,則循環未結束。
### **雙向鏈表**
雙向鏈表(double linked list)是在單鏈表的每個結點中,再設置一個指向其前驅結點的指針域。所以在雙向鏈表中的結點都有兩個指針域,一個指向直接后繼,另一個指向直接前驅。
插入和刪除時需要更改兩個指針變量。
## **棧**
棧是限定僅在表尾進行插入和刪除操作的線性表。
我們把**允許插入和刪除的一端稱為棧頂**(top),另一端稱為棧底(bottom),不含任何數據元素的棧稱為空棧。棧又稱為后進先出(Last In First Out)的線性表,簡稱LIFO結構。
棧元素也具有線性關系,棧是一種特殊的線性表。定義中說是在線性表的表尾插入和刪除操作,這里表尾是指棧頂,而不是棧底。特殊在于限制了這個線性表的插入和刪除位置,只在棧頂進行。
棧的插入操作,叫作進棧,也稱壓棧、入棧。類似子彈入彈夾。
棧的刪除操作,叫作出棧,也有的叫作彈棧。如同彈夾中的子彈出夾。
## **隊列**
隊列是**只允許在一端進行插入操作、而在另一端進行刪除操作的線性表。**
隊列是一種先進先出(First In First Out)的線性表,簡稱FIFO,允許插入的一端稱為隊尾,允許刪除的一端稱為隊頭。
同樣是線性表,隊列也有類似線性表的各種操作,不同的就是插入數據只能在隊,尾進行,刪除數據只能在隊頭進行。
把隊列的這種頭尾相接的順序存儲結構稱為循環隊列。隊尾指針指向的位置永遠空出1位,所以隊列
最大容量比數組長度小1。
隊列的鏈式存儲結構,其實就是線性表的單鏈表,只不過它只能尾進頭出而已,我們把它簡稱為鏈隊列。
**雙端隊列**: 這種數據結構,可以說綜合了棧和隊列的優點,對雙端隊列來說,從隊頭一端可以入隊或出隊,從隊尾一端也可以入隊或出隊。盡管雙端隊列看起來似乎比棧和隊列更靈活,但**實際上在應用程序中遠不及棧和隊列有用。**
**優先隊列:**??優先隊列已經不屬于線性數據結構的范疇了,它是基于二叉堆來實現
## **hash 哈希 (散列表)**
散列表也叫作哈希表 (hash table),這種數據結構提供了**鍵(Key)和值(Value) 的映射關系。**
**底層**使用**數組**, 通過**哈希函數將 key 轉為 數組下標**
當數據量大時, 容易出現哈希函數將不同的key 轉為數組**下標**時出現**相同**的值, 這就是**哈希沖突**
哈希沖突的解決:
**開放尋址法**:如果經過哈希函數獲得的下標所在位置已經有值,則往后移動一位,如果移動到的位置也已經有值了,就繼續往后移動,直到找到空位。開放尋址法有多種,這是最簡單的,java 的 ThreadLocal 就是這樣做的。
**鏈表法(拉鏈法)**:如果經過哈希函數獲得的下標所在位置已經有值,則在這個位置增加一個鏈表,這個位置所有的數據以key value 的對象形式都放到鏈表里,相當于數組嵌套鏈表。java的HashMap是這樣做的(1.8以后應該是紅黑樹)
hash 的擴容
對于JDK中的散列表實現類HashMap來說,影響其擴容的因素有兩個。
Capacity ,即HashMap的當前長度
LoadFactor ,即HashMap的負載因子,默認值為0.75f
HashMap.Size >= Capacity×LoadFactor
hash 擴容過程
擴容 ,創建一個新的Entry空數組,長度是原數組的2倍。
重新Hash ,遍歷原Entry數組,把所有的Entry重新Hash到新數組中。為什么要重新Hash呢?因為長度擴大以后,Hash的規則也隨之改變。
經過擴容,原本擁擠的散列表重新變得稀疏,原有的Entry也重新得到了盡可能均勻的分配。
## **樹**
在數據結構中,樹的定義如下。
樹(tree)是n(n≥0)個節點的有限集。當n=0時,稱為空樹。在任意一 個非空樹中,有如下特點。
1.有且僅有一個特定的稱為根的節點。
2.當n>1時,其余節點可分為m(m>0)個互不相交的有限集,每一個集 合本身又是一個樹,并稱為根的子樹。 下面這張圖,就是一個標準的樹結構。
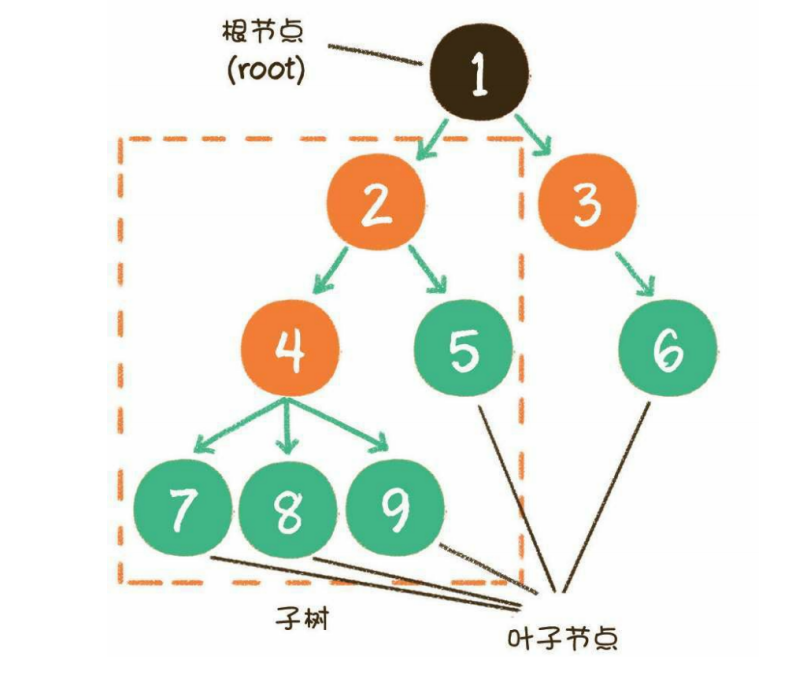
在上圖中,節點1是根節點(root) ;節點5、6、7、8是樹的末端,沒 有“孩子”,被稱為葉子節點(leaf) 。圖中的虛線部分,是根節點1的 其中一個子樹 。
@font-face{ font-family:"Times New Roman"; } @font-face{ font-family:"宋體"; } @font-face{ font-family:"Calibri"; } @list l0:level1{ mso-level-number-format:decimal; mso-level-suffix:space; mso-level-text:"%1."; mso-level-tab-stop:none; mso-level-number-position:left; margin-left:0.0000pt; text-indent:0.0000pt; font-family:'Times New Roman';} p.MsoNormal{ mso-style-name:正文; mso-style-parent:""; margin:0pt; margin-bottom:.0001pt; mso-pagination:none; text-align:justify; text-justify:inter-ideograph; font-family:Calibri; mso-fareast-font-family:宋體; mso-bidi-font-family:'Times New Roman'; font-size:10.5000pt; mso-font-kerning:1.0000pt; } h3{ mso-style-name:"標題 3"; mso-style-noshow:yes; mso-style-next:正文; margin-top:13.0000pt; margin-bottom:13.0000pt; mso-para-margin-top:0.0000gd; mso-para-margin-bottom:0.0000gd; page-break-after:avoid; mso-pagination:lines-together; text-align:justify; text-justify:inter-ideograph; mso-outline-level:3; line-height:172%; font-family:Calibri; mso-fareast-font-family:宋體; mso-bidi-font-family:'Times New Roman'; font-weight:bold; font-size:16.0000pt; mso-font-kerning:1.0000pt; } span.msoIns{ mso-style-type:export-only; mso-style-name:""; text-decoration:underline; text-underline:single; color:blue; } span.msoDel{ mso-style-type:export-only; mso-style-name:""; text-decoration:line-through; color:red; } @page{mso-page-border-surround-header:no; mso-page-border-surround-footer:no;}@page Section0{ } div.Section0{page:Section0;}
二叉查找樹 利于查找和排序,但 9 ?8 ?7 ?6 ?5 ?等節點樹時會涉及二叉樹的自平衡,二叉樹自平衡的 方式有多種,如紅黑樹、AVL樹、樹堆等。
**二叉樹的遍歷**
1\. 深度優先遍歷 (前序遍歷、中序遍歷、后序遍歷)。
2\. 廣度優先遍歷 (層序遍歷)。
**深度優先遍歷**
二叉樹前序遍歷、中序遍歷、后序遍歷、層序遍歷的直觀理解 https://blog.csdn.net/u013834525/article/details/80421684
(前序遍歷、中序遍歷、后序遍歷) 指的是 輸出根節點的順序
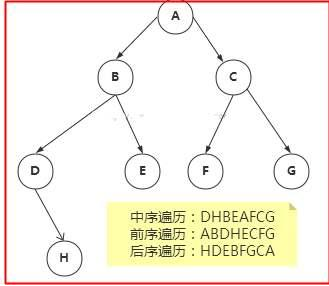
二叉樹的**前序遍歷**,輸出順序是根節點、左子樹、右子樹。
輸出順序 ??根 =》左 \=》右
1\. 從樹的根節點開始輸出根節點,然后一直遍歷并輸出左子樹的左節點,直到節點沒有左子樹為止,這時候再去遍歷最后一個左節點的右子樹或者父節點的右子樹
2\. 遍歷右子樹時, 有左子樹的,再按照1的流程遍歷輸出這個右子樹。
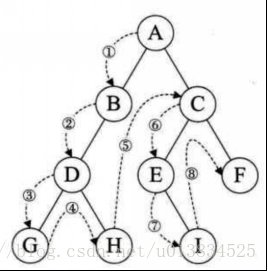
二叉樹的中序遍歷,輸出順序是左子樹、根節點、右子樹。
輸出順序 ??左 =》根 \=》右
1.首先訪問根節點的左孩子,如果這個左孩子還擁有左孩子,則繼續深 入訪問下去,一直找到不再有左孩子的節點,并輸出該節點。
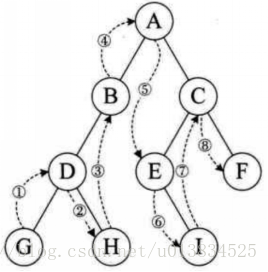
二叉樹的**后序遍歷**,輸出順序是根節點、左子樹、右子樹。
輸出順序 ??左 =》右 \=》根
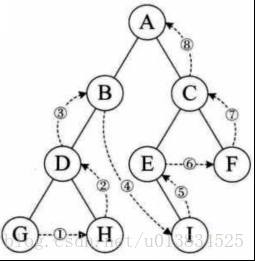
**廣度優先遍歷**
層序遍歷,顧名思義,就是二叉樹按照從根節點到葉子節點的層次關 系,一層一層橫向遍歷各個節點。代碼實現可以使用隊列
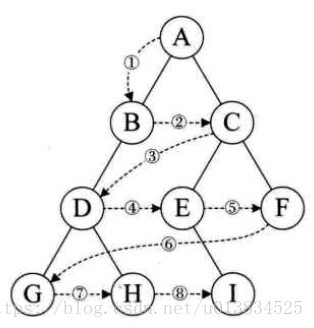
### **二叉堆**
二叉堆本質上是一種完全二叉樹,它分為兩個類型。
1\. 最大堆。
最大堆的任何一個父節點的值,都大于或等于 它 左、右孩子節點的值。
?2. 最小堆。
最小堆的任何一個父節點的值,都小于或等于它左、 右孩子節點的值。
二叉堆的根節點叫作堆頂 。
最大堆的堆頂是整個堆中的最大元素 ;最小堆的堆頂是整個堆中的最小元素 。
堆的刪除操作是單一節點的“下沉”,這兩個操作的平均交換 次數都是堆高度的一半,所以時間復雜度是O(logn)。至于堆的構 建,需要所有非葉子節點依次“下沉”,所以我覺得時間復雜度應該 是O(n)
二叉堆雖然是一個完全二叉 樹,但它的存儲方式并不是鏈式存儲,而是順序存儲。換句話說,二叉 堆的所有節點都存儲在數組中。
假設父節點的下標是parent,那么它的左孩子下標就是 2×parent+1 ;右 孩子下標就是2×parent+2 。
