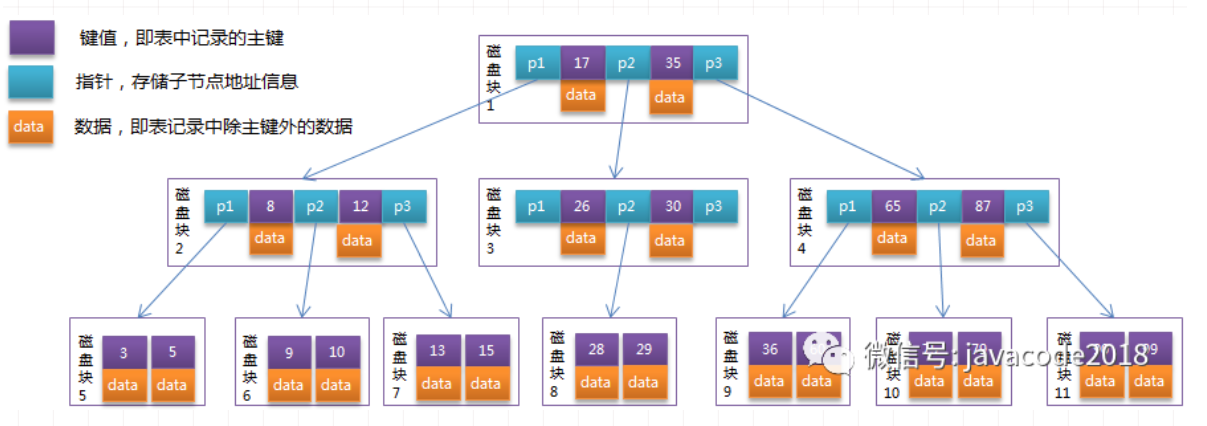
https://zhuanlan.zhihu.com/p/59788528 https://mp.weixin.qq.com/s/wiqfcVrsLgLvLbsTU-qSag ## B樹 一棵m階的B-Tree有如下特性 1. 每個節點最多有m個孩子，m稱為b樹的階 2. 除了根節點和葉子節點外，其它每個節點至少有Ceil(m/2)個孩子 3. 若根節點不是葉子節點，則至少有2個孩子 4. 所有葉子節點都在同一層，且不包含其它關鍵字信息 5. 每個非終端節點包含n個關鍵字（健值）信息 6. 關鍵字的個數n滿足：ceil(m/2)-1 <= n <= m-1 7. ki(i=1,…n)為關鍵字，且關鍵字升序排序 8. Pi(i=1,…n)為指向子樹根節點的指針。P(i-1)指向的子樹的所有節點關鍵字均小于ki，但都大于k(i-1)  每個節點占用一個盤塊的磁盤空間，**一個節點上有兩個升序排序的關鍵字和三個指向子樹根節點的指針，指針存儲的是子節點所在磁盤塊的地址**。兩個鍵將數據劃分成的三個范圍域，對應三個指針指向的子樹的數據的范圍域。以根節點為例，關鍵字為17和35，P1指針指向的子樹的數據范圍為小于17，P2指針指向的子樹的數據范圍為17~35，P3指針指向的子樹的數據范圍為大于35 模擬查找關鍵字29的過程： 1. 根據根節點找到磁盤塊1，讀入內存。【磁盤I/O操作第1次】 2. 比較關鍵字29在區間（17,35），找到磁盤塊1的指針P2 3. 根據P2指針找到磁盤塊3，讀入內存。【磁盤I/O操作第2次】 4. 比較關鍵字29在區間（26,30），找到磁盤塊3的指針P2 5. 根據P2指針找到磁盤塊8，讀入內存。【磁盤I/O操作第3次】 6. 在磁盤塊8中的關鍵字列表中找到關鍵字29 分析上面過程，發現需要3次磁盤I/O操作，和3次內存查找操作，由于內存中的關鍵字是一個有序表結構，可以利用二分法快速定位到目標數據，而3次磁盤I/O操作是影響整個B-Tree查找效率的決定因素。 **B-不利于范圍查找，比如上圖中我們需要查找\[15,36\]區間的數據，需要訪問7個磁盤塊（1/2/7/3/8/4/9），io次數又上去了，范圍查找也是我們經常用到的，所以b-樹也不太適合在磁盤中存儲需要檢索的數據。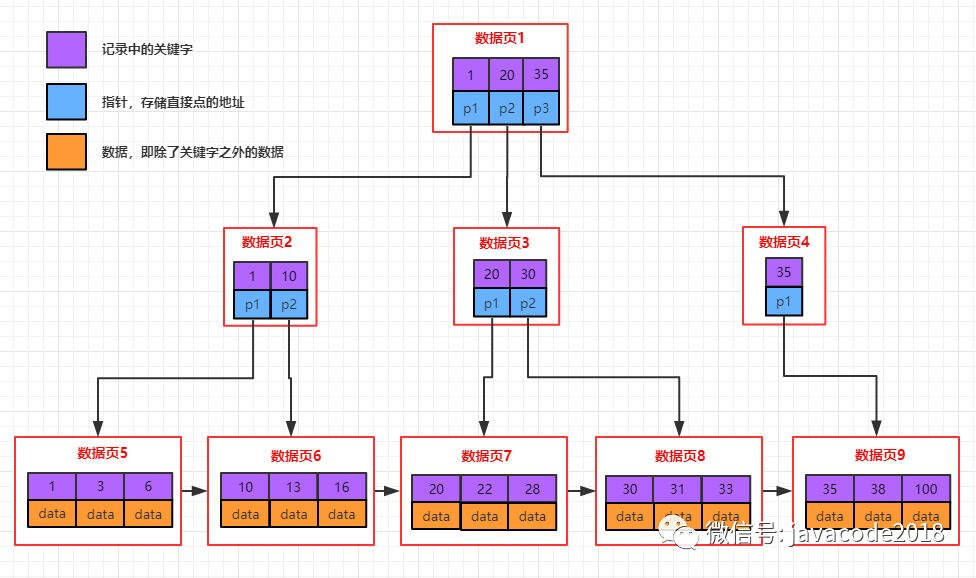** ## B+樹  #### **b+樹的特征** 1.每個結點至多有m個子女 2.除根結點外,每個結點至少有\[m/2\]個子女，根結點至少有兩個子女 3.有k個子女的結點必有k個關鍵字 4.父節點中持有訪問子節點的指針 5.父節點的關鍵字在子節點中都存在（如上面的1/20/35在每層都存在），要么是最小值，要么是最大值，如果節點中關鍵字是升序的方式，父節點的關鍵字是子節點的最小值 6.最底層的節點是葉子節點 7.除葉子節點之外，其他節點不保存數據，只保存關鍵字和指針 8.葉子節點包含了所有數據的關鍵字以及data，葉子節點之間用鏈表連接起來，可以非常方便的支持范圍查找 #### **b+樹與b-樹的幾點不同** ##### **核心區別:** B+樹只有**最底層**的**葉子節點**才**保存數據**，其他的都是非葉子節點，只保存關鍵字和指針，這樣使得**非葉子節點存儲的數據更多**，使樹變矮，這樣內存中可以**存儲更多的指針**，**減少磁盤IO** b+樹中一個節點如果有k個關鍵字，最多可以包含k個子節點（k個關鍵字對應k個指針）；而b-樹對應k+1個子節點（多了一個指向子節點的指針） b+樹除葉子節點之外其他節點值存儲關鍵字和指向子節點的指針，而b-樹還存儲了數據，這樣同樣大小情況下，b+樹可以存儲更多的關鍵字 b+樹葉子節點中存儲了所有關鍵字及data，并且多個節點用鏈表連接，從上圖中看子節點中數據從左向右是有序的，這樣快速可以支撐范圍查找（先定位范圍的最大值和最小值，然后子節點中依靠鏈表遍歷范圍數據） #### **B-Tree和B+Tree該如何選擇？** B-Tree因為非葉子結點也保存具體數據，所以在查找某個關鍵字的時候找到即可返回。而B+Tree所有的數據都在葉子結點，每次查找都得到葉子結點。所以在同樣高度的B-Tree和B+Tree中，B-Tree查找某個關鍵字的效率更高。 由于B+Tree所有的數據都在葉子結點，并且結點之間有指針連接，在找大于某個關鍵字或者小于某個關鍵字的數據的時候，B+Tree只需要找到該關鍵字然后沿著鏈表遍歷就可以了，而B-Tree還需要遍歷該關鍵字結點的根結點去搜索。 由于B-Tree的每個結點（這里的結點可以理解為一個數據頁）都存儲主鍵+實際數據，而B+Tree非葉子結點只存儲關鍵字信息，而每個頁的大小有限是有限的，所以同一頁能存儲的B-Tree的數據會比B+Tree存儲的更少。這樣同樣總量的數據，B-Tree的深度會更大，增大查詢時的磁盤I/O次數，進而影響查詢效率。