# **函數漸近增長:**
分析算法函數增長率是為了體現跟算法函數有關的因素。為算法的復雜度分析做基礎。
概念:給定兩個函數f(n)和g(n),如果存在一個整數N,使得對于所有的n>0,f(n)總是比g(n)大,那么我們說f(n)的增長漸近 快于g(n)。
概念似乎有點艱澀難懂,那接下來我們做幾個測試。
### **1.測試一:假設四個算法的輸入規模都是n:**
1.算法A1要做2n+3次操作,可以這么理解:先執行n次循環,執行完畢后,再有一個n次循環,最后有3次運算;
2.算法A2要做2n次操作;
3.算法B1要做3n+1次操作,可以這個理解:先執行n次循環,再執行一個n次循環,再執行一個n次循環,最后有1 次運算。
4.算法B2要做3n次操作;
那么,上述算法,哪一個更快一些呢?

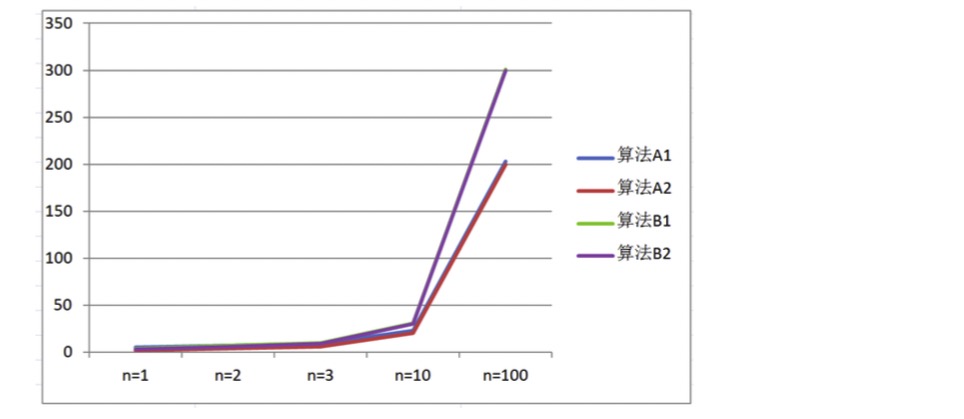
通過數據表格,比較算法A1和算法B1: 當輸入規模n=1時,A1需要執行5次,B1需要執行4次,所以A1的效率比B1的效率低; 當輸入規模n=2時,A1需要執行7次,B1需要執行7次,所以A1的效率和B1的效率一樣; 當輸入規模n>2時,A1需要的執行次數一直比B1需要執行的次數少,所以A1的效率比B1的效率高; 所以我們可以得出結論
當輸入規模n>2時,算法A1的漸近增長小于算法B1 的漸近增長 通過觀察折線圖,我們發現,隨著輸入規模的增大,算法A1和算法A2逐漸重疊到一塊,算法B1和算法B2逐漸重疊
到一塊,所以我們得出結論:
**隨著輸入規模的增大,算法的常數操作可以忽略不計**
### **2.測試二:假設四個算法的輸入規模都是n:**
1.算法C1需要做4n+8次操作
2.算法C2需要做n次操作
3.算法D1需要做2n^2次操作
4.算法D2需要做n^2次操作
那么上述算法,哪個更快一些?
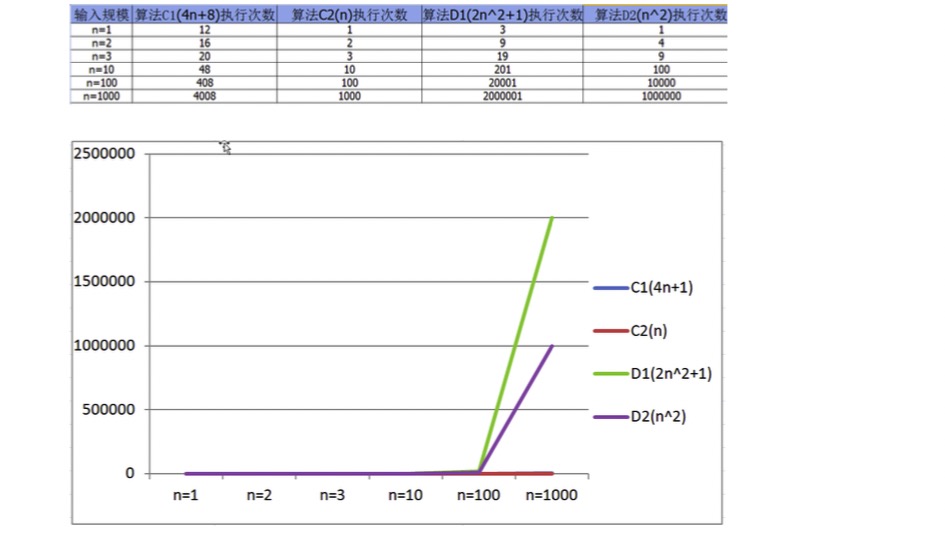
通過數據表格,對比算法C1和算法D1:
當輸入規模n<=3時,算法C1執行次數多于算法D1,因此算法C1效率低一些;
當輸入規模n>3時,算法C1執行次數少于算法D1,因此,算法D2效率低一些,
所以,總體上,算法C1要優于算法D1.
通過折線圖,對比對比算法C1和C2: 隨著輸入規模的增大,算法C1和算法C2幾乎重疊
通過折線圖,對比算法C系列和算法D系列: 隨著輸入規模的增大,即使去除n^2前面的常數因子,D系列的次數要遠遠高于C系列。
因此,可以得出結論:
**隨著輸入規模的增大,與最高次項相乘的常數可以忽略**
### **3.測試三:假設四個算法的輸入規模都是n:**
算法E1: 2n^2+3n+1;
算法E2: n^2
算法F1: 2n^3+3n+1
算法F2: n^3

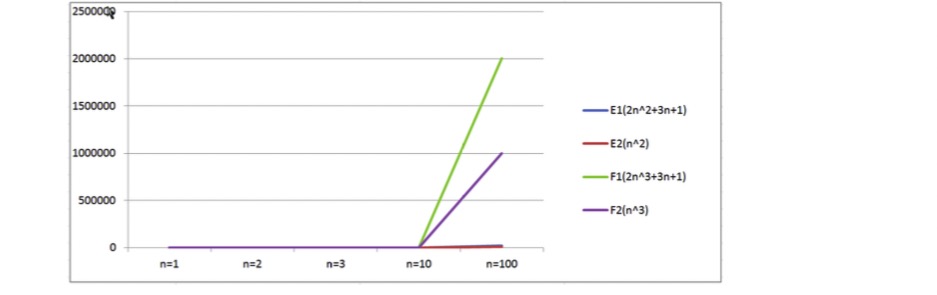
通過數據表格,對比算法E1和算法F1:
當n=1時,算法E1和算法F1的執行次數一樣;
當n>1時,算法E1的執行次數遠遠小于算法F1的執行次數;
所以算法E1總體上是由于算法F1的。
通過折線圖我們會看到,算法F系列隨著n的增長會變得特塊,算法E系列隨著n的增長相比較算法F來說,變得比較 慢,所以可以得出結論:
**最高次項的指數大的,隨著n的增長,結果也會變得增長特別快**
### **4.測試四:假設四個算法的輸入規模都是n:**
假設五個算法的輸入規模都是n:
算法G: n^3;
算法H: n^2;
算法I: n:
算法J: logn
算法K: 1
那么上述算法,哪個效率更高呢?

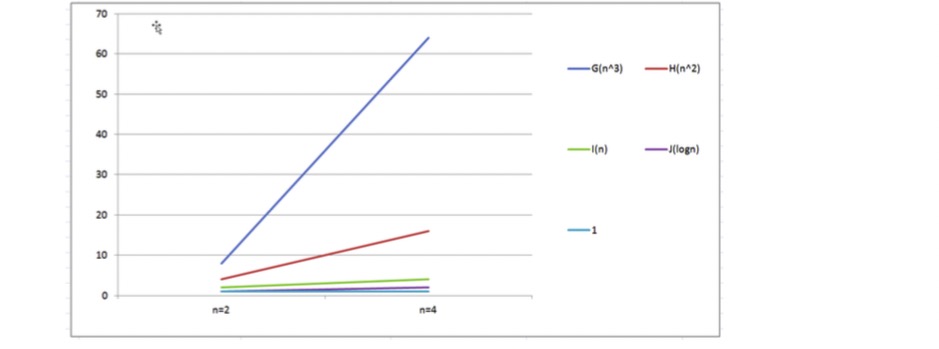
通過觀察數據表格和折線圖,很容易可以得出結論:
**算法函數中n最高次冪越小,算法效率越高 **
總上所述,在我們比較算法隨著輸入規模的增長量時,可以有以下規則:
1.算法函數中的常數可以忽略;
2.算法函數中最高次冪的常數因子可以忽略;
3.算法函數中最高次冪越小,算法效率越高。
