# 算法時間復雜度
算法的時間復雜度就是指算法執行時間多少的意思。
而上一章我們分析了函數的線性增長已經得出了影響算法函數的有關因素
```
1.算法函數中的常數可以忽略;
2.算法函數中最高次冪的常數因子可以忽略;
3.算法函數中最高次冪越小,算法效率越高。
```
所以算法函數越簡單的算法時間復雜度越低。而且我們有一個專業的大O記法來表示算法復雜度。
## **1.大O記法**
**定義:**
在進行算法分析時,語句總的執行次數T(n)是關于問題規模n的函數,進而分析T(n)隨著n的變化情況并確定T(n)的 量級。算法的時間復雜度,就是算法的時間量度,記作:T(n)=O(f(n))。它表示隨著問題規模n的增大,算法執行時間 的增長率和f(n)的增長率相同,稱作算法的漸近時間復雜度,簡稱時間復雜度,其中f(n)是問題規模n的某個函數。
T(n)=O(f(n))
```
n:問題規模
Tn:核心函數執行次數
f(n):核心函數
O():算法時間復雜度的記法
```
在這里,我們需要明確一個事情:**函數執行次數=函數執行時間**
用大寫O()來體現算法時間復雜度的記法,我們稱之為大O記法。一般情況下,隨著輸入規模n的增大,T(n)增長最慢的算法為最優算法。 下面我們使用大O表示法來表示一些求和算法的時間復雜度:
算法一:
```
public function getSum100(){
$sum=0; //1次
$n=100; //2次
$sum = ($n+1)*$n/2 //1次
echo "1到100的和是:".$sum;
}
```
算法二:
```
public function get100Sum(){
$sum=0; //1次
$n=100; //1次
for ($i=1; $i=$n < ; $i++) {
$sum+=$i; //n次
}
echo "1到100的和是:".$sum;
}
```
算法三:
```
static function fun1(){
$sum=0; //1次
$j=100;
for($s = 1;$j<=$n;$s++){
for ($b=1;$b<=$j;$b++) {
$sum +=$b; //n^2次
}
}
}
```
如果忽略判斷條件的執行次數和輸出語句的執行次數,那么當輸入規模為n時,以上算法執行的次數分別為:
**算法一:3次
算法二:n+2次
算法三:n^2+2次**
如果用大O記法表示上述每個算法的時間復雜度,應該如何表示呢?基于我們對函數漸近增長的分析,推導大O階 的表示法有以下幾個規則可以使用:
1.用常數1取代運行時間中的所有加法常數;
2.在修改后的運行次數中,只保留高階項;
3.如果最高階項存在,且常數因子不為1,則去除與這個項相乘的常數;
所以,上述算法的大O記法分別為:
**算法一:O(1)
算法二:O(n)
算法三:O(n^2)
**執行效率:O(1) > O(n) > O(n^2)**
## **2.常見的大O階**
### **2.1線性階**
一般含有非嵌套循環涉及線性階,線性階就是隨著輸入規模的擴大,對應計算次數呈直線增長,例如:
~~~
public function get100Sum(){
$sum=0; //1次
$n=100; //1次
for ($i=1; $i=$n < ; $i++) {
$sum+=$i; //n次
}
echo "1到100的和是:".$sum;
}
~~~
上面這段代碼,它的循環的時間復雜度為O(n),因為循環體中的代碼需要執行n次
### **2.2平方階**
一般嵌套循環屬于這種時間復雜度
~~~
static function fun1(){
$sum=0; //1次
$j=100;
for($s = 1;$j<=$n;$s++){
for ($b=1;$b<=$j;$b++) {
$sum +=$b; //n^2次
}
}
}
~~~
上面這段代碼,n=100,也就是說,外層循環每執行一次,內層循環就執行100次,那總共程序想要從這兩個循環 中出來,就需要執行100\*100次,也就是n的平方次,所以這段代碼的時間復雜度是O(n^2).
### **2.3立方階**
一般三層嵌套循環屬于這種時間復雜度
~~~
static function fun1(){
$sum=0; //1次
$j=100;
for($s = 1;$j<=$n;$s++){
for ($b=1;$b<=$j;$b++) {
for ($a=1;$a<=$j;$a++) {
$sum +=$a; //n^3次
}
}
}
}
~~~
上面這段代碼,n=100,也就是說,外層循環每執行一次,中間循環循環就執行100次,中間循環每執行一次,最 內層循環需要執行100次,那總共程序想要從這三個循環中出來,就需要執行100100100次,也就是n的立方,所 以這段代碼的時間復雜度是O(n^3)
### **2.4 對數階**
~~~
int i=1,n=100;
while(i<n){
i = i*2;
}
~~~
由于每次i\*2之后,就距離n更近一步,假設有x個2相乘后大于n,則會退出循環。由于是2^x=n,得到x=log(2)n,所 以這個循環的時間復雜度為O(logn);
對于對數階,由于隨著輸入規模n的增大,不管底數為多少,他們的增長趨勢是一樣的,所以我們會忽略底數。
### **2.5 常數階**
一般不涉及循環操作的都是常數階,因為它不會隨著n的增長而增加操作次數。例如:
~~~
public function getSum100(){
$n=100; //2次
$sum = ($n+2) //1次
}
~~~
上述代碼,不管輸入規模n是多少,都執行2次,根據大O推導法則,常數用1來替換,所以上述代碼的時間復雜度 為O(1)
## **3.常見復雜度分析**
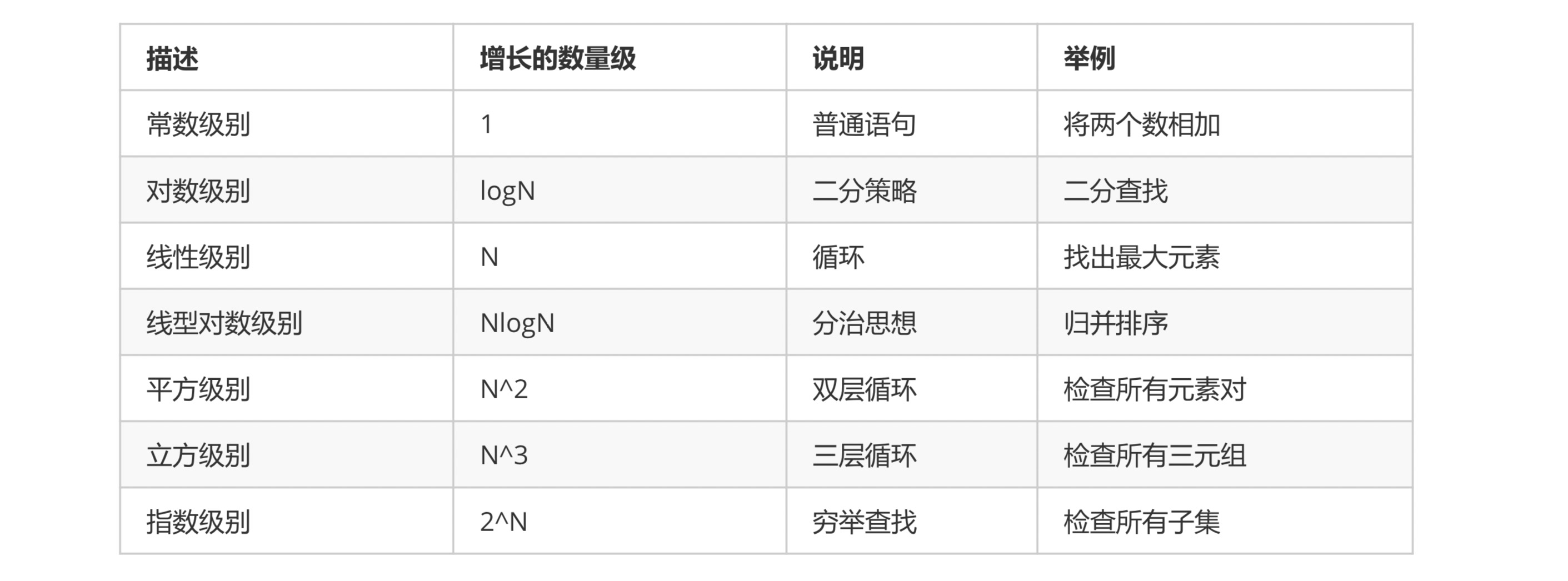
他們的復雜程度從低到高依次為:
O(1)<O(logn)<O(n)<O(nlogn)<O(n^2)<O(n^3)
根據前面的折線圖分析,我們會發現,從平方階開始,隨著輸入規模的增大,時間成本會急劇增大,所以,我們的 算法,盡可能的追求的是O(1),O(logn),O(n),O(nlogn)這幾種時間復雜度,而如果發現算法的時間復雜度為平方階、 立方階或者更復雜的,那我們可以分為這種算法是不可取的,需要優化。
