**本節內容：** [TOC] ## 0.分類算法 | 算法種類 | KNN | 樸素貝葉斯 | 決策樹 | 支持向量機 | 神經網絡 | | --- | --- | --- | --- | --- | --- | | 優點 | 1.簡單易用<br/>2.模型訓練時間短<br/>3.預測效果好<br/>4.對異常值不敏感<br/>5.無數據輸入假定 | 1.接收大量數據訓練和查詢時所具備的高速度，支持增量式訓練<br/>2.對分類器實際學習的解釋相對簡單 | 1.很容易解釋一個受訓模型，算法將最為重要的判斷因素都很好的安排在了靠近樹的根部位置<br/>2.能夠同時處理分類數據和數值數據<br/>3.很容易處理變量之間的相互影響<br/>4.適合小規模數據 | 1.通過將分類輸入轉化為數值輸入，可以令支持向量同時支持分類數據和數值數據<br/>2.適合大規模數據 | 1.能夠處理復雜的非線性函數，并且能發現不同輸入間的依賴關系<br/>2.支持增量式訓練 | | 缺點 | 1.對內存要求較高<br/>2.預測階段可能很慢<br/>3.對不相關的功能和數據規模敏感<br/>4.計算復雜度搞、空間復雜度高 | 1.無法處理基于特征組合所產生的變化結果 | 1.不擅長對數值數據進行預測<br/>2.不支持增量式訓練 | 1.針對每個數據集的最佳核變函數及其相應的參數都是不一樣的，而且每當遇到新的數據集都必須重新確定這些函數及其參數<br/>2.黑盒技術，由于存在高維空間的變換，SVM的分類過程更加難以解釋 | 1.黑盒方法，無法確定推導過程<br/>2.選擇訓練數據的比率與問題相適應的網絡規模方面，沒有明確的規則可以遵循（選擇過高的訓練數據比率有可能導致網絡對噪聲數據產生過度歸納的現象，而選擇過低的訓練比率，則意味著除了已知數據，網絡有可能不會再進一步學習了） | ## 1.KNN算法概述 * KNN是最簡單的分類算法之一，也是最常見的分類算法之一 * KNN算法是<strong style="color:red">有監督學習</strong>中的分類算法 * KNN算法和<strong style="color:red">無監督學習算法K-means</strong>有些相像，但是卻有本質區別 * 使用數據范圍：<strong style="color:red">數值型和標稱型</strong> * 通常K是不大于20的整數 ## 2.KNN算法介紹 KNN全稱為 K Nearest Neighbors，意思是K個最近的鄰居。從名字可知，K的取值是至關重要的。 KNN原理：當預測一個新的值x的時候，根據它距離最近的K個點是什么類別來判斷x屬于哪個類別。 <strong style="color:green">【敲黑板，劃重點】</strong> 如圖，綠色的點是我們要預測的那個點。 假設K=3，那么KNN算法就會找到與它（綠色）距離最近的三個點（為了方便查看，此處用虛線圓圈圈出來），看看哪種類別多一些，比如這個例子中是藍色三角形多一些，所以綠色的點就被歸類為藍色三角形。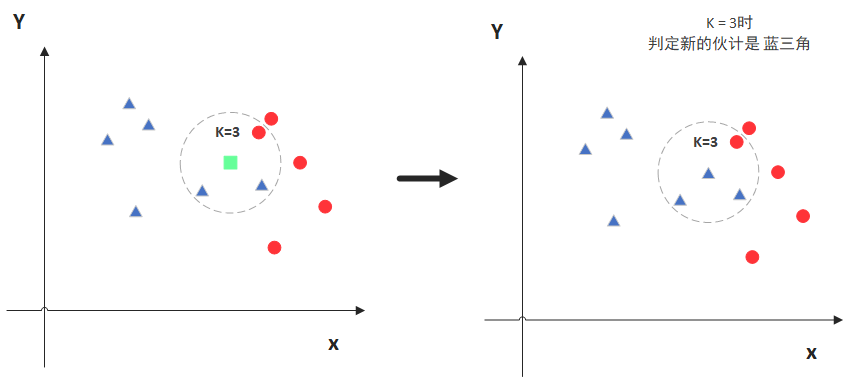  但是，當K=5時，判斷結果就不一樣了。 這次，圈內的紅色圓更多一些，所以綠色的點就被歸類為紅色圓。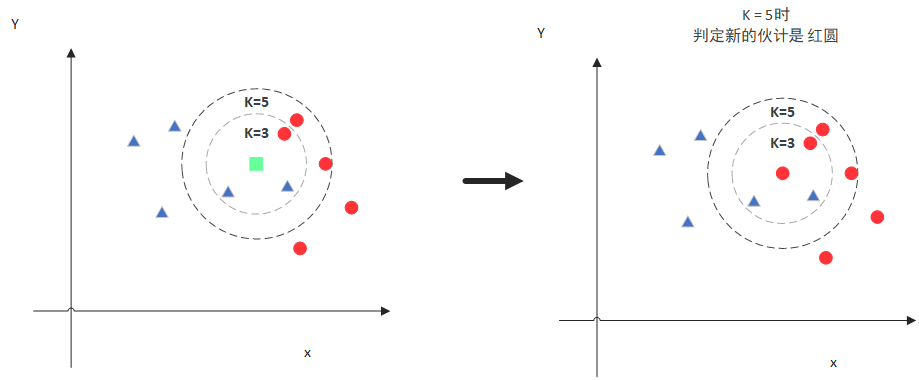  綜上，我們知道，KNN算法中，K的取值是至關重要的。那我們該如何去選取K值，又如何計算點之間的距離呢？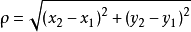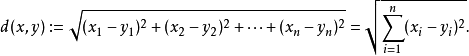 ### 2.1 距離計算 度量空間中點的距離，有幾種常見的度量方式： * 曼哈頓距離計算 * 歐氏距離計算  通常情況下，KNN算法種所使用的是歐式距離：  推演到多維空間，則公式變成： 有兩個元素A和B，每個元素擁有n維屬性， A (x1, x2, x3, ..., xn) B (y1, y2, y3, ..., yn) 則距離公式變為：  此時，我們知道了如何計算元素間距離。 而KNN算法的最簡單粗暴的方式，就是將所有點距離進行計算，然后保存并排序，然后篩選前面K個值看看哪些類別比較多，說白了，也就是個top K的問題。 但是，通常我們也會接觸一些數據結構來輔助獲取top K，比如最大堆（有興趣可以自行百度：[https://blog.csdn.net/cdnight/article/details/11650983](https://blog.csdn.net/cdnight/article/details/11650983)） ### 2.2 K值選擇 K值的選擇是直接影響到我們分類結果的，那么該如何去確定K值呢？ 此時，我們就會采用<strong style="color:red">交叉驗證</strong>（將樣本數據按照一定比例，拆分出訓練集和驗證集，比如6：4比例），然后從選取一個較小的K值開始，不斷增加K的值，然后計算驗證集合的方差，最終找到一個比較合適的K值。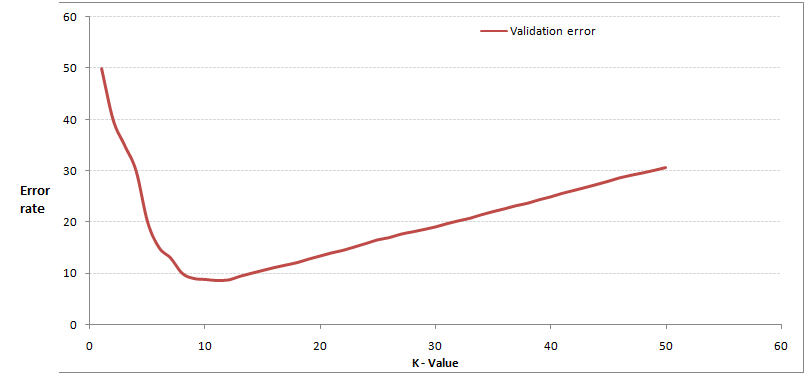 通常，通過交叉驗證計算方差后，你會得到大致類似于下圖：  * 當你增大K的時候，一般錯誤率會先降低，因為有周圍更多的樣本可以借鑒了，分類效果會變好； * 和K-means不一樣，當K值更大的時候，KNN錯誤率會更好 * 比如說你一共就35個樣本，當你K增大到30的時候，KNN基本就沒意義了。 所以選擇K值的時候可以選擇一個較大的臨界K值，當它繼續增大或者減小的時候，錯誤率都會上升。如圖中的K=10 ### 2.3特征歸一化的必要性 首先舉例如下，我用一個人身高(cm)與腳碼（尺碼）大小來作為特征值，類別為男性或者女性。我們現在如果有5個訓練樣本，分布如下： A \[(179,42),男\] B \[(178,43),男\] C \[(165,36)女\] D \[(177,42),男\] E \[(160,35),女\] 通過上述訓練樣本，我們看出問題了嗎？ 很容易看到第一維身高特征是第二維腳碼特征的4倍左右，那么在進行距離度量的時候，<strong style="color:red;">我們就會偏向于第一維特征。</strong>這樣造成倆個特征并不是等價重要的，最終可能會導致距離計算錯誤，從而導致預測錯誤。 <br/> 口說無憑，舉例如下： 現在我來了一個測試樣本 F(167,43)，讓我們來預測他是男性還是女性，我們采取k=3來預測。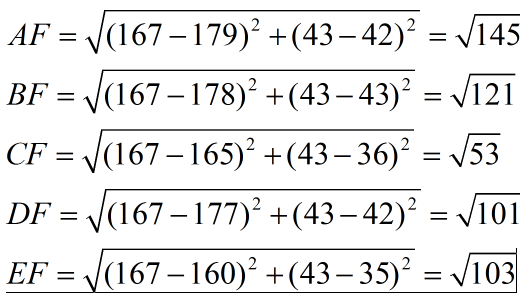 下面我們用歐式距離分別算出F離訓練樣本的歐式距離，然后選取最近的3個，多數類別就是我們最終的結果，計算如下：  由計算可以得到，最近的前三個分別是C,D,E三個樣本，那么由C,E為女性，D為男性，女性多于男性得到我們要預測的結果為**女性**。 <strong style="color:green">Q：</strong>這樣問題就來了，一個女性的腳43碼的可能性，遠遠小于男性腳43碼的可能性，那么為什么算法還是會預測F為女性呢？ <strong style="color:green">A：</strong>那是因為由于各個特征量綱的不同，在這里導致了身高的重要性已經遠遠大于腳碼了，這是不客觀的。所以我們應該讓每個特征都是同等重要的！這也是我們要歸一化的原因！ <strong style="color:red;">歸一化公式如下：</strong>  ## 3.KNN特點 <strong style="color:green">KNN是一種非參、惰性的算法模型。</strong> * 非參 * 并不是說該模型不需要參數，而是意味著這個模型不會對數據做出任何的假設，與之相對應的是線性回歸（我們總會先假設線性回歸是一條直線）。 * 也就是說KNN建立的模型結構是根據數據來決定的，這也比較符合現實的情況，畢竟在現實中的情況往往與理論上的假設是不相符的。 * 惰性 * 邏輯回歸需要先對數據進行大量訓練，最后才會得到一個算法模型。 * KNN算法卻不需要，它沒有明確的訓練數據的過程，或者說這個過程很快。 ## 4.優點 & 缺點？？？ ### 4.1優點： 1. 簡單易用，相比其他算法，KNN算是比較簡潔明了的算法。即使沒有很高的數學基礎也能搞清楚它的原理 2. 模型訓練時間快（KNN算法是惰性的） 3. 預測效果好 4. 對異常值不敏感 ### 4.2缺點： 1. 對內存要求較高，因為該算法存儲了所有訓練數據 2. 預測階段可能很慢 3. 對不相關的功能和數據規模敏感 ## 5.何時選擇KNN算法？？？ 從sklearn給出的圖來解釋：  ## 6.sklearn KNN參數介紹 ` def KNeighborsClassifier(n_neighbors = 5, weights='uniform', algorithm = '', leaf_size = '30', p = 2, metric = 'minkowski', metric_params = None, n_jobs = None ) ` * n_neighbors：KNN的K值 * weights：最普遍的KNN算法無論距離如何，權重都一樣，但有時我們想要特殊化一下數據，比如距離近的點，權重設置更高一些 * 'uniform'：不管遠近權重都一樣，就是最普通的KNN算法形式 * 'distance'：權重和距離成反比，距離預測目標越近擁有越高的權重 * algorithm：在 sklearn 中，要構建 KNN 模型有三種構建方式。暴力法適合數據量較小的方式，否則效率會比較低。如果數據量比較大一般會選擇 KD 樹構建 KNN 模型，而當 KD樹也比較慢的時候，則可以試試球樹來構建 KNN 。依次遞進關系：<strong style="color:red">暴力法 -> KD樹 -> 球樹</strong> * 'brute'：蠻力實現（暴力法），直接計算距離存儲比較的方式 * 'kd_tree'：采用 kd 樹構建 KNN 模型 * 'ball_tree'：采用球樹構建 * 'auto'：默認參數，自動選擇合適的方法構建模型 不過，當數據量較小或者比較稀疏時，無論選擇哪個最后都會使用 'brute' * leaf_size：如果是選擇蠻力實現，則該值可以忽略，當時用KD樹或者球樹，該值是停止建子樹的葉子節點數量的閾值，默認30，但如果數據量增多這個參數需要增大，否則速度過慢不說，還容易過擬合。 * <strong style="color:red">p：和metric結合使用，當metric參數是 "minkowski"的時候，p=1為曼哈頓距離，p=2為歐式距離。默認p=2</strong> * <strong style="color:red">metric：指定距離度量方法，一般都是使用歐式距離。</strong> * 'euclidean'：歐式距離 * 'manhattan'：曼哈頓距離 * 'chebyshev'：切比雪夫距離 * 'minkowski'：閔可夫斯基距離，默認參數 * n_jobs：指定多少個CPU進行運算，默認是-1，即全部都運算。 ## 7.KNN代碼示例 我們直接采用sklearn自帶的鳶尾花數據集進行KNN分類： ### 7.1 交叉驗證確定K值 ```python from sklearn.datasets import load_iris from sklearn.model_selection import cross_val_score import matplotlib.pyplot as plt from sklearn.neighbors import KNeighborsClassifier #讀取鳶尾花數據集 iris = load_iris() x = iris.data y = iris.target k_range = range(1, 31) k_error = [] #循環，取k=1到k=31，查看誤差效果 for k in k_range: knn = KNeighborsClassifier(n_neighbors=k) #cv參數決定數據集劃分比例，這里是按照5:1劃分訓練集和測試集 scores = cross_val_score(knn, x, y, cv=6, scoring='accuracy') k_error.append(1 - scores.mean()) #畫圖，x軸為k值，y值為誤差值 plt.plot(k_range, k_error) plt.xlabel('Value of K for KNN') plt.ylabel('Error') plt.show() ``` 運行結果如下：  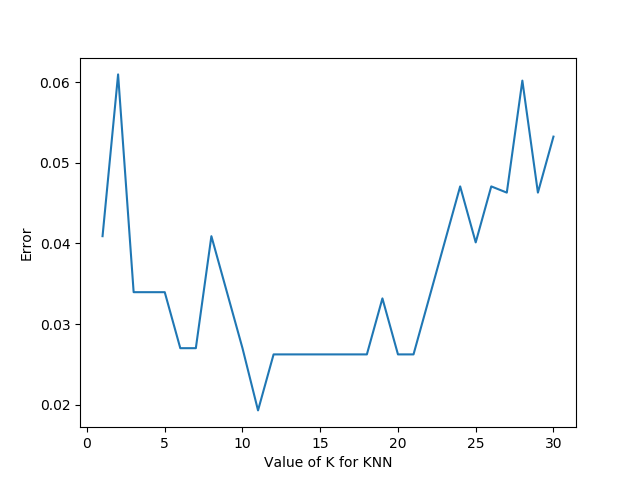從圖中，我們可以明顯看出K值取多少時誤差最小，即K=11。 在實際問題中，如果數據集比較大，那為減少訓練時間，K的取值范圍可以縮小。 ### 7.2 模型預測 ```python import matplotlib.pyplot as plt from numpy import * from matplotlib.colors import ListedColormap from sklearn import neighbors, datasets n_neighbors = 11 # 導入一些要鳶尾花數據 iris = datasets.load_iris() # 我們只采用前兩個feature,方便畫圖在二維平面顯示 x = iris.data[:, :2] y = iris.target # 網格中的步長 h = .02 # 創建彩色的圖 cmap_light = ListedColormap(['#FFAAAA', '#AAFFAA', '#AAAAFF']) cmap_bold = ListedColormap(['#FF0000', '#00FF00', '#0000FF']) #weights是KNN模型中的一個參數，上述參數介紹中有介紹，這里繪制兩種權重參數下KNN的效果圖 for weights in ['uniform', 'distance']: # 創建了一個knn分類器的實例，并擬合數據。 clf = neighbors.KNeighborsClassifier(n_neighbors, weights=weights) clf.fit(x, y) # 繪制決策邊界。為此，我們將為每個分配一個顏色 # 來繪制網格中的點 [x_min, x_max]x[y_min, y_max]. x_min, x_max = x[:, 0].min() - 1, x[:, 0].max() + 1 y_min, y_max = x[:, 1].min() - 1, x[:, 1].max() + 1 xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h)) Z = clf.predict(np.c_[xx.ravel(), yy.ravel()]) # 將結果放入一個彩色圖中 Z = Z.reshape(xx.shape) plt.figure() plt.pcolormesh(xx, yy, Z, cmap=cmap_light) # 繪制訓練點 plt.scatter(x[:, 0], x[:, 1], c=y, cmap=cmap_bold) plt.xlim(xx.min(), xx.max()) plt.ylim(yy.min(), yy.max()) plt.title("3-Class classification (k = %i, weights = '%s')" % (n_neighbors, weights)) plt.show() ``` 結果如圖所示：  ## 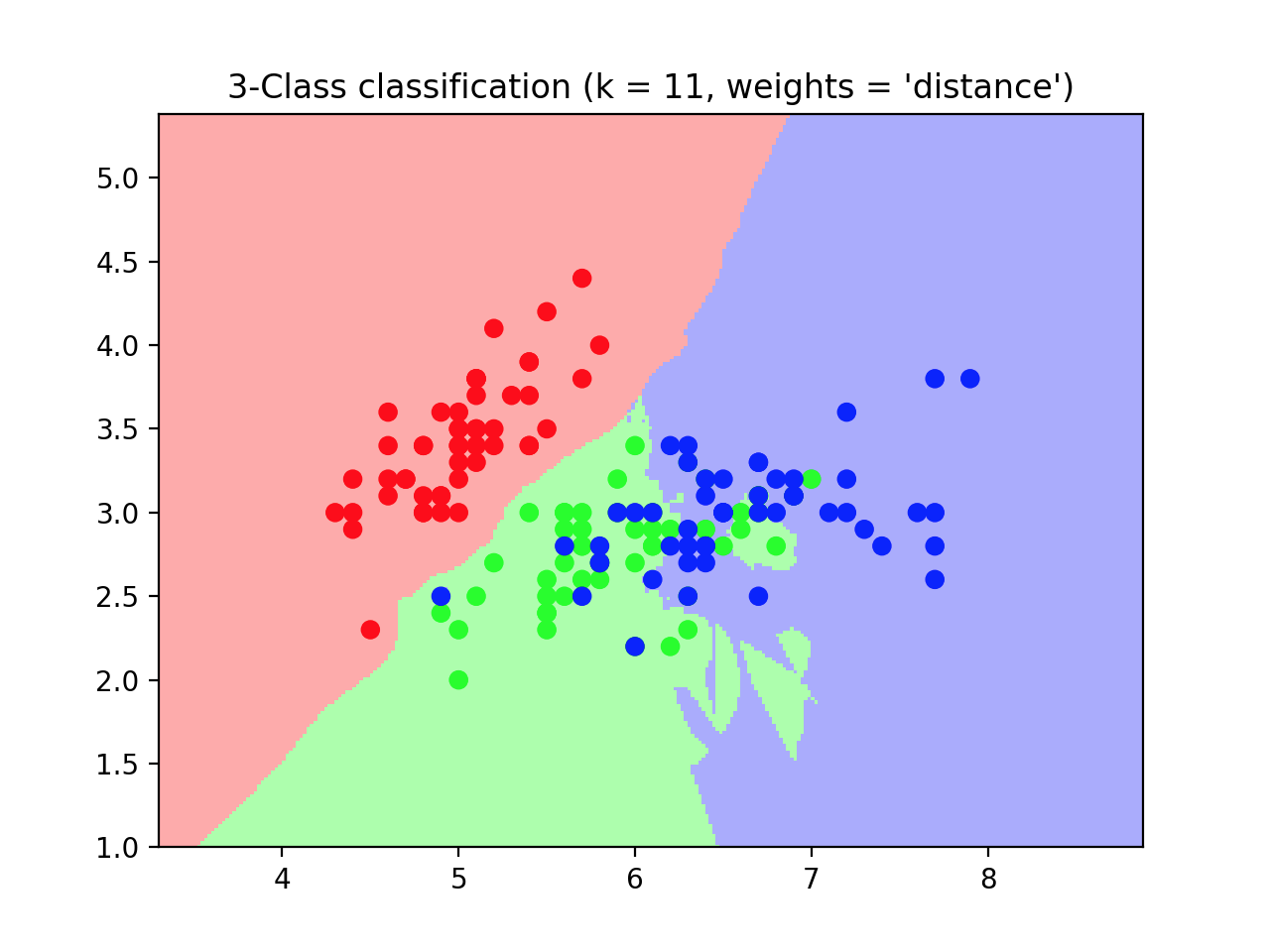8.KNN與K-means異同？？？ * 相同點： * K值都是重點 * 都需要計算平面中點的距離（核心都是通過計算空間中點的距離來實現目的） * 不同點： * 目的不同： * KNN最終目的是分類 * K-means目的是給所有距離相近的點分配一個類別，也就是聚類 <strong style="color:green">【敲黑板，劃重點】</strong> 就是畫一個圈， <strong style="color:red">KNN是讓進來圈子的人變成自己人，</strong> <strong style="color:red">K-means是讓原本在圈內的人歸成一類人。</strong> ## 9.KNN（k-近鄰）算法的一般流程 （1）收集數據：可以使用任何方法。 （2）準備數據：距離計算所需要的的數值，最好是結構化的數據格式。 （3）分析數據：可以使用任何方法。 （4）訓練算法：此步驟不適用k-近鄰算法。 （5）測試算法：計算錯誤率。 （6）使用算法：首先需要輸入樣本數據和結構化的輸出結果，然后運行k-近鄰算法判定輸入數據分別屬于哪個分類，最后應用對計算出的分類執行后續的處理。 ## 參考文獻 * [一文搞懂k近鄰（k-NN）算法](https://zhuanlan.zhihu.com/p/26029567) * [《Machine Learning in Action》 美.Perter Harrington著](http://www.java1234.com/a/javabook/javabase/2018/0618/11382.html?__cf_chl_jschl_tk__=1a9fd8cd05c65e779bf06b71c939ce301af6ba6f-1612414161-0-AS1KkYGWerV7qo3F4MC63eSztes9afmW8sVm1pUj0AA3CXfq5v_PHxGsg6jMvWKM9W4mfnJSCtYBsDQCjdTCBGKfDYhHQLuGBoCBxtLUvJVspQh1LAh0Vt-3fESV6P7AnGZLz1cm4bmFVXSAUPq75GxsqqySPmykRUQ2OEG9Xl3cleceh0Errob0UWroT0YJOQMNV_d7N7EeAvfH8DqesOBHzr_ju1v-skh5JI-kku4QIhpOqxJdgT3PYbnKYjukuJq3axyb7MaX_KaIB3oHk2nRzr8h7cdtUCqQKo7XTx1KSDfYMd60S-jZnK_l363Au8zU9k9N4dXKtNrOiME1no8ElxNb1pzF7G72Gk5ceuze)