**本節內容：** [TOC] ## 引言 貝葉斯原理是英國數學家托馬斯·貝葉斯提出的。貝葉斯是個很神奇的人，他的經歷類似梵高。生前沒有得到重視，死后，他寫的一篇關于歸納推理的論文被朋友翻了出來，并發表了。這一發表不要緊，結果這篇論文的思想直接影響了接下來兩個多世紀的統計學，是科學史上著名的論文之一。<br/> 貝葉斯為了解決一個叫“逆向概率”問題寫了一篇文章，**嘗試解答在沒有太多可靠證據的情況下，怎樣做出更符合數學邏輯的推測。** <strong style="color:red;">什么是“逆向概率”呢？ </strong> 所謂“逆向概率”是相對“正向概率”而言。正向概率的問題很容易理解，比如我們已經知道袋子里面有 N 個球，不是黑球就是白球，其中 M 個是黑球，那么把手伸進去摸一個球，就能知道摸出黑球的概率是多少。**但這種情況往往是上帝視角，即了解了事情的全貌再做判斷。** > 一個袋子里有10個球，其中6個黑球，4個白球；那么隨機抓一個黑球的概率是0.6！ 在現實生活中，我們很難知道事情的全貌。貝葉斯則從實際場景出發，提了一個問題：**如果我們事先不知道袋子里面黑球和白球的比例，而是通過我們摸出來的球的顏色，能判斷出袋子里面黑白球的比例么？** ## 0.分類問題綜述  其中C叫做類別集合，其中每一個元素是一個類別，而 I 叫做項集合（特征集合），其中每一個元素是一個待分類想，f 叫做分類器。 <strong style="color:red;">分類算法的任務就是構造分類器 f </strong> <strong>分類算法的內容是要求給定特征，讓我們得出類別，這也是所有分類問題的關鍵。</strong> ## 1.樸素貝葉斯算法介紹 ### 1.1貝葉斯定理 條件概率是指在事件B發生的情況下，事件A發生的概率。通常記為 P（A | B）  因此，  可得，  <strong style="color:red;">故，貝葉斯公式為：</strong>  這也是條件概率的計算公式。 此外，由全概率公式，可得條件概率的另一種寫法：  其中樣本空間由 A 和 A' 構成，由此求得事件B的概率。 <strong style="color:red;">但是，為了減少計算量，全概率公式在實際編程中可以不使用。</strong><br/> <strong style="color:green;">【敲黑板，劃重點】</strong> 貝葉斯公式中， P（A） &nbsp;&nbsp;&nbsp;&nbsp;稱為“先驗概率”（通過經驗來判斷事情發生的概率），即在B事件發生之前，對A事件概率的一個判斷； P（A | B）稱為“后驗概率”（就是發生結果之后，推測原因的概率），即在B事件發生之后，對A事件概率的重新評估； P（B | A）/ P（B）稱為“可能性函數”，這是一個調整因子，使得預估概率更接近真實概率。 推出， <strong>后驗概率 = 先驗概率 x 調整因子</strong> 這就是貝葉斯推斷的含義：我們先預估一個“先驗概率”，然后加入實驗結果，看這個實驗到底是增強還是削弱了“先驗概率”，由此得到更接近事實的“后驗概率”。 <strong style="color:red;">因此，在分類中，只需要找到可能性最大的那個選項，而不需要知道具體那個類別的概率是多少。</strong> 更重要的是，樸素貝葉斯推斷是在貝葉斯推斷的基礎上，對條件概率分布做了<strong style="color:red;">條件獨立性的假設</strong>。 <strong>因此，如果以自變量之間的獨立（條件特征獨立）性和連續變量的正態性假設為前提，就會導致算法精度在某種程度上受影響。</strong>  ### 1.2樸素貝葉斯 樸素貝葉斯，它是一種簡單但極為強大的預測建模算法。 之所以稱為樸素貝葉斯，是因為它假設每個輸入變量是獨立的。 這個假設在現實生活中根本不滿足，但是這項技術對絕大部分的復雜問題仍然非常有效。<br/> <strong style="color:red;">樸素貝葉斯模型由兩種類型的概率組成：</strong> * 每個類別的概率P（Cj） * 每個屬性的條件概率P（Ai | Cj） 為了訓練樸素貝葉斯模型，我們需要先給出訓練數據，以及這些數據對應的分類。 那么上面這兩個概率，也就是類別概率和條件概率，他們都可以從給出的訓練數據中計算出來，一旦計算出來，概率模型就可以使用貝葉斯原理對新數據進行預測。 <strong style="color:red;">貝葉斯訓練流程</strong>  <strong style="color:red;">那么貝葉斯原理、貝葉斯分類和樸素貝葉斯三者之間是何關系？？？</strong>  * 貝葉斯原理是理論基礎（解決概率論中“逆向概率”的問題），人們在該基礎上，設計出了貝葉斯分類器； * 樸素貝葉斯分類是貝葉斯分類器中的一種，也是最簡單、最常用的分類器； * 樸素貝葉斯之所以樸素是因為<i><strong>它假設屬性是相互獨立的</strong></i>，因此對實際情況有所約束（<strong style="color:green;">如果屬性之間存在關聯，分類準確率會降低。不過好在對于大部分情況下，樸素貝葉斯的分類效果都不錯</strong>）。 ## 2.案例分析 ### 2.1針對不同類型數據，該如何進行樸素貝葉斯的推斷呢？  ### 2.2離散數據案例分析 我們以下面的數據為例，這些是我們之前的經驗所獲得的靜靜打王者情況的數據。然后給出一個新的數據： （課程類型：商業數據分析，心情：不好，朋友都在：在) 請問，此時靜靜會不會打游戲呢？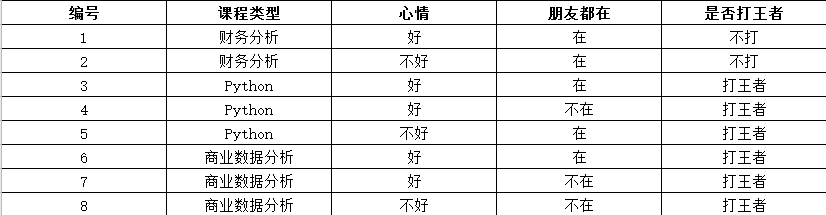  是否打王者就是類別：打王者C1，不打王者C2 屬性條件：課程類型A1，心情A2，朋友都在A3 那么我們想要在A1、A2、A3屬性下，求解Cj的概率，用條件概率表示就是P（Cj | A1A2A3）。 由貝葉斯公式可得：  共有兩種類別，我們只需求得P（C1|A1A2A3）和P（C2|A1A2A3）的概率，然后比較哪個分類的可能性大，就是哪個分類結果，即求P（A1A2A3 | Cj）* P（Cj）的最大值。 <strong style="color:red;">我們假定Ai之間都是相互獨立的，那么：</strong> P（A1A2A3 | Cj）= P（A1 | Cj） * P（A2 | Cj） * P（A3 | Cj） P（A1 | C1） = 3/6 = 1/2 P（A2 | C1） = 2/6 = 1/3 P（A3 | C1） = 3/6 = 1/2 P（A1 | C2） = 0 P（A2 | C2） = 1/2 P（A3 | C2） = 1 P（C1）= 6/8 = 3/4 P（C2）= 2/8 = 1/4 所以， P（A1A2A3 | C1） = 1/12 P（A1A2A3 | C2） = 0 =》 P（A1A2A3 | C1）* P（C1）= 1/16 P（A1A2A3 | C2）* P（C2）= 0 所以 P（C1 | A1A2A3）> P（C2 | A1A2A3），所以應該是C1類別，<strong style="color:red;">即靜靜會打王者（在商業數據分析課，心情不好且朋友都在的時候）的概率大于靜靜不會打王者的概率。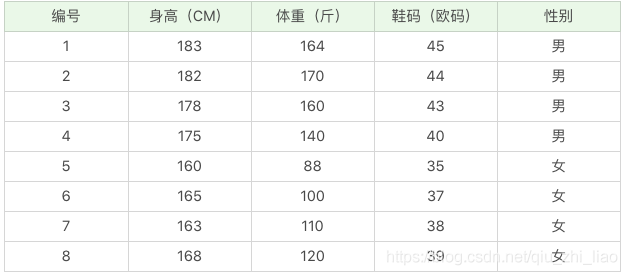</strong> ### 2.3連續數據案例分析  那么如果給你一個新的數據，（身高：180，體重：120，鞋碼 41），請問該人是男是女呢？ <br/> 公式還是上面的公式，這里的困難在于，由于身高、體重、鞋碼都是連續變量，不能采用離散變量的方法計算概率。而且由于樣本太少，所以也無法分成區間計算。怎么辦呢？ <strong style="color:green;">這時，可以假設男性和女性的身高、體重、鞋碼都是正態分布，通過樣本計算出均值和方差，也就是得到正態分布的密度函數。</strong> 有了密度函數，就可以把值代入，算出某一點的密度函數的值。<br/> 比如，**男性的身高**是均值 179.5、標準差為 3.697 的正態分布。（我們選擇不同條件下的樣本，得出的均值，標準差就是條件下的概率分布了。這點稍后計算中體現）<br/> 所以男性的身高為 180 的概率為 0.1069。怎么計算得出的呢? 可以通過 excel 或者 python 工具類<br/> NORMDIST(x,mean,standard\_dev,cumulative) 函數，一共有 4 個參數：  這里我們使用的是 NORMDIST(180,179.5,3.697,0)=0.1069 同理我們可以計算得出男性體重為 120 的概率為 0.000382324 男性鞋碼為 41 號的概率為 0.120304111<br/> 推出， P（C1 | A1A2A3 ） = 4.9169e-6 > P（C2 | A1A2A3） = 2.7244e-9 故，該組數據分類為男性的概率大于分類為女性的概率 ## 3.sklearn實現 scikit-learn中樸素貝葉斯類庫的使用也比較簡單。相對于決策樹，KNN之類的算法，樸素貝葉斯需要關注的參數是比較少的。 在scikit-learn中，一共有3個樸素貝葉斯的分類算法。 * GaussianNB： * 先驗為高斯分布的樸素貝葉斯 * MultionmailNB * 先驗為多項式分布的樸素貝葉斯 * 只有3個參數： * alpha（拉普拉斯平滑） * fit_prior（表示是否要考慮先驗概率） * class_prior：可選參數 * MultionmailNB的一個重要的功能是partial_fit方法，這個方法一般用在訓練接數據量非常大，一次不能全部載入內存的時候。這是我們可以把訓練集分成若干等份，重復調用partial_fit來一步步的學習訓練集，非常方便。 * BernoulliNB * 先驗為伯努利分布的樸素貝葉斯 更多scikit-learn中樸素貝葉斯相關可以查看官方文檔：[sklearn.naive_bayes.MultionmailNB](https://scikit-learn.org/dev/modules/generated/sklearn.naive_bayes.MultinomialNB.html) ## 4.項目實踐 - 基于美團評論的文本情感分析 先貼上源碼：[comment-model-analysis](https://github.com/buildupchao/comment-model-analysis)  ### 4.1數據清洗 ```python import os import random import jieba from sklearn.model_selection import train_test_split # from sklearn.feature_extraction.text import TfidfVectorizer from sklearn.feature_extraction.text import CountVectorizer """ 讀取源數據 """ def get_txt_data(txt_file): most_words = [] try: file = open(txt_file, 'r', encoding='utf-8') for line in file.readlines(): current_line = line.strip().split("\t") most_words.append(current_line) file.close() except: try: file = open(txt_file, 'r', encoding='gb2312') for line in file.readlines(): current_line = line.strip().split("\t") most_words.append(current_line) file.close() except: try: file = open(txt_file, 'r', encoding='gbk') for line in file.readlines(): current_line = line.strip().split("\t") most_words.append(current_line) file.close() except: '' return most_words """ 獲取停用詞 """ def load_and_merge_stopwords(): stopwords_set = set() # load stopwords into set collection so as to distinct for root, dirs, filename_list in os.walk(r'../data/stop_words'): for filename in filename_list: file = open(root + '/' + filename, 'r') for line in file: if len(line.strip()): stopwords_set.add(line.strip()) file.close() print("加載停用詞已完成，停用詞共 %d 個" % len(stopwords_set)) return list(stopwords_set) def context_cut(stopwords, sentence): cut_words_str = "" cut_words_list = [] cut_words = list(jieba.cut(sentence)) for word in cut_words: if word in stopwords: continue else: cut_words_list.append(word) cut_words_str = ','.join(cut_words_list) return cut_words_str, cut_words_list def do_data_etl(using_test_dataset=False): # 1.提取停用詞 stopwords = load_and_merge_stopwords() # 2.讀取數據集，進行分詞且過濾掉停用詞 words = [] word_list = [] neg_doc = [] if using_test_dataset: neg_doc = get_txt_data('../data/neg_head.txt') else: neg_doc = get_txt_data('../data/neg.txt') for line_info in neg_doc: cut_words_str, cut_words_list = context_cut(stopwords, line_info[0]) word_list.append((cut_words_str, -1)) words.append(cut_words_list) neg_lena = len(word_list) print("加載消極情緒數據集，共 %d 條" % neg_lena) pos_doc = [] if using_test_dataset: pos_doc = get_txt_data('../data/pos_head.txt') else: pos_doc = get_txt_data('../data/pos.txt') for line_info in pos_doc: cut_words_str, cut_words_list = context_cut(stopwords, line_info[0]) word_list.append((cut_words_str, 1)) words.append(cut_words_list) print("加載積極情緒數據集，共 %d 條" % (len(word_list) - neg_lena)) random.shuffle(word_list) print("加載數據集完成，數據共 %d 條" % (len(word_list))) x, y = zip(*word_list) x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=42, test_size = 0.25) print("數據分割已完成，訓練數據集共 %d 條，測試數據集共 %d 條" % (len(x_train), len(x_test))) # 3.提取特征向量 # vectorizer = TfidfVectorizer(analyzer='word', ngram_range=(1, 4), max_features=500) vectorizer = CountVectorizer() return x_train, x_test, y_train, y_test, vectorizer ``` ### 4.2模型訓練及使用 ```python from sklearn.naive_bayes import MultinomialNB from data_etl import etl from sklearn.pipeline import make_pipeline from result_display import display ''' 使用CountVectorizer進行特征提取，使用MultinomialNB分類訓練 ''' X_train, X_test, y_train, y_test, vectorizer = etl.do_data_etl() classifier = MultinomialNB() pipeline = make_pipeline(vectorizer, classifier) history = pipeline.fit(X_train, y_train) y_predict = pipeline.predict(X_test) display.display_report(y_test, y_predict) ``` 結果展示：   ## 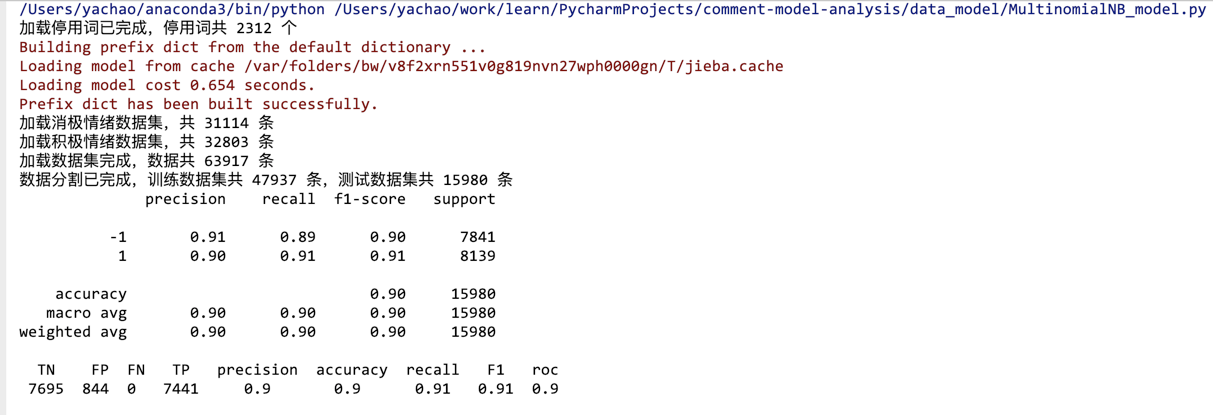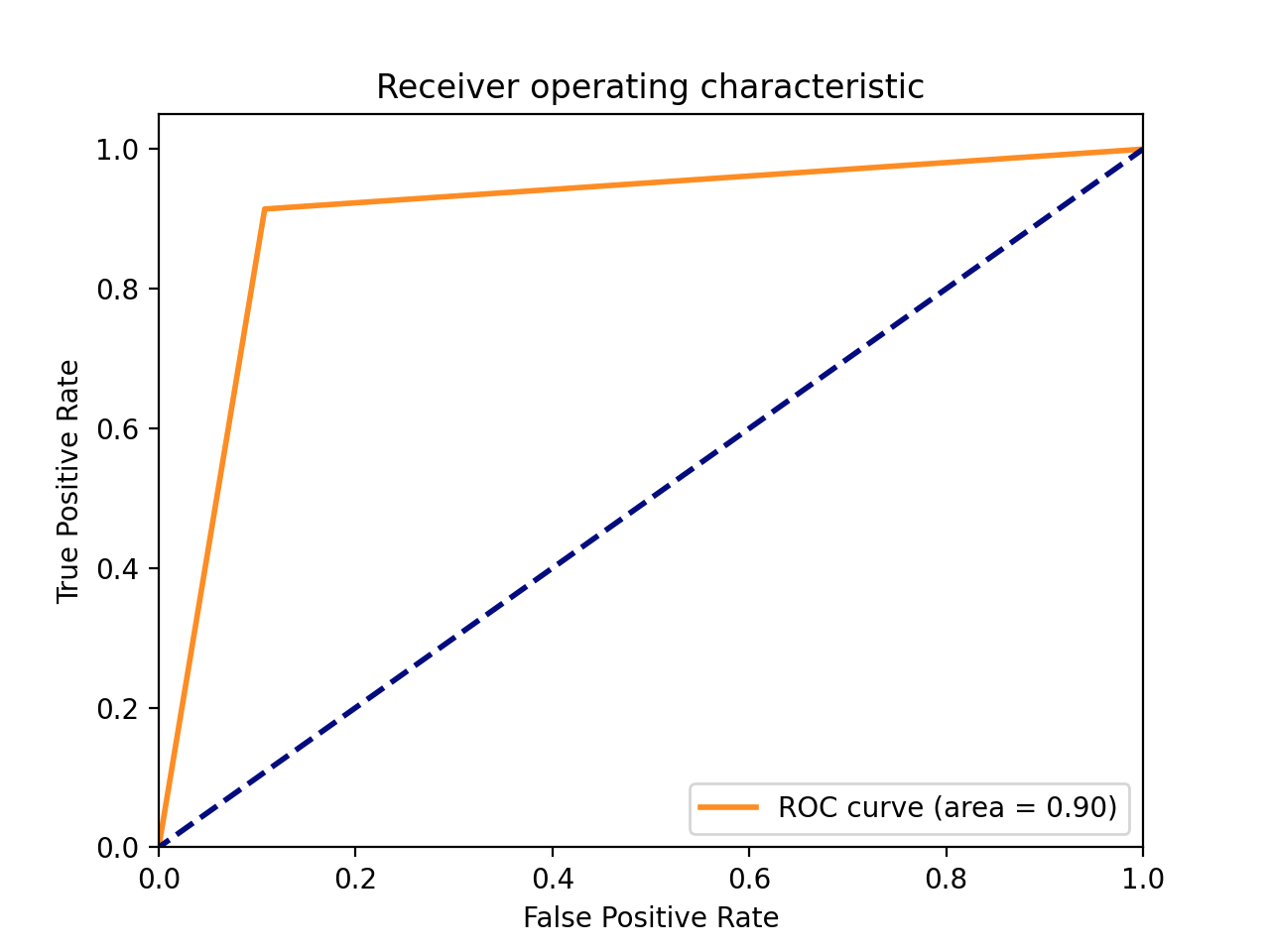5.總結 ### 5.1概率依據 * 先驗概率： * 憑借經驗得出的概率 * 條件概率： * 知道原因，推測結果的概率 * 后驗概率： * 知道結果推測原因發生的概率  ### 5.2貝葉斯適用場景及各階段分布 <strong style="color:green;">樸素貝葉斯分類常用于文本分類，尤其是對于英文等語言來說，分類效果很好。</strong>它常用于垃圾文本過濾、情感預測、推薦系統等。 * 準備階段<strong style="color:red;">（打標簽、分割數據集）</strong>： * 確定特征屬性，明確預測值是什么。 * 數據清洗（格式轉換等）、打標簽（數據分類） * 分割數據（訓練集、測試集/驗證集） * 該階段對整個過程將有重要影響，分類器的質量很大程度上由特征屬性、特征屬性劃分及訓練樣本質量決定。 * 訓練階段<strong style="color:red;">（模型訓練與驗證）</strong>： * 生成分類器，主要工作是計算每個類別在訓練樣本中的出現頻率及每個特征屬性劃分對每個類別的條件概率。 * 輸入：特征屬性和訓練樣本 * 輸出：分類器 * 應用階段<strong style="color:red;">（模型上線應用）</strong>： * 使用分類器對新數據進行分類 * 輸入：分類器和新數據 * 輸出：新數據的分類結果 ### 5.3貝葉斯算法優缺點？？？ * 優點： * 有穩定的分類效率（發源于古典數學理論） * 對小規模的數據表現很好，能處理多分類任務，適合增量式訓練，尤其是數據量超出內存時，我們可以一批批的去<strong style="color:green;">增量訓練</strong> *<strong style="color:green;"> 對缺失數據不太敏感，算法也比較簡單，常用于文本分類</strong> * 缺點： * 樸素貝葉斯模型在給定輸出類別的情況下，假設屬性之間相互獨立 * 這個假設在實際應用中往往是不成立的，在屬性個數比較多或者屬性之間相關性較大時，分類效果不好。 * 在屬性相關性較小時，樸素貝葉斯性能最為良好。 * 對于這一點，有<strong style="color:green;">半樸素貝葉斯之類的算法</strong>通過考慮部分相關性適度改進。 * 需要知道先驗概率，且先驗概率很多時候取決于假設，假設的模型可以有很多種，因此在某些時候會由于假設的先驗模型的原因導致預測效果不佳。 * 由于我們是通過先驗和數據來決定后驗的概率，從而決定分類，所以分類決策存在一定的錯誤率。 * <strong style="color:green;">對輸入數據的表現形式很敏感。</strong> ## 6.課后思考題 如果你的男/女朋友，在你的微信里面發現你和別的女/男人的曖昧聊天記錄，于是他/她開始思考了3個概率問題，那么以下3個問題分別屬于哪種概率呢？？？（答案選項從“先驗概率、后驗概率、條件概率”中選擇）： （1）你在沒有任何征兆的情況下，出軌的概率； （2）在你的微信里面發現了曖昧聊天記錄，認為你出軌的概率； （3）如果你出軌了，那么你的微信里面有曖昧聊天記錄的概率。<br/> <strong style="color:green;">答案就在5.1部分哦（總結的順序就是答案的順序）！</strong> ## 參考資料 * [算法雜貨鋪——分類算法之樸素貝葉斯分類(Naive Bayesian classification)](https://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html) * [樸素貝葉斯分類實例-單詞糾正問題](https://zhuanlan.zhihu.com/p/26653332) * [樸素貝葉斯分類器的應用](http://www.ruanyifeng.com/blog/2013/12/naive_bayes_classifier.html) * [樸素貝葉斯算法（Naive Bayes）](https://www.jianshu.com/p/5953923f43f0) * [《Machine Learning in Action》 美.Perter Harrington著](http://www.java1234.com/a/javabook/javabase/2018/0618/11382.html?__cf_chl_jschl_tk__=1a9fd8cd05c65e779bf06b71c939ce301af6ba6f-1612414161-0-AS1KkYGWerV7qo3F4MC63eSztes9afmW8sVm1pUj0AA3CXfq5v_PHxGsg6jMvWKM9W4mfnJSCtYBsDQCjdTCBGKfDYhHQLuGBoCBxtLUvJVspQh1LAh0Vt-3fESV6P7AnGZLz1cm4bmFVXSAUPq75GxsqqySPmykRUQ2OEG9Xl3cleceh0Errob0UWroT0YJOQMNV_d7N7EeAvfH8DqesOBHzr_ju1v-skh5JI-kku4QIhpOqxJdgT3PYbnKYjukuJq3axyb7MaX_KaIB3oHk2nRzr8h7cdtUCqQKo7XTx1KSDfYMd60S-jZnK_l363Au8zU9k9N4dXKtNrOiME1no8ElxNb1pzF7G72Gk5ceuze) * [sklearn.naive_bayes.MultionmailNB](https://scikit-learn.org/dev/modules/generated/sklearn.naive_bayes.MultinomialNB.html) * [基于機器學習的文本情感分類](https://blog.csdn.net/qq_24206673/article/details/108004099)