* [ ] 在網絡傳播理論與實踐課上,呂欣老師提到了 “媒體黃金時間的重新定義”。交通廣播的黃金時間是 6:00 – 7:00 和 17:30 – 18:30 的早晚交通高峰,電視的黃金時間是 19:00 – 21:00,到了移動互聯網時代,手機和我們互相成為延伸,不再像廣播、電視那樣那么受限于使用的場景。那么這個時代的黃金時間是什么?
* [ ] 大家不妨思考一下這個問題:
**你認為什么時候發朋友圈最合適?**
有人說,晚飯后發朋友圈最合適,因為那個時候大部分人都會閑下來刷朋友圈;也有人說,晚上發朋友圈的人太多了,自己發的內容太容易被淹沒,反而更難取得關注;還有人說,早起發朋友圈更好、正午發朋友圈更好,因為大家有起床后工作前或是午飯后刷朋友圈的習慣,而且那時朋友圈更新的頻率比較小……
* [ ] 以上都是大家對朋友圈發布的基于經驗的思考,經驗會不會出錯呢?我想研究一下。
首先,我們發朋友圈最期待的就是兩個反饋:點贊和評論,因為它們是由我們所發布的內容轉化而來的,所以我們稱之為 “**轉化量**”。來看看我朋友圈一天中點贊量和評論量在 24 小時時間上的分布,其中圖中的每一個點代表一條朋友圈,縱坐標是其收獲的點贊量 / 評論量,橫坐標是朋友圈發布的時間。
:-: 朋友圈點贊數與時間散點圖

:-: 朋友圈評論數與時間散點圖
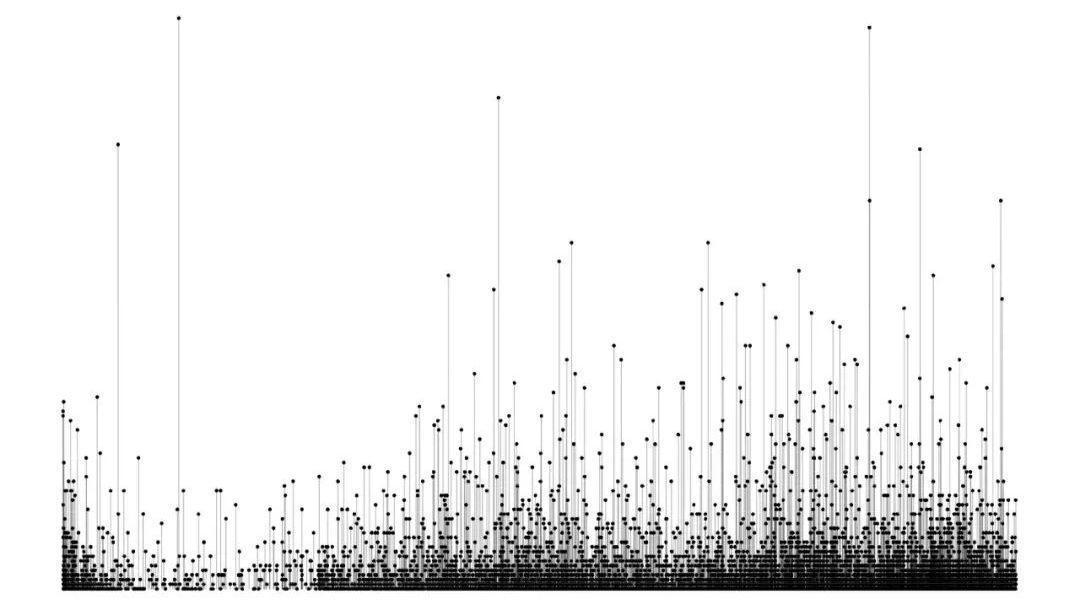
看到這里,很多人就想下結論了,顯然朋友圈晚上發最合適嘛,晚上的點又高又密。真的是這樣嗎?這其中有許多的問題。
首先是樣本,圖中的 7418 個點代表我獲取我的朋友圈的 7418 條數據,局限性很大,不能代表所有人朋友圈的發布情況。其次,點的密度大只能說明該時段朋友圈的發布量大,這沒什么。還有,晚上點贊量高的朋友圈多,但點贊量低的朋友圈也多,**點贊量的期望**真的會高于其他時段嗎?
拋開樣本的局限性不說,我們先看一看這些朋友圈都是在什么時候發的:
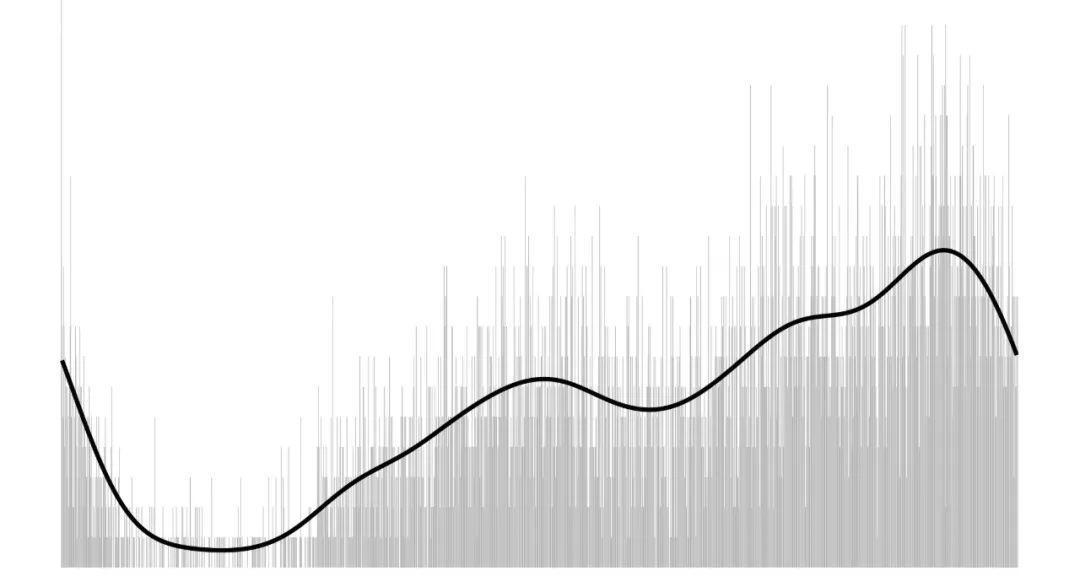
:-: 朋友圈發布時間直方圖
工作日和周末各時段的平均發布量對比圖:
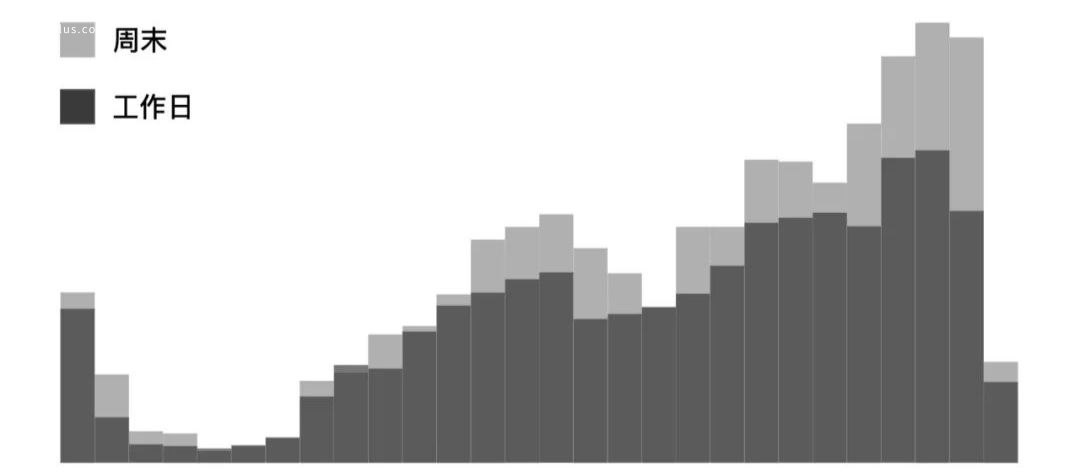
可以看出,我的朋友喜歡在正午、傍晚、和晚間發布朋友圈,在每晚 21:00 – 23:00 達到全日的最高峰。同時,周末的高峰比工作日更高。
這就是為什么有人會覺得晚上發朋友圈會被 “淹沒” 了。
可是,發朋友圈的人多,看朋友圈的人也會多啊!我把一天拆成 48 個時段,統計每個時段朋友圈的數量、點贊總量、評論總量,繪制成如下散點圖。
:-: 各時間段點贊量(黑)、評論量(灰)與發布量的散點圖與擬合直線
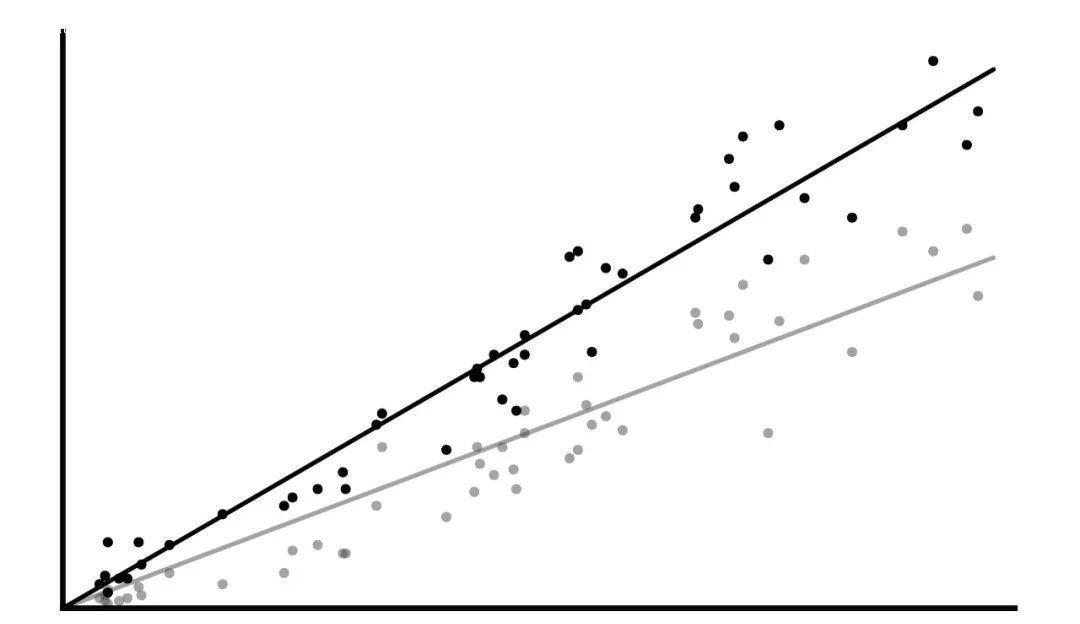
其中,每一個點代表一個時段,橫坐標是其間朋友圈的數量,縱坐標是其點贊總量(黑)/ 評論總量(灰)。再進行一波線性擬合,發現……無論什么時候發朋友圈,獲得點贊、評論數量的期望幾乎是一樣的,一樣的!
這可真是太尷尬了。
這個時候老師發來了一條公式:**選擇或然率公式**。

將其投影在微信朋友圈上,我也得出了一條類似的公式:(微信朋友圈)轉化量公式。

進行簡單的轉換,可以得出:
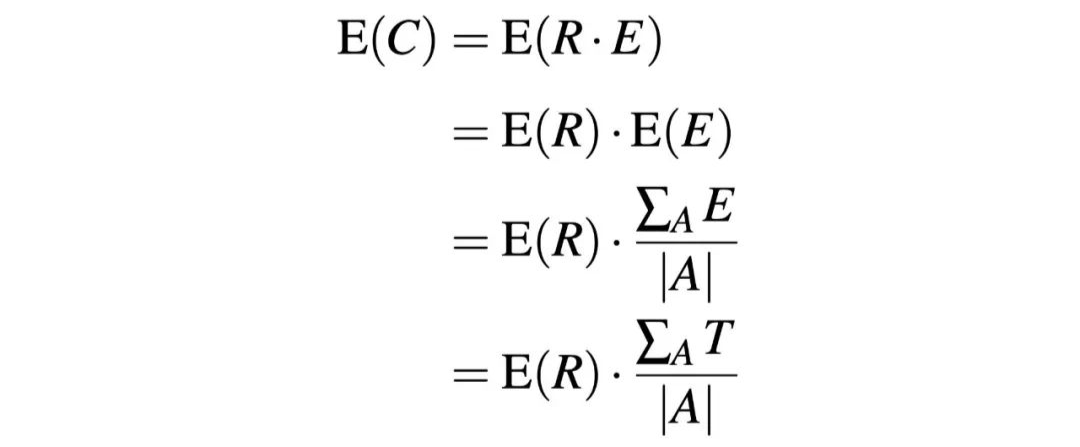
也就是:

所以,轉化量期望恒定的源頭就在于:我們發朋友圈的時間和瀏覽朋友圈的時間分布幾乎是一致的。
等等,回到剛才的問題,期望一樣又能怎樣呢?**期望恒定了,我們獲得更大轉化量的機會也恒定了嗎?**
這時,我們來關注一個新的指標:**注意熵**。
微信朋友圈的發布、瀏覽、點贊、評論都是**符號互動**的重要組成,它形成了比以往更多的人與人之間的**強弱互惠性服務關系**。這些互動拓展了個體維持關系的能力,同時也擠壓了用戶的時間,占用了用戶的注意力。
假設我們的注意在各條朋友圈之間的分配是完全隨機的,那么各條朋友圈獲得的曝光機會也就是相等的。但事實上,我們的注意力會集中在某幾個位置而忽視其余位置,我們怎樣去描述**注意的集中或分散程度**?
基于香農的信息熵理論,用戶朋友圈的注意熵可以反應用戶**注意的不確定性**。
熵被用來衡量一個隨機變量出現的期望值,計算方法是:
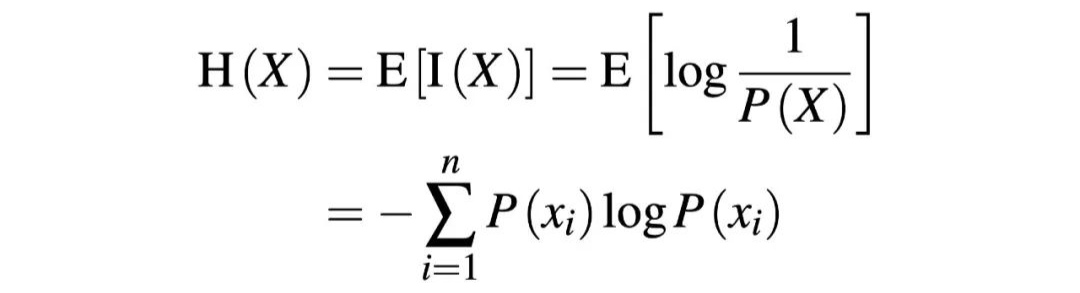
我將點贊以及評論數據作為計算注意熵的來源,探究用戶注意的分散度。對于一份點贊樣本 C,P(ci) =ci/∑C,即某條朋友圈的點贊數可反應用戶注意停留在該內容上的概率。
同樣把一天分為 48 個時段,對每個時段的所有朋友圈計算注意熵,可以得到總注意熵的趨勢圖:
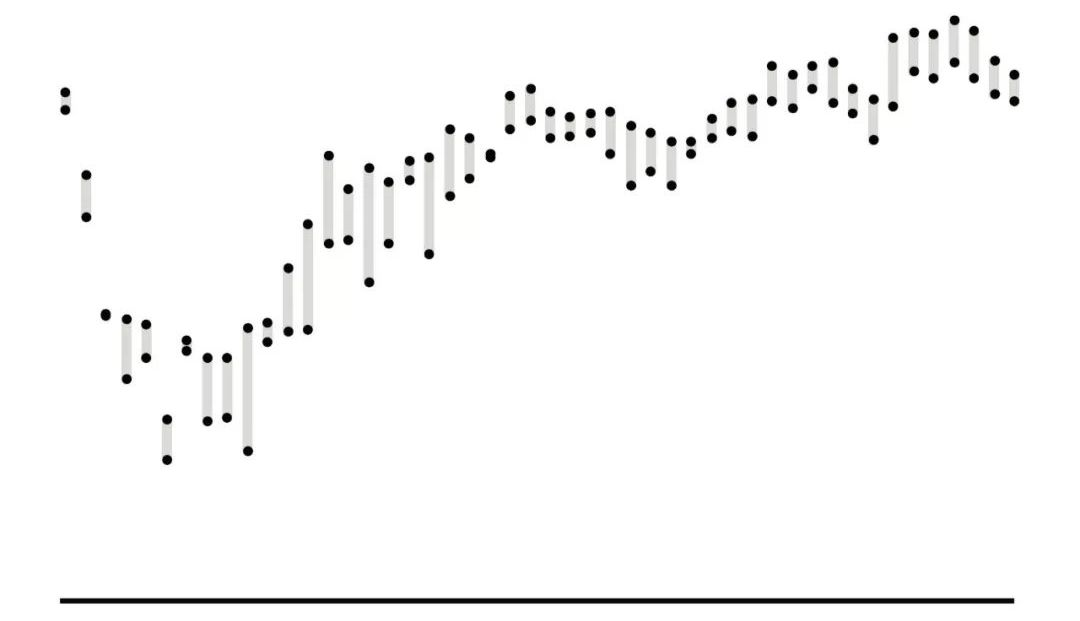
:-: 各時間段的總注意熵
如果對每個時段取定量的朋友圈樣本,可以繪制各時段確定樣本數注意熵的趨勢圖:

:-: 各時間段確定樣本數的注意熵
由圖可知,在一個確定時間段內,用戶的注意的隨機性會因內容的增多而變強,而在一個確定數量的樣本中,用戶注意的隨機性幾乎恒定。
這就說明,用戶瀏覽內容時,注意力出現的概率是恒定的,即用戶出現對某條朋友圈關注度提升的概率是恒定的,但是用戶的注意總量會被有限時間的內容數量所稀釋,信息量越大,用戶隨時間分配注意的隨機性越強。
太玄學了。
緊接著,我的神仙老師又發來了一本書——**巴拉巴西的《鏈接》**,讀完之后,我發現其中**無尺度網絡**的**冪律分布**同樣適用于微信朋友圈。
首先,我們把我朋友圈的每一個用戶視作一個**節點**,每一個次點贊都形成兩個節點之間的**有向邊**,這樣一來,一個**有向圖**就形成了:

一個相同階數和邊數的**隨機圖**:

統計兩個圖中各個節點的**度**(節點連接的邊數),可以發現,朋友圈的圖的度的分布是**冪律分布**,而隨機圖的分布是**二項式分布**。對于冪律分布來說,研究其**度的期望**的意義不很大。
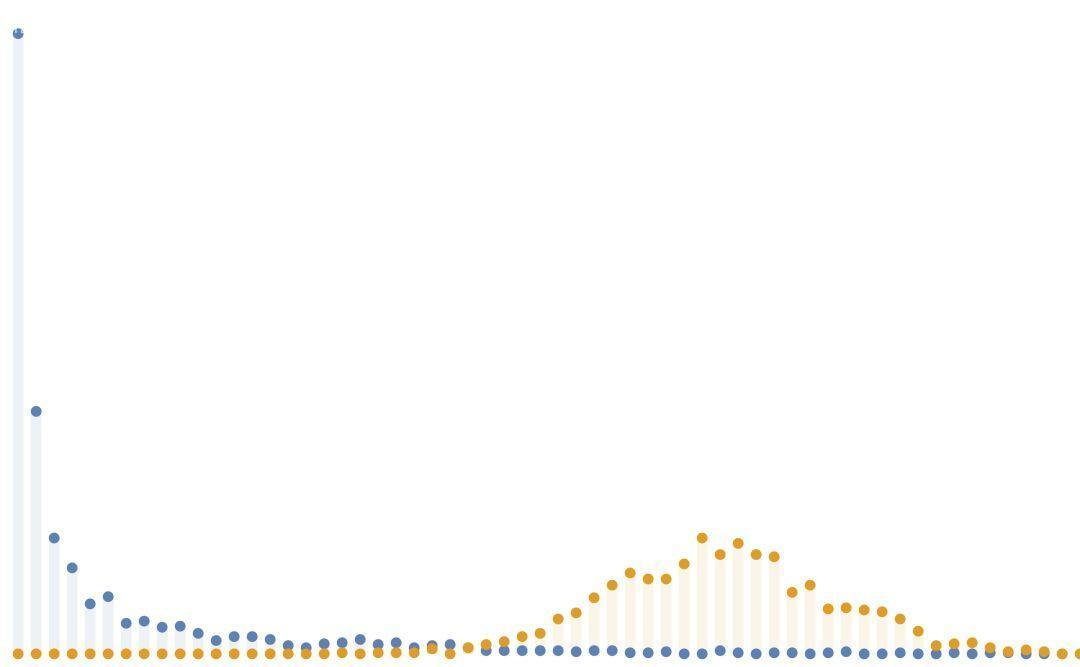
:-: 二圖度分布對比圖
平均沒有意義,多少不是關鍵。
綜上所述,如果朋友圈的質量足夠高,那么我們可以一直維持在自己朋友圈這個冪律分布的頂端節點——那個擁有連接數最多的節點,這個時候,朋友圈轉化率的期望值沒有意義——它幾乎是恒定的,朋友圈發布的數量不是關鍵——大部分朋友圈會被 “淹沒”,起決定作用的就是我們獲得的曝光量。所以,質量足夠高,什么時候 “人多” 什么時候發,這,就是互聯網時代的 “黃金時間”。
用《鏈接》里的另一句話作為此次小思考的收尾:**節點永遠在為鏈接而競爭**。
One more thing……

:-: 根據點贊關系繪制的社區圖,可以非常精準的分類我的各個好友群體
*****
非常感謝呂欣老師、沈浩老師、孫國玉老師、張輝老師的悉心教導!
