# 10\. 分析句子的意思
我們已經看到利用計算機的能力來處理大規模文本是多么有用。現在我們已經有了分析器和基于特征的語法,我們能否做一些類似分析句子的意思這樣有用的事情?本章的目的是要回答下列問題:
1. 我們如何能表示自然語言的意思,使計算機能夠處理這些表示?
2. 我們怎樣才能將意思表示與無限的句子集合關聯?
3. 我們怎樣才能使用程序來連接句子的意思表示到知識的存儲?
一路上,我們將學習一些邏輯語義領域的形式化技術,看看如何用它們來查詢存儲了世間真知的數據庫。
## 1 自然語言理解
## 1.1 查詢數據庫
假設有一個程序,讓我們輸入一個自然語言問題,返回給我們正確的答案:
```py
>>> nltk.data.show_cfg('grammars/book_grammars/sql0.fcfg')
% start S
S[SEM=(?np + WHERE + ?vp)] -> NP[SEM=?np] VP[SEM=?vp]
VP[SEM=(?v + ?pp)] -> IV[SEM=?v] PP[SEM=?pp]
VP[SEM=(?v + ?ap)] -> IV[SEM=?v] AP[SEM=?ap]
NP[SEM=(?det + ?n)] -> Det[SEM=?det] N[SEM=?n]
PP[SEM=(?p + ?np)] -> P[SEM=?p] NP[SEM=?np]
AP[SEM=?pp] -> A[SEM=?a] PP[SEM=?pp]
NP[SEM='Country="greece"'] -> 'Greece'
NP[SEM='Country="china"'] -> 'China'
Det[SEM='SELECT'] -> 'Which' | 'What'
N[SEM='City FROM city_table'] -> 'cities'
IV[SEM=''] -> 'are'
A[SEM=''] -> 'located'
P[SEM=''] -> 'in'
```
這使我們能夠分析 SQL 查詢:
```py
>>> from nltk import load_parser
>>> cp = load_parser('grammars/book_grammars/sql0.fcfg')
>>> query = 'What cities are located in China'
>>> trees = list(cp.parse(query.split()))
>>> answer = trees[0].label()['SEM']
>>> answer = [s for s in answer if s]
>>> q = ' '.join(answer)
>>> print(q)
SELECT City FROM city_table WHERE Country="china"
```
注意
**輪到你來:**設置跟蹤為最大,運行分析器,即`cp = load_parser('grammars/book_grammars/sql0.fcfg', trace=3)`,研究當邊被完整的加入到圖表中時,如何建立`sem`的值。
最后,我們在數據庫`city.db`上執行查詢,檢索出一些結果:
```py
>>> from nltk.sem import chat80
>>> rows = chat80.sql_query('corpora/city_database/city.db', q)
>>> for r in rows: print(r[0], end=" ") ![[1]](https://img.kancloud.cn/97/aa/97aa34f1d446f0c464068d0711295a9a_15x15.jpg)
canton chungking dairen harbin kowloon mukden peking shanghai sian tientsin
```
由于每行`r`是一個單元素的元組,我們輸出元組的成員,而不是元組本身[![[1]](https://img.kancloud.cn/97/aa/97aa34f1d446f0c464068d0711295a9a_15x15.jpg)](./ch10.html#tuple-val)。
總結一下,我們已經定義了一個任務:計算機對自然語言查詢做出反應,返回有用的數據。我們通過將英語的一個小的子集翻譯成 SQL 來實現這個任務們可以說,我們的 NLTK 代碼已經“理解”SQL,只要 Python 能夠對數據庫執行 SQL 查詢,通過擴展,它也“理解”如 What cities are located in China 這樣的查詢。這相當于自然語言理解的例子能夠從荷蘭語翻譯成英語。假設你是一個英語為母語的人,已經開始學習荷蘭語。你的老師問你是否理解[(3)](./ch10.html#ex-sem1)的意思:
```py
>>> nltk.boolean_ops()
negation -
conjunction &
disjunction |
implication ->
equivalence <->
```
從命題符號和布爾運算符,我們可以建立命題邏輯的規范公式(或簡稱公式)的無限集合。首先,每個命題字母是一個公式。然后,如果φ是一個公式,那么`-`φ也是一個公式。如果φ和ψ是公式,那么`(`φ `&` ψ`)` `(`φ `|` ψ`)` `(`φ `->` ψ`)` `(`φ `<->` ψ`)`也是公式。
[2.1](./ch10.html#tab-boolean-tcs)指定了包含這些運算符的公式為真的條件。和以前一樣,我們使用φ和ψ作為句子中的變量,iff 作為 if and only if(當且僅當)的縮寫。
表 2.1:
命題邏輯的布爾運算符的真值條件。
```py
>>> read_expr = nltk.sem.Expression.fromstring
>>> read_expr('-(P & Q)')
<NegatedExpression -(P & Q)>
>>> read_expr('P & Q')
<AndExpression (P & Q)>
>>> read_expr('P | (R -> Q)')
<OrExpression (P | (R -> Q))>
>>> read_expr('P <-> -- P')
<IffExpression (P <-> --P)>
```
從計算的角度來看,邏輯給了我們進行推理的一個重要工具。假設你表達 Freedonia is not to the north of Sylvania,而你給出理由 Sylvania is to the north of Freedonia。在這種情況下,你已經給出了一個論證。句子 Sylvania is to the north of Freedonia 是論證的假設,而 Freedonia is not to the north of Sylvania 是結論。從假設一步一步推到結論,被稱為推理。通俗地說,就是我們以在結論前面寫 therefore 這樣的格式寫一個論證。
```py
>>> lp = nltk.sem.Expression.fromstring
>>> SnF = read_expr('SnF')
>>> NotFnS = read_expr('-FnS')
>>> R = read_expr('SnF -> -FnS')
>>> prover = nltk.Prover9()
>>> prover.prove(NotFnS, [SnF, R])
True
```
這里有另一種方式可以看到結論如何得出。`SnF -> -FnS`在語義上等價于`-SnF | -FnS`,其中 "`|`"是對應于 or 的二元運算符。在一般情況下,φ`|`ψ在條件 _s_ 中為真,要么φ在 _s_ 中為真,要么ψ在 _s_ 中為真。現在,假設`SnF`和`-SnF | -FnS`都在 _s_ 中為真。如果`SnF`為真,那么`-SnF`不可能也為真;經典邏輯的一個基本假設是:一個句子在一種情況下不能同時為真和為假。因此,`-FnS`必須為真。
回想一下,我們解釋相對于一個模型的一種邏輯語言的句子,它們是這個世界的一個非常簡化的版本。一個命題邏輯的模型需要為每個可能的公式分配值`True`或`False`。我們一步步的來做這個:首先,為每個命題符號分配一個值,然后確定布爾運算符的含義(即[2.1](./ch10.html#tab-boolean-tcs))和運用它們到這些公式的組件的值,來計算復雜的公式的值。`估值`是從邏輯的基本符號映射到它們的值。下面是一個例子:
```py
>>> val = nltk.Valuation([('P', True), ('Q', True), ('R', False)])
```
我們使用一個配對的鏈表初始化一個`估值`,每個配對由一個語義符號和一個語義值組成。所產生的對象基本上只是一個字典,映射邏輯符號(作為字符串處理)為適當的值。
```py
>>> val['P']
True
```
正如我們稍后將看到的,我們的模型需要稍微更加復雜些,以便處理將在下一節中討論的更復雜的邏輯形式;暫時的,在下面的聲明中先忽略參數`dom`和`g`。
```py
>>> dom = set()
>>> g = nltk.Assignment(dom)
```
現在,讓我們用`val`初始化模型`m`:
```py
>>> m = nltk.Model(dom, val)
```
每一個模型都有一個`evaluate()`方法,可以確定邏輯表達式,如命題邏輯的公式,的語義值;當然,這些值取決于最初我們分配給命題符號如`P`,`Q`和`R`的真值。
```py
>>> print(m.evaluate('(P & Q)', g))
True
>>> print(m.evaluate('-(P & Q)', g))
False
>>> print(m.evaluate('(P & R)', g))
False
>>> print(m.evaluate('(P | R)', g))
True
```
注意
**輪到你來:**做實驗為不同的命題邏輯公式估值。模型是否給出你所期望的值?
到目前為止,我們已經將我們的英文句子翻譯成命題邏輯。因為我們只限于用字母如`P`和`Q`表示原子句子,不能深入其內部結構。實際上,我們說將原子句子分成主語、賓語和謂詞并沒有語義上的好處。然而,這似乎是錯誤的:如果我們想形式化如[(9)](./ch10.html#ex-proplog8)這樣的論證,就必須要能“看到里面”基本的句子。因此,我們將超越命題邏輯到一個更有表現力的東西,也就是一階邏輯。這正是我們下一節要講的。
## 3 一階邏輯
本章的剩余部分,我們將通過翻譯自然語言表達式為一階邏輯來表示它們的意思。并不是所有的自然語言語義都可以用一階邏輯表示。但它是計算語義的一個不錯的選擇,因為它具有足夠的表現力來表達語義的很多方面,而且另一方面,有出色的現成系統可用于開展一階邏輯自動推理。
下一步我們將描述如何構造一階邏輯公式,然后是這樣的公式如何用來評估模型。
## 3.1 句法
一階邏輯保留所有命題邏輯的布爾運算符。但它增加了一些重要的新機制。首先,命題被分析成謂詞和參數,這將我們與自然語言的結構的距離拉近了一步。一階邏輯的標準構造規則承認以下術語:獨立變量和獨立常量、帶不同數量的參數的謂詞。例如,Angus walks 可以被形式化為 walk(angus),Angus sees Bertie 可以被形式化為 see(angus, bertie)。我們稱 walk 為一元謂詞,see 為二元謂詞。作為謂詞使用的符號不具有內在的含義,雖然很難記住這一點。回到我們前面的一個例子,[(13a)](./ch10.html#ex-predlog11)和[(13b)](./ch10.html#ex-predlog12)之間沒有邏輯區別。
```py
>>> read_expr = nltk.sem.Expression.fromstring
>>> expr = read_expr('walk(angus)', type_check=True)
>>> expr.argument
<ConstantExpression angus>
>>> expr.argument.type
e
>>> expr.function
<ConstantExpression walk>
>>> expr.function.type
<e,?>
```
為什么我們在這個例子的結尾看到`<e,?>`呢?雖然類型檢查器會嘗試推斷出盡可能多的類型,在這種情況下,它并沒有能夠推斷出`walk`的類型,所以其結果的類型是未知的。雖然我們期望`walk`的類型是`<e, t>`,迄今為止類型檢查器知道的,在這個上下文中可能是一些其他類型,如`<e, e>`或`<e, <e, t>`。要幫助類型檢查器,我們需要指定一個信號,作為一個字典來實施,明確的與非邏輯常量類型關聯:
```py
>>> sig = {'walk': '<e, t>'}
>>> expr = read_expr('walk(angus)', signature=sig)
>>> expr.function.type
e
```
一種二元謂詞具有類型?e, ?e, t??。雖然這是先組合類型 e 的一個參數成一個一元謂詞的類型,我們可以用二元謂詞的兩個參數直接組合來表示二元謂詞。例如,在<cite>Angus sees Cyril</cite>的翻譯中謂詞 see 會與它的參數結合得到結果 see(angus, cyril)。
在一階邏輯中,謂詞的參數也可以是獨立變量,如 x,y 和 z。在 NLTK 中,我們采用的慣例:_e_ 類型的變量都是小寫。獨立變量類似于人稱代詞,如 he,she 和 it ,其中我們為了弄清楚它們的含義需要知道它們使用的上下文。
解釋[(14)](./ch10.html#ex-predlog2)中的代名詞的方法之一是指向上下文中相關的個體。
```py
((exists x. dog(x)) -> bark(x))
```
## 3.2 一階定理證明
回顧一下我們較早前在[(10)](./ch10.html#ex-north)中提出的 to the north of 上的限制:
```py
all x. all y.(north_of(x, y) -> -north_of(y, x))
```
令人高興的是,定理證明器證明我們的論證是有效的。相反,它得出結論:不能從我們的假設推到出`north_of(f, s)`:
```py
>>> FnS = read_expr('north_of(f, s)')
>>> prover.prove(FnS, [SnF, R])
False
```
## 3.3 一階邏輯語言總結
我們將借此機會重新表述前面的命題邏輯的語法規則,并添加量詞的形式化規則;所有這些一起組成一階邏輯的句法。此外,我們會明確相關表達式的類型。我們將采取約定:?e<sup>n</sup>, t?一種由 n 個類型為 e 的參數組成產生一個類型為 t 的表達式的謂詞的類型。在這種情況下,我們說 n 是謂詞的元數。
> 1. If P is a predicate of type ?e<sup>n</sup>, t?, and α<sub>1</sub>, ... α<sub>n</sub> are terms of type e, then P(α<sub>1</sub>, ... α<sub>n</sub>) is of type t.
> 2. If α and β are both of type e, then (α = β) and (α != β) are of type t.
> 3. If φ is of type t, then so is `-`φ.
> 4. If φ and ψ are of type t, then so are (φ `&` ψ), (φ `|` ψ), (φ `->` ψ) and (φ `<->` ψ).
> 5. If φ is of type t, and x is a variable of type e, then `exists x.`φ and `all x.`φ are of type t.
[3.1](./ch10.html#tab-nltk-logic)總結了`logic`模塊的新的邏輯常量,以及`Expression`模塊的兩個方法。
表 3.1:
一階邏輯所需的新的邏輯關系和運算符總結,以及`Expression`類的兩個有用的方法。
```py
>>> dom = {'b', 'o', 'c'}
```
我們使用工具函數`Valuation.fromstring()`將 symbol `=>` value 形式的字符串序列轉換成一個`Valuation`對象。
```py
>>> v = """
... bertie => b
... olive => o
... cyril => c
... boy => {b}
... girl => {o}
... dog => {c}
... walk => {o, c}
... see => {(b, o), (c, b), (o, c)}
... """
>>> val = nltk.Valuation.fromstring(v)
>>> print(val)
{'bertie': 'b',
'boy': {('b',)},
'cyril': 'c',
'dog': {('c',)},
'girl': {('o',)},
'olive': 'o',
'see': {('o', 'c'), ('c', 'b'), ('b', 'o')},
'walk': {('c',), ('o',)}}
```
根據這一估值,`see`的值是一個元組的集合,包含 Bertie 看到 Olive、Cyril 看到 Bertie 和 Olive 看到 Cyril。
注意
**輪到你來:**模仿[1.2](./ch10.html#fig-model-kids)繪制一個圖,描述域`m`和相應的每個一元謂詞的集合。
你可能已經注意到,我們的一元謂詞(即`boy`,`girl`,`dog`)也是以單個元組的集合而不是個體的集合出現的。這使我們能夠方便的統一處理任何元數的關系。一個形式為 P(τ<sub>1</sub>, ... τ<sub>n</sub>)的謂詞,其中 P 是 n 元的,為真的條件是對應于(τ<sub>1</sub>, ... τ<sub>n</sub>) 的值的元組屬于 P 的值的元組的集合。
```py
>>> ('o', 'c') in val['see']
True
>>> ('b',) in val['boy']
True
```
## 3.5 獨立變量和賦值
在我們的模型,上下文的使用對應的是為變量賦值。這是一個從獨立變量到域中實體的映射。賦值使用構造函數`Assignment`,它也以論述的模型的域為參數。我們無需實際輸入任何綁定,但如果我們要這樣做,它們是以(變量,值)的形式來綁定,類似于我們前面看到的估值。
```py
>>> g = nltk.Assignment(dom, [('x', 'o'), ('y', 'c')])
>>> g
{'y': 'c', 'x': 'o'}
```
此外,還可以使用`print()`查看賦值,使用與邏輯教科書中經常出現的符號類似的符號:
```py
>>> print(g)
g[c/y][o/x]
```
現在讓我們看看如何為一階邏輯的原子公式估值。首先,我們創建了一個模型,然后調用`evaluate()`方法來計算真值。
```py
>>> m = nltk.Model(dom, val)
>>> m.evaluate('see(olive, y)', g)
True
```
這里發生了什么?我們正在為一個公式估值,類似于我們前面的例子`see(olive, cyril)`。然而,當解釋函數遇到變量`y`時,不是檢查`val`中的值,它在變量賦值`g`中查詢這個變量的值:
```py
>>> g['y']
'c'
```
由于我們已經知道`o`和`c`在 see 關系中表示的含義,所以`True`值是我們所期望的。在這種情況下,我們可以說賦值`g`滿足公式`see(olive, y)`。相比之下,下面的公式相對`g`的評估結果為`False`(檢查為什么會是你看到的這樣)。
```py
>>> m.evaluate('see(y, x)', g)
False
```
在我們的方法中(雖然不是標準的一階邏輯),變量賦值是部分的。例如,`g`中除了`x`和`y`沒有其它變量。方法`purge()`清除一個賦值中所有的綁定。
```py
>>> g.purge()
>>> g
{}
```
如果我們現在嘗試為公式,如`see(olive, y)`,相對于`g`估值,就像試圖解釋一個包含一個 him 的句子,我們不知道 him 指什么。在這種情況下,估值函數未能提供一個真值。
```py
>>> m.evaluate('see(olive, y)', g)
'Undefined'
```
由于我們的模型已經包含了解釋布爾運算的規則,任意復雜的公式都可以組合和評估。
```py
>>> m.evaluate('see(bertie, olive) & boy(bertie) & -walk(bertie)', g)
True
```
確定模型中公式的真假的一般過程稱為模型檢查。
## 3.6 量化
現代邏輯的關鍵特征之一就是變量滿足的概念可以用來解釋量化的公式。讓我們用[(24)](./ch10.html#ex-exists1)作為一個例子。
```py
>>> m.evaluate('exists x.(girl(x) & walk(x))', g)
True
```
在這里`evaluate()``True`,因為`dom`中有某些 _u_ 通過綁定`x`到 _u_ 的賦值滿足([(25)](./ch10.html#ex-exists2) )。事實上,`o`是這樣一個 _u_:
```py
>>> m.evaluate('girl(x) & walk(x)', g.add('x', 'o'))
True
```
NLTK 中提供了一個有用的工具是`satisfiers()`方法。它返回滿足開放公式的所有個體的集合。該方法的參數是一個已分析的公式、一個變量和一個賦值。下面是幾個例子:
```py
>>> fmla1 = read_expr('girl(x) | boy(x)')
>>> m.satisfiers(fmla1, 'x', g)
{'b', 'o'}
>>> fmla2 = read_expr('girl(x) -> walk(x)')
>>> m.satisfiers(fmla2, 'x', g)
{'c', 'b', 'o'}
>>> fmla3 = read_expr('walk(x) -> girl(x)')
>>> m.satisfiers(fmla3, 'x', g)
{'b', 'o'}
```
想一想為什么`fmla2`和`fmla3`是那樣的值,這是非常有用。`->`的真值條件的意思是`fmla2`等價于`-girl(x) | walk(x)`,要么不是女孩要么沒有步行的個體滿足條件。因為`b`(Bertie)和`c`(Cyril)都不是女孩,根據模型`m`,它們都滿足整個公式。當然`o`也滿足公式,因為`o`兩項都滿足。現在,因為話題的域的每一個成員都滿足`fmla2`,相應的全稱量化公式也為真。
```py
>>> m.evaluate('all x.(girl(x) -> walk(x))', g)
True
```
換句話說,一個全稱量化公式?x.φ關于`g`為真,只有對每一個 _u_,φ關于`g[u/x]`為真。
注意
**輪到你來:**先用筆和紙,然后用`m.evaluate()`,嘗試弄清楚`all x.(girl(x) & walk(x))`和`exists x.(boy(x) -> walk(x))`的真值。確保你能理解為什么它們得到這些值。
## 3.7 量詞范圍歧義
當我們給一個句子的形式化表示 _ 兩 _ 個量詞時,會發生什么?
```py
>>> v2 = """
... bruce => b
... elspeth => e
... julia => j
... matthew => m
... person => {b, e, j, m}
... admire => {(j, b), (b, b), (m, e), (e, m)}
... """
>>> val2 = nltk.Valuation.fromstring(v2)
```
admire 關系可以使用[(28)](./ch10.html#ex-admire-mapping)所示的映射圖進行可視化。
```py
>>> dom2 = val2.domain
>>> m2 = nltk.Model(dom2, val2)
>>> g2 = nltk.Assignment(dom2)
>>> fmla4 = read_expr('(person(x) -> exists y.(person(y) & admire(x, y)))')
>>> m2.satisfiers(fmla4, 'x', g2)
{'e', 'b', 'm', 'j'}
```
這表明`fmla4`包含域中每一個個體。相反,思考下面的公式`fmla5`;沒有滿足`y`的值。
```py
>>> fmla5 = read_expr('(person(y) & all x.(person(x) -> admire(x, y)))')
>>> m2.satisfiers(fmla5, 'y', g2)
set()
```
也就是說,沒有大家都欽佩的人。看看另一個開放的公式`fmla6`,我們可以驗證有一個人,即 Bruce,它被 Julia 和 Bruce 都欽佩。
```py
>>> fmla6 = read_expr('(person(y) & all x.((x = bruce | x = julia) -> admire(x, y)))')
>>> m2.satisfiers(fmla6, 'y', g2)
{'b'}
```
注意
**輪到你來:**基于`m2`設計一個新的模型,使[(27a)](./ch10.html#ex-scope2a)在你的模型中為假;同樣的,設計一個新的模型使[(27b)](./ch10.html#ex-scope2b)為真。
## 3.8 模型的建立
我們一直假設我們已經有了一個模型,并要檢查模型中的一個句子的真值。相比之下,模型的建立是給定一些句子的集合,嘗試創造一種新的模型。如果成功,那么我們知道集合是一致的,因為我們有模型的存在作為證據。
我們通過創建`Mace()`的一個實例并調用它的`build_model()`方法來調用 Mace4 模式產生器,與調用 Prover9 定理證明器類似的方法。一種選擇是將我們的候選的句子集合作為假設,保留目標為未指定。下面的交互顯示了`[a, c1]`和`[a, c2]`都是一致的列表,因為 Mace 成功的為它們都建立了一個模型,而`[c1, c2]`不一致。
```py
>>> a3 = read_expr('exists x.(man(x) & walks(x))')
>>> c1 = read_expr('mortal(socrates)')
>>> c2 = read_expr('-mortal(socrates)')
>>> mb = nltk.Mace(5)
>>> print(mb.build_model(None, [a3, c1]))
True
>>> print(mb.build_model(None, [a3, c2]))
True
>>> print(mb.build_model(None, [c1, c2]))
False
```
我們也可以使用模型建立器作為定理證明器的輔助。假設我們正試圖證明`S` ? `g`,即`g`是假設`S = [s1, s2, ..., sn]`的邏輯派生。我們可以同樣的輸入提供給 Mace4,模型建立器將嘗試找出一個反例,就是要表明`g`_ 不 _ 遵循從`S`。因此,給定此輸入,Mace4 將嘗試為假設`S`連同`g`的否定找到一個模型,即列表`S' = [s1, s2, ..., sn, -g]`。如果`g`從`S`不能證明出來,那么 Mace4 會返回一個反例,比 Prover9 更快的得出結論:無法找到所需的證明。相反,如果`g`從`S`是可以證明出來,Mace4 可能要花很長時間不能成功地找到一個反例模型,最終會放棄。
讓我們思考一個具體的方案。我們的假設是列表[There is a woman that every man loves, Adam is a man, Eve is a woman]。我們的結論是 Adam loves Eve。Mace4 能找到使假設為真而結論為假的模型嗎?在下面的代碼中,我們使用`MaceCommand()`檢查已建立的模型。
```py
>>> a4 = read_expr('exists y. (woman(y) & all x. (man(x) -> love(x,y)))')
>>> a5 = read_expr('man(adam)')
>>> a6 = read_expr('woman(eve)')
>>> g = read_expr('love(adam,eve)')
>>> mc = nltk.MaceCommand(g, assumptions=[a4, a5, a6])
>>> mc.build_model()
True
```
因此答案是肯定的:Mace4 發現了一個反例模型,其中 Adam 愛某個女人而不是 Eve。但是,讓我們細看 Mace4 的模型,轉換成我們用來估值的格式。
```py
>>> print(mc.valuation)
{'C1': 'b',
'adam': 'a',
'eve': 'a',
'love': {('a', 'b')},
'man': {('a',)},
'woman': {('a',), ('b',)}}
```
這個估值的一般形式應是你熟悉的:它包含了一些單獨的常量和謂詞,每一個都有適當類型的值。可能令人費解的是`C1`。它是一個“Skolem 常量”,模型生成器作為存在量詞的表示引入的。也就是說,模型生成器遇到`a4`里面的`exists y`,它知道,域中有某個個體`b`滿足`a4`中的開放公式。然而,它不知道`b`是否也是它的輸入中的某個地方的一個獨立常量的標志,所以它為`b`憑空創造了一個新名字,即`C1`。現在,由于我們的假設中沒有關于獨立常量`adam`和`eve`的信息,模型生成器認為沒有任何理由將它們當做表示不同的實體,于是它們都得到映射到`a`。此外,我們并沒有指定`man`和`woman`表示不相交的集合,因此,模型生成器讓它們相互重疊。這個演示非常明顯的隱含了我們用來解釋我們的情境的知識,而模型生成器對此一無所知。因此,讓我們添加一個新的假設,使 man 和 woman 不相交。模型生成器仍然產生一個反例模型,但這次更符合我們直覺的有關情況:
```py
>>> a7 = read_expr('all x. (man(x) -> -woman(x))')
>>> g = read_expr('love(adam,eve)')
>>> mc = nltk.MaceCommand(g, assumptions=[a4, a5, a6, a7])
>>> mc.build_model()
True
>>> print(mc.valuation)
{'C1': 'c',
'adam': 'a',
'eve': 'b',
'love': {('a', 'c')},
'man': {('a',)},
'woman': {('c',), ('b',)}}
```
經再三考慮,我們可以看到我們的假設中沒有說 Eve 是論域中唯一的女性,所以反例模型其實是可以接受的。如果想排除這種可能性,我們將不得不添加進一步的假設,如`exists y. all x. (woman(x) -> (x = y))`以確保模型中只有一個女性。
## 4 英語句子的語義
## 4.1 基于特征的語法中的合成語義學
在本章開頭,我們簡要說明了一種在句法分析的基礎上建立語義表示的方法,使用在[9.](./ch09.html#chap-featgram)開發的語法框架。這一次,不是構建一個 SQL 查詢,我們將建立一個邏輯形式。我們設計這樣的語法的指導思想之一是組合原則。(也稱為 Frege 原則;下面給出的公式參見[(Gleitman & Liberman, 1995)](./bibliography.html#partee1995lsc) 。)
**組合原則**:整體的含義是部分的含義與它們的句法結合方式的函數。
我們將假設一個復雜的表達式的語義相關部分由句法分析理論給出。在本章中,我們將認為表達式已經用上下文無關語法分析過。然而,這不是組合原則的內容。
我們現在的目標是以一種可以與分析過程平滑對接的方式整合語義表達的構建。[(29)](./ch10.html#ex-sem3)說明了我們想建立的這種分析的第一個近似。
```py
VP[SEM=?v] -> IV[SEM=?v]
NP[SEM=<cyril>] -> 'Cyril'
IV[SEM=<\x.bark(x)>] -> 'barks'
```
## 4.2 λ演算
在[3](./ch01.html#sec-computing-with-language-simple-statistics)中,我們指出數學集合符號對于制定我們想從文檔中選擇的詞的屬性 P 很有用。我們用[(31)](./ch10.html#ex-set-comprehension-math2)說明這個,它是“所有 w 的集合,其中 w 是 V(詞匯表)的元素且 w 有屬性 P”的表示。
```py
>>> read_expr = nltk.sem.Expression.fromstring
>>> expr = read_expr(r'\x.(walk(x) & chew_gum(x))')
>>> expr
<LambdaExpression \x.(walk(x) & chew_gum(x))>
>>> expr.free()
set()
>>> print(read_expr(r'\x.(walk(x) & chew_gum(y))'))
\x.(walk(x) & chew_gum(y))
```
我們對綁定表達式中的變量的結果有一個特殊的名字:λ-抽象。當你第一次遇到λ-抽象時,很難對它們的意思得到一個直觀的感覺。[(33b)](./ch10.html#ex-walk-chewgum12)的一對英語表示是“是一個 x,其中 x 步行且 x 嚼口香糖”或“具有步行和嚼口香糖的屬性。”通常認為λ-抽象可以很好的表示動詞短語(或無主語從句),尤其是當它作為參數出現在它自己的右側時。如[(34a)](./ch10.html#ex-walk-chewgum21)和它的翻譯[(34b)](./ch10.html#ex-walk-chewgum22)中的演示。
```py
(walk(x) & chew_gum(x))[gerald/x]
```
雖然我們迄今只考慮了λ-抽象的主體是一個某種類型 t 的開放公式,這不是必要的限制;主體可以是任何符合語法的表達式。下面是一個有兩個λ的例子。
```py
>>> print(read_expr(r'\x.\y.(dog(x) & own(y, x))(cyril)').simplify())
\y.(dog(cyril) & own(y,cyril))
>>> print(read_expr(r'\x y.(dog(x) & own(y, x))(cyril, angus)').simplify()) ![[1]](https://img.kancloud.cn/97/aa/97aa34f1d446f0c464068d0711295a9a_15x15.jpg)
(dog(cyril) & own(angus,cyril))
```
我們所有的λ-抽象到目前為止只涉及熟悉的一階變量:`x`、`y`等——類型 _e_ 的變量。但假設我們要處理一個抽象,例如`\x.walk(x)`作為另一個λ-抽象的參數?我們不妨試試這個:
```py
\y.y(angus)(\x.walk(x))
```
當β-約減在一個應用`f(a)`中實施時,我們檢查是否有自由變量在`a`同時也作為`f`的子術語中綁定的變量出現。假設在上面討論的例子中,`x`是`a`中的自由變量,`f`包括子術語`exists x.P(x)`。在這種情況下,我們產生一個`exists x.P(x)`的字母變體,也就是說,`exists z1.P(z1)`,然后再進行約減。這種重新標記由`logic`中的β-約減代碼自動進行,可以在下面的例子中看到的結果。
```py
>>> expr3 = read_expr('\P.(exists x.P(x))(\y.see(y, x))')
>>> print(expr3)
(\P.exists x.P(x))(\y.see(y,x))
>>> print(expr3.simplify())
exists z1.see(z1,x)
```
注意
當你在下面的章節運行這些例子時,你可能會發現返回的邏輯表達式的變量名不同;例如你可能在前面的公式的`z1`的位置看到`z14`。這種標簽的變化是無害的——事實上,它僅僅是一個字母變體的例子。
在此附注之后,讓我們回到英語句子的邏輯形式建立的任務。
## 4.3 量化的 NP
在本節開始,我們簡要介紹了如何為 Cyril barks 構建語義表示。你會以為這太容易了——肯定還有更多關于建立組合語義的。例如,量詞?沒錯,這是一個至關重要的問題。例如,我們要給出[(42a)](./ch10.html#ex-sem5a)的邏輯形式[(42b)](./ch10.html#ex-sem5b)。如何才能實現呢?
```py
>>> read_expr = nltk.sem.Expression.fromstring
>>> tvp = read_expr(r'\X x.X(\y.chase(x,y))')
>>> np = read_expr(r'(\P.exists x.(dog(x) & P(x)))')
>>> vp = nltk.sem.ApplicationExpression(tvp, np)
>>> print(vp)
(\X x.X(\y.chase(x,y)))(\P.exists x.(dog(x) & P(x)))
>>> print(vp.simplify())
\x.exists z2.(dog(z2) & chase(x,z2))
```
為了建立一個句子的語義表示,我們也需要組合主語`NP`的語義。如果后者是一個量化的表達式,例如 every girl,一切都與我們前面講過的 a dog barks 一樣的處理方式;主語轉換為函數表達式,這被用于`VP`的語義表示。然而,我們現在似乎已經用適當的名稱為自己創造了另一個問題。到目前為止,這些已經作為單獨的常量進行了語義的處理,這些不能作為像[(47)](./ch10.html#ex-sem99)那樣的表達式的函數應用。因此,我們需要為它們提出不同的語義表示。我們在這種情況下所做的是重新解釋適當的名稱,使它們也成為如量化的`NP`那樣的函數表達式。這里是 Angus 的λ表達式。
```py
>>> from nltk import load_parser
>>> parser = load_parser('grammars/book_grammars/simple-sem.fcfg', trace=0)
>>> sentence = 'Angus gives a bone to every dog'
>>> tokens = sentence.split()
>>> for tree in parser.parse(tokens):
... print(tree.label()['SEM'])
all z2.(dog(z2) -> exists z1.(bone(z1) & give(angus,z1,z2)))
```
NLTK 提供一些實用工具使獲得和檢查的語義解釋更容易。函數`interpret_sents()`用于批量解釋輸入句子的列表。它建立一個字典`d`,其中對每個輸入的句子`sent`,`d[sent]`是包含`sent`的分析樹和語義表示的(_synrep_, _semrep_)對的列表。該值是一個列表,因為`sent`可能有句法歧義;在下面的例子中,列表中的每個句子只有一個分析樹。
```py
>>> sents = ['Irene walks', 'Cyril bites an ankle']
>>> grammar_file = 'grammars/book_grammars/simple-sem.fcfg'
>>> for results in nltk.interpret_sents(sents, grammar_file):
... for (synrep, semrep) in results:
... print(synrep)
(S[SEM=<walk(irene)>]
(NP[-LOC, NUM='sg', SEM=<\P.P(irene)>]
(PropN[-LOC, NUM='sg', SEM=<\P.P(irene)>] Irene))
(VP[NUM='sg', SEM=<\x.walk(x)>]
(IV[NUM='sg', SEM=<\x.walk(x)>, TNS='pres'] walks)))
(S[SEM=<exists z3.(ankle(z3) & bite(cyril,z3))>]
(NP[-LOC, NUM='sg', SEM=<\P.P(cyril)>]
(PropN[-LOC, NUM='sg', SEM=<\P.P(cyril)>] Cyril))
(VP[NUM='sg', SEM=<\x.exists z3.(ankle(z3) & bite(x,z3))>]
(TV[NUM='sg', SEM=<\X x.X(\y.bite(x,y))>, TNS='pres'] bites)
(NP[NUM='sg', SEM=<\Q.exists x.(ankle(x) & Q(x))>]
(Det[NUM='sg', SEM=<\P Q.exists x.(P(x) & Q(x))>] an)
(Nom[NUM='sg', SEM=<\x.ankle(x)>]
(N[NUM='sg', SEM=<\x.ankle(x)>] ankle)))))
```
現在我們已經看到了英文句子如何轉換成邏輯形式,前面我們看到了在模型中如何檢查邏輯形式的真假。把這兩個映射放在一起,我們可以檢查一個給定的模型中的英語句子的真值。讓我們看看前面定義的模型`m`。工具`evaluate_sents()`類似于`interpret_sents()`,除了我們需要傳遞一個模型和一個變量賦值作為參數。輸出是三元組(_synrep_, _semrep_, _value_),其中 _synrep_、_semrep_ 和以前一樣,_value_ 是真值。為簡單起見,下面的例子只處理一個簡單的句子。
```py
>>> v = """
... bertie => b
... olive => o
... cyril => c
... boy => {b}
... girl => {o}
... dog => {c}
... walk => {o, c}
... see => {(b, o), (c, b), (o, c)}
... """
>>> val = nltk.Valuation.fromstring(v)
>>> g = nltk.Assignment(val.domain)
>>> m = nltk.Model(val.domain, val)
>>> sent = 'Cyril sees every boy'
>>> grammar_file = 'grammars/book_grammars/simple-sem.fcfg'
>>> results = nltk.evaluate_sents([sent], grammar_file, m, g)[0]
>>> for (syntree, semrep, value) in results:
... print(semrep)
... print(value)
all z4.(boy(z4) -> see(cyril,z4))
True
```
## 4.5 再述量詞歧義
上述方法的一個重要的限制是它們沒有處理范圍歧義。我們的翻譯方法是句法驅動的,認為語義表示與句法分析緊密耦合,語義中量詞的范圍也因此反映句法分析樹中相應的`NP`的相對范圍。因此,像[(26)](./ch10.html#ex-scope1)這樣的句子,在這里重復,總是會被翻譯為[(53a)](./ch10.html#ex-scope12a)而不是[(53b)](./ch10.html#ex-scope12b)。
```py
\P.exists y.(dog(y) & P(y))(\z2.chase(z1,z2))
```
最后,我們調用`s_retrieve()`檢查讀法。
```py
>>> cs_semrep.s_retrieve(trace=True)
Permutation 1
(\P.all x.(girl(x) -> P(x)))(\z2.chase(z2,z4))
(\P.exists x.(dog(x) & P(x)))(\z4.all x.(girl(x) -> chase(x,z4)))
Permutation 2
(\P.exists x.(dog(x) & P(x)))(\z4.chase(z2,z4))
(\P.all x.(girl(x) -> P(x)))(\z2.exists x.(dog(x) & chase(z2,x)))
```
```py
>>> for reading in cs_semrep.readings:
... print(reading)
exists x.(dog(x) & all z3.(girl(z3) -> chase(z3,x)))
all x.(girl(x) -> exists z4.(dog(z4) & chase(x,z4)))
```
## 5 段落語義層
段落是句子的序列。很多時候,段落中的一個句子的解釋依賴它前面的句子。一個明顯的例子來自照應代詞,如 he、she 和 it。給定一個段落如 Angus used to have a dog. But he recently disappeared.,你可能會解釋 he 指的是 Angus 的狗。然而,在 Angus used to have a dog. He took him for walks in New Town.中,你更可能解釋 he 指的是 Angus 自己。
## 5.1 段落表示理論
一階邏輯中的量化的標準方法僅限于單個句子。然而,似乎是有量詞的范圍可以擴大到兩個或兩個以上的句子的例子。。我們之前看到過一個,下面是第二個例子,與它的翻譯一起。
```py
([x, y], [angus(x), dog(y), own(x,y)])
```
我們可以使用`draw()`方法[![[1]](https://img.kancloud.cn/97/aa/97aa34f1d446f0c464068d0711295a9a_15x15.jpg)](./ch10.html#draw-drs)可視化結果,如[5.2](./ch10.html#fig-drs-screenshot)所示。
```py
>>> drs1.draw() ![[1]](https://img.kancloud.cn/97/aa/97aa34f1d446f0c464068d0711295a9a_15x15.jpg)
```
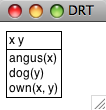
圖 5.2:DRS 截圖
我們討論[5.1](./ch10.html#fig-drs1)中 DRS 的真值條件時,假設最上面的段落指稱被解釋為存在量詞,而條件也進行了解釋,雖然它們是聯合的。事實上,每一個 DRS 都可以轉化為一階邏輯公式,`fol()`方法實現這種轉換。
```py
>>> print(drs1.fol())
exists x y.(angus(x) & dog(y) & own(x,y))
```
作為一階邏輯表達式功能補充,DRT`表達式`有 DRS-連接運算符,用`+`符號表示。兩個 DRS 的連接是一個單獨的 DRS 包含合并的段落指稱和來自兩個論證的條件。DRS-連接自動進行α-轉換綁定變量避免名稱沖突。
```py
>>> drs2 = read_dexpr('([x], [walk(x)]) + ([y], [run(y)])')
>>> print(drs2)
(([x],[walk(x)]) + ([y],[run(y)]))
>>> print(drs2.simplify())
([x,y],[walk(x), run(y)])
```
雖然迄今為止見到的所有條件都是原子的,一個 DRS 可以內嵌入另一個 DRS,這是全稱量詞被處理的方式。在`drs3`中,沒有頂層的段落指稱,唯一的條件是由兩個子 DRS 組成,通過蘊含連接。再次,我們可以使用`fol()`來獲得真值條件的句柄。
```py
>>> drs3 = read_dexpr('([], [(([x], [dog(x)]) -> ([y],[ankle(y), bite(x, y)]))])')
>>> print(drs3.fol())
all x.(dog(x) -> exists y.(ankle(y) & bite(x,y)))
```
我們較早前指出 DRT 旨在通過鏈接照應代詞和現有的段落指稱來解釋照應代詞。DRT 設置約束條件使段落指稱可以像先行詞那樣“可訪問”,但并不打算解釋一個特殊的先行詞如何被從候選集合中選出的。模塊`nltk.sem.drt_resolve_anaphora`采用了類此的保守策略:如果 DRS 包含`PRO(x)`形式的條件,方法`resolve_anaphora()`將其替換為`x = [...]`形式的條件,其中`[...]`是一個可能的先行詞列表。
```py
>>> drs4 = read_dexpr('([x, y], [angus(x), dog(y), own(x, y)])')
>>> drs5 = read_dexpr('([u, z], [PRO(u), irene(z), bite(u, z)])')
>>> drs6 = drs4 + drs5
>>> print(drs6.simplify())
([u,x,y,z],[angus(x), dog(y), own(x,y), PRO(u), irene(z), bite(u,z)])
>>> print(drs6.simplify().resolve_anaphora())
([u,x,y,z],[angus(x), dog(y), own(x,y), (u = [x,y,z]), irene(z), bite(u,z)])
```
由于指代消解算法已分離到它自己的模塊,這有利于在替代程序中交換,使對正確的先行詞的猜測更加智能。
我們對 DRS 的處理與處理λ-抽象的現有機制是完全兼容的,因此可以直接基于 DRT 而不是一階邏輯建立組合語義表示。這種技術在下面的不確定性規則(是語法`drt.fcfg`的一部分)中說明。為便于比較,我們已經從`simple-sem.fcfg`增加了不確定性的平行規則。
```py
Det[num=sg,SEM=<\P Q.(([x],[]) + P(x) + Q(x))>] -> 'a'
Det[num=sg,SEM=<\P Q. exists x.(P(x) & Q(x))>] -> 'a'
```
## 5.2 段落處理
我們解釋一句話時會使用豐富的上下文知識,一部分取決于前面的內容,一部分取決于我們的背景假設。DRT 提供了一個句子的含義如何集成到前面段落表示中的理論,但是在前面的討論中明顯缺少這兩個部分。首先,一直沒有嘗試納入任何一種推理;第二,我們只處理了個別句子。這些遺漏由模塊`nltk.inference.discourse`糾正。
段落是一個句子的序列 s<sub>1</sub>, ... s<sub>n</sub>,段落線是讀法的序列 s<sub>1</sub>-r<sub>i</sub>, ... s<sub>n</sub>-r<sub>j</sub> ,每個序列對應段落中的一個句子。該模塊按增量處理句子,當有歧義時保持追蹤所有可能的線。為簡單起見,下面的例子中忽略了范圍歧義。
```py
>>> dt = nltk.DiscourseTester(['A student dances', 'Every student is a person'])
>>> dt.readings()
s0 readings:
s0-r0: exists x.(student(x) & dance(x))
s1 readings:
s1-r0: all x.(student(x) -> person(x))
```
一個新句子添加到當前的段落時,設置參數`consistchk=True`會通過每條線,即每個可接受的讀法的序列的檢查模塊來檢查一致性。在這種情況下,用戶可以選擇收回有問題的句子。
```py
>>> dt.add_sentence('No person dances', consistchk=True)
Inconsistent discourse: d0 ['s0-r0', 's1-r0', 's2-r0']:
s0-r0: exists x.(student(x) & dance(x))
s1-r0: all x.(student(x) -> person(x))
s2-r0: -exists x.(person(x) & dance(x))
```
```py
>>> dt.retract_sentence('No person dances', verbose=True)
Current sentences are
s0: A student dances
s1: Every student is a person
```
以類似的方式,我們使用`informchk=True`檢查新的句子φ是否對當前的段落有信息量。定理證明器將段落線中現有的句子當做假設,嘗試證明φ;如果沒有發現這樣的證據,那么它是有信息量的。
```py
>>> dt.add_sentence('A person dances', informchk=True)
Sentence 'A person dances' under reading 'exists x.(person(x) & dance(x))':
Not informative relative to thread 'd0'
```
也可以傳遞另一套假設作為背景知識,并使用這些篩選出不一致的讀法;詳情請參閱`http://nltk.org/howto`上的段落 HOWTO。
`discourse`模塊可適應語義歧義,篩選出不可接受的讀法。下面的例子調用 Glue 語義和 DRT。由于 Glue 語義模塊被配置為使用的覆蓋面廣的 Malt 依存關系分析器,輸入(Every dog chases a boy. He runs.)需要分詞和標注。
```py
>>> from nltk.tag import RegexpTagger
>>> tagger = RegexpTagger(
... [('^(chases|runs)$', 'VB'),
... ('^(a)$', 'ex_quant'),
... ('^(every)$', 'univ_quant'),
... ('^(dog|boy)$', 'NN'),
... ('^(He)$', 'PRP')
... ])
>>> rc = nltk.DrtGlueReadingCommand(depparser=nltk.MaltParser(tagger=tagger))
>>> dt = nltk.DiscourseTester(['Every dog chases a boy', 'He runs'], rc)
>>> dt.readings()
s0 readings:
s0-r0: ([],[(([x],[dog(x)]) -> ([z3],[boy(z3), chases(x,z3)]))])
s0-r1: ([z4],[boy(z4), (([x],[dog(x)]) -> ([],[chases(x,z4)]))])
s1 readings:
s1-r0: ([x],[PRO(x), runs(x)])
```
段落的第一句有兩種可能的讀法,取決于量詞的作用域。第二句的唯一的讀法通過條件<cite>PRO(x)`</cite>表示代詞 He。現在讓我們看看段落線的結果:
```py
>>> dt.readings(show_thread_readings=True)
d0: ['s0-r0', 's1-r0'] : INVALID: AnaphoraResolutionException
d1: ['s0-r1', 's1-r0'] : ([z6,z10],[boy(z6), (([x],[dog(x)]) ->
([],[chases(x,z6)])), (z10 = z6), runs(z10)])
```
當我們檢查段落線`d0`和`d1`時,我們看到讀法`s0-r0`,其中 every dog 超出了`a boy`的范圍,被認為是不可接受的,因為第二句的代詞不能得到解釋。相比之下,段落線`d1`中的代詞(重寫為`z24`)_ 通過 _ 等式`(z24 = z20)`綁定。
不可接受的讀法可以通過傳遞參數`filter=True`過濾掉。
```py
>>> dt.readings(show_thread_readings=True, filter=True)
d1: ['s0-r1', 's1-r0'] : ([z12,z15],[boy(z12), (([x],[dog(x)]) ->
([],[chases(x,z12)])), (z17 = z12), runs(z15)])
```
雖然這一小段是極其有限的,它應該能讓你對于我們在超越單個句子后產生的語義處理問題,以及部署用來解決它們的技術有所了解。
## 6 小結
* 一階邏輯是一種適合在計算環境中表示自然語言的含義的語言,因為它很靈活,足以表示自然語言含義的很多有用的方面,具有使用一階邏輯推理的高效的定理證明器。(同樣的,自然語言語義中也有各種各樣的現象,需要更強大的邏輯機制。)
* 在將自然語言句子翻譯成一階邏輯的同時,我們可以通過檢查一階公式模型表述這些句子的真值條件。
* 為了構建成分組合的意思表示,我們為一階邏輯補充了λ-演算。
* λ-演算中的β-約簡在語義上與函數傳遞參數對應。句法上,它包括將被函數表達式中的λ綁定的變量替換為函數應用中表達式提供的參數。
* 構建模型的一個關鍵部分在于建立估值,為非邏輯常量分配解釋。這些被解釋為 _n_ 元謂詞或獨立常量。
* 一個開放表達式是一個包含一個或多個自由變量的表達式。開放表達式只在它的自由變量被賦值時被解釋。
* 量詞的解釋是對于具有變量 x 的公式φ[x],構建個體的集合,賦值 _g_ 分配它們作為 x 的值使φ[x]為真。然后量詞對這個集合加以約束。
* 一個封閉的表達式是一個沒有自由變量的表達式;也就是,變量都被綁定。一個封閉的表達式是真是假取決于所有變量賦值。
* 如果兩個公式只是由綁定操作符(即λ或量詞)綁定的變量的標簽不同,那么它們是α-等價。重新標記公式中的綁定變量的結果被稱為α-轉換。
* 給定有兩個嵌套量詞 _Q_<sub>1</sub>和 _Q_<sub>2</sub>的公式,最外層的量詞 _Q_<sub>1</sub>有較廣的范圍(或范圍超出 _Q_<sub>2</sub>)。英語句子往往由于它們包含的量詞的范圍而產生歧義。
* 在基于特征的語法中英語句子可以通過將`sem`作為特征與語義表達關聯。一個復雜的表達式的`sem`值通常包括成分表達式的`sem`值的函數應用。
## 7 深入閱讀
關于本章的進一步材料以及如何安裝 Prover9 定理證明器和 Mace4 模型生成器的內容請查閱`http://nltk.org/`。這兩個推論工具一般信息見[(McCune, 2008)](./bibliography.html#mccune)。
用 NLTK 進行語義分析的更多例子,請參閱`http://nltk.org/howto`上的語義和邏輯 HOWTO。請注意,范圍歧義還有其他兩種解決方法,即[(Blackburn & Bos, 2005)](./bibliography.html#blackburn2005rin)描述的 Hole 語義和[(Dalrymple, 1999)](./bibliography.html#dalrymple:1999:rrb)描述的 Glue 語義。
自然語言語義中還有很多現象沒有在本章中涉及到,主要有:
1. 事件、時態和體;
2. 語義角色;
3. 廣義量詞,如 most;
4. 內涵結構,例如像 may 和 believe 這樣的動詞。
(1)和(2)可以使用一階邏輯處理,(3)和(4)需要不同的邏輯。下面的讀物中很多都講述了這些問題。
建立自然語言前端數據庫方面的結果和技術的綜合概述可以在[(Androutsopoulos, Ritchie, & Thanisch, 1995)](./bibliography.html#androutsopoulos1995nli)中找到。
任何一本現代邏輯的入門書都將提出命題和一階邏輯。強烈推薦[(Hodges, 1977)](./bibliography.html#hodges1977l),書中有很多有關自然語言的有趣且有洞察力的文字和插圖。
要說范圍廣泛,參閱兩卷本的關于邏輯教科書[(Gamut, 1991)](./bibliography.html#gamut1991il)和[(Gamut, 1991)](./bibliography.html#gamut1991illg),也包含了有關自然語言的形式語義的當代材料,例如 Montague 文法和內涵邏輯。[(Kamp & Reyle, 1993)](./bibliography.html#kampreyle1993)提供段落表示理論的權威報告,包括涵蓋大量且有趣的自然語言片段,包括時態、體和形態。另一個對許多自然語言結構的語義的全面研究是[(Carpenter, 1997)](./bibliography.html#carpenter1997tls)。
有許多作品介紹語言學理論框架內的邏輯語義。[(Chierchia & McConnell-Ginet, 1990)](./bibliography.html#chierchia1990mg)與句法相對無關,而[(Heim & Kratzer, 1998)](./bibliography.html#heim1998sgg) and [(Larson & Segal, 1995)](./bibliography.html#larson1995km)都更明確的傾向于將語義真值條件整合到喬姆斯基框架中。
[(Blackburn & Bos, 2005)](./bibliography.html#blackburn2005rin)是致力于計算語義的第一本教科書,為該領域提供了極好的介紹。它擴展了許多本章涵蓋的主題,包括量詞范圍歧義的未指定、一階邏輯推理以及段落處理。
要獲得更先進的當代語義方法的概述,包括處理時態和廣義量詞,嘗試查閱[(Lappin, 1996)](./bibliography.html#lappin1996hcs)或[(Benthem & Meulen, 1997)](./bibliography.html#vanbenthem1997hll)。
## 8 練習
1. ? 將下列句子翻譯成命題邏輯,并用`Expression.fromstring()`驗證結果。提供顯示你的翻譯中命題變量如何對應英語表達的一個要點。
1. If Angus sings, it is not the case that Bertie sulks.
2. Cyril runs and barks.
3. It will snow if it doesn't rain.
4. It's not the case that Irene will be happy if Olive or Tofu comes.
5. Pat didn't cough or sneeze.
6. If you don't come if I call, I won't come if you call.
2. ? 翻譯下面的句子為一階邏輯的謂詞參數公式。
1. Angus likes Cyril and Irene hates Cyril.
2. Tofu is taller than Bertie.
3. Bruce loves himself and Pat does too.
4. Cyril saw Bertie, but Angus didn't.
5. Cyril is a fourlegged friend.
6. Tofu and Olive are near each other.
3. ? 翻譯下列句子為成一階邏輯的量化公式。
1. Angus likes someone and someone likes Julia.
2. Angus loves a dog who loves him.
3. Nobody smiles at Pat.
4. Somebody coughs and sneezes.
5. Nobody coughed or sneezed.
6. Bruce loves somebody other than Bruce.
7. Nobody other than Matthew loves somebody Pat.
8. Cyril likes everyone except for Irene.
9. Exactly one person is asleep.
4. ? 翻譯下列動詞短語,使用λ-抽象和一階邏輯的量化公式。
1. feed Cyril and give a capuccino to Angus
2. be given 'War and Peace' by Pat
3. be loved by everyone
4. be loved or detested by everyone
5. be loved by everyone and detested by no-one
5. ? 思考下面的語句:
```py
>>> read_expr = nltk.sem.Expression.fromstring
>>> e2 = read_expr('pat')
>>> e3 = nltk.sem.ApplicationExpression(e1, e2)
>>> print(e3.simplify())
exists y.love(pat, y)
```
顯然這里缺少了什么東西,即`e1`值的聲明。為了`ApplicationExpression(e1, e2)`被β-轉換為`exists y.love(pat, y)`,`e1`必須是一個以`pat`為參數的λ-抽象。你的任務是構建這樣的一個抽象,將它綁定到`e1`,使上面的語句都是滿足(上到字母方差)。此外,提供一個`e3.simplify()`的非正式的英文翻譯。
現在根據`e3.simplify()`的進一步情況(如下所示)繼續做同樣的任務。
```py
>>> print(e3.simplify())
exists y.(love(pat,y) | love(y,pat))
```
```py
>>> print(e3.simplify())
exists y.(love(pat,y) | love(y,pat))
```
```py
>>> print(e3.simplify())
walk(fido)
```
6. ? 如前面的練習中那樣,找到一個λ-抽象`e1`,產生與下面顯示的等效的結果。
```py
>>> e2 = read_expr('chase')
>>> e3 = nltk.sem.ApplicationExpression(e1, e2)
>>> print(e3.simplify())
\x.all y.(dog(y) -> chase(x,pat))
```
```py
>>> e2 = read_expr('chase')
>>> e3 = nltk.sem.ApplicationExpression(e1, e2)
>>> print(e3.simplify())
\x.exists y.(dog(y) & chase(pat,x))
```
```py
>>> e2 = read_expr('give')
>>> e3 = nltk.sem.ApplicationExpression(e1, e2)
>>> print(e3.simplify())
\x0 x1.exists y.(present(y) & give(x1,y,x0))
```
7. ? 如前面的練習中那樣,找到一個λ-抽象`e1`,產生與下面顯示的等效的結果。
```py
>>> e2 = read_expr('bark')
>>> e3 = nltk.sem.ApplicationExpression(e1, e2)
>>> print(e3.simplify())
exists y.(dog(x) & bark(x))
```
```py
>>> e2 = read_expr('bark')
>>> e3 = nltk.sem.ApplicationExpression(e1, e2)
>>> print(e3.simplify())
bark(fido)
```
```py
>>> e2 = read_expr('\\P. all x. (dog(x) -> P(x))')
>>> e3 = nltk.sem.ApplicationExpression(e1, e2)
>>> print(e3.simplify())
all x.(dog(x) -> bark(x))
```
8. ? 開發一種方法,翻譯英語句子為帶有二元廣義量詞的公式。在此方法中,給定廣義量詞`Q`,量化公式的形式為`Q(A, B)`,其中`A`和`B`是?_e_, _t_?類型的表達式。那么,例如`all(A, B)`為真當且僅當`A`表示的是`B`所表示的一個子集。
9. ? 擴展前面練習中的方法,使量詞如 most 和 exactly three 的真值條件可以在模型中計算。
10. ? 修改`sem.evaluate`代碼,使它能提供一個有用的錯誤消息,如果一個表達式不在模型的估值函數的域中。
11. ★ 從兒童讀物中選擇三個或四個連續的句子。一個例子是`nltk.corpus.gutenberg`中的故事集:`bryant-stories.txt`,`burgess-busterbrown.txt`和`edgeworth-parents.txt`。開發一個語法,能將你的句子翻譯成一階邏輯,建立一個模型,使它能檢查這些翻譯為真或為假。
12. ★ 實施前面的練習,但使用 DRT 作為意思表示。
13. [(Warren & Pereira, 1982)](./bibliography.html#warren1982eea)為出發點,開發一種技術,轉換一個自然語言查詢為一種可以更加有效的在模型中評估的形式。例如,給定一個`(P(x) & Q(x))`形式的查詢,將它轉換為`(Q(x) & P(x))`,如果`Q`的范圍比`P`小。
關于本文檔...
針對 NLTK 3.0 作出更新。本章來自于 _Natural Language Processing with Python_,[Steven Bird](http://estive.net/), [Ewan Klein](http://homepages.inf.ed.ac.uk/ewan/) 和[Edward Loper](http://ed.loper.org/),Copyright ? 2014 作者所有。本章依據 _Creative Commons Attribution-Noncommercial-No Derivative Works 3.0 United States License_ [[http://creativecommons.org/licenses/by-nc-nd/3.0/us/](http://creativecommons.org/licenses/by-nc-nd/3.0/us/)] 條款,與 _ 自然語言工具包 _ [`http://nltk.org/`] 3.0 版一起發行。
本文檔構建于星期三 2015 年 7 月 1 日 12:30:05 AEST
