Part10-物理動畫 · Canvas學習之旅

[TOC] ## 鍵盤事件在 Canvas 中，常用的鍵盤事件有兩種（1）鍵盤按下：keydown （2）鍵盤松開：keyup 鍵盤事件中一般都是根據按鍵的 keyCode 來判斷用戶按下的是鍵盤中的哪個鍵，常見的按鍵及其對應的 keyCode 如下表： | 按鍵 | keyCode | | --- | --- | | W | 87 | | S | 83 | | A | 65 | | D | 68 | | ↑ | 38 | | ↓ | 40 | | ← | 37 | | → | 39 | 我們先寫一個 tool.js 做一些封裝 ```js // 獲取鍵盤控制方向 window.tools.getKey = function () { var key = {} window.addEventListener('keydown', function (e) { if (e.keyCode === 38 || e.keyCode === 87) { key.direction = 'up' } else if (e.keyCode === 39 || e.keyCode === 68) { key.direction = 'right' } else if (e.keyCode === 40 || e.keyCode === 83) { key.direction = 'down' } else if (e.keyCode === 37 || e.keyCode === 65) { key.direction = 'left' } else { key.direction = '' } }, false) return key } ``` getKey() 方法返回一個對象 key，這個對象有一個 direction 屬性，表示用戶控制物體移動的方向。使用時只需要判斷 direction 屬性值是什么即可。 ```html <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8"> <meta name="viewport" content="width=device-width, initial-scale=1.0"> <meta http-equiv="X-UA-Compatible" content="ie=edge"> <title>鍵盤控制小球移動</title> <script src="./tool.js"></script> </head> <body> <canvas id="canvas" width="480" height="300" style="border: 1px solid gray; display: block; margin: 0 auto;"></canvas> <script> window.onload = function () { let cnv = document.getElementById('canvas') let cxt = cnv.getContext('2d') // 初始化一個圓形 drawBall(cnv.width / 2, cnv.height / 2) // 初始化變量 let x = 100 let y = 75 // 獲取按鍵方向 let key = tools.getKey() // 添加鼠標按下事件 window.addEventListener('keydown', function (e) { // 清除整個 Canvas，以重繪圖形 cxt.clearRect(0, 0, cnv.width, cnv.height) // 根據 key.direction 的值，判斷小球移動方向 switch (key.direction) { case 'up': y -= 2 drawBall(x, y) break case 'down': y += 2 drawBall(x, y) break case 'left': x -= 2 drawBall(x, y) break case 'right': x += 2 drawBall(x, y) break default: // 如果不加 default 按下其他按鍵小球就會消失了! drawBall(x, y) } }, false) // 定義繪制小球的函數 function drawBall (x, y) { cxt.beginPath() cxt.arc(x, y, 20, 0, 360 * Math.PI / 180, true) cxt.closePath() cxt.fillStyle = '#6699FF' cxt.fill() } } </script> </body> </html> ``` 這里先引入了 tool.js 文件，以便使用 getKey() 方法來獲取用戶控制小球的方向，然后使用 window.addEventListener() 來監聽鍵盤事件，根據 key.direction 的值來判斷小球移動的方向以實現控制小球的移動。 ## requestAnimationFrame() 的使用 Canvas 中一般都使用 requestAnimationFrame() 來實現循環，從而達到動畫效果，常見的語法如下，詳細解釋見 [MDN](https://developer.mozilla.org/zh-CN/docs/Web/API/Window/requestAnimationFrame) ```js (function frame () { window.requestAnimationFrame(frame) context.clearRect(0, 0, canvas.width, canvas.height) // ... })() ``` 這里定義了一個自執行函數 frame()，然后在函數內部使用 window.requestAnimationFrame() 不斷調用 frame()。對于 Canvas 動畫效果，每次必須清空畫布然后重繪才行，所以需要使用 clearRect() 方法清空畫布。 requestAnimationFrame() 方法的兼容代碼如下： ```js window.requestAnimationFrame = ( window.webkitRequestAnimationFrame || window.mozRequestAnimationFrame || window.msRequestAnimationFrame || window.oRequestAnimationFrame || function (callback) { return window.setTimeout(callback, 1000 / 60) } ) ``` ```html <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8"> <meta name="viewport" content="width=device-width, initial-scale=1.0"> <meta http-equiv="X-UA-Compatible" content="ie=edge"> <title>循環動畫</title> </head> <body> <canvas id="canvas" width="480" height="300" style="border: 1px solid gray; display: block; margin: 0 auto;"></canvas> <script> window.onload = function () { let cnv = document.getElementById('canvas') let cxt = cnv.getContext('2d') // 初始化圓的 x 軸坐標為 0 let x = 0; // 動畫循環 (function frame () { window.requestAnimationFrame(frame) cxt.clearRect(0, 0, cnv.width, cnv.height) // 繪制圓 cxt.beginPath() cxt.arc(x, 70, 20, 0, 360 * Math.PI / 180, true) cxt.closePath() cxt.fillStyle = 'skyblue' cxt.fill() // 變量遞增 x += 2 })() } </script> </body> </html> ``` ## 物理動畫物理動畫，簡單來說，就是模擬現實世界的一種動畫效果。在物理動畫中，物體會遵循牛頓運動定律。 ### 三角函數 ![](https://img.kancloud.cn/43/59/43595a3cd0ecefa813481c74d8a66280_529x283.png =400x) 對應 JavaScript 中的函數如下： - sin(θ)：Math.sin(θ * Math.PI / 180) - cos(θ)：Math.cos(θ * Math.PI / 180) - tan(θ)：Math.tan(θ * Math.PI / 180) - arcsin(x / R)：Math.asin(x / R) * (180 / Math.PI) - arccos(x / R): Math.acos(x / R) * (180 / Math.PI) - arctan(x / R): Math.atan(x / R) * (180 / Math.PI) 在 Canvas 中，凡是涉及角度都是用 “弧度制” 表示，例如 180° 寫成 Math.PI，360° 寫成 Math.PI * 2，所以角度都推薦下面這種寫法 ```js 度數 * Math.PI / 180 ``` <span style="font-size: 15px; font-weight: 600; color: #409EFF;">Math.atan() 與 Math.atan2()</span> 使用 Math.atan() 函數可能會出現有一個度數對應兩個夾角的情況，如圖（注意 canvas 中的坐標系）： ![](https://img.kancloud.cn/2a/88/2a88e7f930b9226df8d07860d9a7e018_952x607.png) 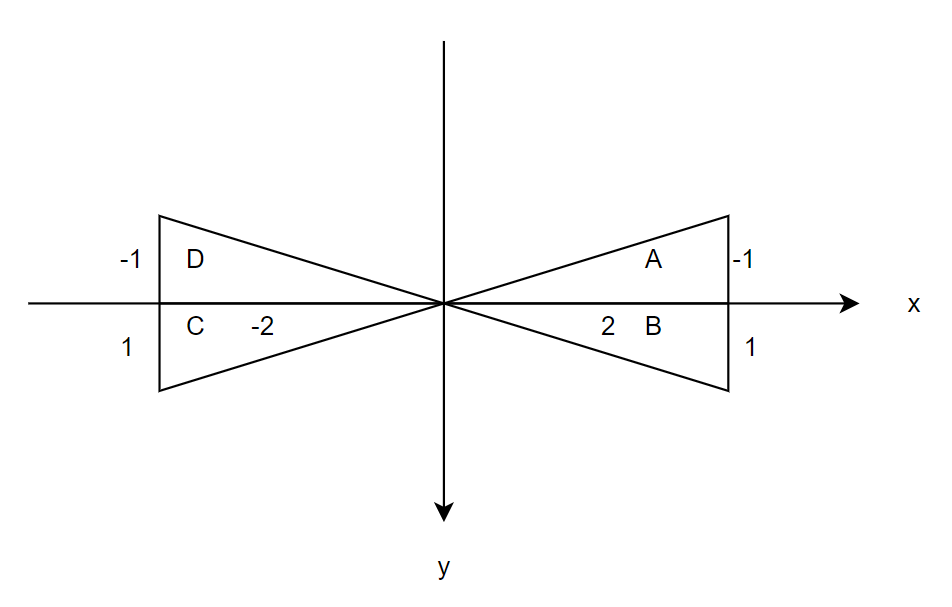對于上圖中的四個內角，將有以下正切值： tan(A) = tan(C) = -0.5 tan(B) = tan(D) = 0.5 為了解決這個問題，可以使用反正切函數 Math.atan2() 來求出兩條邊之間夾角的度數，并且能夠準確判斷度數對應哪一個夾角。 ![](https://img.kancloud.cn/47/7d/477d6bd16536cad48f463beaa976de64_452x191.png =300x) `Math.atan2(y, x)`接收兩個參數，y 表示對邊的變長，x 表示鄰邊的邊長 Math.atan(1 / 2) 和 Math.atan((-1) / (-2)) 的結果是一樣的，但是對于 Math.atan2() 函數而言，其結果是不同的。 ```js console.log(Math.atan2(1, 2), Math.atan2(-1, -2)) // 0.4636476090008061 -2.677945044588987 console.log(`Math.atan2(1, 2) 對應的角度為: ${Math.atan2(1, 2) * 180 / Math.PI} Math.atan2(-1, -2) 對應的角度為: ${Math.atan2(-1, -2) * 180 / Math.PI} `) // Math.atan2(1, 2) 對應的角度為: 26.56505117707799 // Math.atan2(-1, -2) 對應的角度為: -153.43494882292202 ``` ![](https://img.kancloud.cn/2a/88/2a88e7f930b9226df8d07860d9a7e018_952x607.png =400x) 可以看到 Math.atan2(1, 2) 對應的是角 B，而 Math.atan2(-1, -2) 對應的是角 D，-153。43° 這個角度是從 x 軸正方向開始以逆時針方向計算的，這樣就把兩個角區分開來了。 ![](https://img.kancloud.cn/3b/4c/3b4cc5c88e3f73e7757324aeb61bfd48_600x209.png =300x) 下面的示例是 Math.atan2() 的一個經典效果：追隨鼠標旋轉首先寫一個箭頭類 arrow.js 用于繪制箭頭 ```js Arrow.prototype = { stroke: function (cxt) { cxt.save() cxt.translate(this.x, this.y) cxt.rotate(this.angle) cxt.strokeStyle = this.color cxt.beginPath() cxt.moveTo(-20, -10) cxt.lineTo(0, -10) cxt.lineTo(0, -20) cxt.lineTo(20, 0) cxt.lineTo(0, 20) cxt.lineTo(0, 10) cxt.lineTo(-20, 10) cxt.closePath() cxt.stroke() cxt.restore() }, fill: function (cxt) { cxt.save() cxt.translate(this.x, this.y) cxt.rotate(this.angle) cxt.fillStyle = this.color cxt.beginPath() cxt.moveTo(-20, -10) cxt.lineTo(0, -10) cxt.lineTo(0, -20) cxt.lineTo(20, 0) cxt.lineTo(0, 20) cxt.lineTo(0, 10) cxt.lineTo(-20, 10) cxt.closePath() cxt.fill() cxt.restore() } } ``` ```html <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8"> <meta name="viewport" content="width=device-width, initial-scale=1.0"> <meta http-equiv="X-UA-Compatible" content="ie=edge"> <title>追隨鼠標旋轉</title> <script src="./arrow.js"></script> <script src="./tool.js"></script> </head> <body> <canvas id="canvas" width="480" height="300" style="border: 1px solid gray; display: block; margin: 0 auto;"></canvas> <script> window.onload = function () { let cnv = document.getElementById('canvas') let cxt = cnv.getContext('2d') // 實例化一個箭頭，中心坐標為畫布中心坐標 let arrow = new Arrow(cnv.width / 2, cnv.height / 2) // 獲取鼠標坐標 let mouse = tools.getMouse(cnv); // 這里記得加分號，封裝見 tools.js (function drawFrame () { window.requestAnimationFrame(drawFrame, cnv) cxt.clearRect(0, 0, cnv.width, cnv.height) let dx = mouse.x - cnv.width / 2 let dy = mouse.y - cnv.height / 2 // 使用 Math.atan2() 方法計算出鼠標與建投中心的夾角 arrow.angle = Math.atan2(dy, dx) arrow.fill(cxt) })() } </script> </body> </html> ``` ![](https://img.kancloud.cn/50/d0/50d003464ea2d321d869c4084c9f30c2_641x405.gif =300x) 效果：當鼠標在畫布上移動時，箭頭會跟著鼠標移動的方向進行旋轉。其原理很簡單，在動畫循環過程中，每次鼠標移動的時候，都會計算鼠標當前位置與箭頭中心的夾角，然后把這個夾角作為箭頭旋轉的角度，重繪箭頭即可。 ![](https://img.kancloud.cn/fa/8e/fa8e848b17a26ff022bb585a883ddc8f_396x323.png =200x) <span style="font-size: 15px; font-weight: 600; color: #409EFF;">圓周運動</span> Canvas 中的圓周運動一般有兩種，即正圓運動和橢圓運動。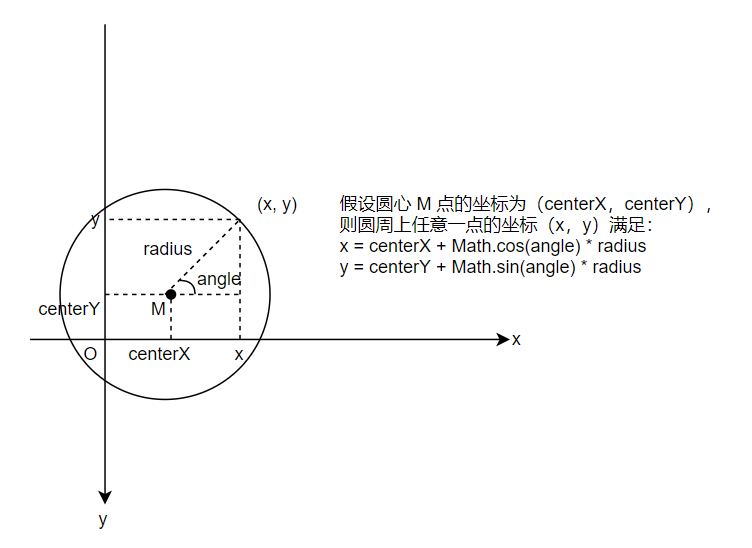 ![](https://img.kancloud.cn/51/13/5113d51659793de9362a4d666a4e54b3_752x548.png) 正圓運動就是利用上圖中的數學公式，下面做一個小球做正圓運動的例子：首先建立一個 ball.js 文件用于存放小球類： ```js function Ball (x, y, radius, color) { this.x = x || 0 this.y = y || 0 this.radius = radius || 12 this.color = color || '#6699FF' this.scaleX = 1 this.scaleY = 1 } Ball.prototype = { // 繪制 "描邊" 小球 stroke: function (cxt) { cxt.save() cxt.scale(this.scaleX, this.scaleY) cxt.strokeStyle = this.color cxt.beginPath() cxt.arc(this.x, this.y, this.radius, 0, 360 * Math.PI / 180, false) cxt.closePath() cxt.stroke() cxt.restore() }, // 繪制 "填充" 小球 fill: function (cxt) { cxt.save() cxt.translate(this.x, this.y) cxt.rotate(this.rotation) cxt.scale(this.scaleX, this.scaleY) cxt.fillStyle = this.color cxt.beginPath() cxt.arc(0, 0, this.radius, 0, 360 * Math.PI / 180, false) cxt.closePath() cxt.fill() cxt.restore() } } ``` 把圓的坐標公式套進去就能完成動畫了。 ```html <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8"> <meta name="viewport" content="width=device-width, initial-scale=1.0"> <meta http-equiv="X-UA-Compatible" content="ie=edge"> <title>正圓運動</title> <script src="./ball.js"></script> <script src="./tool.js"></script> </head> <body> <canvas id="canvas" width="480" height="300" style="border: 1px solid gray; display: block; margin: 0 auto;"></canvas> <script> window.onload = function () { let cnv = document.getElementById('canvas') let cxt = cnv.getContext('2d') // 實例化一個小球，中心坐標為 (100, 25)，半徑、顏色都取默認值 let ball = new Ball(100, 25) let centerX = cnv.width / 2 let centerY = cnv.height / 2 let radius = 50 let angle = 0; (function frame () { window.requestAnimationFrame(frame) cxt.clearRect(0, 0, cnv.width, cnv.height) // 繪制圓形 cxt.beginPath() cxt.arc(centerX, centerY, 50, 0, 360 * Math.PI / 180, false) cxt.closePath() cxt.stroke() // 計算小球坐標 ball.x = centerX + Math.cos(angle) * radius ball.y = centerY + Math.sin(angle) * radius ball.fill(cxt) // 角度遞增 angle += 0.05 })() } </script> </body> </html> ``` ![](https://img.kancloud.cn/15/21/15210546e03269527a07e185643f276a_641x405.gif =300x) <span style="font-size: 15px; font-weight: 600; color: #409EFF;">橢圓運動</span> ![](https://img.kancloud.cn/19/d7/19d7e429531964f088352dcc43698844_934x656.png) 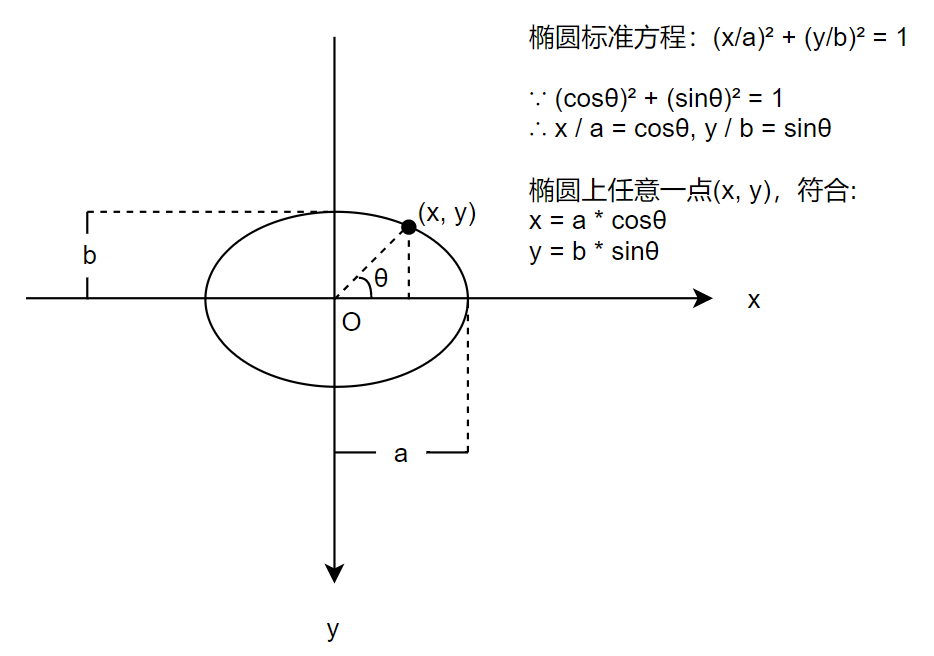總之就是把上面的公式套進去即可，代碼略作修改： ```js ball.x = centerX + Math.cos(angle) * radiusX ball.y = centerY + Math.sin(angle) * radiusY ``` ![](https://img.kancloud.cn/57/ed/57edd6f8807bdcd5e10761b4ec41d650_641x405.gif =300x) <span style="font-size: 15px; font-weight: 600; color: #409EFF;">波形運動</span> 正弦函數 sin 和余弦函數 cos 都有屬于它們自身的波形，由于它倆是相似的，這里僅以 sin 函數為例介紹。在 Canvas 中，根據 sin 函數作用對象的不同，常見的波形運動可以分為三種（1）作用于 x 軸坐標（2）作用于 y 軸坐標（3）作用于縮放屬性（scaleX 或 scaleY） 1、作用于 x 軸坐標當正弦函數作用于物體中心的 x 軸坐標時，物體會進行左右搖擺，類似于水草在水流中左右搖擺語法： ```js x = centerX + Math.sin(angle) * range angel += speed ``` 其中，（centerX，centerY）表示物體中心坐標，angle 表示角度（弧度制），range 表示振幅，speed 表示角度改變的大小。 ```html <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8"> <meta name="viewport" content="width=device-width, initial-scale=1.0"> <meta http-equiv="X-UA-Compatible" content="ie=edge"> <title>正圓運動</title> <script src="./ball.js"></script> <script src="./tool.js"></script> </head> <body> <canvas id="canvas" width="480" height="300" style="border: 1px solid gray; display: block; margin: 0 auto;"></canvas> <script> window.onload = function () { let cnv = document.getElementById('canvas') let cxt = cnv.getContext('2d') let ball = new Ball(cnv.width / 2, cnv.height / 2) let angle = 0 let range = 80; (function frame () { window.requestAnimationFrame(frame) cxt.clearRect(0, 0, cnv.width, cnv.height) // 計算小球坐標 ball.x = cnv.width / 2 + Math.sin(angle) * range ball.fill(cxt) // 角度遞增 angle += 0.05 })() } </script> </body> </html> ``` ![](https://img.kancloud.cn/49/a1/49a19834e2eee972c06a9f3e416e665f_641x405.gif =300x) 當正弦函數 sin 只作用于物體的 x 軸坐標時，就可以實現類似水草擺動的平滑運動效果。如果想使擺動的幅度看起來更明顯一些，可以乘以一個較大的值（振幅）。 2、作用于 y 軸坐標當正弦函數 sin 作用于物體中心的 y 軸坐標時，物體運動的軌跡剛好就是 sin 函數的波形語法： ```js y = centerY + Math.sin(angle) * rangel angle += speed ``` ```js ball.x += 1 ball.y = cnv.height / 2 + Math.sin(angle) * range ball.fill(cxt) ``` ![](https://img.kancloud.cn/b8/cf/b8cf78b24c1012e96c789d9ae5542dbc_641x405.gif =300x) 3、作用于縮放屬性（scaleX 或 scaleY）當正弦函數 sin 作用于物體的縮放屬性時，物體會不斷地放大然后縮小，從而產生一種脈沖動畫的效果。語法： ```js scaleX = 1 + Math.sin(angle) * range scaleY = 1 + Math.sin(angle) * range angle += speed ``` ```html <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8"> <meta name="viewport" content="width=device-width, initial-scale=1.0"> <meta http-equiv="X-UA-Compatible" content="ie=edge"> <title>sin 函數作用于縮放屬性</title> <script src="./ball.js"></script> <script src="./tool.js"></script> </head> <body> <canvas id="canvas" width="480" height="300" style="border: 1px solid gray; display: block; margin: 0 auto;"></canvas> <script> window.onload = function () { let cnv = document.getElementById('canvas') let cxt = cnv.getContext('2d') let ball = new Ball(cnv.width / 2, cnv.height / 2, 25) let range = 0.5 let angle = 0; (function frame () { window.requestAnimationFrame(frame) cxt.clearRect(0, 0, cnv.width, cnv.height) ball.scaleX = 1 + Math.sin(angle) * range ball.scaleY = 1 + Math.sin(angle) * range ball.fill(cxt) // 角度遞增 angle += 0.05 })() } </script> </body> </html> ``` ![](https://img.kancloud.cn/71/a2/71a2676386a619514eb5b589a9af4ecd_641x405.gif =300x) ### 勻速運動勻速運動是一種加速度為 0 的運動，比較簡單，語法如下： ```js object.x += vx object.y += vy ``` 其中，object.x 表示物體 x 軸坐標，object.y 表示物體 y 軸坐標。vx 表示 x 軸方向的速度大小，vy 表示 y 軸方向的速度大小。如果我們想在任意方向上做勻速運動該怎么做呢？這就需要用到速度的合成與分解。 ![](https://img.kancloud.cn/ce/a6/cea6cda4aa3d44ce0b8e83085510e9b8_747x417.png =400x) 語法： ```js vx = speed * Math.cos(angle * Math.PI / 180) vy = speed * Math.sin(angle * Math.PI / 180) object.x += vx object.y += vy ``` 下面是一個箭頭追隨鼠標勻速移動的例子： ```html <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8"> <meta name="viewport" content="width=device-width, initial-scale=1.0"> <meta http-equiv="X-UA-Compatible" content="ie=edge"> <title>箭頭追隨鼠標移動</title> <script src="./arrow.js"></script> <script src="./tool.js"></script> </head> <body> <canvas id="canvas" width="480" height="300" style="border: 1px solid gray; display: block; margin: 0 auto;"></canvas> <script> window.onload = function () { let cnv = document.getElementById('canvas') let cxt = cnv.getContext('2d') // 實例化一個箭頭，中心坐標為畫布中心坐標 let arrow = new Arrow(cnv.width / 2, cnv.height / 2) // 獲取鼠標坐標 let mouse = tools.getMouse(cnv) let speed = 1.5 let angle = 0; (function drawFrame () { window.requestAnimationFrame(drawFrame, cnv) cxt.clearRect(0, 0, cnv.width, cnv.height) let dx = mouse.x - cnv.width / 2 let dy = mouse.y - cnv.height / 2 // 使用 Math.atan2() 方法計算出鼠標與箭頭中心的夾角 angle = Math.atan2(dy, dx) let vx = Math.cos(angle) * speed let vy = Math.sin(angle) * speed arrow.x += vx arrow.y += vy arrow.angle = angle arrow.fill(cxt) })() } </script> </body> </html> ``` ![](https://img.kancloud.cn/42/36/4236777e2b01f12f8305d9931cc599ce_641x405.gif =300x) ### 加速運動勻速運動的速度大小是一直保持不變的，而加速運動的速度大小是會隨著時間變化而變化的。語法： ```js vx += ax // ax 表示 x 軸方向加速度 vy += ay object.x += vx object.y += vy ``` 同樣的，想做任意方向上的加速度就需要用到加速度的合成與分解。 ![](https://img.kancloud.cn/ea/f5/eaf50397b16a8531ec428705ea3c2729_620x313.png =300x) 語法： ```js ax = a * Math.cos(angle * Math.PI / 180) ay = a * Math.sin(angle * Math.PI / 180) vx += ax vy += ay object.x += vx object.y += vy ``` ### 重力語法： ```js vy += gravity object.y += vy ``` 對于重力引起的運動，可以看成是沿著 y 軸正方向的加速運動。利用重力的一個常見的效果就是自由落體反彈的效果，例子如下： ```html <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8"> <meta name="viewport" content="width=device-width, initial-scale=1.0"> <meta http-equiv="X-UA-Compatible" content="ie=edge"> <title>重力應用</title> <script src="./ball.js"></script> <script src="./tool.js"></script> </head> <body> <canvas id="canvas" width="480" height="300" style="border: 1px solid gray; display: block; margin: 0 auto;"></canvas> <script> window.onload = function () { let cnv = document.getElementById('canvas') let cxt = cnv.getContext('2d') let ball = new Ball(cnv.width / 2, 0) // y 軸初始速度為 0，重力加速度為 0.2，反彈系數為 -0.8 let vy = 0 const gravity = 0.2 const bounce = -0.8; (function drawFrame () { window.requestAnimationFrame(drawFrame) cxt.clearRect(0, 0, cnv.width, cnv.height) ball.y += vy // 邊界檢測 if (ball.y > cnv.height - ball.radius) { ball.y = cnv.height - ball.radius // 速度反向并且減小 vy = vy * bounce } ball.fill(cxt) // 變量遞增，注意放在圖形繪制之后 vy += gravity })() } </script> </body> </html> ``` ![](https://img.kancloud.cn/bb/07/bb07d38db1c1f3563bedbab24b9ad420_641x405.gif =300x) 小球碰到地面一般都會反彈，由于反彈會有速度損耗，并且小球 y 軸速度方向會變為反方向，因此需要乘以一個反彈系數 bounce，其取值一般為 -1.0 ~ 0 之間的任意數。 ### 摩擦力摩擦力指的是阻礙物體相對運動的力，其方向與物體運動的方向相反。摩擦力只會改變速度的大小而不會改變它的方向，即摩擦力只能將物體的速度降為 0，但它無法讓物體掉頭往相反的方向移動。語法： ```js vx *= friction // 摩擦系數 vy *= friction object.x += vx object.y += vy ``` 需要注意的是，當物體沿任意方向運動時，如果加入摩擦力因素，那么每次都應該先把該方向的速度分解為 x 軸和 y 軸兩個方向的分速度，然后再用分速度乘以摩擦系數，而不是分解摩擦力。