[TOC] > 計算機中是以補碼進行計算，原碼進行顯示 > 正數的反碼補碼都是其本身 > 負數的反碼是原碼符號位不變其他取反，補碼是反碼+1 * 對于計算機, 加減乘數已經是最基礎的運算, 要設計的盡量簡單. 計算機辨別"符號位"顯然會讓計算機的基礎電路設計變得十分復雜! 于是人們想出了將符號位也參與運算的方法. 我們知道, 根據運算法則減去一個正數等于加上一個負數, 即: 1-1 = 1 + (-1) = 0 * 計算機存儲的就是補碼，使用補碼進行運算免去了符號位帶來的麻煩 * 在計算機內，定點數有3種表示法：**原碼、反碼和補碼** * 原碼就是二進制定點表示法，即最高位為符號位，“0”表示正，“1”表示負，其余位表示數值的大小。 ## 1. 二進制 計算機的存儲全是01的二進制，最小單位是byte（8位） **+21，其二進制表示形式是00010101，則其補碼同樣為00010101** **-21的表示方式** 1. 按照概念其**絕對值為00010101**，各位**取反為11101010**，**再加1**為11101011，即-21的二進制表示形式為11101011 **1. byte為一字節8位，最高位是符號位，即最大值是01111111，因正數的補碼是其本身，即此正數為01111111** 2. 10000000是最小負數的補碼表示形式，我們把補碼計算步驟倒過來就即可。10000000減1得01111111然后取反10000000 因為負數的補碼是其絕對值取反，即10000000為最小負數的絕對值，而10000000的十進制表示是128，所以最小負數是-128 ## 1. 八進制 以0開頭 ## 2. 十六進制 以0x開頭，1-F，一個數字代表四位 f代表15，二進制表示00001111 ## 3. 練習題  ``` 0Xf000000000000000補碼為1111000000000000000000000000000000000000000000000000000000000000 0x7FFFFFFFFFFFFFFF補碼為0111111111111111111111111111111111111111111111111111111111111111 a-b=a+(-b)= 1111000000000000000000000000000000000000000000000000000000000000+ 1000000000000000000000000000000000000000000000000000000000000001= 10111000000000000000000000000000000000000000000000000000000000001(高位溢出舍去) 則結果為 0111000000000000000000000000000000000000000000000000000000000001= 2^62+2^61+2^60+1 ``` 答案為C ## 1-2 的二進制運算 1的原反補碼都相同，都是 0000 0001 -2 的原碼是 1000 0010 補碼是符號位不變，取反 1111 1101 加1 1111 1110 ``` 0000 0001 + 1111 1110 = 1111 1111 ``` 結果是負數，減一取反，得到原碼 1000 0001 即為-1 ## 練習 ~~~java System.out.println((byte) 129); System.out.println((byte) -129); System.out.println("~b2: " + ~10); ~~~ 結果是： ~~~ -127 127 ~b2: -11 ~~~ **計算機中是以補碼進行計算** 正數的反碼補碼都是原碼，如： 10 原碼: `1010` 反碼: `1010` 補碼：`1010` 負數 -10 原碼 `10000000 00000000 00000000 00001010` 反碼(符號位不變，其余位取反) `01111111 11111111 11111111 11110101` 補碼(反碼+1)： `01111111 11111111 11111111 11110110` ### (byte) 129 對于129，二進制為 `00000000 00000000 00000000 10000001` 其補碼：`00000000 00000000 00000000 10000001` 由于byte只占1字節即8位，所以，上面截取8位置后如下：`10000001` 此時最高位為1即負數，該二進制減1即是反碼 反碼：`10000000` 原碼：`11111111` 即-127，所以`(byte)129`的結果就是`-127` ### (byte) -129 \-129 二進制為 原碼：`10000000 00000000 00000000 10000001` 反碼（原碼符號位不變，其余取反）：`11111111 11111111 11111111 01111110` 補碼為(反碼+1) ： `11111111 11111111 11111111 01111111` 截取8位（低八位）后為：`01111111` 為正數，其原碼反碼補碼均為`01111111`即127 所以`(byte)-129`的結果就是`127` ### ~10 10的二進制為 `00000000 00000000 00000000 00001010` 補碼是本身，取反之后為 `11111111 11111111 11111111 11110101` 此時最高位為1，負數，即是負數的補碼 該反碼(補碼-1) `11111111 11111111 11111111 11110100` 對應的原碼： `10000000 00000000 00000000 00001011` 即-11 所以`~b2`的結果是`-11` ## 4. 字節運算 ## 4.1 與運算符 與運算符用符號“&”表示，其使用規律如下： 兩個操作數中位都為1，結果才為1，否則結果為0，例如下面的程序段。 聲明并初始化: int a = 10; int b = 6; 二進制: a = 0000 1010 b = 0000 0110 結算結果： 0000 0010 轉化為十進制： 2 ### 4.2 或運算符 或運算符用符號“|”表示，其運算規律如下： 兩個位只要有一個為1，那么結果就是1，否則就為0， 聲明并初始化: int a = 10; int b = 6; 二進制: a = 0000 1010 b = 0000 0110 結算結果： 0000 1110 轉化為十進制： 14 ### 4.3 異或運算符 異或運算符是用符號“^”表示的，其運算規律是： 兩個操作數的位中，相同則結果為0，不同則結果為1。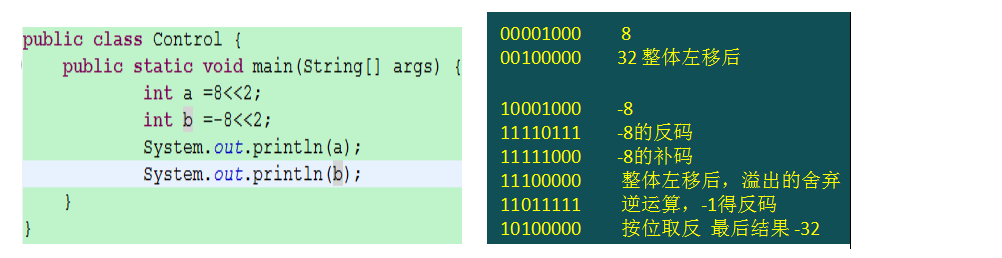 聲明并初始化: int a = 10; int b = 6; 二進制: a = 0000 1010 b = 0000 0110 結算結果： 0000 1100 轉化為十進制： 10 ### 4.4 非運算， 按位取反 ~5 非運算 補碼是： 00000101 補碼取反（非）： 11111010 補碼轉反碼-1： 11111001 反碼轉原碼(最高位為1，負數)：10000110 結果： -6 ## 5.字節位移 ### 5.1 左移 （<< ） ?右邊空出的位用0填補高位左移溢出則舍棄該高位。計算機中常用補碼表示數據，注，用補碼計算  ### 5.2 右移 （>> ） ?左邊空出的位用0或者1填補。正數用0填補，負數用1填補。注：不同的環境填補方式可能不同；低位右移溢出則舍棄該位。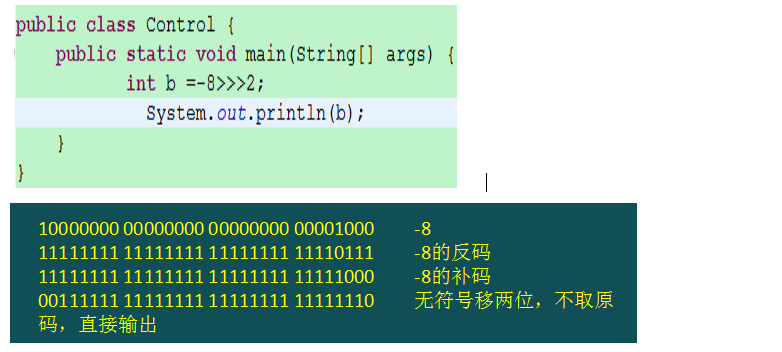  ### 5.3 無符號右 、移 （>>> ） ?無符號右移：正數與右移規則一樣，負數的無符號右移，就是相應的補碼移位所得，在高位補0即可（右移后，高位0，都是正數，所以得到的就是原碼=補碼=反碼），直接輸出