數據結構大致包含以下幾種存儲結構： **線性表**：零個或多個數據元素的有限序列 還可細分為順序表（底層實現靠數組）、鏈表、棧和隊列；棧和隊列隸屬于線性表，是特殊的線性表。 元素有多個時，第一個元素無前驅，最后一個無后繼，其他每個元素都有且只有一個前驅和后繼。 **樹結構**：包括普通樹，二叉樹，線索二叉樹等； **圖存儲結構** ## 數組、順序表（順序存儲結構） 順序存儲：一段地址連續的存儲單元依次存儲線性表的數據元素。 三個重要屬性： **起始位置、最大存儲容量、當前長度** 查詢的時間復雜度 o（1） 插入和刪除的復雜度是o（n）。 ? 插入時，后面的數據都要往后移動，刪除時，后面的數據都要往前移動 **優點：** 可以快速的存取表中任一位置的元素。 不需要為表示元素之間的邏輯關系而增加額外存儲空間。 **缺點：** 插入和刪除操作需要移動大量元素、性能受損 當元素數量變化較大，難以確定最大存儲容量 造成存儲空間的“碎片” 順序表底層就是使用數組。 ## 鏈表、鏈式存儲結構 鏈式存儲：地址可以連續也可以不連續的存儲單元存儲數據元素 數據域：存儲數據元素信息的域 指針域：存儲直接后繼位置的域（后一個元素的地址） 數據域 + 指針域 ?就是結點 ### 單鏈表 單鏈表：鏈表中的每個結點中只包含一個指針域 頭指針：鏈表中第一個結點的存儲位置 頭結點：有時會為了方便，會在單鏈表的第一個結點前附設一個節點，就是頭結點，頭結點的數據域可以不存儲任何信息。 頭指針和頭結點的區別： 頭指針是指鏈表指向第一個結點的指針，若鏈表有頭結點，則是指向頭結點的指針 頭指針具有標識作用，所以常用頭指針冠以鏈表的名字 無論鏈表是否為空，頭指針均不為空。頭指針是鏈表的必要元素 頭結點是為了操作的統一和方便而設立的，放在第一個元素的結點之前，其數據域一般無意義。 有了頭結點，對在第一個元素節點前插入結點和刪除第一個結點，其操作與其他結點的操作就統一了。 頭結點不一定是鏈表必須要素 查詢的時間復雜度 o（1）到o（n） ，查第一個就是o（1），最壞的情況是 o（n） 插入和刪除的復雜度，當知道元素的指針位置時是o（1），否則需要先查詢，復雜度則變成o（n）。 ? 插入和刪除越頻繁的操作，單鏈表的效率優勢就越是明顯。 工作指針后移 ## 順序存儲結構和單鏈表存儲結構的區別 * 存儲分配方式： * 順序存儲結構用一段連續的存儲單元依次存儲線性表的數據元素。 * 單鏈表采用鏈式存儲結構，用一組任意的存儲單元存放線性表的元素。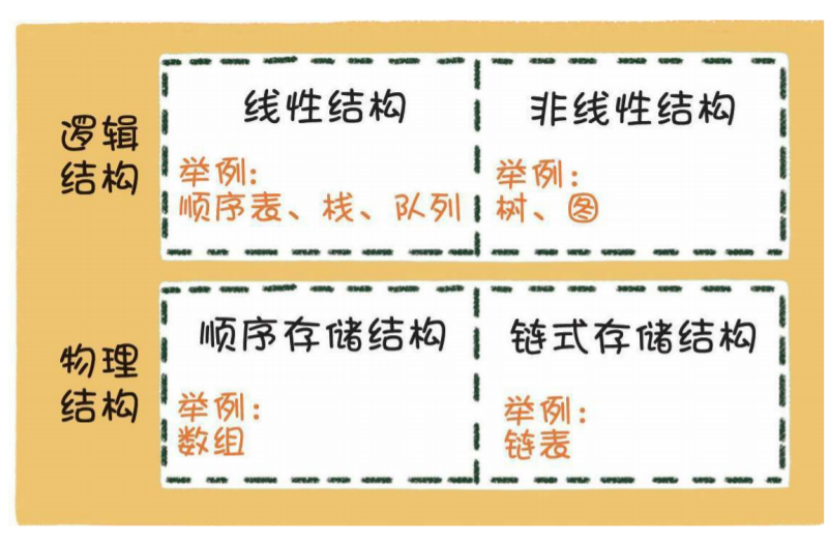 * 時間性能： * 查找： * 順序存儲結構O(1) * 單鏈表O(n) * 插入和刪除 * 順序存儲結構需要平均移動表長一半的元素，時間為O(n) * 單鏈表在線出某位置的指針后，插入和刪除時間僅為O(1) * 空間性能 * 順序存儲需要預分配存儲空間，分大了浪費，分小了易發生上溢 * 單鏈表不需要分配存儲空間，只要有就可以分配，元素個數也不受限制 結論： **插入和刪除頻繁的使用單鏈表結構，頻繁查找的使用順序存儲結構** **元素個數變化較大或根本無法確定可能的個數范圍，最好考慮單鏈表，這樣不需要考慮存儲空間的大小** ## 邏輯結構和物理結構  ## 棧 棧是限定僅在表尾進行插入和刪除操作的線性表。 我們把允許**插入和刪除的一端稱為棧頂**(top)，**另一端稱為棧底**(bottom)，不含任何數據元素的棧稱為空棧。棧又稱為后進先出(Last In First Out)的線性表，簡稱LIFO結構。 棧元素也具有線性關系，棧是一種特殊的線性表。定義中說是在線性表的表尾插入和刪除操作，這里表尾是指棧頂，而不是棧底。特殊在于限制了這個線性表的插入和刪除位置，只在棧頂進行。 棧的插入操作，叫作進棧，也稱壓棧、入棧。類似子彈入彈夾。 棧的刪除操作,叫作出棧,也有的叫作彈棧。如同彈夾中的子彈出夾。 ## 隊列 隊列是只允許在一端進行插入操作、而在另一端進行刪除操作的線性表。 隊列是一種先進先出(First In First Out)的線性表,簡稱FIFO,允許插入的一端稱為隊尾，允許刪除的一端稱為隊頭。 同樣是線性表，隊列也有類似線性表的各種操作，不同的就是插入數據只能在隊，尾進行，刪除數據只能在隊頭進行。 把隊列的這種頭尾相接的順序存儲結構稱為循環隊列。隊尾指針指向的位置永遠空出1位，所以隊列 最大容量比數組長度小1。 隊列的鏈式存儲結構，其實就是線性表的單鏈表，只不過它只能尾進頭出而已，我們把它簡稱為鏈隊列。 **雙端隊列:** 這種數據結構，可以說綜合了棧和隊列的優點，對雙端隊列來說，從隊頭一端可以入隊或出隊，從隊尾一端也可以入隊或出隊。盡管雙端隊列看起來似乎比棧和隊列更靈活，**但實際上在應用程序中遠不及棧和隊列有用。** **優先隊列**: ?優先隊列已經不屬于線性數據結構的范疇了，它是基于二叉堆來實現 ## hash 哈希 (散列表) 散列表也叫作哈希表 （hash table），這種數據結構提供了鍵（Key）和值（Value） 的映射關系。 底層使用數組, 通過哈希函數將 key 轉為 數組下標 當數據量大時， 容易出現哈希函數將不同的key 轉為數組下標時出現相同的值， 這就是**哈希沖突** 哈希沖突的解決： 開放尋址法：如果經過哈希函數獲得的下標所在位置已經有值，則往后移動一位，如果移動到的位置也已經有值了，就繼續往后移動，直到找到空位。開放尋址法有多種，這是最簡單的，java 的 ThreadLocal 就是這樣做的。 鏈表法（拉鏈法）：如果經過哈希函數獲得的下標所在位置已經有值，則在這個位置增加一個鏈表，這個位置所有的數據以key value 的對象形式都放到鏈表里，相當于數組嵌套鏈表。java的HashMap是這樣做的（1.8以后應該是紅黑樹） ### hash 的擴容 對于JDK中的散列表實現類HashMap來說，影響其擴容的因素有兩個。 Capacity ，即HashMap的當前長度 LoadFactor ，即HashMap的負載因子，默認值為0.75f HashMap.Size >= Capacity×LoadFactor **hash 擴容過程** 擴容 ，創建一個新的Entry空數組，長度是原數組的2倍。 重新Hash ，遍歷原Entry數組，把所有的Entry重新Hash到新數組中。為什么要重新Hash呢？因為長度擴大以后，Hash的規則也隨之改變。 經過擴容，原本擁擠的散列表重新變得稀疏，原有的Entry也重新得到了盡可能均勻的分配。 ## 樹 樹（tree）是n（n≥0）個節點的有限集。當n=0時，稱為空樹。在任意一 個非空樹中。 主要特點： 有且僅有一個特定的稱為根的節點。 當n>1時，其余節點可分為m（m>0）個互不相交的有限集，每一個集 合本身又是一個樹，并稱為根的子樹。 沒 有“孩子”的節點是葉子節點 樹的最大層級數，被稱為樹的高度或深度 ### 二叉樹 這種樹 的每個節點**最多有2個**孩子節點，也可能只 有1個，或者沒有孩子節點。 二叉樹節點的兩個孩子節點，一個被稱為左孩子（left child） ，一個被 稱為右孩子（right child） 。 二叉樹還有兩種特殊形式，一個叫作滿二叉樹 ，另一個叫作完 全二叉樹 。 **滿二叉樹：**一個二叉樹的所有非葉子節點都存在左右孩子，并且所有葉子節點都在 同一層級上，那么這個樹就是滿二叉樹。 滿二叉樹要求所有分支都是 滿的；而**完全二叉樹**只需保證**最后一個節點之前的節點都齊全**即可。 二叉樹可以用哪些物理存儲結構來表達呢？ 1. 鏈式存儲結構。 2. 數組。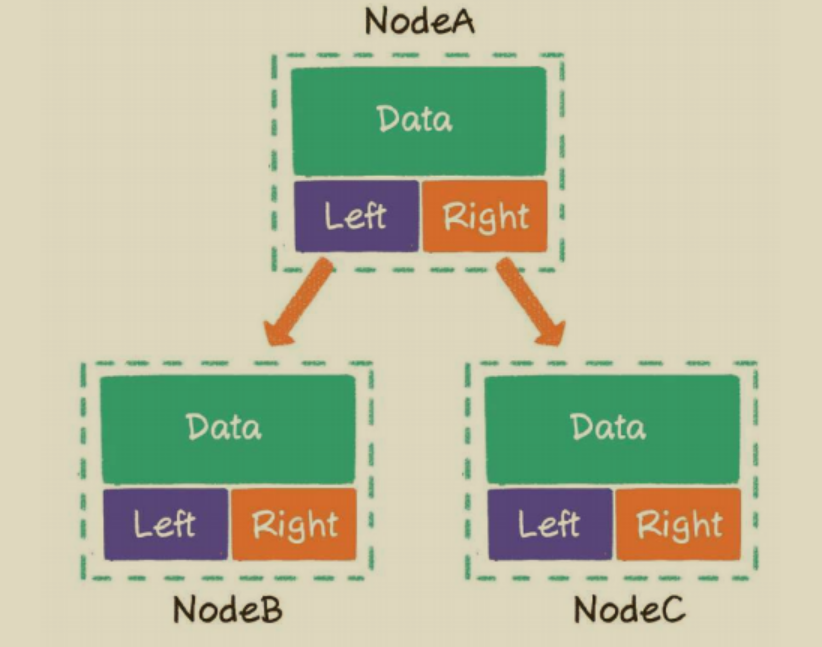  鏈表：一個節點最多可以指向左右兩個孩子節點，所 以二叉樹的每一個節點包含3部分。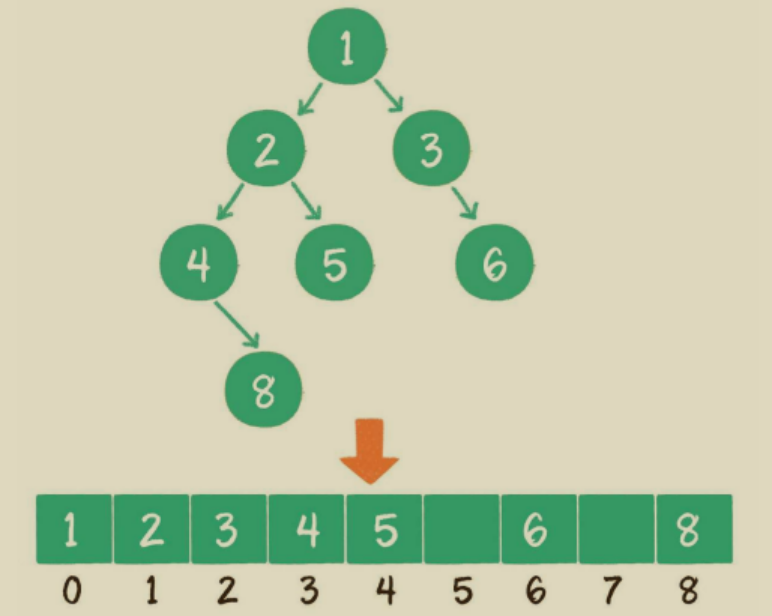 存儲數據的data變量 指向左孩子的left指針 指向右孩子的right指針  數組：按照層級順序把二叉樹的節點放到數組中對應的位 置上。如果某一個節點的左孩子或右孩子空缺，則數組的相應位置也空 出來 假設一個父節點的下標是parent，那么它的左孩子節點下標就 是2×parent + 1 ；右孩子節點下標就是2×parent + 2 。 反過來，假設一個左孩子節點的下標是leftChild，那么它的父節點下標 就是（leftChild-1）/ 2 。 ### 二叉查找樹（二叉排序樹） 二叉查找樹在二叉樹的基礎上增加了以下幾個條件。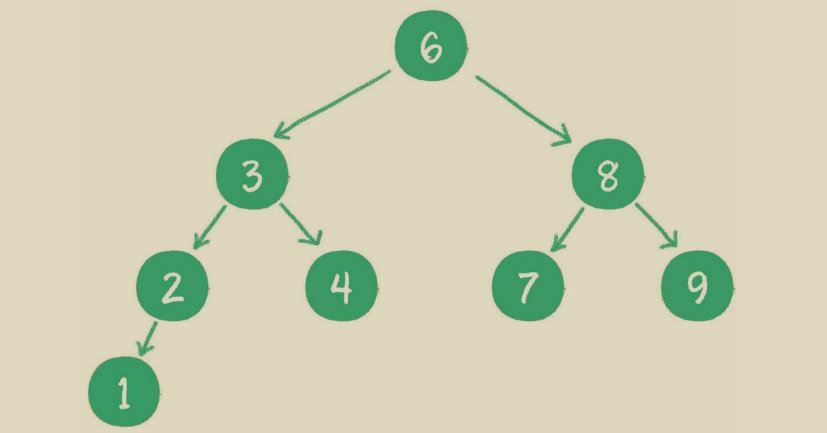 * 如果左子樹不為空，則左子樹上所有節點的值均小于根節點的值 * 如果右子樹不為空，則右子樹上所有節點的值均大于根節點的值 * 左、右子樹也都是二叉查找樹  二叉查找樹 利于查找和排序，但 9 8 7 6 5 等節點樹時會涉及二叉樹的自平衡，二叉樹自平衡的 方式有多種，如紅黑樹、AVL樹、樹堆等。 二叉樹的遍歷 1\. 深度優先遍歷 （前序遍歷、中序遍歷、后序遍歷）。 2\. 廣度優先遍歷 （層序遍歷）。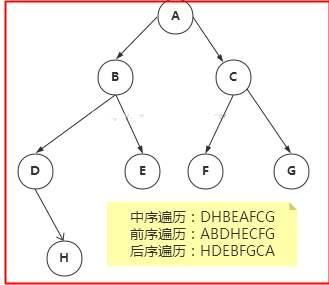 深度優先遍歷 二叉樹前序遍歷、中序遍歷、后序遍歷、層序遍歷的直觀理解 [https://blog.csdn.net/u013834525/article/details/80421684](https://blog.csdn.net/u013834525/article/details/80421684) （前序遍歷、中序遍歷、后序遍歷） 指的是 輸出根節點的順序  二叉樹的前序遍歷，輸出順序是根節點、左子樹、右子樹。 輸出順序 根 =》左 =》右 1\. 從樹的根節點開始輸出根節點，然后一直遍歷并輸出左子樹的左節點，直到節點沒有左子樹為止，這時候再去遍歷最后一個左節點的右子樹或者父節點的右子樹 2\. 遍歷右子樹時， 有左子樹的，再按照1的流程遍歷輸出這個右子樹。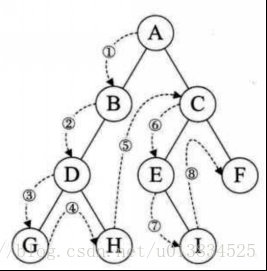  二叉樹的中序遍歷，輸出順序是左子樹、根節點、右子樹。 輸出順序 左 =》根 =》右 1\. 首先訪問根節點的左孩子，如果這個左孩子還擁有左孩子，則繼續深 入訪問下去，一直找到不再有左孩子的節點，并輸出該節點。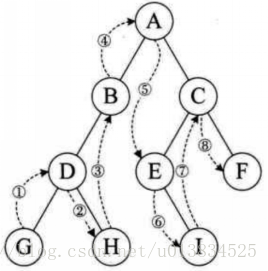  二叉樹的后序遍歷，輸出順序是根節點、左子樹、右子樹。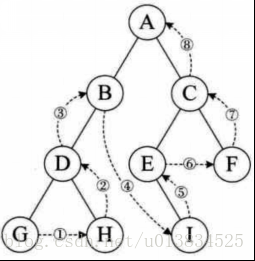 輸出順序 左 =》右 =》根  廣度優先遍歷 層序遍歷，顧名思義，就是二叉樹按照從根節點到葉子節點的層次關 系，一層一層橫向遍歷各個節點。代碼實現可以使用隊列  二叉堆 二叉堆本質上是一種完全二叉樹，它分為兩個類型。 1\. 最大堆。 最大堆的任何一個父節點的值，都大于或等于 它 左、右孩子節點的值。 2\. 最小堆。 最小堆的任何一個父節點的值，都小于或等于它左、 右孩子節點的值。 二叉堆的根節點叫作堆頂 。 最大堆的堆頂是整個堆中的最大元素 ；最小堆的堆頂是整個堆中的最小元素 。 堆的刪除操作是單一節點的“下沉”，這兩個操作的平均交換 次數都是堆高度的一半，所以時間復雜度是O(logn)。至于堆的構 建，需要所有非葉子節點依次“下沉”，所以我覺得時間復雜度應該 是O(n) 二叉堆雖然是一個完全二叉 樹，但它的存儲方式并不是鏈式存儲，而是順序存儲。換句話說，二叉 堆的所有節點都存儲在數組中。 假設父節點的下標是parent，那么它的左孩子下標就是 2×parent+1 ；右 孩子下標就是2×parent+2 。