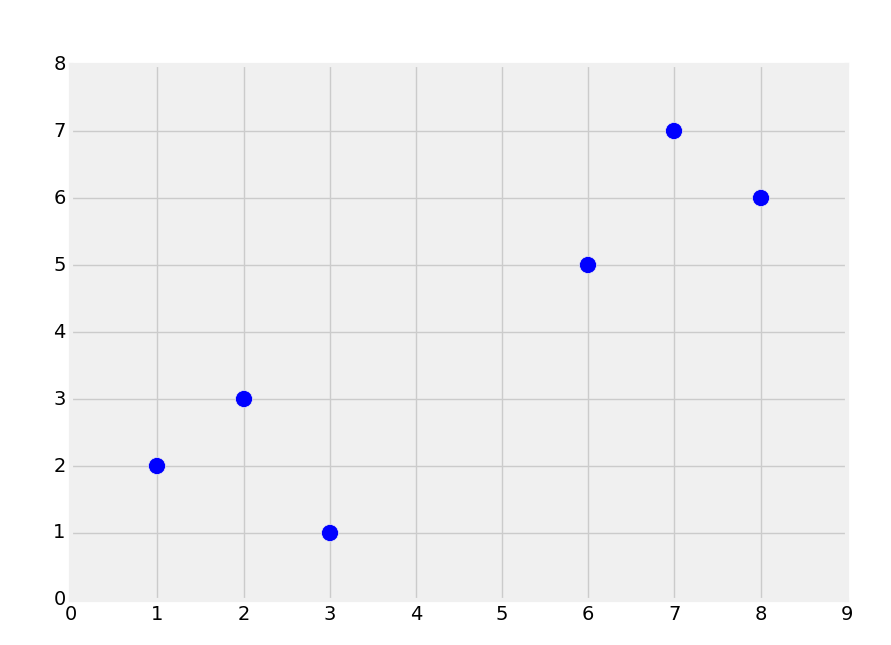
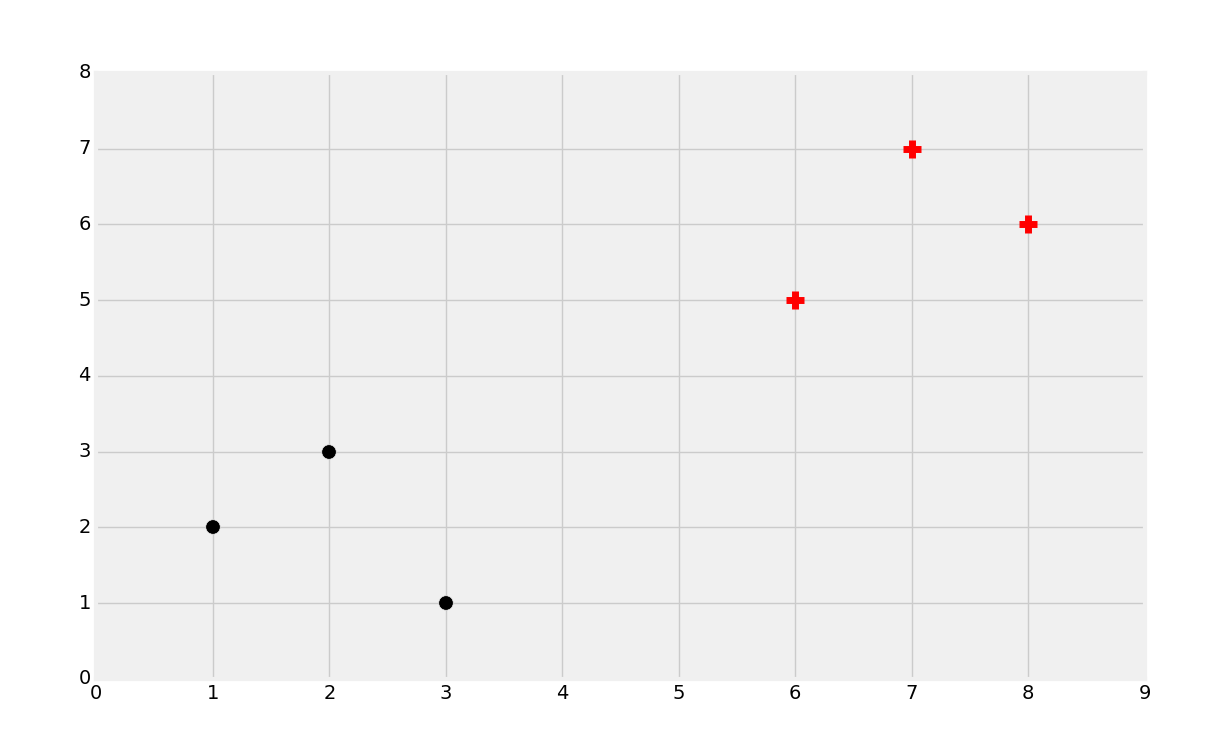
# 第二部分 分類 ## 十三、KNN 分類入門 歡迎閱讀第十三篇機器學習系列講義。我們開始了一個全新的部分：分類。這面，我們會涉及兩個主要的分類算法：K 最近鄰和支持向量機（SVM）。這兩個算法都是分類算法，它們的工作方式不同。 首先，讓我們考慮一個數據集，創建下面的圖像：  直觀上，你應該能夠看到兩個組。但是，分類是監督式機器學習。當我們將數據提供給機器學習算法的時候，我們實際上已經告訴它組的存在，以及哪個數據屬于哪個組。一個機器學習的相似形式是聚類，其中你讓機器尋找組，但它是非監督機器學習算法，后面我們會降到。所以，使用監督式機器學習，我們需要擁有預置標簽的數據用于訓練，像這樣：  這里我們擁有黑的點和紅的點。分類的目標就是拿已知的數據訓練機器，就像這樣，使機器能夠識別新數據的分類（紅的還是黑的）。例如，我們會處理乳腺腫瘤的數據，來基于一些屬性嘗試判斷是良性的還是惡性的。我們實現它的方式，就是獲取已知的樣本屬性，例如大小、形狀作為特征，標簽或者分類就是良性或者惡性。這里，我們可以根據縱六的相同屬性來評估未來的腫瘤，并且預測是良性還是惡性。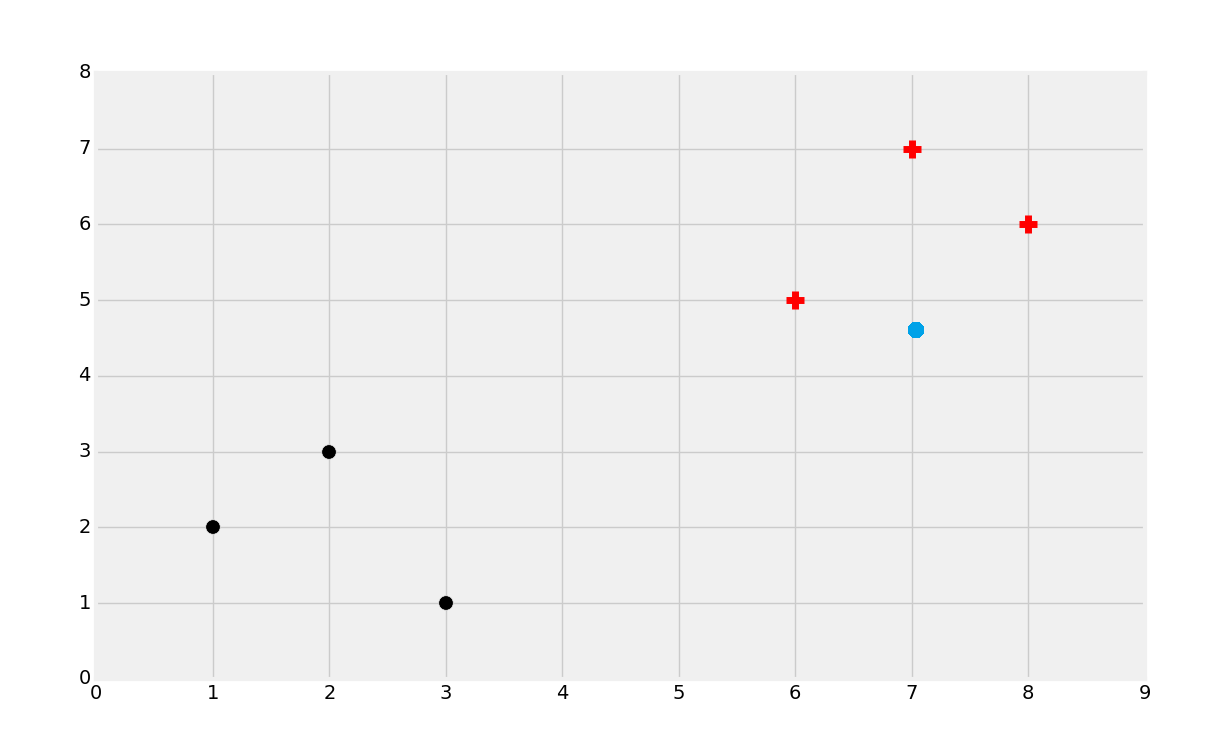 所以，分類的目標就是識別下面的點屬于哪個類：  你可能能猜到它是紅的類，但是為什么呢？嘗試為自己定義這里有什么參數。下面這種情況呢？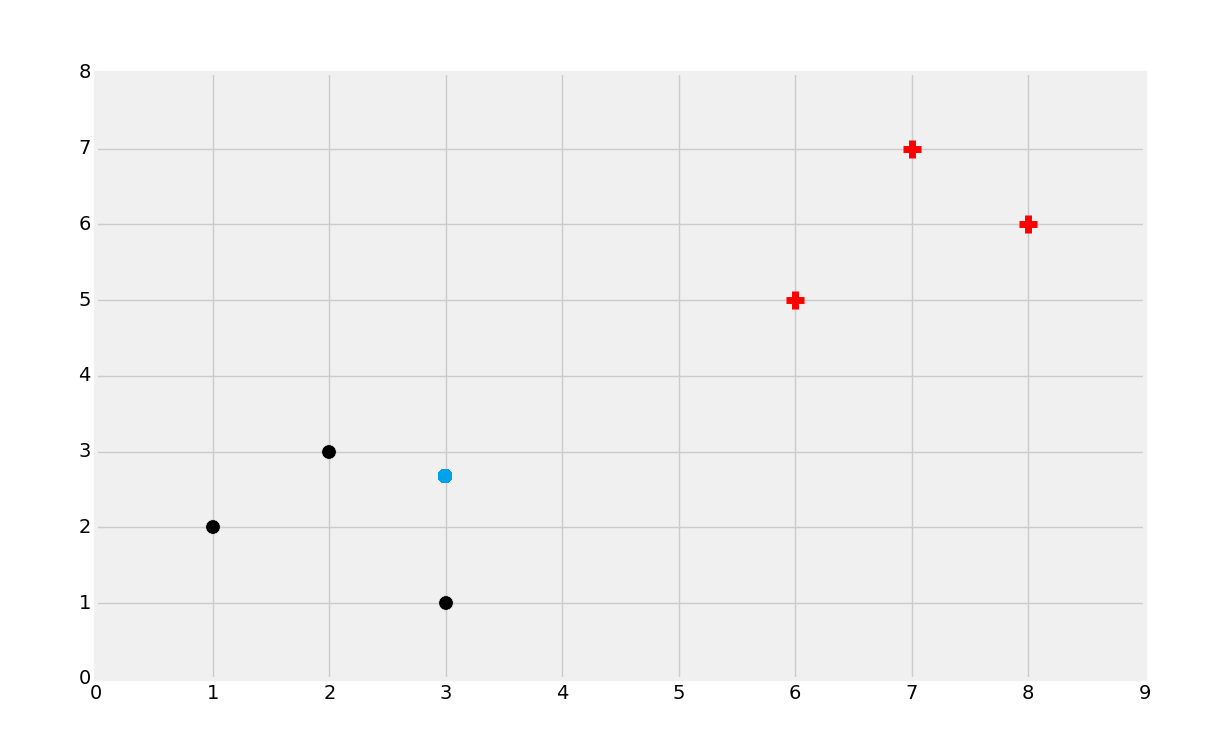  第二種情況中我們可能選取黑色。同樣，嘗試定義為啥這么選擇。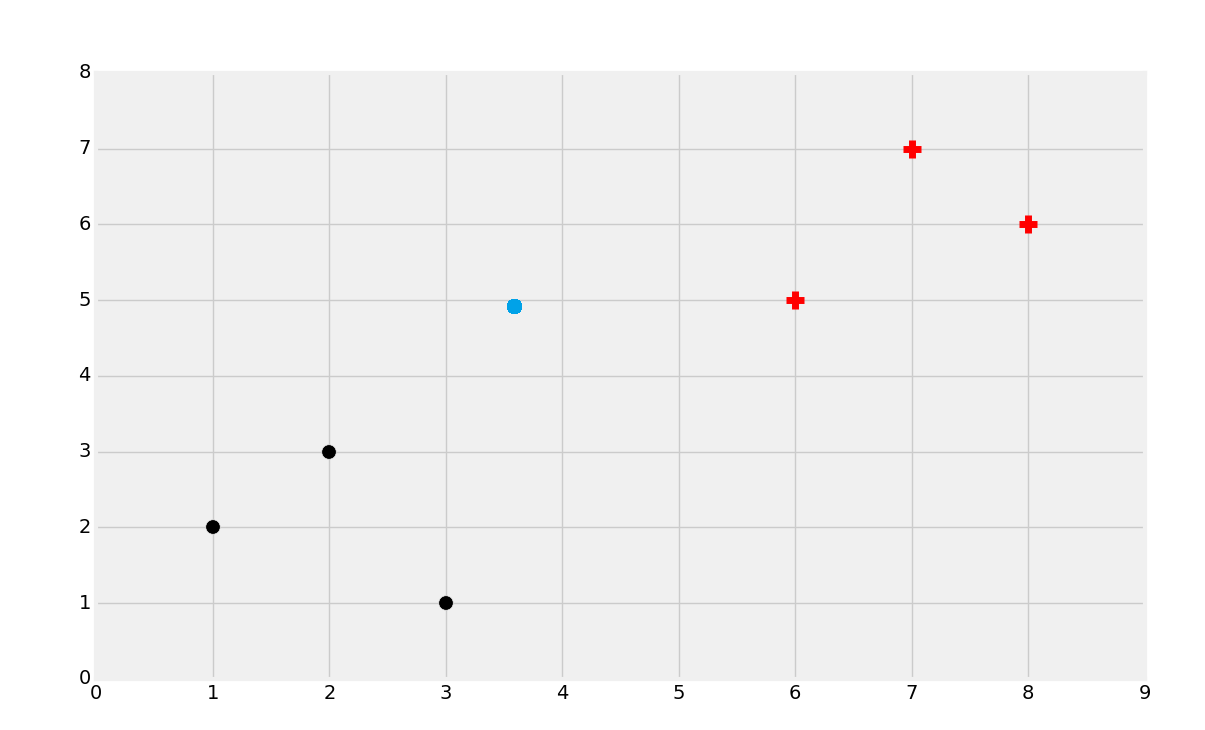最后，如果是這樣：  這種情況比較復雜，嘗試選取一種分類。 大多數人都會選擇黑色。無論哪種，考慮為什么你會做出這種選擇。多數人會根據近似性對數據集分組。直覺上它是最有意義的。如果你拿尺子畫出它到最近的黑色點的直線，之后畫出它到最近的紅色點的直線，你就會發現黑色點更近一些。與之相似，當數據點距離一個分組比另一個更近時，你就會基于近似性做出判斷。因此 KNN 機器學習算法就誕生了。 KNN 是個簡單高效的機器學習分類算法。如果這非常簡單，就像我們看到的那樣，我們為什么需要一個算法，而不是直接拿眼睛看呢？就像回歸那樣，機器可以計算得更快，處理更大的數據集，擴展，以及更重要的是，處理更多維度，例如 100 維。 它的工作方式就是它的名字。K 就是你選取的數量，近鄰就是已知數據中的相鄰數據點。我們尋找任意數量的“最近”的相鄰點。假設`K=3`，所以我們就尋找三個最近的相鄰點。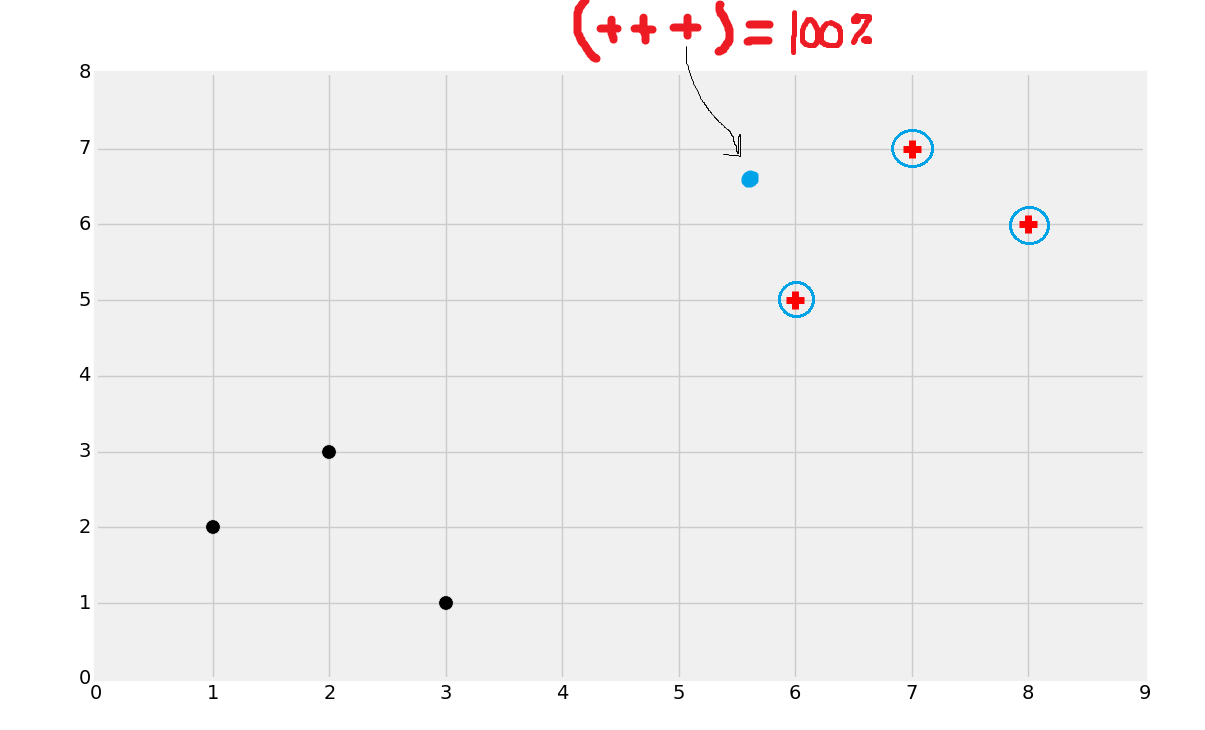例如：  上面的圖中，我圈出了三個最近的相鄰點。這里，所有三個點都是紅色分類。KNN 會基于相鄰點進行計數。所有三個近鄰都是紅色，所以它 100% 是紅色分類。如果兩個近鄰都是紅色，一個是黑色，我們也將其分類為紅色，只是置信度就少了。要注意，由于計數的本質，你會更希望使用奇數 K，否則會產生 50:50 的情況。有一種方式在距離上應用權重，來懲罰那些更遠的點，所以你就可以使用偶數的 K 值了。 下一個教程中，我們會涉及到 Scikit 的 KNN 算法，來處理乳腺腫瘤數據，之后我們會嘗試自己來編寫這個算法。 ## 十四、對數據使用 KNN 歡迎閱讀第十四個部分。上一個部分我們介紹了分類，它是一種機器學習的監督算法，并且解釋了 KNN 算法的直覺。這個教程中，我們打算使用 Sklearn，講解一個簡單的算法示例，之后在后面的教程中，我們會構建我們自己的算法來更多了解背后的工作原理。 為了使用例子說明分類，我們打算使用[乳腺腫瘤數據集](https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+%28Original%29)，它是 UCI 所貢獻的數據集，從威斯康星大學收集。UCI 擁有龐大的[機器學習倉庫](https://archive.ics.uci.edu/ml/datasets.html)。這里的數據集組織為經常使用的機器學習算法類型、數據類型、屬性類型、主題范圍以及其它。它們對教學和機器學習算法開發都很實用。我自己經常瀏覽那里，非常值得收藏。在乳腺腫瘤數據集的頁面，選擇[`Data Folder`鏈接](https://archive.ics.uci.edu/ml/machine-learning-databases/breast-cancer-wisconsin/)。之后，下載`breast-cancer-wisconsin.data`和`breast-cancer-wisconsin.names`。這些可能不能下載，而是會在瀏覽器中展示。如果是這樣右鍵點擊“另存為”。 下載之后，打開`breast-cancer-wisconsin.names`文件。查看文件，向下滾動 100 行，我們就能獲取屬性（列）的名稱、使用這些信息，我們打算手動將這些標簽添加到` breast-cancer-wisconsin.data`文件中。打開它，并輸入新的第一行： ``` id,clump_thickness,uniform_cell_size, uniform_cell_shape,marginal_adhesion, single_epi_cell_size,bare_nuclei,bland_chromation, normal_nucleoli,mitoses,class ``` 之后，你應該會思考，我們的特征和標簽應該是什么。我們嘗試對數據進行分類，所以很顯然分類就是這些屬性會導致良性還是惡性。同樣，大多數這些屬性看起來都是可用的，但是是否有任何屬性與其它屬性類似，或者是無用的？ID 屬性并不是我們打算扔給分類器的東西。 缺失或者損壞的數據：這個數據集擁有一些缺失數據，我們需要清理。讓我們以導入來開始，拉取數據，之后做一些清理： ```py import numpy as np from sklearn import preprocessing, cross_validation, neighbors import pandas as pd df = pd.read_csv('breast-cancer-wisconsin.data.txt') df.replace('?',-99999, inplace=True) df.drop(['id'], 1, inplace=True) ``` 在讀取數據之后，我們注意到，有一些列存在缺失數據。這些缺失數據以`?`填充。`.names`文件告訴了我們，但是我們最終可以通過錯誤來發現，如果我們嘗試將這些信息扔給分類為。這個時候，我們選擇將缺失數據填充為 -99999 值。你可以選擇你自己的方法來處理缺失數據，但是在真實世界中，你可能發現 50% 或者更多記錄，一個或多個列都含有缺失數據。尤其是，如果你使用可擴展的屬性來收集數據。-99999 并不完美，但是它足夠有效了。下面，我們丟棄了 ID 列。完成之后，我們會注釋掉 ID 列的丟棄，只是看看包含他可能有哪些影響。 下面，我們定義我們的特征和標簽。 特征`X`是除了分類的任何東西。調用`df.drop`會返回一個新的 DataFrame，不帶丟棄的列。標簽`y`僅僅是分類列。 現在我們創建訓練和測試樣本，使用 Sklearn 的`cross_validation.train_test_split`。 ```py X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size=0.2) ``` 定義分類器： ```py clf = neighbors.KNeighborsClassifier() ``` 這里，我們使用 KNN 分類器。 訓練分類器： ```py clf.fit(X_train, y_train) ``` 測試： ```py accuracy = clf.score(X_test, y_test) print(accuracy) ``` 結果應該是 95%，并且開箱即用，無需任何調整。非常棒。讓我們展示一下，當我們注釋掉 ID 列，包含一些無意義和誤導性的數據之后，會發生什么。 ```py import numpy as np from sklearn import preprocessing, cross_validation, neighbors import pandas as pd df = pd.read_csv('breast-cancer-wisconsin.data.txt') df.replace('?',-99999, inplace=True) #df.drop(['id'], 1, inplace=True) X = np.array(df.drop(['class'], 1)) y = np.array(df['class']) X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size=0.2) clf = neighbors.KNeighborsClassifier() clf.fit(X_train, y_train) accuracy = clf.score(X_test, y_test) print(accuracy) ``` 影響很令人吃驚，準確率從 95% 降到了 60%。在未來，如果 AI 通知了這個星球，要注意你只需要給它一些無意義的屬性來智取它。非常有意思，添加噪聲是一種損害你的算法的方式。當你和你的機器人霸主較量時，分辨有意義和惡意的噪聲會節省你的時間。 下面你可以大致猜測，我們如何做預測，如果你遵循了 Sklearn 的教程。首先，我們需要一些沿革本數據。我們可以自己編。例如，我們會查看樣本文件的某一行。你可以添加噪聲來執行進一步的分析，假設標準差不是那么離譜。這么做也比較安全，由于你并不在篡改的數據上訓練，你僅僅做了測試。我會通過編造一行來手動實現它。 ```py example_measures = np.array([4,2,1,1,1,2,3,2,1]) ``` 你可以盡管在文檔中搜索特征列表。它不存在。現在你可以： ```py prediction = clf.predict(example_measures) print(prediction) ``` 或者取決于你的閱讀時間，你可能不能這么做。在這么做的時候，我得到了一個警告： ```py DeprecationWarning: Passing 1d arrays as data is deprecated in 0.17 and will raise ValueError in 0.19. Reshape your data either using X.reshape(-1, 1) if your data has a single feature or X.reshape(1, -1) if it contains a single sample. ``` 好的，沒有問題。我們只擁有一個特征嗎？不是。我們只擁有一個記錄嗎？是的。所以我們使用`X.reshape(1, -1)`。 ```py example_measures = np.array([4,2,1,1,1,2,3,2,1]) example_measures = example_measures.reshape(1, -1) prediction = clf.predict(example_measures) print(prediction) # 0.95 # [2] ``` 這里的第一個輸出是準確率（95%）和預測（2）。這就是我們的偽造數據的建模。 如果我們有兩條呢？ ```py example_measures = np.array([[4,2,1,1,1,2,3,2,1],[4,2,1,1,1,2,3,2,1]]) example_measures = example_measures.reshape(2, -1) prediction = clf.predict(example_measures) print(prediction) ``` 忽略這個硬編碼。如果我們不知道有幾何樣例會怎么樣？ ```py example_measures = np.array([[4,2,1,1,1,2,3,2,1],[4,2,1,1,1,2,3,2,1]]) example_measures = example_measures.reshape(len(example_measures), -1) prediction = clf.predict(example_measures) print(prediction) ``` 你可以看到，KNN 算法的實現不僅僅很簡單，而且這里也很準確。下一個教程中，我們打算從零構建我們自己的 KNN 算法，而不是使用 Sklearn，來嘗試了解更多算法的東西，理解它的工作原理，最重要的是，了解它的陷阱。 ## 十五、對數據使用 KNN 歡迎閱讀第十五篇教程，其中我們當前涉及到使用 KNN 算法來分類。上一篇教程中，我們涉及到如何使用 Sklearn 的 KNN 算法來預測良性或者惡性腫瘤，基于腫瘤的屬性，準確率有 95%。現在，我們打算深入 KNN 的工作原理，以便完全理解算法本身，來使其更好為我們工作。 我們會回到我們的乳腺腫瘤數據集，對其使用我們自定義 KNN 算法，并將其與 Sklearn 的比較，但是我們打算首先以一個非常簡單的理論開始。KNN 基于近似性，不是分組，而是單獨的點。所以，所有這種算法所做的，實際上是計算點之間的距離，并且之后選取距離最近的前 K 個點的最常出現的分類。有幾種方式來計算平面上的距離，他們中許多都可以在這里使用，但是最常使用的版本是歐氏距離，以歐幾里得命名。他是一個著名的數學家，被稱為幾何之父，他編寫了《幾何原本》，被稱為數學家的圣經。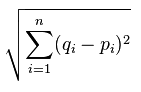歐氏距離為：  所以這是什么意思？基本上，它是每個點之間距離的平方和的平方根。在 Python 的術語中，是這樣： ```py plot1 = [1,3] plot2 = [2,5] euclidean_distance = sqrt( (plot1[0]-plot2[0])**2 + (plot1[1]-plot2[1])**2 ) ``` 這里距離是 2.236。 這就是 KNN 背后的基本數學原理了，現在我們僅僅需要構建一個系統來處理算法的剩余部分，例如尋找最近距離，它們的分組，然后是計數。 ## 十六、從零創建 KNN 分類器：第一部分 歡迎閱讀第十六個部分，我們現在涉及到 KNN 算法的分類。在上一個教程中，我們涉及到了歐氏距離，現在我們開始使用純粹的 Python 代碼來建立我們自己的簡單樣例。 最開始，讓我們導入下列東西并為 Matplotlib 設置一個樣式。 ```py import numpy as np import matplotlib.pyplot as plt from matplotlib import style import warnings from math import sqrt from collections import Counter style.use('fivethirtyeight') ``` 我們打算使用警告來避免使用比分組數量更低的 K 值，至少是最開始（因為我會展示一個更加高效的方法），之后對集合計數來獲取出現次數最多的分類。 下面，我們創建一些數據： ```py dataset = {'k':[[1,2],[2,3],[3,1]], 'r':[[6,5],[7,7],[8,6]]} new_features = [5,7] ``` 這個數據集只是個 Python 字典，鍵是點的顏色（將這些看做分類），值是屬于這個分類的數據點。如果你回憶我們的乳腺腫瘤數據集，分類都是數字，通常 Sklearn 只能處理數字。例如，向量翻譯為任意數字`2`，而惡性翻譯為任意數字`4`，而不是一個字符串。這是因為，Sklearn 只能使用數字，但是你并不一定要使用數字來代表分類。下面，我們創建簡單的數據集`5, 7`，用于測試。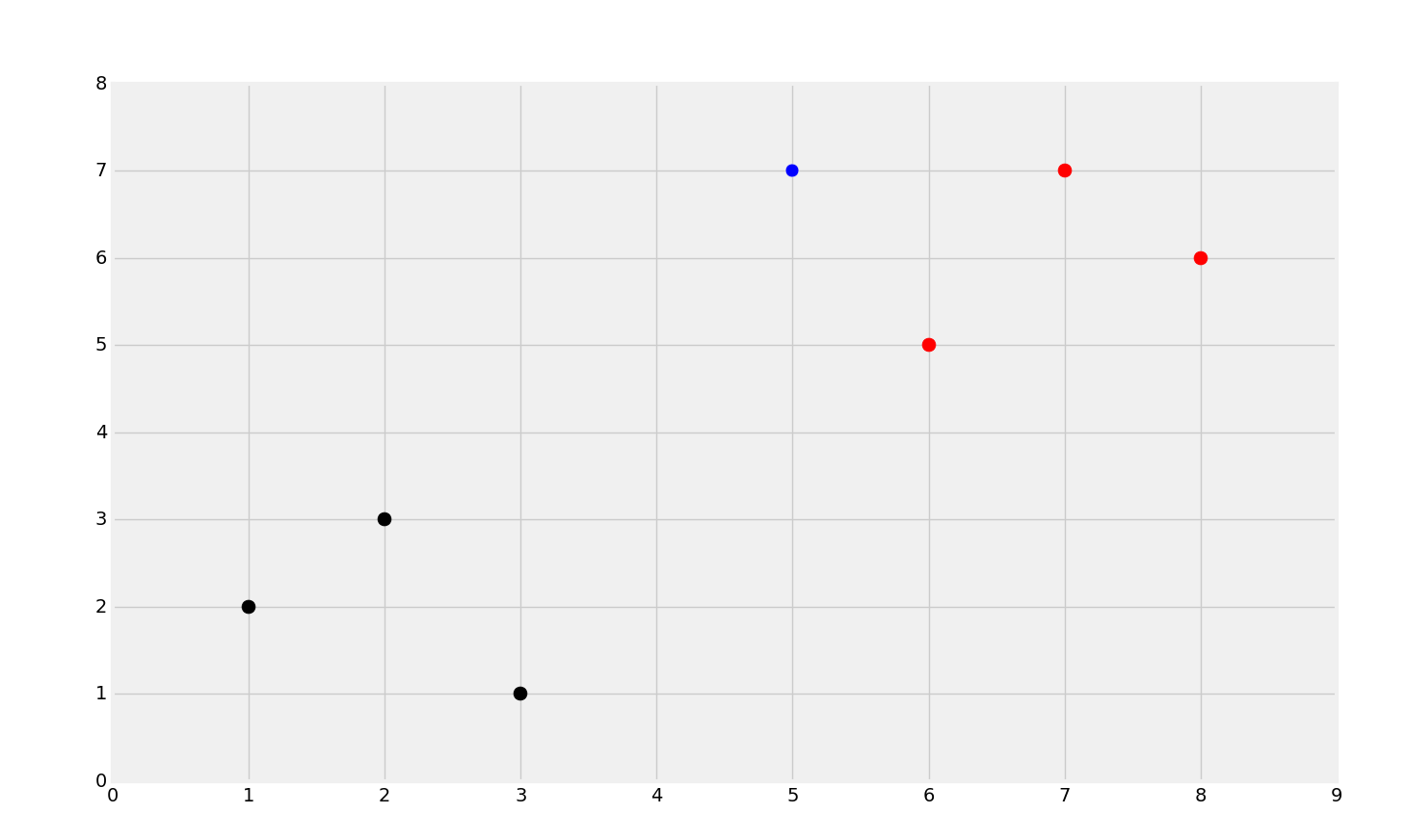我們可以這樣來快速繪圖： ```py [[plt.scatter(ii[0],ii[1],s=100,color=i) for ii in dataset[i]] for i in dataset] plt.scatter(new_features[0], new_features[1], s=100) plt.show() ```  ` [[plt.scatter(ii[0],ii[1],s=100,color=i) for ii in dataset[i]] for i in dataset]`這一行和下面這個相同： ```py for i in dataset: for ii in dataset[i]: plt.scatter(ii[0],ii[1],s=100,color=i) ``` 你可以看到紅色和黑色的明顯分組，并且我們還有藍色的點，它是`new_features`，我們打算對其分類。 我們擁有了數據，現在我們打算創建一些函數，來分類數據。 ```py def k_nearest_neighbors(data, predict, k=3): return vote_result ``` 這就是我們的框架，從這里開始。我們想要一個函數，它接受要訓練的數據，預測的數據，和 K 值，它的默認值為 3。 下面，我們會開始填充函數，首先是一個簡單的警告： ```py def k_nearest_neighbors(data, predict, k=3): if len(data) >= k: warnings.warn('K is set to a value less than total voting groups!') return vote_result ``` 如果選取的最近鄰的數量小于或等于分類數量，那么就給出警告（因為這樣會產生偏差）。 現在，如何尋找最近的三個點呢？是否有一些用于搜索的魔法呢？沒有，如果有的話，也是很復雜而。為什么呢？KNN 的工作原理是，我們需要將問題中的數據與之前的數據比較，之后才能知道最近的點是什么。因此，如果你的數據越多，KNN 就越慢。我們這里告一段落，但是要考慮是否有方法來加速這個過程。 ## 十七、從零創建 KNN 分類器：第二部分 歡迎閱讀第十七個部分，我們正在講解 KNN 算法的分類。上一個教程中，我們開始構建我們的 KNN 示例，這里我們將其完成。 我處理它的方式，就是首先創建一個 Python 列表，它包含另一個列表，里面包含數據集中每個點的距離和分類。一旦填充完畢，我們就可以根據距離來排序列表，截取列表的前 K 個值，找到出現次數最多的，就找到了答案。 ```py def k_nearest_neighbors(data, predict, k=3): if len(data) >= k: warnings.warn('K is set to a value less than total voting groups!') distances = [] for group in data: for features in data[group]: euclidean_distance = sqrt( (features[0]-predict[0])**2 + (features[1]-predict[1])**2 ) distances.append([euclidean_distance,group]) ``` 有一種方式來計算歐氏距離，最簡潔的方式就是遵循定義。也就是說，使用 NumPy 會更快一點。由于 KNN 是一種機器學習的爆破方法，我們需要我們能得到的所有幫助。因此，我們可以將函數修改一點。一個選項是： ```py euclidean_distance = np.sqrt(np.sum((np.array(features)-np.array(predict))**2)) print(euclidean_distance) ``` 這還是很清楚，我們剛剛使用了 NumPy 版本。NumPy 使用 C 優化，是個非常高效的庫，很多時候允許我們計算更快的算術。也就是說，NumPy 實際上擁有大量的線性代數函數。例如，這是范數： ```py euclidean_distance = np.linalg.norm(np.array(features)-np.array(predict)) print(euclidean_distance) ``` 歐式距離度量兩個端點之間的線段長度。歐幾里得范數度量向量的模。向量的模就是它的長度，這個是等價的。名稱僅僅告訴你你所在的控件。 我打算使用后面那一個，但是我會遵循我的約定，使其易于拆解成代碼。如果你不了解 NumPy 的內建功能，你需要去了解如何使用。 現在，`for`循環之外，我們得到了距離列表，它包含距離和分類的列表。我們打算對列表排序，之后截取前 K 個元素，選取下標 1，它就是分類。 ```py votes = [i[1] for i in sorted(distances)[:k]] ``` 上面，我們遍歷了排序后的距離列表的每個列表。排序方法會（首先）基于列表中每個列表的第一個元素。第一個元素是距離，所以執行`orted(distances)`之后我們就按照從小到大的距離排序了列表。之后我們截取了列表的`[:k]`，因為我們僅僅對前 K 個感興趣。最后，在`for`循環的外層，我們選取了`i[1]`，其中`i`就是列表中的列表，它包含`[diatance, class]`（距離和分類的列表）。按照距離排序之后，我們無需再關心距離，只需要關心分類。 所以現在有三個候選分類了。我們需要尋找出現次數最多的分類。我們會使用 Python 標準庫模塊`collections.Counter`。 ```py vote_result = Counter(votes).most_common(1)[0][0] ``` `Collections`會尋找最常出現的元素。這里，我們想要一個最常出現的元素，但是你可以尋找前 3 個或者前`x`個。如果沒有`[0][0]`這部分，你會得到`[('r', 3)]`（元素和計數的元組的列表）。所以`[0][0]`會給我們元組的第一個元素。你看到的 3 是`'r'`的計數。 最后，返回預測結果，就完成了。完整的代碼是： ```py def k_nearest_neighbors(data, predict, k=3): if len(data) >= k: warnings.warn('K is set to a value less than total voting groups!') distances = [] for group in data: for features in data[group]: euclidean_distance = np.linalg.norm(np.array(features)-np.array(predict)) distances.append([euclidean_distance,group]) votes = [i[1] for i in sorted(distances)[:k]] vote_result = Counter(votes).most_common(1)[0][0] return vote_result ``` 現在，如果我們打算基于我們之前所選的點，來做預測： ```py result = k_nearest_neighbors(dataset, new_features) print(result) ``` 非常肯定，我得到了`r`，這就是預期的值。讓我們繪制它吧。 ```py import numpy as np import matplotlib.pyplot as plt from matplotlib import style import warnings from math import sqrt from collections import Counter style.use('fivethirtyeight') def k_nearest_neighbors(data, predict, k=3): if len(data) >= k: warnings.warn('K is set to a value less than total voting groups!') distances = [] for group in data: for features in data[group]: euclidean_distance = np.linalg.norm(np.array(features)-np.array(predict)) distances.append([euclidean_distance,group]) votes = [i[1] for i in sorted(distances)[:k]] vote_result = Counter(votes).most_common(1)[0][0] return vote_result dataset = {'k':[[1,2],[2,3],[3,1]], 'r':[[6,5],[7,7],[8,6]]} new_features = [5,7] [[plt.scatter(ii[0],ii[1],s=100,color=i) for ii in dataset[i]] for i in dataset] # same as: ##for i in dataset: ## for ii in dataset[i]: ## plt.scatter(ii[0],ii[1],s=100,color=i) plt.scatter(new_features[0], new_features[1], s=100) result = k_nearest_neighbors(dataset, new_features) plt.scatter(new_features[0], new_features[1], s=100, color = result) plt.show() ```  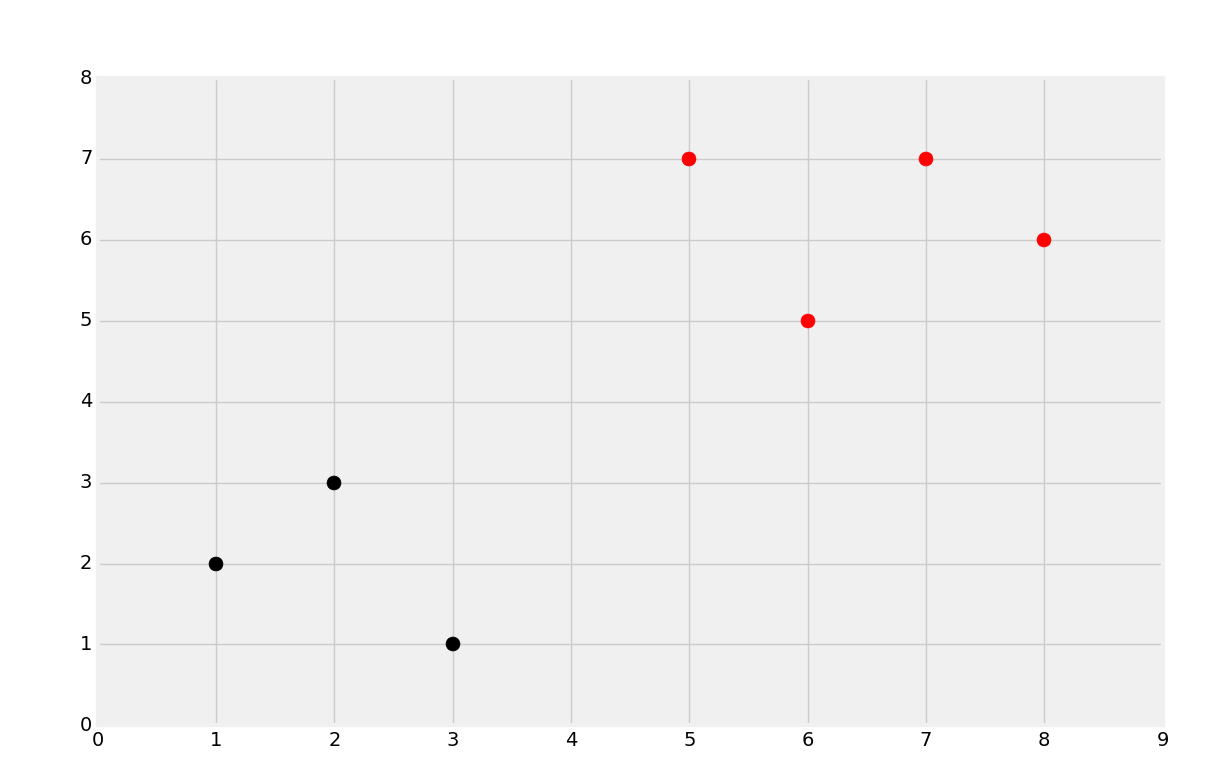你可以看到，我們添加了新的點`5, 7`，它分類為紅色的點，符合預期。 這只是小規模的處理，但是如果我們處理乳腺腫瘤數據集呢？我們如何和 Sklearn 的 KNN 算法比較？下一個教程中，我們會將算法用于這個數據集。 ## 十八、測試 KNN 分類器 歡迎閱讀第十八篇教程，我們剛剛編寫了我們自己的 KNN 分類器算法，現在我們準備好了使用一些真實數據來測試它。開始，我們打算使用之前的乳腺腫瘤數據集。如果你沒有它，返回教程 13 并抓取數據。 目前為止，我們的算法像這樣處理數據：  其中藍色的點是位置數據，運行算法，并正確分類數據：  現在，我們打算回顧乳腺腫瘤數據集，它記錄腫瘤的屬性變將它們按照良性還是惡性分類。Sklearn 的 KNN 分類器有 95% 的準確率，并且我們打算測試我們自己的算法。 我們會以下列代碼開始： ```py import numpy as np import warnings from collections import Counter import pandas as pd import random def k_nearest_neighbors(data, predict, k=3): if len(data) >= k: warnings.warn('K is set to a value less than total voting groups!') distances = [] for group in data: for features in data[group]: euclidean_distance = np.linalg.norm(np.array(features)-np.array(predict)) distances.append([euclidean_distance,group]) votes = [i[1] for i in sorted(distances)[:k]] vote_result = Counter(votes).most_common(1)[0][0] return vote_result ``` 這應該看起來很熟悉。要注意我導入了 Pandas 和 random。我已經移除了 Matplotlib 的導入，因為我們不打算繪制任何東西。下面，我們打算加載數據： ```py df = pd.read_csv('breast-cancer-wisconsin.data.txt') df.replace('?',-99999, inplace=True) df.drop(['id'], 1, inplace=True) full_data = df.astype(float).values.tolist() ``` 這里，我們加載了數據，替換掉了問號，丟棄了 ID 列，并且將數據轉危為列表的列表。要注意我們顯式將 DataFrame 轉換為浮點類型。出于一些原因，至少對于我來說，一些數據點仍然是數字，但是字符串數據類型并不是很好。 下面，我們打算把數據打亂，之后將其分割： ```py Next, we're going to shuffle the data, and then split it up: random.shuffle(full_data) test_size = 0.2 train_set = {2:[], 4:[]} test_set = {2:[], 4:[]} train_data = full_data[:-int(test_size*len(full_data))] test_data = full_data[-int(test_size*len(full_data)):] ``` 首先我們打亂了數據（它包含特征和標簽）。之后我們為訓練和測試集準備了一個字典用于填充。下面，我們指定了哪個是`train_data `，哪個是`test_data`。我們選取前 80% 作為`train_data `（邏輯是在后 20% 的地方分割），之后我們通過在后 20% 的地方分割，來創建`test_data`。 現在我們開始填充字典。如果不清楚的話，字典有兩個鍵：2 和 4。2 是良性腫瘤（和實際數據集相同），4 是惡性腫瘤，也和數據集相同。我們將其硬編碼，但是其他人可以選取分類，并像這樣創建字典，它的鍵是分類中的唯一值。我們僅僅是使其簡單。 ```py for i in train_data: train_set[i[-1]].append(i[:-1]) for i in test_data: test_set[i[-1]].append(i[:-1]) ``` 現在我們填充了字典，我們擁有了測試集，其中鍵是分類，值是屬性。 最后就是訓練和測試的時候了。使用 KNN，這些步驟基本就完成了，因為訓練步驟就是把點村進內存，測試步驟就是比較距離： ```py correct = 0 total = 0 for group in test_set: for data in test_set[group]: vote = k_nearest_neighbors(train_set, data, k=5) if group == vote: correct += 1 total += 1 print('Accuracy:', correct/total) ``` 現在我們首先迭代測試集的分組（分類，2 或者 4，也是字典的鍵），之后我們遍歷每個數據點，將數據點扔給`k_nearest_neighbors`，以及我們的訓練集`train_set`，之后是我們的 K，它是 5。我選擇了 5，純粹是因為它是 SKlearn 的`KNeighborsClassifier`的默認值。所以我們的完整代碼是： ```py import numpy as np import matplotlib.pyplot as plt from matplotlib import style import warnings from collections import Counter #dont forget this import pandas as pd import random style.use('fivethirtyeight') def k_nearest_neighbors(data, predict, k=3): if len(data) >= k: warnings.warn('K is set to a value less than total voting groups!') distances = [] for group in data: for features in data[group]: euclidean_distance = np.linalg.norm(np.array(features)-np.array(predict)) distances.append([euclidean_distance,group]) votes = [i[1] for i in sorted(distances)[:k]] vote_result = Counter(votes).most_common(1)[0][0] return vote_result df = pd.read_csv('breast-cancer-wisconsin.data.txt') df.replace('?',-99999, inplace=True) df.drop(['id'], 1, inplace=True) full_data = df.astype(float).values.tolist() random.shuffle(full_data) test_size = 0.2 train_set = {2:[], 4:[]} test_set = {2:[], 4:[]} train_data = full_data[:-int(test_size*len(full_data))] test_data = full_data[-int(test_size*len(full_data)):] for i in train_data: train_set[i[-1]].append(i[:-1]) for i in test_data: test_set[i[-1]].append(i[:-1]) correct = 0 total = 0 for group in test_set: for data in test_set[group]: vote = k_nearest_neighbors(train_set, data, k=5) if group == vote: correct += 1 total += 1 print('Accuracy:', correct/total) ``` ## 十九、KNN 的最終見解 既然我們了解了它的工作原理，這里我們打算涉及一些 KNN 算法的最終見解，包含 K 值，置信度，速度，以及算法的優點和缺點。 在執行 100 個樣例的測試之后，Sklearn 的`neighbors.KNeighborsClassifier`分類器的準確率是 0.97，我們自己編寫的分類器也一樣。不要故步自封，因為這個算法非常簡單和基礎。KNN 分類器的真正價值并不在準確率上，而是它的速度。KNN 分類器的主要缺陷就是就是速度，你可以用它來執行操作。 對于速度，Sklearn 的 KNN 版本的每個周期是 0.044 秒，我們的是 0.55 秒。因此，雖然我們實現了相同的結果，我們比 Sklearn 慢很多。好的消息是，如果你對它們如何實現的感興趣，你可以查看源代碼、我們也提到了，我們也可以使用一個主流方式來提升速度。KNN 并不需要過多的訓練。訓練僅僅是將數據集加載到內存。你可以將數據集保留在內存中，但是 KNN 分類器的真正痛點就是對比每個數據集來尋找最近的那個。之后，如果你打算對 1000 個數據集分類，會發生什么呢？是的，一個選項是可以并發。串行執行它們沒有任何好處。我們的方式是這樣，僅僅使用一點點的處理器的能力。但是，我們可以一次性至少計算 100~200 個數據，即使是在便宜的處理器上。如果你打算了解如何并發，看一看這個[并發教程](https://pythonprogramming.net/threading-tutorial-python/)。使用 Sklearn，KNN 分類器自帶一個并行處理參數`n_jobs`。你可以將其設置為任何數值，你可以以這個線程數來并發。如果你打算一次運行 100 個操作，`n_jobs=100`。如果你僅僅打算運行盡可能做的操作，設置`n_jobs=-1`。閱讀[最近鄰文檔](https://scikit-learn.org/stable/modules/generated/sklearn.neighbors.NearestNeighbors.html#sklearn.neighbors.NearestNeighbors)，你可以了解更多選項。有幾種方式將你的數據與指定半徑之內的數據對比，如果你對加速 KNN，以及 Sklearn 的 KNN 版本感興趣，你可能想要看一看。 最后，我要講的最后一點就是預測的置信度。有兩種方式來度量置信度。一種是比較你預測對了多少個點，另一個是，檢查計數的百分比。例如，你的算法準確率可能是 97%，但是對于一些分類，計數可能是 3 比 2。其中 3 是主流，它的占有率是 60%，而不是理想情況下的 100%。但是告訴別人它是否有癌癥的話，就像自動駕駛汽車分辨一團土和毛毯上的孩子，你可能更希望是 100%。可能 60% 的計數就是 3% 的不準確度量的一部分。 好的，所以我們剛剛編寫了準確率為 97% 的分類器，但是沒有把所有事情都做好。KNN 非常擁有，因為它對線性和非線性數據都表現出色。主要的缺陷是規模、離群點和不良數據（要記得 ID 列的無效引入）。 我們仍然專注于監督式機器學習，特別是分類，我們下面打算設計支持向量機。 最后的代碼： ```py import numpy as np from math import sqrt import warnings from collections import Counter import pandas as pd import random def k_nearest_neighbors(data, predict, k=3): if len(data) >= k: warnings.warn('K is set to a value less than total voting groups!') distances = [] for group in data: for features in data[group]: euclidean_distance = np.linalg.norm(np.array(features)-np.array(predict)) distances.append([euclidean_distance, group]) votes = [i[1] for i in sorted(distances)[:k]] vote_result = Counter(votes).most_common(1)[0][0] confidence = Counter(votes).most_common(1)[0][1] / k return vote_result, confidence df = pd.read_csv("breast-cancer-wisconsin.data.txt") df.replace('?',-99999, inplace=True) df.drop(['id'], 1, inplace=True) full_data = df.astype(float).values.tolist() random.shuffle(full_data) test_size = 0.4 train_set = {2:[], 4:[]} test_set = {2:[], 4:[]} train_data = full_data[:-int(test_size*len(full_data))] test_data = full_data[-int(test_size*len(full_data)):] for i in train_data: train_set[i[-1]].append(i[:-1]) for i in test_data: test_set[i[-1]].append(i[:-1]) correct = 0 total = 0 for group in test_set: for data in test_set[group]: vote,confidence = k_nearest_neighbors(train_set, data, k=5) if group == vote: correct += 1 total += 1 print('Accuracy:', correct/total) ``` ## 二十、支持向量機簡介 歡迎閱讀第二十篇。我們現在打算深入另一個監督式機器學習和分類的形式：支持向量機。 支持向量機，由 Vladimir Vapnik 在上個世紀 60 年代發明，但是 90 年代之前都被忽視，并且是最熱門的機器學習分類器之一。 支持向量的目標就是尋找數據之間的最佳分割邊界。在二維空間中，你可以將其看做分隔你的數據集的最佳擬合直線。使用支持向量機，我們在向量空間中處理問題，因此分隔直線實際上是個單獨的超平面。最佳的分隔超平面定義為，支持向量之間間距“最寬”的超平面。超平面也可以叫做決策邊界。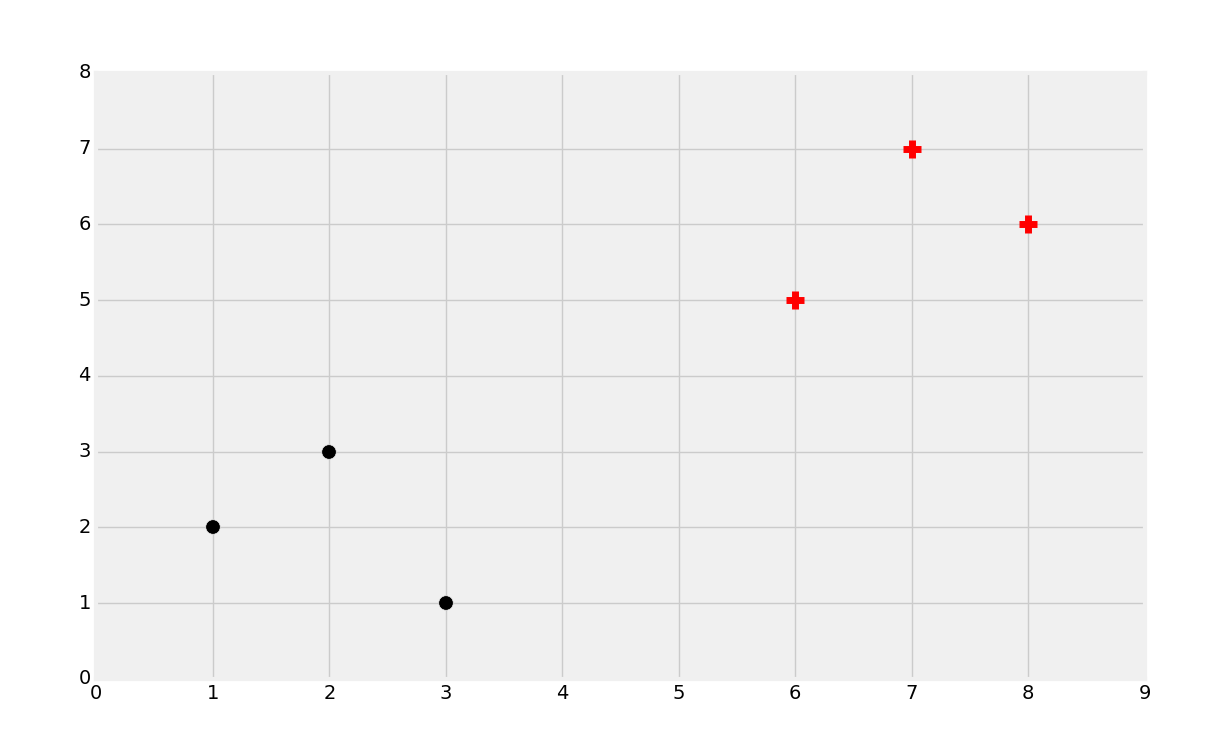最簡單的講解方式就是圖片：  我們會使用上面的數據開始。我們注意到，之前最普遍的直覺就是，你會將一個新的點基于它的近鄰來分類，這就是 KNN 的工作原理。這個方式的主要問題是，對于每個數據點，你將其與每個其它數據點比較，來獲取距離，因為算法不能很好擴展，盡管準確率上很可靠。支持向量機的目標就是，一次性生成“最佳擬合”直線（實際上是個平面，甚至是個超平面），他可以最優劃分數據。一旦計算出了超平面，我們就將其作為決策邊界。我們這樣做，因為決策邊界劃分兩個分類的數據。一旦我們計算了決策邊界，我們就再也不需要計算了，除非我們重新訓練數據集。因此，算法易于擴展，不像 KNN 分類器。 好奇之處在于，我們如何找出最佳分隔超平面？我們可以先使用眼睛來找。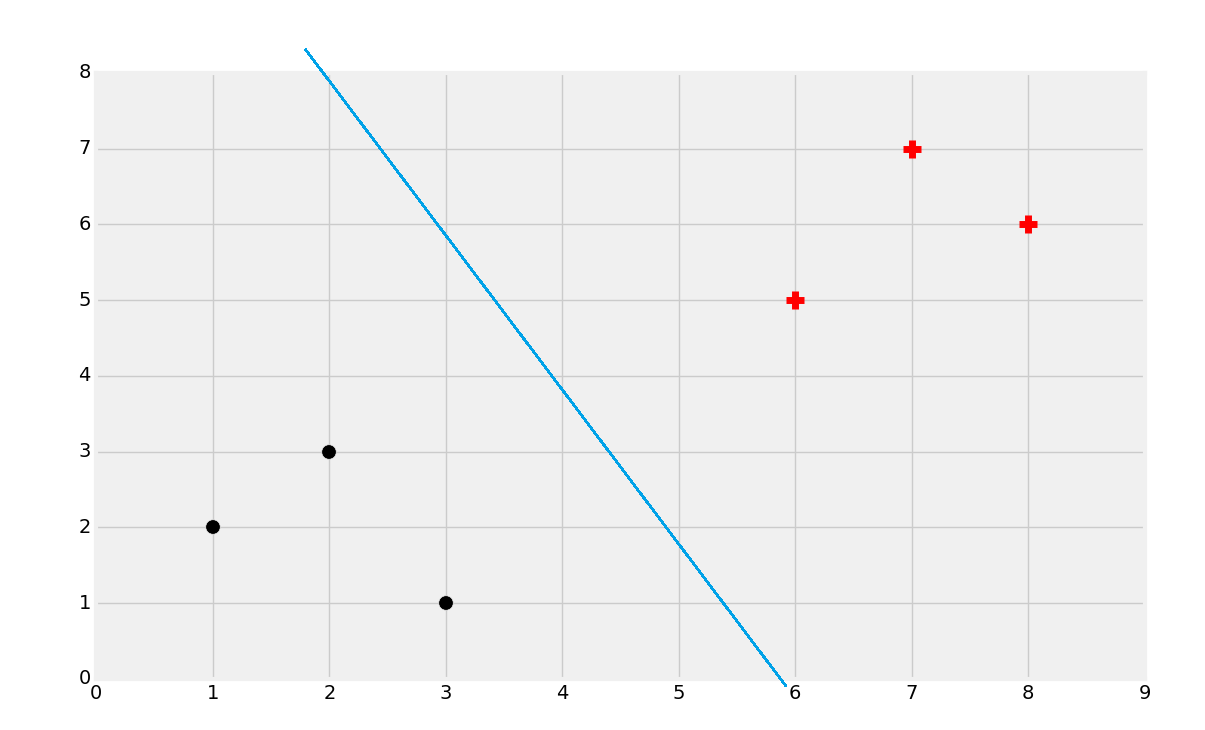  這幾乎是爭取的，但是如何尋找呢？首先尋找支持向量。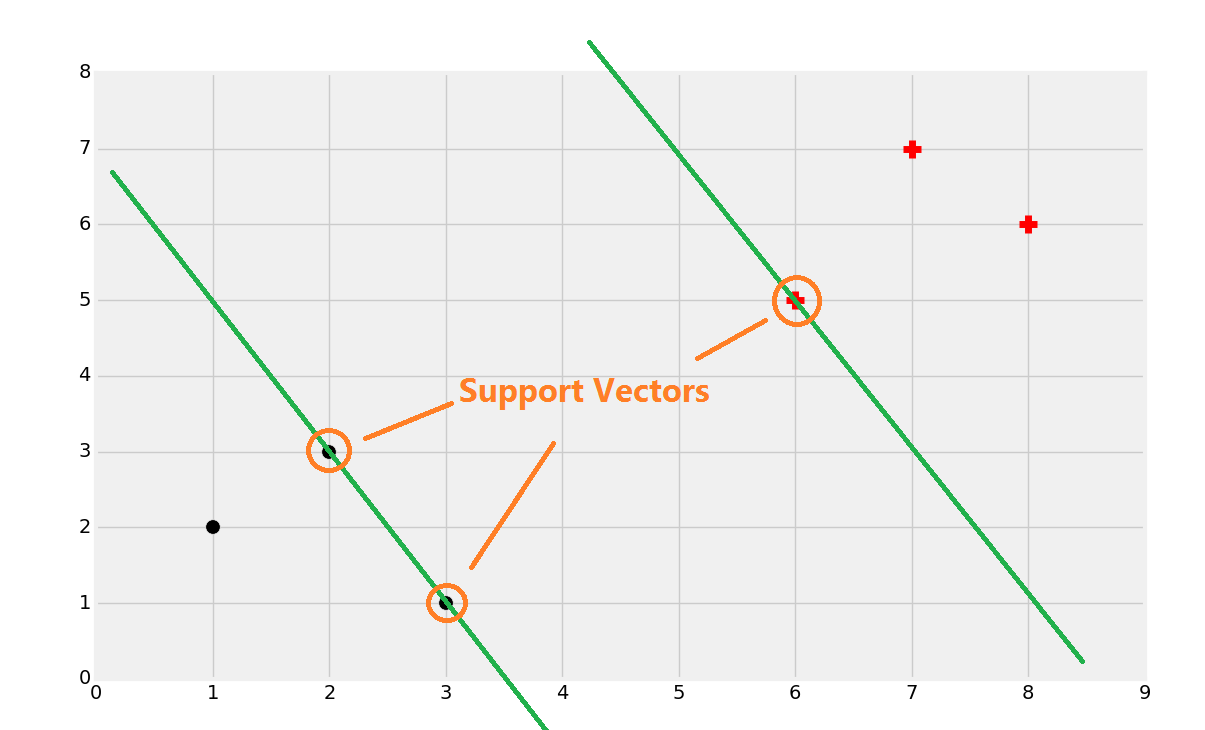  一旦你找到了支持向量，你就可以創建直線，最大分隔彼此。這里，我們可以通過計算總寬度來輕易找到決策邊界。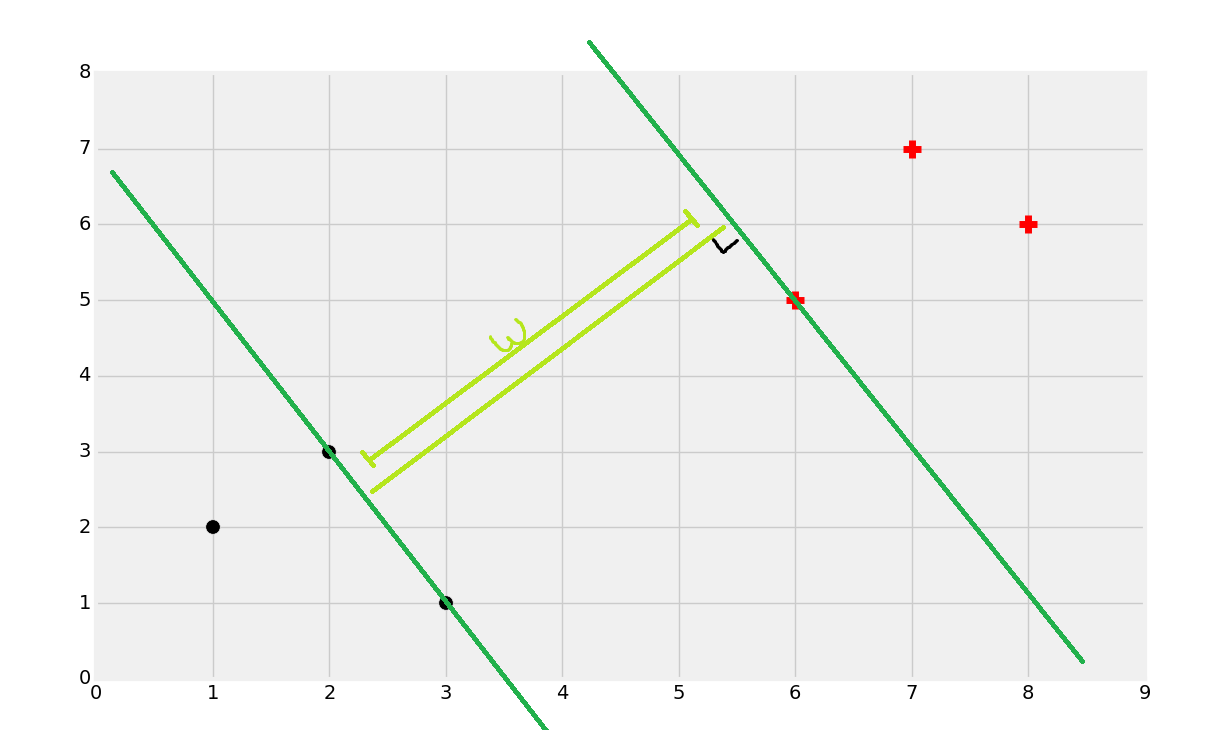  一分為二。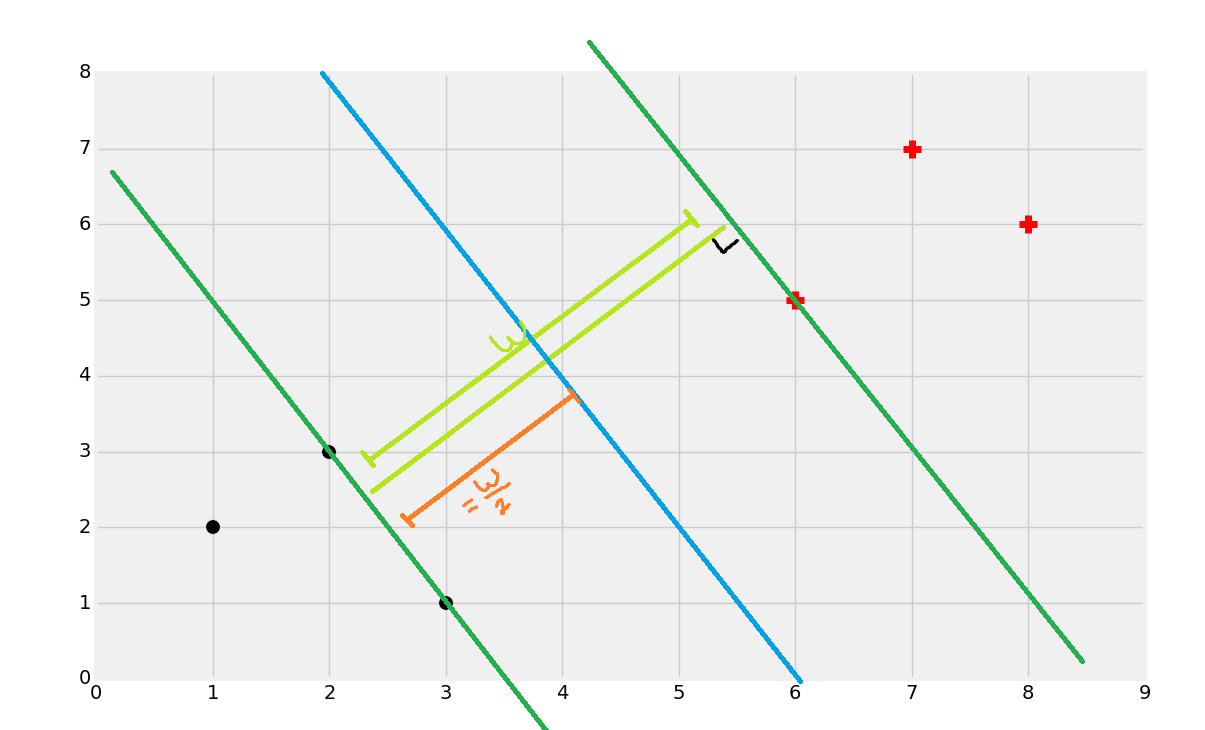  你就會得到邊界。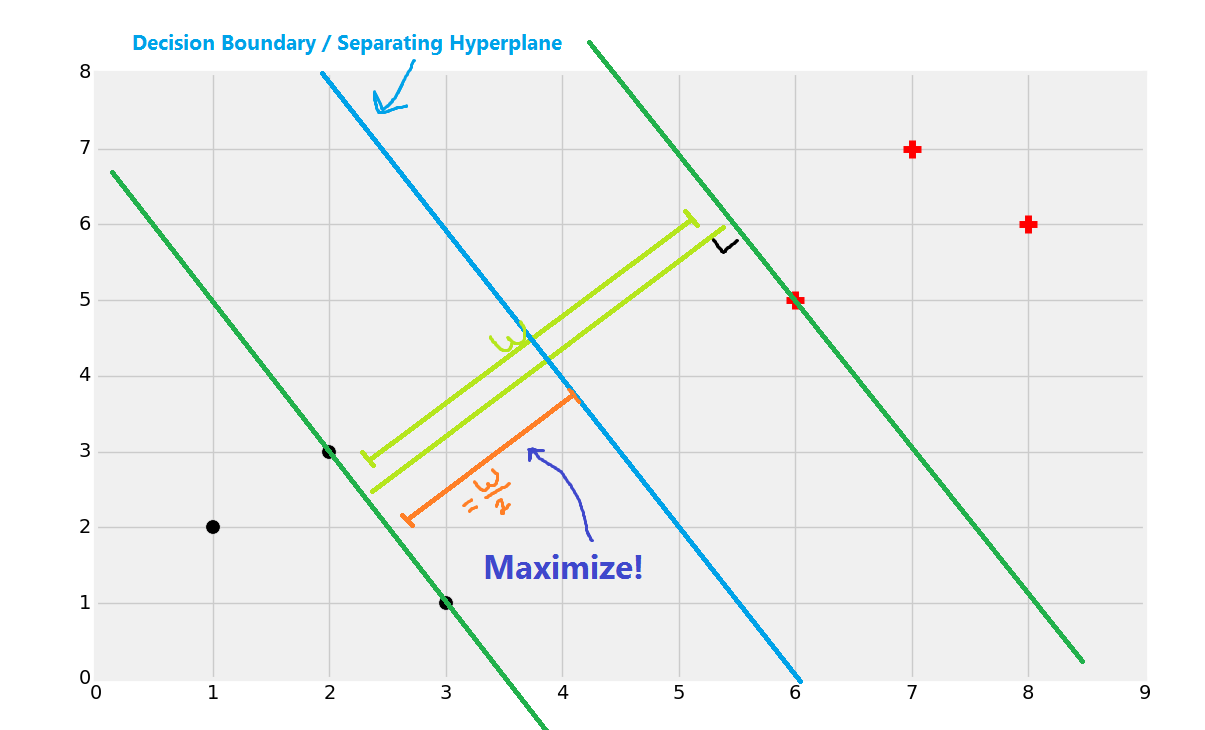  現在如果一個點位于決策邊界或者分割超平面的左側，我們就認為它是黑色分類，否則就是紅色分類。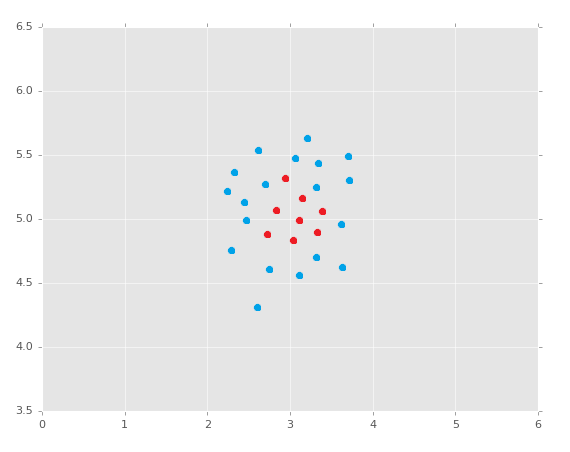 值得注意的是，這個方式本質上只能處理線性分隔的數據，如果你的數據是：  這里你能夠創建分隔超平面嘛？不能。還有沒有辦法了？當我們深入支持向量機的時候，我會讓你考慮這個問題。這里是使用 Sklearn 非常方便的原因。記得我們之前使用 Sklearn KNN 分類器的代碼嘛？這里就是了。 ```py import numpy as np from sklearn import preprocessing, cross_validation, neighbors import pandas as pd df = pd.read_csv('breast-cancer-wisconsin.data.txt') df.replace('?',-99999, inplace=True) df.drop(['id'], 1, inplace=True) X = np.array(df.drop(['class'], 1)) y = np.array(df['class']) X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size=0.2) clf = neighbors.KNeighborsClassifier() clf.fit(X_train, y_train) confidence = clf.score(X_test, y_test) print(confidence) example_measures = np.array([[4,2,1,1,1,2,3,2,1]]) example_measures = example_measures.reshape(len(example_measures), -1) prediction = clf.predict(example_measures) print(prediction) ``` 我們只需要改動兩個地方，第一個就是從`sklearn`導入`svm`。第二個就是使用支持向量分類為，它是`svm.SVC`。改動之后是： ```py import numpy as np from sklearn import preprocessing, cross_validation, neighbors, svm import pandas as pd df = pd.read_csv('breast-cancer-wisconsin.data.txt') df.replace('?',-99999, inplace=True) df.drop(['id'], 1, inplace=True) X = np.array(df.drop(['class'], 1)) y = np.array(df['class']) X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size=0.2) clf = svm.SVC() clf.fit(X_train, y_train) confidence = clf.score(X_test, y_test) print(confidence) example_measures = np.array([[4,2,1,1,1,2,3,2,1]]) example_measures = example_measures.reshape(len(example_measures), -1) prediction = clf.predict(example_measures) print(prediction) # 0.978571428571 # [2] ``` 取決于你爹隨機樣例，你應該得到 94% 到 99% ，平均值為 97%。同樣，對操作計時，要記得我通過 Sklearn 執行 KNN 代碼花費了 0.044 秒。使用`svm.SVC`，執行時間僅僅是 0.00951，在這個非常小的數據集上也有 4.6 倍。 所以我們可以認為，支持向量機似乎有同樣的準確度，但是速度更快。要注意如果我們注釋掉丟棄 ID 列的代碼，準確率會降到 60%。支持向量機通常比 KNN 算法處理大量數據要好，并且處理離群點要好。但是，這個例子中，無意義數據仍然會誤導它。我們之前使用默認參數，查看[支持向量機的文檔](https://scikit-learn.org/stable/modules/generated/sklearn.svm.SVC.html)，確實有一些參數，我們不知道它們干什么用。在后面的教程中，我們打算深入支持向量機算法，以便我們能夠實際理解所有這些參數的含義，以及它們有什么影響。雖然我們在這里告一段落，思考一下：如何處理非線性分隔，多個分類的數據和數據集（由于 SVM 是個二元分類器，也就是它生成直線來劃分兩個分組）。 ## 二十一、向量基礎 歡迎閱讀第二十一篇教程，下面就是支持向量機的部分了。這個教程中，我們打算設計一些向量的基礎，它們是支持向量機概念的組成部分。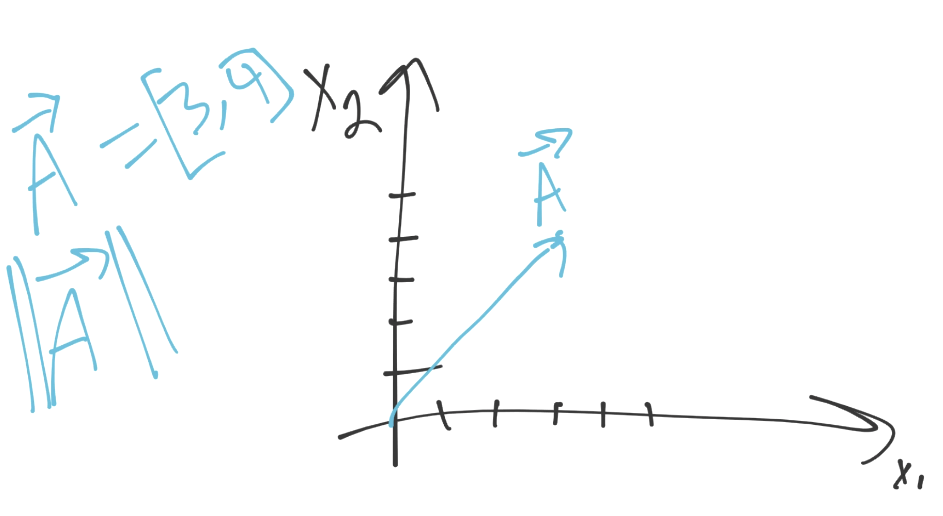 首先，向量擁有模（大小）和方向：  上面的例子中，向量 A（使用字母上面的箭頭來表示），向`[3, 4]`移動。可以將每個坐標看做該維度上的方向。我們這里，有兩個維度。我們在第一維里面移動 3 個單位，第二維里面移動 4 個。這就是方向了，那么模是什么呢？我們之前看到過它，它就是歐氏距離，范式，或者是大小。對我們來說，最重要的是，它們的計算方式相同（平方和的平方根）。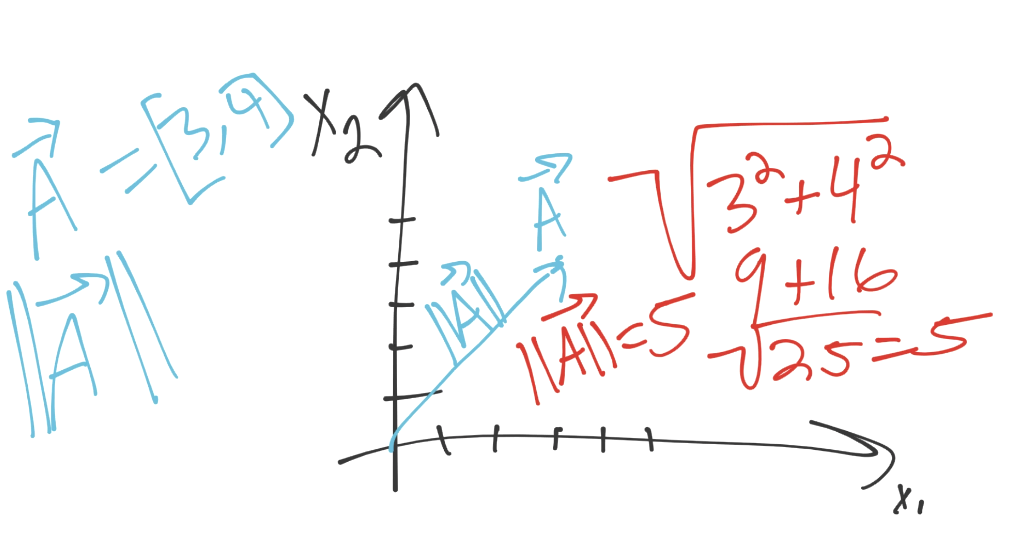  我們這里，向量的模是 5。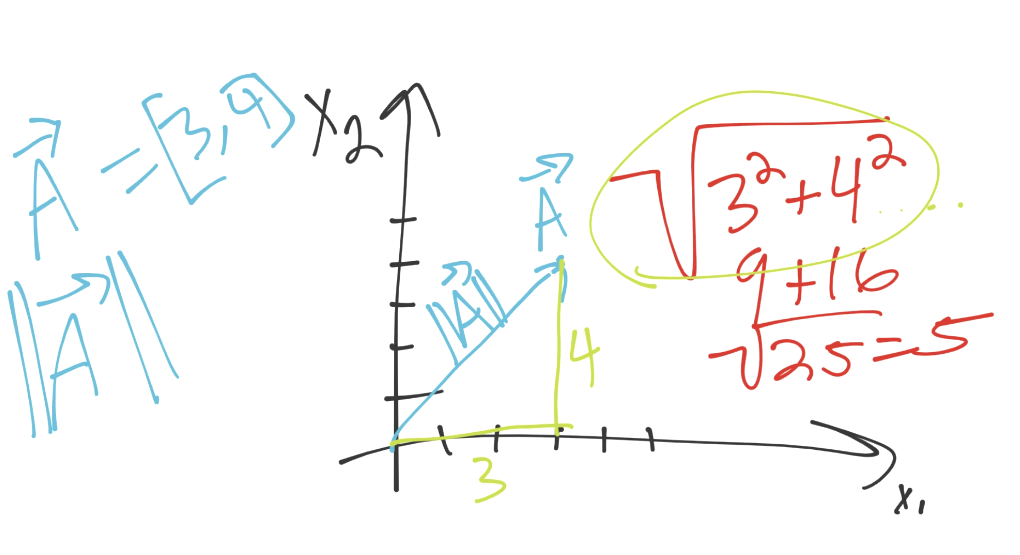如果你仔細觀察圖片，你可能會注意一些其它東西：  看起來像是直角三角形的勾股（帕斯卡）定理。的確是相同的公式，只要我們進入更高的維度，它就不是簡單的三角形了。 很簡單，下面是點積。如果我們對向量計算點積會發生什么呢？假設有兩個向量，A 和 B。A 是`[1, 3]`，B 是`[4, 2]`。我們所做的是，將對應分量相乘再相加。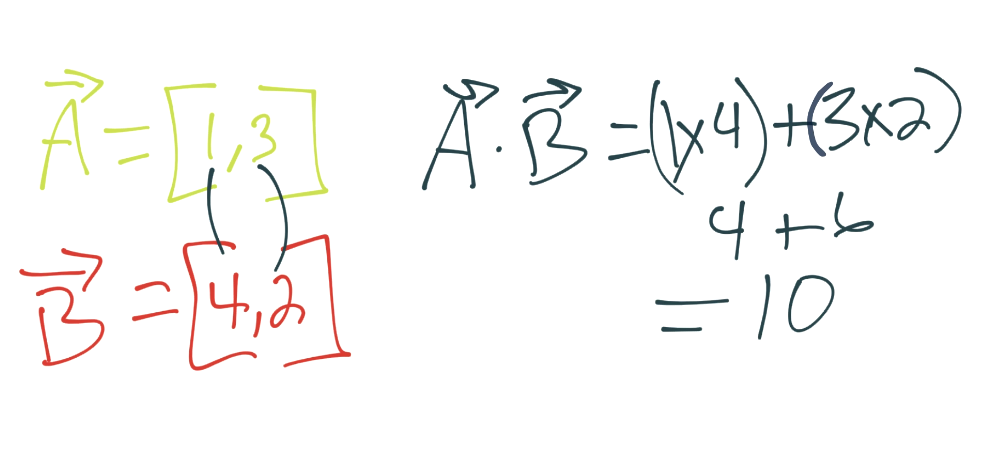例如：  好的，既然我們知道了這些東西，我們就要講解支持向量機本身了。我們作為科學家，首先會在機器上做一些斷言。 ## 二十二、支持向量斷言 歡迎閱讀機器學習教程的第二十二章。這個教程中，我們會涉及一些 SVM 的斷言。理解這些斷言，它們中一些是約束，是是理解 SVM 的數學與美的一部分。 首先，讓我們看一看 SVM 的示例目標。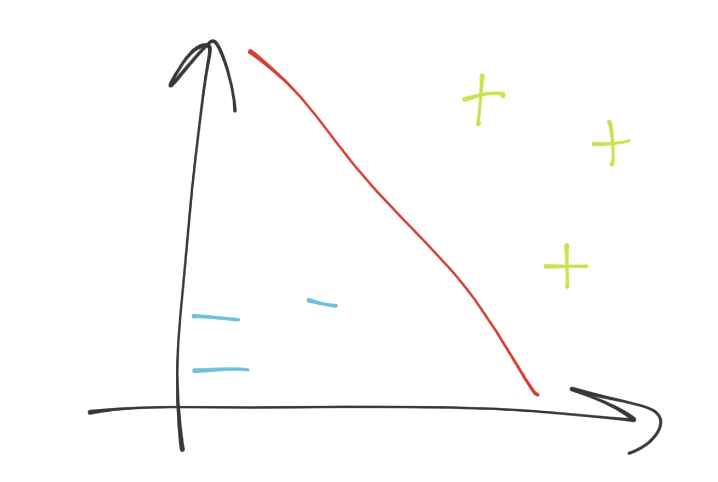它的理念是接受已知數據，之后 SVM 的擬合或者訓練是個最優化問題，尋找數據的最佳分隔直線，也就是決策邊界，像這樣：  我們在二維空間中，所以分隔超平面（決策邊界）也就是簡單的直線（紅色直線）。決策邊界分隔了藍色減號分組，和綠色加號分組。下面，如果我們在圖中任意位置放一個點，我們就可以做一個簡單的檢查，來看看它位于分隔直線的哪一邊，我們就會有答案了。是不是很簡單？如果我們僅僅停留在二維空間，我們這里的維度是什么呢？每個特征都是一個維度，所有特征組成了我們的特征集。因此，我們可能擁有一條簡單的直線，超級簡單。我們可以使用線性代數來解決它。但如果我們擁有 63 個特征，也就是 63 維呢？ 目前為止還不清楚，但是勾股定理多于二維是沒問題的。好的，我們來看看向量空間吧。我們現在在向量空間中了，我們擁有了未知的特征集，記為`v`。之后，我們有了另一個向量（法向量），和決策邊界正交，記為`w`。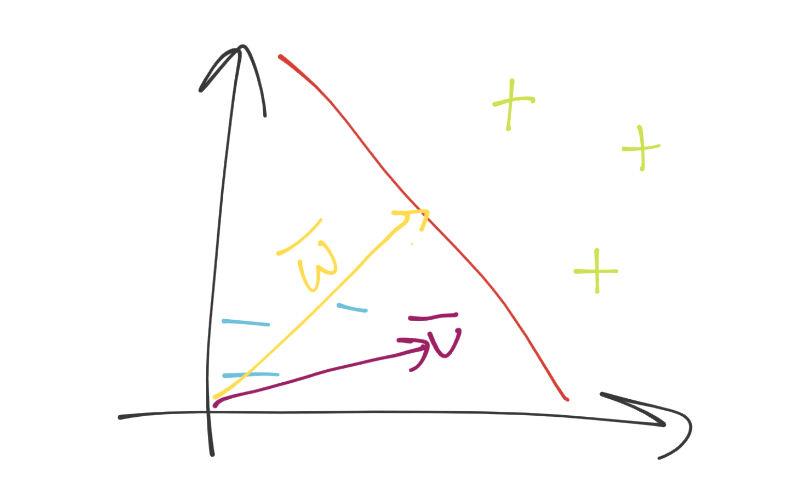看起來是：  現在如何呢？我們可以用眼睛看出來，但是如何用數學表達呢？同樣，要記得你需要一個方法，在 2 維和 5902 維都工作。你可以僅僅將向量`v`和`w`點乘，并加上一些偏移`b`（就是超平面的一般式方程），之后觀察這個值大于還是小于 0。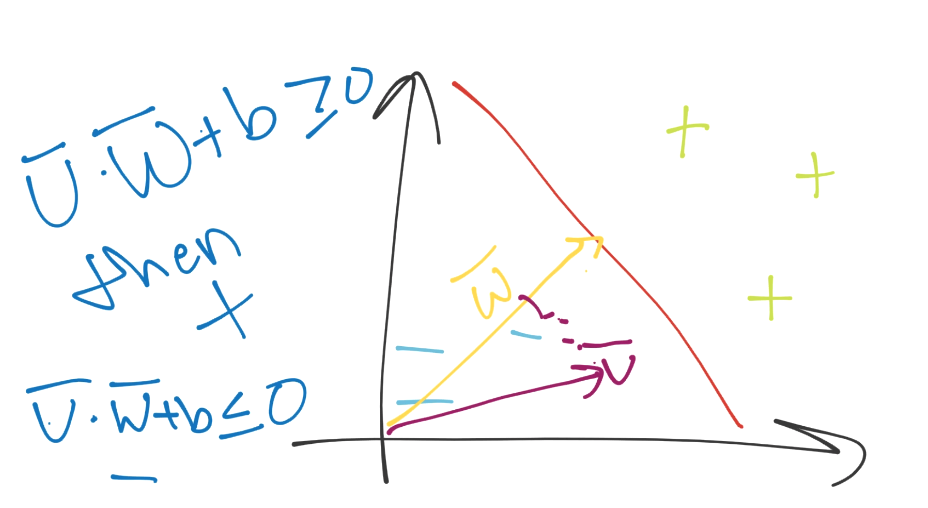  好的，盡管我們這里不知道`w`和`b`都是什么。 然后就復雜了。 我們有了兩個未知變量，并且有個壞消息：我們要求解它們。根據優化來說，這應該是個危險信號，也就是有無限個`w`和`b`滿足我們的方程，但是我們也知道有一種約束，已經在我們的腦子里定義了邏輯：我們想要最佳的分隔超平面。我們可以大致猜測這是`w`和`b`優化的一部分。最開始我們打算設置一些真實的數學約束。 目前為止，我們僅僅看到了分隔超平面，但是分隔超平面在兩個超平面之間。所謂的支持向量經過兩個超平面，這些支持向量是特征集（圖上的數據點），如果移動了它們，就會對最佳分隔超平面有影響。 由于這些支持向量會產生重大影響，我們打算為其設置一個常量值。前面說，分類函數是`sign(x·w + b)`，如果它是 0，那就說明在決策邊界上。如果大于零，就是正向分類，如果小于零，就是負向分類。我們打算利用它，并且認為，如果`x·w + b`為 1，就是正向支持向量，如果為 -1，就是負向支持向量。如果一個未知值是 -0.52，仍然是負向分類，即使它沒有超過支持向量的標記 -1。我們簡單使用支持向量來幫助我們選取最佳分隔超平面，這就是它們的作用。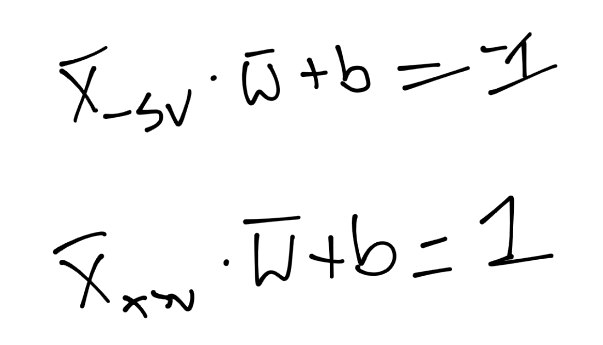我們的斷言是：  也就是說，第一行，我們讓`X`負向支持向量（這是任何為負向支持向量的特征）點乘向量`w`再加`b`等于 -1。我們斷言了這個。之后對正向支持向量：`X`正向支持向量點乘向量`w`再加`b`為正一。同樣，我們剛開始，沒有真正的證明，我們剛剛說這是一個案例。現在，我們打算引入新的值，`Yi`。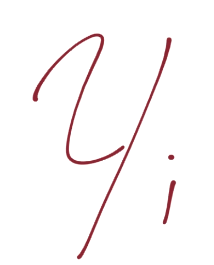  y 在 Python 代碼中是我們的分類，這里也是。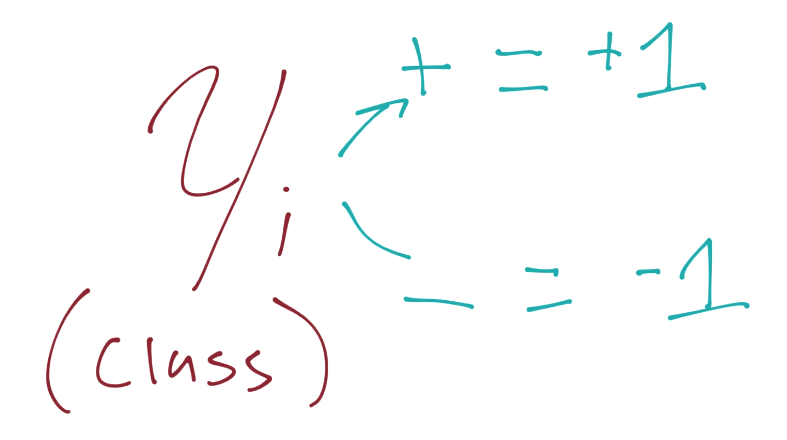  我們打算向之前的斷言引入它，如果你記得正向和負向支持向量的值：`x·w+b=1`是正向，`x·w+b=-1`是負向。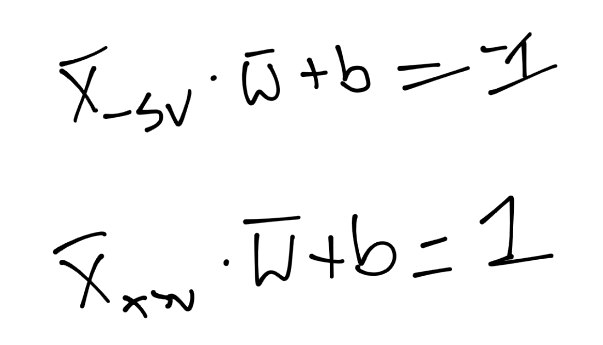我們打算將我們的原始斷言相乘：  根據這個新的`Yi`值，它同樣是 -1 或者 1（取決于分類是 -1 還是 1）。當我們將原始斷言相乘時，我們就需要將兩邊都乘`Yi`，也就是：  我們將`Yi`的符號留在左邊，但是我們實際上將其應用到了右邊（1 或者 -1）。這樣意味著對于正向支持向量，我們得到了`1x1=1`，對于負向支持向量，我們得到了`(-1)x(-1)=1`，也等于 1。我們可以將每個方程的右邊設為 0，通過兩邊都減一，我們就有了相同的方程`Yi(Xi·w+b)-1 = 0`。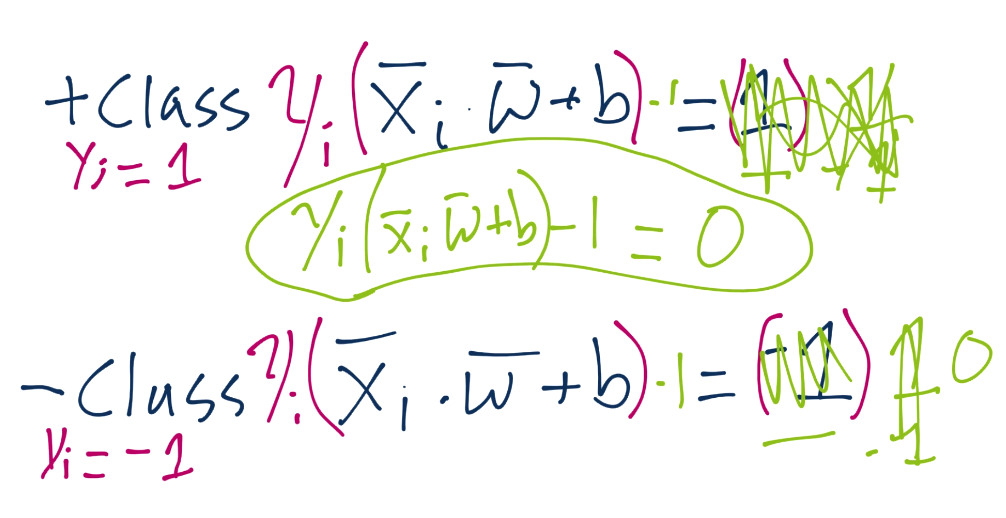  現在我們擁有了約束，下個教程中我們會深入講解。 ## 二十三、支持向量機基礎 歡迎閱讀第二十三篇教程。這篇教程中，我們打算為支持向量機的優化來解方程。 我們需要計算的支持向量為：`Yi(Xi·w+b)-1 = 0`。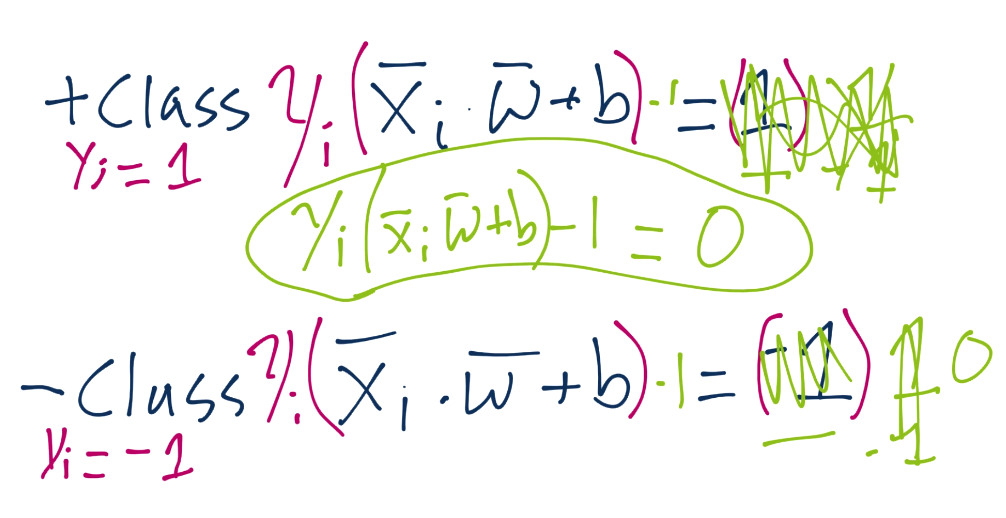  現在我們打算討論一下，我們如何處理這個支持向量機的形式優化問題。特別是，我們如何獲取向量`w`和`b`的最優解。我們也會涉及一些支持向量機的其它基礎。 開始，之前說過超平面的定義為`w·x+b`。因此，我們斷言了該方程中支持向量機的定義，正向類為 1，負向類為 -1。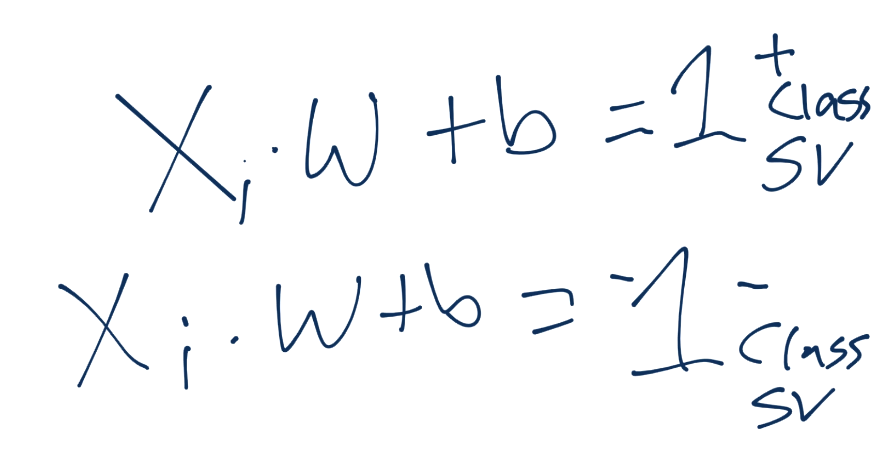  我們也推測，一旦我們找到了滿足約束問題（`w`的模最小，`b`最大）的`w`和`b`，我們用于未知點的分類決策函數，只需要簡單計算`x·w+b`。如果值為 0.99 呢？它在圖中是什么樣子？  所以它并不在正向支持向量平面上，但是很接近了。它超過了決策邊界沒有？是的，決策邊界是`x·w+b=0`。因此，未知數據集的實際決策函數只是`sign(x·w+b)`。就是它了。如果它是正的，就是`+`分類，負的就是`-`分類。現在為了求得這個函數，我們需要`w`和`b`。我們的約束函數，`Yi(Xi·W+b) >= 1`，需要滿足每個數據集。我們如何使其大于等于 1 呢？如果不乘 Yi，就僅僅需要我們的已知數據集，如果代入`x·w+b`大于 1 或者小于 -1，盡管我們之前提到過，0.98 的值也是正向分類。原因就是，新的或者未知的數據可以位于支持向量平面和決策邊界之間，但是訓練集或已知數據不可以。 于是，我們的目標就是最小化`|w|`，最大化`b`，并保持`Yi(X·W+b)>=1`的約束。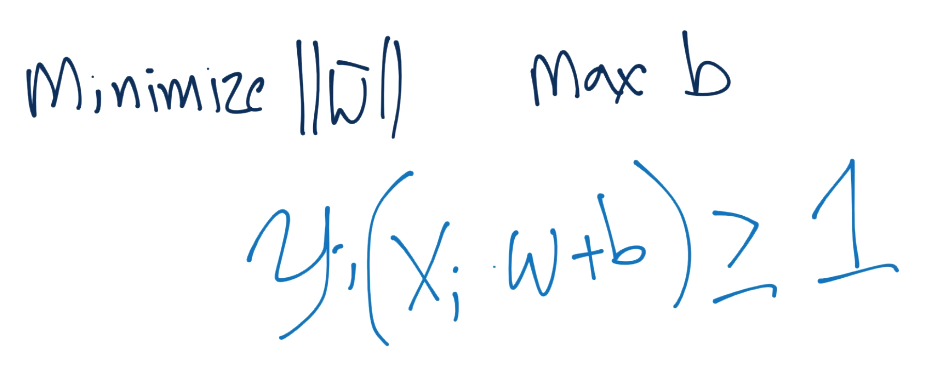  要注意，我們嘗試滿足向量`w`的約束，但是我們需要最小化`w`的模，而不是`w`，不要混淆。 有許多方式來計算這個帶約束的最優化。第一個方式就是支持向量機的傳統描述。開始，我們嘗試將分隔超平面之間的寬度最大化。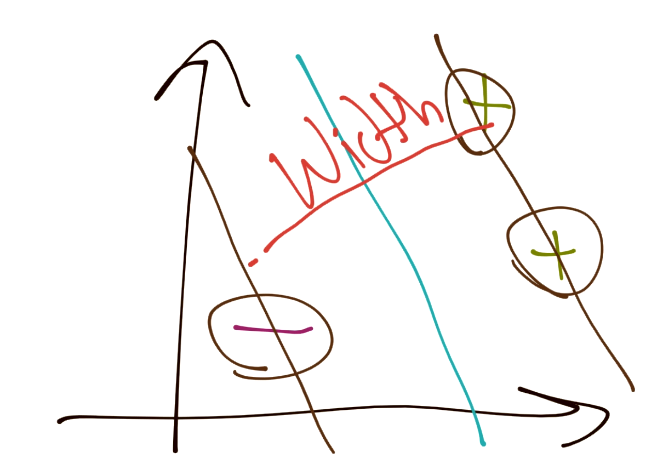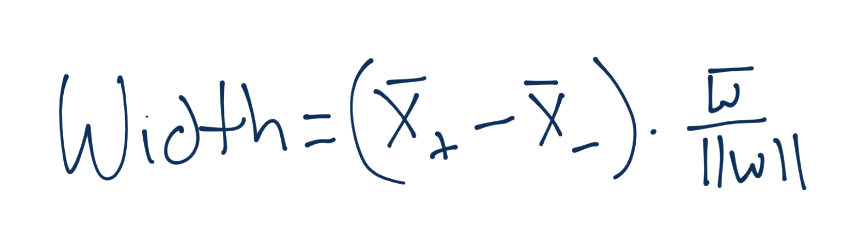  下面，向量之間的距離可以記為：  要注意，這里我們得到了`X+`和`X-`，這是兩個超平面，我們嘗試最大化之間的距離。幸運的是，這里沒有`b`，非常好。那么，`X+`和`X-`又是什么呢？我們知道嗎？是的，我們知道。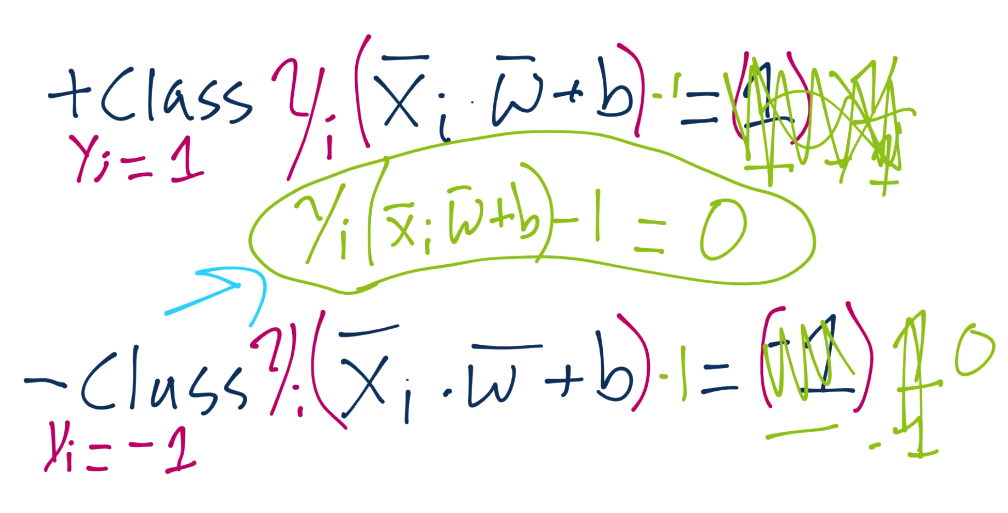  這里就有`b`了。總有一天我們會將其解出來。無論如何，我們做一些代數，將`X+`和`X-`替換為`1-b`和`1+b`。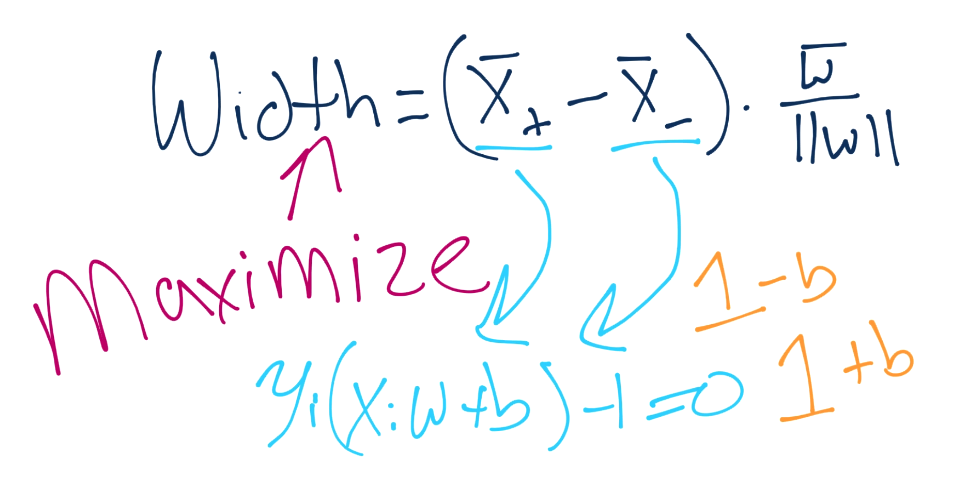  記得你的操作順序嗎？這非常方便，我們就將`b`移走了，現在我們的方程極大簡化了。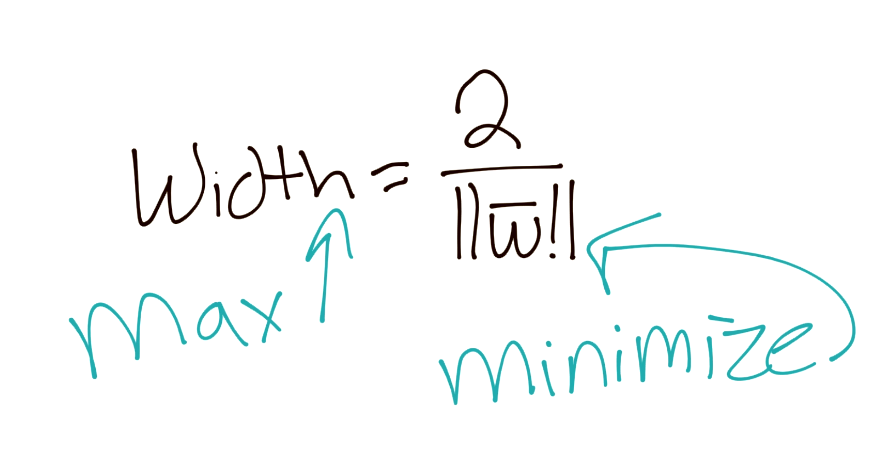  為了更好地滿足我們未來的要求，我們可以認為，如果我們打算最大化`2/|w|`，我們就可以最小化`|w|`，這個之前已經講過了。由于我們打算最小化`|w|`，相當于最小化`1/2 * |w|^2`：  我們的約束是` Yi(Xi·W+b)-1 = 0`。因此，所有特征集的和應該也是 0。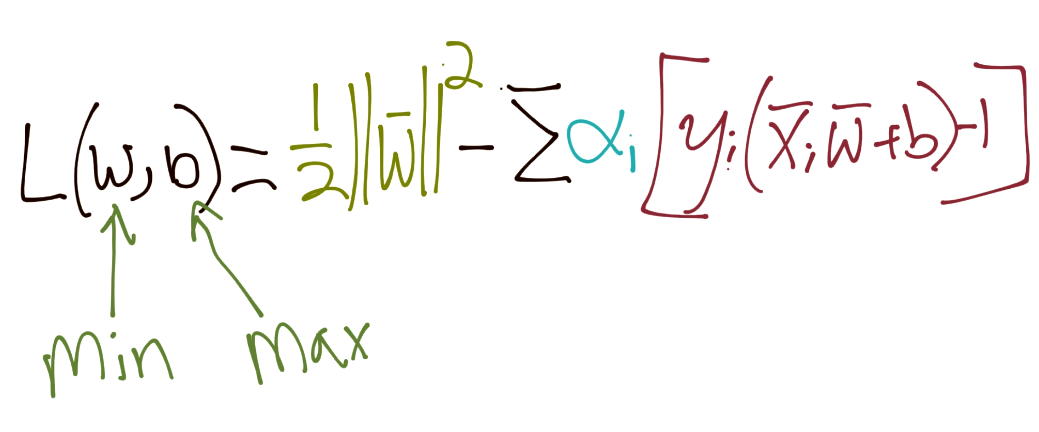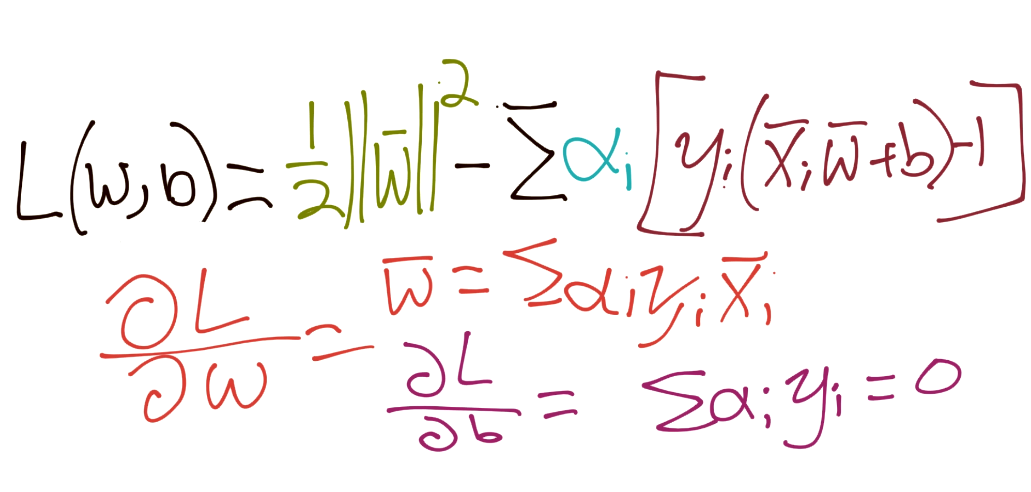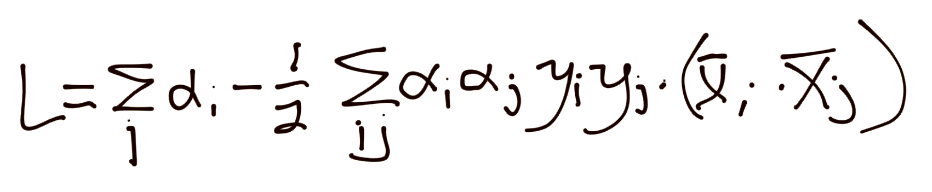所以我們引入了拉格朗日乘數法：  在這里求導：  把所有東西放到一起：  于是，如果你沒有對求出來的東西不滿意，你就到這里了。我們得到了`alpha`的平方，也就是說，我們需要解決一個平方規劃。 很快就變復雜了。 下一篇教程中，我們的興趣是從零編寫 SVM，我們看看是否可以將其簡化。 ## 二十四、約束優化 歡迎閱讀第二十四篇教程。這個教程中，我們打算深入討論 SVM 的約束優化。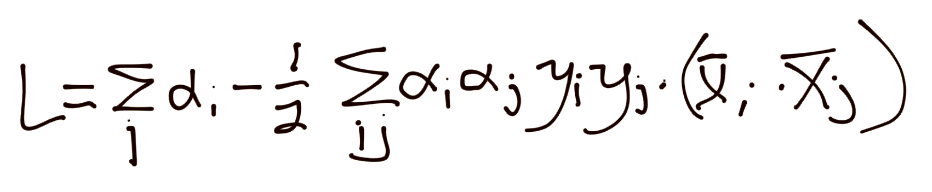 上一個教程中，我們剩下了 SVM 的形式約束優化問題：  看起來很丑陋，并且由于`alpha`的平方，我們看到了一個平方規劃問題，這不是很容易完成。約束優化不是一個很大的范圍嗎？有沒有別的方式？你怎么問我會很高興，因為是的，的確存在其他方式。SVM 的優化問題是個凸優化問題，其中凸優化的形狀是`w`的模。  這個凸優化的目標是尋找`w`的最大模。一種解決凸優化問題的方式就是“下降”，直到你不能再往下走了。一旦你到達了底部，你就能通過其他路徑慢慢回去，重復這個步驟，直到你到達了真正的底部。將凸優化問題看做一個碗，求解過程就是沿著碗的邊緣扔進去一個球。球會很快滾下邊緣，正好達到最中間的位置，之后可能會在另一側上升，但是會再次下降，沿著另一個路徑，可能會重復幾次，每次都會移動得更慢，并且距離更短，最終，球會落在碗的底部。 我們會使用 Python 來模擬這個十分相同的問題。我們會專注于向量`w`，以一個很大的模來開始。之前提到過向量的模就是分量的平方和的平方根。也就是說，向量`w`為`[5,5]`或者`[-5,5]`的模都一樣。但是和特征集的點積有很大不同，并且是完全不同的超平面。出于這個原因，我們需要檢查每個向量的每個變種。 我們的基本思想就是像一個球那樣，快速沿側壁下降，重復知道我們不能再下降了。這個時候，我們需要重復我們的最后幾個步驟。我們以更小的步驟來執行。之后可能將這個步驟重復幾次，例如：  首先，我們最開始就像綠色的線，我們用大的步長下降。我們會繞過中心，之后用更小的步長，就像紅色的線。之后我們會像藍色的線。這個方式，我們的步長會越來越小（每一步我們都會計算新的向量`w`和`b`）。這樣，我們就可以獲取最優化的向量`w`，而不需要一開始就使用較大的步長來完成相同結果，并且在處理時浪費很多時間。 如果我們找到了碗或者凸形狀的底部，我們就說我們找到了全局最小值。凸優化問題非常好的原因，就是我們可以使用這個迭代方式來找到底部。如果不是凸優化，我們的形狀就是這樣：  現在，當從左側開始時，你可能檢測到上升了，所以你返回并找到了局部最小值。  再說一遍，我們在處理一個很好的凸優化問題，所以我們不需要擔心錯誤。我的計劃就是給定一個向量，緩慢減小向量的模（也就是講笑向量中數據的絕對值）。對于每個向量，假設是`[10, 10]`，我們會使用這些東西來變換向量：`[1,1],[-1,1],[-1,-1],[1,-1]`。這會向我們提供這個向量的所有變種，我們需要檢查它們，盡管它們擁有相同的模。這就是下個教程中要做的事情。 ## 二十五、使用 Python 從零開始編寫 SVM 歡迎閱讀第 25 篇教程，下面就是我們的 SVM 部分了。這個教程中，我們打算從零編寫 SVM。 在深入之前，我們會專注于一些選項，用于解決約束優化問題。 首先，約束優化的話題很多，也有很多材料。即使是我們的子話題：凸優化，也是很龐大的。一個不錯的起始點是 <https://web.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf>。對于約束優化，你可以查看 <http://www.mit.edu/~dimitrib/Constrained-Opt.pdf>。 特別是在 Python 中，[CVXOPT](http://cvxopt.org/) 包擁有多種凸優化方法，其中之一就是我們的平方規劃問題（`cvxopt.solvers.qp`）。 同樣，也有[ libsvm 的 Python 接口](https://github.com/cjlin1/libsvm/tree/master/python)，或者[ libsvm 包](https://www.csie.ntu.edu.tw/~cjlin/libsvm/)。我們選擇不要用這些東西，因為 SVM 的最優化問題幾乎就是 SVM 問題的全部了。 現在，為了使用 Python 來開始寫 SVM，我們以這些導入來開始。 ```py import matplotlib.pyplot as plt from matplotlib import style import numpy as np style.use('ggplot') ``` 我們使用 Matplotlib 來繪圖，NumPy 來處理數組。下面我們會擁有一些起始數據： ```py data_dict = {-1:np.array([[1,7], [2,8], [3,8],]), 1:np.array([[5,1], [6,-1], [7,3],])} ``` 現在我們打算開始構建我們的 SVM 類。如果你不熟悉面向對象編程，不要害怕。我們這里的例子是個非常基本的 OOP 形式。只要知道 OOP 創建帶有對象，類中帶有屬性、函數（實際上是方法），以及我們使用`self`變量來代表對象本身。解釋再多也沒有意義，已經足以開始了。如果你對代碼感到疑惑，可以去在線社區提問。 ```py class Support_Vector_Machine: def __init__(self, visualization=True): self.visualization = visualization self.colors = {1:'r',-1:'b'} if self.visualization: self.fig = plt.figure() self.ax = self.fig.add_subplot(1,1,1) ``` 類的`__init__`方法是使用類創建對象時，執行的方法。其它方法只在調用時執行。對于每個方法，我們傳入`self`作為第一個參數，主要是一種約定。下面，我們添加可視化參數。我們想看看 SVM，所以將其設為`True`。下面米可以看見一些變量，例如`self.color`和`self.visualization`。這樣做能夠讓我們在類的其它方法中，引用`self.color`，最后，如果我們開啟了可視化，我們打算繪制我們的圖像。 下面，讓我們繼續并體感家更多方法：`fit`和`predict`。 ```py class Support_Vector_Machine: def __init__(self, visualization=True): self.visualization = visualization self.colors = {1:'r',-1:'b'} if self.visualization: self.fig = plt.figure() self.ax = self.fig.add_subplot(1,1,1) # train def fit(self, data): pass def predict(self,features): # sign( x.w+b ) classification = np.sign(np.dot(np.array(features),self.w)+self.b) return classification ``` `fit`方法會用于訓練我們的 SVM。這就是最優化的步驟。一旦我們完成了訓練，`predict`方法會預測新特征集的值，一旦我們知道了`w`和`b`，它就是`sign(x·w+b)`。 目前為止的代碼。 ```py import matplotlib.pyplot as plt from matplotlib import style import numpy as np style.use('ggplot') class Support_Vector_Machine: def __init__(self, visualization=True): self.visualization = visualization self.colors = {1:'r',-1:'b'} if self.visualization: self.fig = plt.figure() self.ax = self.fig.add_subplot(1,1,1) # train def fit(self, data): pass def predict(self,features): # sign( x.w+b ) classification = np.sign(np.dot(np.array(features),self.w)+self.b) return classification data_dict = {-1:np.array([[1,7], [2,8], [3,8],]), 1:np.array([[5,1], [6,-1], [7,3],])} ``` 下個教程中，我們會繼續并開始處理`fit`方法。 ## 二十六、支持向量機優化 歡迎閱讀第二十六篇教程，下面就是我們的支持向量機章節。這篇教程中，我們打算處理 SVM 的優化方法`fit`。 目前為止的代碼為： ```py import matplotlib.pyplot as plt from matplotlib import style import numpy as np style.use('ggplot') class Support_Vector_Machine: def __init__(self, visualization=True): self.visualization = visualization self.colors = {1:'r',-1:'b'} if self.visualization: self.fig = plt.figure() self.ax = self.fig.add_subplot(1,1,1) # train def fit(self, data): pass def predict(self,features): # sign( x.w+b ) classification = np.sign(np.dot(np.array(features),self.w)+self.b) return classification data_dict = {-1:np.array([[1,7], [2,8], [3,8],]), 1:np.array([[5,1], [6,-1], [7,3],])} ``` 我們開始填充`fit`方法： ```py def fit(self, data): self.data = data # { ||w||: [w,b] } opt_dict = {} transforms = [[1,1], [-1,1], [-1,-1], [1,-1]] ``` 要注意這個方法首先傳遞`self`（記住這是方法的約定），之后傳遞`data`。`data`就是我們我們打算訓練或者優化的數據。我們這里，它是`data_dict`，我們已經創建好了。 我們將`self.data`設為該數據。現在，我們可以在類中的任何地方引用這個訓練數據了（但是，我們需要首先使用數據來調用這個訓練方法，來避免錯誤）。 下面，我們開始構建最優化字典`opt_dict`，它包含任何最優化的值。隨著我們減小我們的`w`向量，我們會使用約束函數來測試向量，如果存在的話，尋找最大的滿足方程的`b`，之后將所有數據儲存在我們的最華友字典中。字典是`{ ||w|| : [w,b] }`。當我們完成所有優化時，我們會選擇字典中鍵最小的`w`和`b`值。 最后，我們會設置我們的轉換。我們已經解釋了我們的意圖，來確保我們檢查了每個可能的向量版本。 下面，我們需要一些匹配數據的起始點。為此，我們打算首先引用我們的訓練數據，來選取一些合適的起始值。 ```py # finding values to work with for our ranges. all_data = [] for yi in self.data: for featureset in self.data[yi]: for feature in featureset: all_data.append(feature) self.max_feature_value = max(all_data) self.min_feature_value = min(all_data) # no need to keep this memory. all_data=None ``` 我們所做的就是遍歷所有數據，尋找最大值和最小值。現在我們打算定義我們的步長。 ```py step_sizes = [self.max_feature_value * 0.1, self.max_feature_value * 0.01, # starts getting very high cost after this. self.max_feature_value * 0.001] ``` 這里我們設置了一些大小的步長，我們打算這樣執行。對于我們的第一遍，我們會采取大跨步（10%）。一旦我們使用這些步長找到了最小值，我們就將步長降至 1% 來調優。我們會繼續下降，取決于你想要多么精確。我會在這個項目的末尾討論，如何在程序中判斷是否應該繼續優化。 下面，我們打算設置一些變量，來幫助我們給`b`生成步長（用于生成比`w`更大的步長，因為我們更在意`w`的精確度），并跟蹤最后一個最優值。 ```py # extremely expensive b_range_multiple = 5 b_multiple = 5 latest_optimum = self.max_feature_value*10 ``` 現在我們開始了： ```py for step in step_sizes: w = np.array([latest_optimum,latest_optimum]) # we can do this because convex optimized = False while not optimized: pass ``` 這里的思想就是沿著向量下降。開始，我們將`optimized`設為`False`，并為我們會在每個主要步驟重置它。`optimized`變量再我們檢查所有步驟和凸形狀（我們的碗）的底部之后，會設為`True`。 我們下個教程中會繼續實現這個邏輯，那里我們會實際使用約束問題來檢查值，檢查我們是否找到了可以保存的值。 目前為止的代碼： ```py import matplotlib.pyplot as plt from matplotlib import style import numpy as np style.use('ggplot') class Support_Vector_Machine: def __init__(self, visualization=True): self.visualization = visualization self.colors = {1:'r',-1:'b'} if self.visualization: self.fig = plt.figure() self.ax = self.fig.add_subplot(1,1,1) # train def fit(self, data): self.data = data # { ||w||: [w,b] } opt_dict = {} transforms = [[1,1], [-1,1], [-1,-1], [1,-1]] all_data = [] for yi in self.data: for featureset in self.data[yi]: for feature in featureset: all_data.append(feature) self.max_feature_value = max(all_data) self.min_feature_value = min(all_data) all_data = None step_sizes = [self.max_feature_value * 0.1, self.max_feature_value * 0.01, # point of expense: self.max_feature_value * 0.001,] # extremely expensive b_range_multiple = 5 # b_multiple = 5 latest_optimum = self.max_feature_value*10 for step in step_sizes: w = np.array([latest_optimum,latest_optimum]) # we can do this because convex optimized = False while not optimized: pass def predict(self,features): # sign( x.w+b ) classification = np.sign(np.dot(np.array(features),self.w)+self.b) return classification data_dict = {-1:np.array([[1,7], [2,8], [3,8],]), 1:np.array([[5,1], [6,-1], [7,3],])} ``` ## 二十七、支持向量機優化 第二部分 歡迎閱讀第二十七篇教程，下面就是支持向量機的部分。這個教程中，我們打算繼續使用 Python 代碼處理 SVM 優化問題。 在我們停止的地方，我們的代碼為： ```py import matplotlib.pyplot as plt from matplotlib import style import numpy as np style.use('ggplot') class Support_Vector_Machine: def __init__(self, visualization=True): self.visualization = visualization self.colors = {1:'r',-1:'b'} if self.visualization: self.fig = plt.figure() self.ax = self.fig.add_subplot(1,1,1) # train def fit(self, data): self.data = data # { ||w||: [w,b] } opt_dict = {} transforms = [[1,1], [-1,1], [-1,-1], [1,-1]] all_data = [] for yi in self.data: for featureset in self.data[yi]: for feature in featureset: all_data.append(feature) self.max_feature_value = max(all_data) self.min_feature_value = min(all_data) all_data = None step_sizes = [self.max_feature_value * 0.1, self.max_feature_value * 0.01, # point of expense: self.max_feature_value * 0.001,] # extremely expensive b_range_multiple = 5 # b_multiple = 5 latest_optimum = self.max_feature_value*10 for step in step_sizes: w = np.array([latest_optimum,latest_optimum]) # we can do this because convex optimized = False while not optimized: pass def predict(self,features): # sign( x.w+b ) classification = np.sign(np.dot(np.array(features),self.w)+self.b) return classification data_dict = {-1:np.array([[1,7], [2,8], [3,8],]), 1:np.array([[5,1], [6,-1], [7,3],])} ``` 選取`while not optimized `部分： ```py optimized = False while not optimized: for b in np.arange(-1*(self.max_feature_value*b_range_multiple), self.max_feature_value*b_range_multiple, step*b_multiple): ``` 這里我們開始迭代所有可能的`b`值，并且現在可以看到，之前設置的`b`值。這里要注意，我們使用一個固定的步長，直接迭代`b`。我們也可以拆分`b`的步長，就像我們對`w`所做的那樣。為了使事情更加準確，你可能打算這樣實現。也就是說，出于簡潔，我打算跳過這個部分，因為我們要完成近似的結果。而不是嘗試獲得什么獎項。 繼續： ```py optimized = False while not optimized: for b in np.arange(-1*(self.max_feature_value*b_range_multiple), self.max_feature_value*b_range_multiple, step*b_multiple): for transformation in transforms: w_t = w*transformation found_option = True # weakest link in the SVM fundamentally # SMO attempts to fix this a bit # yi(xi.w+b) >= 1 # # #### add a break here later.. for i in self.data: for xi in self.data[i]: yi=i if not yi*(np.dot(w_t,xi)+b) >= 1: found_option = False if found_option: opt_dict[np.linalg.norm(w_t)] = [w_t,b] ``` 現在我們迭代了每個變形，對我們的約束條件測試了每個東西。如果我們數據集中的任何特征集不滿足我們的約束，我們就會去掉這個變量，因為它不匹配，并繼續。我建議在這里停頓一下。如果僅僅是一個變量不工作，你可能要放棄其余部分，因為一個變量不匹配，就足以扔掉`w`和`b`了。你應該在這里停頓，并且處理循環。現在，我們會將代碼保持原樣，但是我在錄制視頻的時候，會有所修改。 現在我們完成`fit`方法，我會貼出完整代碼并解釋差異： ```py def fit(self, data): self.data = data # { ||w||: [w,b] } opt_dict = {} transforms = [[1,1], [-1,1], [-1,-1], [1,-1]] all_data = [] for yi in self.data: for featureset in self.data[yi]: for feature in featureset: all_data.append(feature) self.max_feature_value = max(all_data) self.min_feature_value = min(all_data) all_data = None # support vectors yi(xi.w+b) = 1 step_sizes = [self.max_feature_value * 0.1, self.max_feature_value * 0.01, # point of expense: self.max_feature_value * 0.001,] # extremely expensive b_range_multiple = 5 # we dont need to take as small of steps # with b as we do w b_multiple = 5 latest_optimum = self.max_feature_value*10 for step in step_sizes: w = np.array([latest_optimum,latest_optimum]) # we can do this because convex optimized = False while not optimized: for b in np.arange(-1*(self.max_feature_value*b_range_multiple), self.max_feature_value*b_range_multiple, step*b_multiple): for transformation in transforms: w_t = w*transformation found_option = True # weakest link in the SVM fundamentally # SMO attempts to fix this a bit # yi(xi.w+b) >= 1 # # #### add a break here later.. for i in self.data: for xi in self.data[i]: yi=i if not yi*(np.dot(w_t,xi)+b) >= 1: found_option = False if found_option: opt_dict[np.linalg.norm(w_t)] = [w_t,b] if w[0] < 0: optimized = True print('Optimized a step.') else: w = w - step norms = sorted([n for n in opt_dict]) #||w|| : [w,b] opt_choice = opt_dict[norms[0]] self.w = opt_choice[0] self.b = opt_choice[1] latest_optimum = opt_choice[0][0]+step*2 ``` 一旦我們越過了`w`向量的零點，就沒有理由繼續了，因為我們通過變換測試了負值。所以我們已經完成了這個步長，要么繼續下一個步長，要么就完全完成了。如果沒有經過 0，那就向下走一步。一旦我們走完了能走的所有步驟，我們就對`opt_dict `字典的鍵數組記性排序（它包含`||w|| : [w,b]`）。我們想要向量`w`的最小模，所以我們選取列表的第一個元素。我們給這里的`self.w`和`self.b`賦值，并設置最后的優化值。之后，我們選取另一個步長，或者完全完成了整個過程（如果沒有更多的步長可選取了）。 這里，完整代碼是： ```py import matplotlib.pyplot as plt from matplotlib import style import numpy as np style.use('ggplot') class Support_Vector_Machine: def __init__(self, visualization=True): self.visualization = visualization self.colors = {1:'r',-1:'b'} if self.visualization: self.fig = plt.figure() self.ax = self.fig.add_subplot(1,1,1) # train def fit(self, data): self.data = data # { ||w||: [w,b] } opt_dict = {} transforms = [[1,1], [-1,1], [-1,-1], [1,-1]] all_data = [] for yi in self.data: for featureset in self.data[yi]: for feature in featureset: all_data.append(feature) self.max_feature_value = max(all_data) self.min_feature_value = min(all_data) all_data = None # support vectors yi(xi.w+b) = 1 step_sizes = [self.max_feature_value * 0.1, self.max_feature_value * 0.01, # point of expense: self.max_feature_value * 0.001,] # extremely expensive b_range_multiple = 5 # we dont need to take as small of steps # with b as we do w b_multiple = 5 latest_optimum = self.max_feature_value*10 for step in step_sizes: w = np.array([latest_optimum,latest_optimum]) # we can do this because convex optimized = False while not optimized: for b in np.arange(-1*(self.max_feature_value*b_range_multiple), self.max_feature_value*b_range_multiple, step*b_multiple): for transformation in transforms: w_t = w*transformation found_option = True # weakest link in the SVM fundamentally # SMO attempts to fix this a bit # yi(xi.w+b) >= 1 # # #### add a break here later.. for i in self.data: for xi in self.data[i]: yi=i if not yi*(np.dot(w_t,xi)+b) >= 1: found_option = False if found_option: opt_dict[np.linalg.norm(w_t)] = [w_t,b] if w[0] < 0: optimized = True print('Optimized a step.') else: w = w - step norms = sorted([n for n in opt_dict]) #||w|| : [w,b] opt_choice = opt_dict[norms[0]] self.w = opt_choice[0] self.b = opt_choice[1] latest_optimum = opt_choice[0][0]+step*2 def predict(self,features): # sign( x.w+b ) classification = np.sign(np.dot(np.array(features),self.w)+self.b) return classification data_dict = {-1:np.array([[1,7], [2,8], [3,8],]), 1:np.array([[5,1], [6,-1], [7,3],])} ``` 現在我們已經準備好可視化以及測試支持向量機的預測了。我們會在下一個教程中完成它們。 ## 二十八、使用我們的 SVM 來可視化和預測 歡迎閱讀第二十八篇教程。這個教程中，我們完成我們從零開始的基本 SVM，并使用它來可視化并作出預測。 我們目前為止的代碼： ```py import matplotlib.pyplot as plt from matplotlib import style import numpy as np style.use('ggplot') class Support_Vector_Machine: def __init__(self, visualization=True): self.visualization = visualization self.colors = {1:'r',-1:'b'} if self.visualization: self.fig = plt.figure() self.ax = self.fig.add_subplot(1,1,1) # train def fit(self, data): self.data = data # { ||w||: [w,b] } opt_dict = {} transforms = [[1,1], [-1,1], [-1,-1], [1,-1]] all_data = [] for yi in self.data: for featureset in self.data[yi]: for feature in featureset: all_data.append(feature) self.max_feature_value = max(all_data) self.min_feature_value = min(all_data) all_data = None # support vectors yi(xi.w+b) = 1 step_sizes = [self.max_feature_value * 0.1, self.max_feature_value * 0.01, # point of expense: self.max_feature_value * 0.001,] # extremely expensive b_range_multiple = 5 # we dont need to take as small of steps # with b as we do w b_multiple = 5 latest_optimum = self.max_feature_value*10 for step in step_sizes: w = np.array([latest_optimum,latest_optimum]) # we can do this because convex optimized = False while not optimized: for b in np.arange(-1*(self.max_feature_value*b_range_multiple), self.max_feature_value*b_range_multiple, step*b_multiple): for transformation in transforms: w_t = w*transformation found_option = True # weakest link in the SVM fundamentally # SMO attempts to fix this a bit # yi(xi.w+b) >= 1 # # #### add a break here later.. for i in self.data: for xi in self.data[i]: yi=i if not yi*(np.dot(w_t,xi)+b) >= 1: found_option = False if found_option: opt_dict[np.linalg.norm(w_t)] = [w_t,b] if w[0] < 0: optimized = True print('Optimized a step.') else: w = w - step norms = sorted([n for n in opt_dict]) #||w|| : [w,b] opt_choice = opt_dict[norms[0]] self.w = opt_choice[0] self.b = opt_choice[1] latest_optimum = opt_choice[0][0]+step*2 def predict(self,features): # sign( x.w+b ) classification = np.sign(np.dot(np.array(features),self.w)+self.b) return classification data_dict = {-1:np.array([[1,7], [2,8], [3,8],]), 1:np.array([[5,1], [6,-1], [7,3],])} ``` 我們已經擁有預測方法了，因為這非常簡單。但是現在我們打算添加一些，來處理預測的可視化。 ```py def predict(self,features): # classifiction is just: # sign(xi.w+b) classification = np.sign(np.dot(np.array(features),self.w)+self.b) # if the classification isn't zero, and we have visualization on, we graph if classification != 0 and self.visualization: self.ax.scatter(features[0],features[1],s=200,marker='*', c=self.colors[classification]) else: print('featureset',features,'is on the decision boundary') return classification ``` 上面，我們添加了代碼來可視化預測，如果存在的話。我們打算一次做一個，但是你可以擴展代碼來一次做許多個，就像 Sklearn 那樣。 下面，讓我們構建`visualize`方法： ```py def visualize(self): #scattering known featuresets. [[self.ax.scatter(x[0],x[1],s=100,color=self.colors[i]) for x in data_dict[i]] for i in data_dict] ``` 這一行所做的就是，遍歷我們的數據，并繪制它和它的相應顏色。 下面，我們打算繪制正向和負向支持向量的超平面，以及決策邊界。為此，我們至少需要兩個點，來創建“直線”，它就是我們的超平面。 一旦我們知道了`w`和`b`，我們就可以使用代數來創建函數，它對`x`值返回`y`值來生成直線： ```py def hyperplane(x,w,b,v): # w[0] * x + w[1] * y + b = v # 正向支持超平面 v = 1 # 最佳分隔超平面 v = 0 # 負向支持超平面 v = -1 # y = (v - b - w[0] * x) / w[1] return (-w[0]*x-b+v) / w[1] ``` 然后，我們創建一些變量，來存放我們打算引用的多種數據： ```py datarange = (self.min_feature_value*0.9,self.max_feature_value*1.1) hyp_x_min = datarange[0] hyp_x_max = datarange[1] ``` 我們的主要目標就是弄清楚為了繪制我們的超平面，我們需要什么值。 現在，讓我們繪制正向支持向量超平面。 ```py # w.x + b = 1 # pos sv hyperplane psv1 = hyperplane(hyp_x_min, self.w, self.b, 1) psv2 = hyperplane(hyp_x_max, self.w, self.b, 1) self.ax.plot([hyp_x_min,hyp_x_max], [psv1,psv2], "k") ``` 非常簡單，我們獲得了`x_min`和`x_max`的`y`值，然后我們繪制了它們。 ··· # w.x + b = -1 # negative sv hyperplane nsv1 = hyperplane(hyp_x_min, self.w, self.b, -1) nsv2 = hyperplane(hyp_x_max, self.w, self.b, -1) self.ax.plot([hyp_x_min,hyp_x_max], [nsv1,nsv2], "k") # w.x + b = 0 # decision db1 = hyperplane(hyp_x_min, self.w, self.b, 0) db2 = hyperplane(hyp_x_max, self.w, self.b, 0) self.ax.plot([hyp_x_min,hyp_x_max], [db1,db2], "g--") plt.show() ``` 現在，在底部添加一些代碼來訓練、預測和可視化： ```py import matplotlib.pyplot as plt from matplotlib import style import numpy as np style.use('ggplot') class Support_Vector_Machine: def __init__(self, visualization=True): self.visualization = visualization self.colors = {1:'r',-1:'b'} if self.visualization: self.fig = plt.figure() self.ax = self.fig.add_subplot(1,1,1) # train def fit(self, data): self.data = data # { ||w||: [w,b] } opt_dict = {} transforms = [[1,1], [-1,1], [-1,-1], [1,-1]] all_data = [] for yi in self.data: for featureset in self.data[yi]: for feature in featureset: all_data.append(feature) self.max_feature_value = max(all_data) self.min_feature_value = min(all_data) all_data = None # support vectors yi(xi.w+b) = 1 step_sizes = [self.max_feature_value * 0.1, self.max_feature_value * 0.01, # point of expense: self.max_feature_value * 0.001, ] # extremely expensive b_range_multiple = 2 # we dont need to take as small of steps # with b as we do w b_multiple = 5 latest_optimum = self.max_feature_value*10 for step in step_sizes: w = np.array([latest_optimum,latest_optimum]) # we can do this because convex optimized = False while not optimized: for b in np.arange(-1*(self.max_feature_value*b_range_multiple), self.max_feature_value*b_range_multiple, step*b_multiple): for transformation in transforms: w_t = w*transformation found_option = True # weakest link in the SVM fundamentally # SMO attempts to fix this a bit # yi(xi.w+b) >= 1 # # #### add a break here later.. for i in self.data: for xi in self.data[i]: yi=i if not yi*(np.dot(w_t,xi)+b) >= 1: found_option = False #print(xi,':',yi*(np.dot(w_t,xi)+b)) if found_option: opt_dict[np.linalg.norm(w_t)] = [w_t,b] if w[0] < 0: optimized = True print('Optimized a step.') else: w = w - step norms = sorted([n for n in opt_dict]) #||w|| : [w,b] opt_choice = opt_dict[norms[0]] self.w = opt_choice[0] self.b = opt_choice[1] latest_optimum = opt_choice[0][0]+step*2 for i in self.data: for xi in self.data[i]: yi=i print(xi,':',yi*(np.dot(self.w,xi)+self.b)) def predict(self,features): # sign( x.w+b ) classification = np.sign(np.dot(np.array(features),self.w)+self.b) if classification !=0 and self.visualization: self.ax.scatter(features[0], features[1], s=200, marker='*', c=self.colors[classification]) return classification def visualize(self): [[self.ax.scatter(x[0],x[1],s=100,color=self.colors[i]) for x in data_dict[i]] for i in data_dict] # hyperplane = x.w+b # v = x.w+b # psv = 1 # nsv = -1 # dec = 0 def hyperplane(x,w,b,v): return (-w[0]*x-b+v) / w[1] datarange = (self.min_feature_value*0.9,self.max_feature_value*1.1) hyp_x_min = datarange[0] hyp_x_max = datarange[1] # (w.x+b) = 1 # positive support vector hyperplane psv1 = hyperplane(hyp_x_min, self.w, self.b, 1) psv2 = hyperplane(hyp_x_max, self.w, self.b, 1) self.ax.plot([hyp_x_min,hyp_x_max],[psv1,psv2], 'k') # (w.x+b) = -1 # negative support vector hyperplane nsv1 = hyperplane(hyp_x_min, self.w, self.b, -1) nsv2 = hyperplane(hyp_x_max, self.w, self.b, -1) self.ax.plot([hyp_x_min,hyp_x_max],[nsv1,nsv2], 'k') # (w.x+b) = 0 # positive support vector hyperplane db1 = hyperplane(hyp_x_min, self.w, self.b, 0) db2 = hyperplane(hyp_x_max, self.w, self.b, 0) self.ax.plot([hyp_x_min,hyp_x_max],[db1,db2], 'y--') plt.show() data_dict = {-1:np.array([[1,7], [2,8], [3,8],]), 1:np.array([[5,1], [6,-1], [7,3],])} svm = Support_Vector_Machine() svm.fit(data=data_dict) predict_us = [[0,10], [1,3], [3,4], [3,5], [5,5], [5,6], [6,-5], [5,8]] for p in predict_us: svm.predict(p) 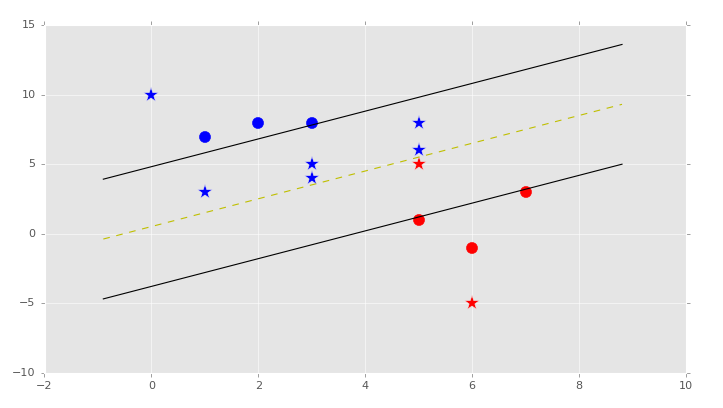svm.visualize() ``` 我們的結果：  ## 二十九、核的簡介 歡迎閱讀第二十九篇教程。這個教程中，我們打算使用機器學習談論核的概念。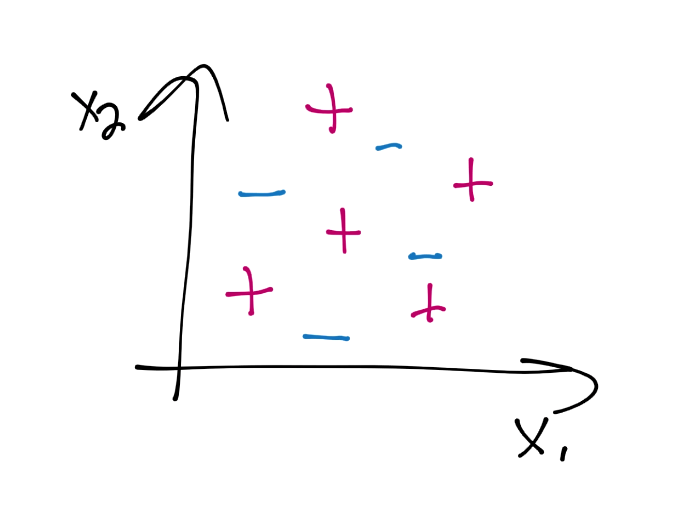 回憶一開始的 SVM 話題，我們的問題是，你可不可以使用 SVM 來處理這樣的數據：  至少我們現在為止，它可能嗎？不，完全不可能，至少不能是這樣。但是一個選擇，就是采取新的視角。我們可以通過添加一個新的維度來實現。例如上面的數據中，我們可以添加第三個維度，使用一些函數，比如`X3 = X1*X2`。在這里可能管用，但是也可以不管用。同樣，一些案例，比如圖像分析又如何呢？其中你可能有多于幾百和維度。它就是性能很重要的場景，并且你是否應該添加一個維度到已經有很多維度的數據中，我們會進一步把事情變慢。 如果我告訴你，你可以在無限的維度上做計算，或者，你可以讓那些計算在這些維度上實現，而不需要在這些維度上工作，并且仍然能得到結果呢？ 就是這樣。我們實際上使用叫做核的東西來實現。相對于 SVM 來說，許多人一開始就接觸它了，也可能最后才接觸。這可能會讓你認為，核主要用于 SVM，但是并不是這樣。 核就是相似度函數，它接受兩個輸出，并使用內積來返回相似度。由于這是個機器學習教程，你們中的一些可能想知道，為什么人們不將核用于機器學習算，以及，我在這里告訴你它們實際上使用了。你不僅僅可以使用核來創建自己的機器學習算法，你可以將現有的機器學習算法翻譯為使用核的版本。 核所做的就是允許你，處理許多維度，而不需要花費處理的開銷。核的確有個要求：它們依賴于內核。對于這篇教程的目的，“點積”和“內積”可以互相代替。 為了驗證我們是否可以使用核，我們需要做的，就是驗證我們的特征空間的每個交互，都是內積。我們會從末尾開始，然后返回來確認它。 首先，我們如何在訓練之后判斷特征的分類呢？  它是不是內積的交互呢？當然是，我們可以將`x`換成`z`。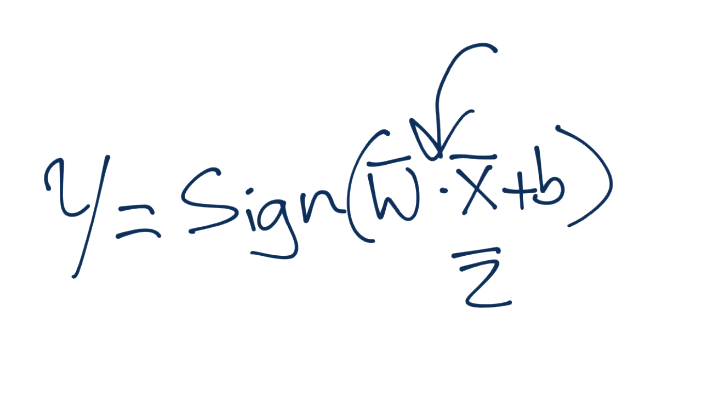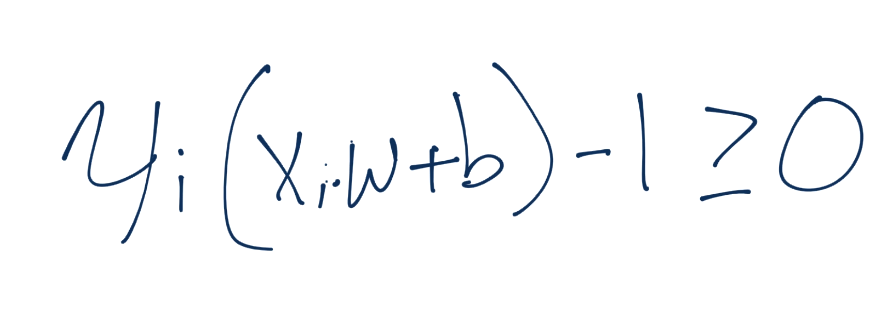  繼續，我們打算回顧我們的約束，約束方程為：  這里如何呢？這個交互式內積嘛？當然，` yi(xi.w+b)-1 >= 0`等價于`yi(xi.w+b) >= 1`。所以這里我們可以講義將`x_i`替換為`z_i`。 最后，我們的形式優化方程`w`如何呢？  它是另一個點積或內積。有任何問題嗎？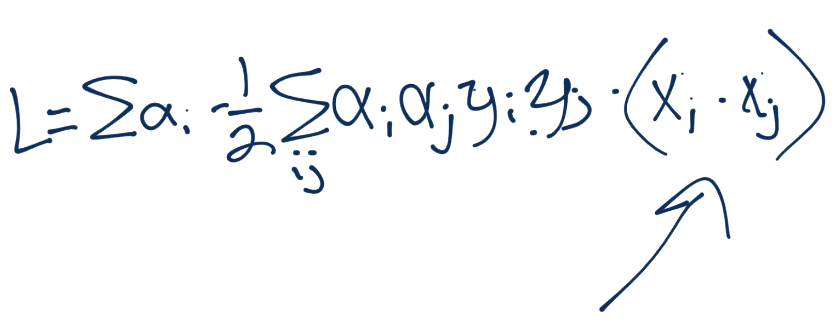這樣：  太好了。我們可以使用核。你可能想知道，這個“零開銷來計算無窮維度”是什么？好吧，首先我們需要確保我們能這樣做。對于零開銷的處理，你需要看下一篇教程來了解。 ## 三十、為什么是核 歡迎閱讀第三十篇教程。這篇教程中，我們打算繼續討論核，既然我們知道了我們能使用它之后，主要弄清楚如何實際使用它們。 我們之前了解到，我們可以利用核來幫助我們將數據轉換為無窮數量的維度，以便找到線性分隔。我們也了解到，核可以讓我們處理這些維度，而不需要實際為這些高維度花費開銷。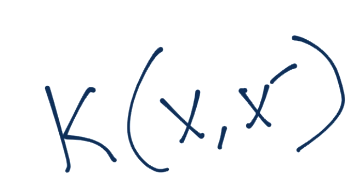通常，核定義為這樣：  核函數應用于`x`和`x'`，并等于`z`和`z'`的內積，其中`z`就是`z`維度的值（我們新的維度空間）。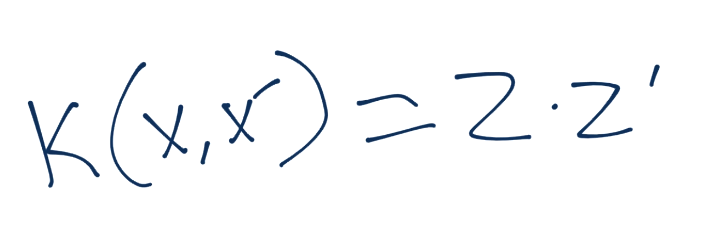  `z`值就是一些`function(x)`的結果，這些`z`值點乘在一起就是我們核函數的結果。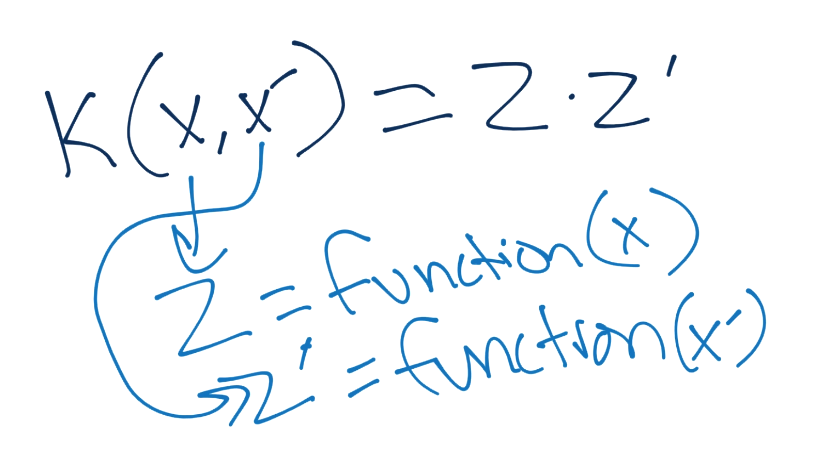  我們仍然需要涉及，它如何節省我們的處理步驟。所以看一個例子吧。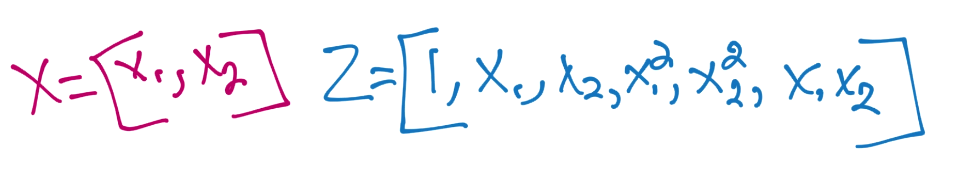我們以多項式來開始，并將多項式核的要求，與簡單使用我們的向量來創建二階多項式來比較：  核對`x`和`x'`使用相同函數，所以我們對`z'`也使用相同的東西（`x'`對二階多項式）。這里，最終步驟就是計算二者的點積。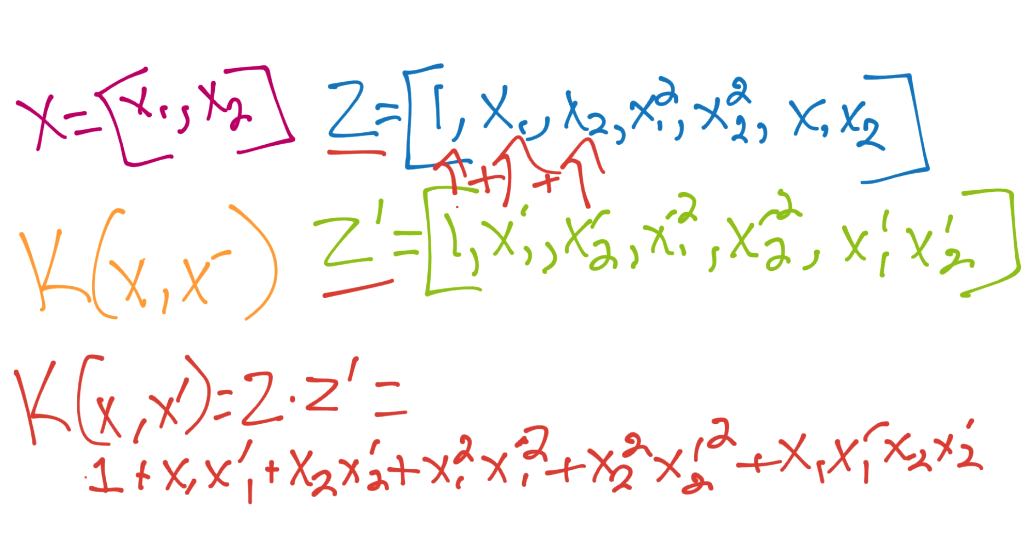  所以所有工作就是手動執行一個和核函數類似的操作。幸運的是，我們的起始維度只有兩維。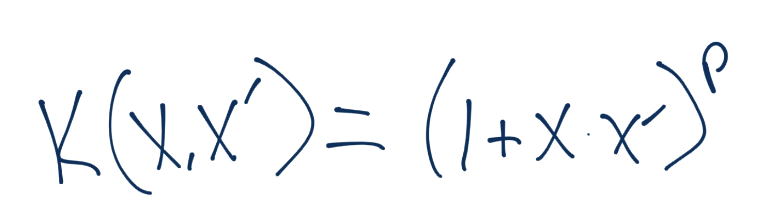現在讓我們考慮多項式核：  要注意，這里沒有提到`z`。整個核僅僅使用`x`來計算。你所需的所有東西，就是使用維度數量`n`和你想使用的權重`p`來計算。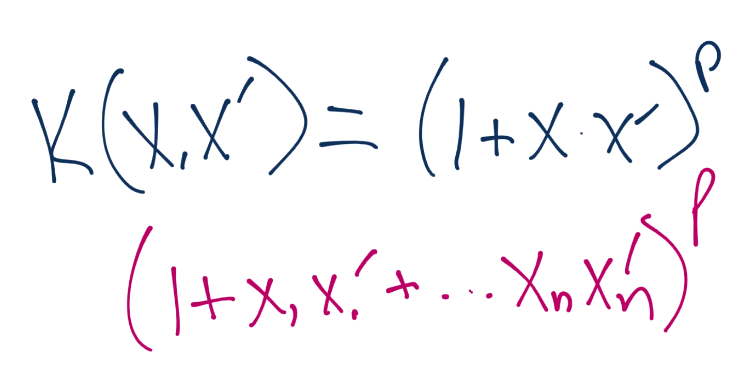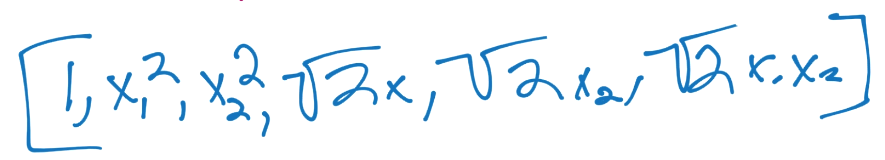你的方程是這樣：  如果你計算了出來，你的新向量是這樣，它對應`z`空間的向量：  也就是說，你永遠不需要繼續深入了。你只需要專注于多項式和，它簡單返回點積給你，你不需要實際計算向量，之后計算非常大的點積。 也有一些預先創建的核，但是我這里僅僅會展示徑向基函數（RBF）核。只是因為它通常是默認使用的核，并且可以將我們帶到無限的維度中。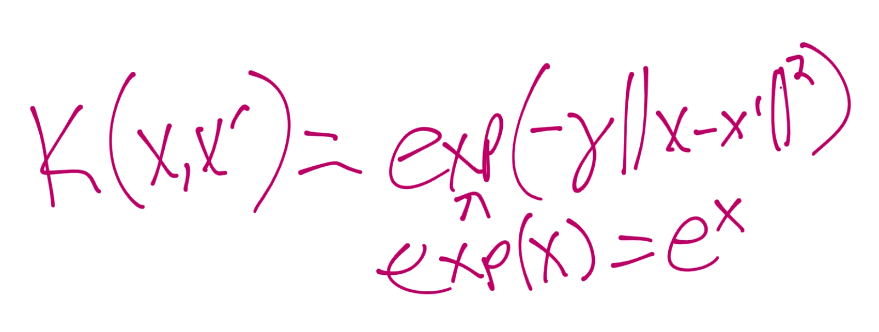  這里的 Gamma 值是后面教程的話題。所以這里以擁有了核，了解了為什么使用它們，如何使用它們，以及它們如何讓你處理更大的維度，而不需要花費非常大的處理開銷。下一篇教程中，我們打算討論另一個非線性數據的解決方案，以及數據的過擬合問題。 ## 三十一、軟邊界 SVM 歡迎閱讀第 31 個部分。這篇教程中，我們打算討論軟邊界 SVM。 首先，為什么軟邊界分類器更加優秀，主要有兩個原因。一是你的數據可能不是完全線性分隔的，但是很接近了，并且繼續使用默認的線性核有更大意義。另一個原因是，即使你使用了某個核，如果你打算使用硬邊界的話，你最后也會過擬合。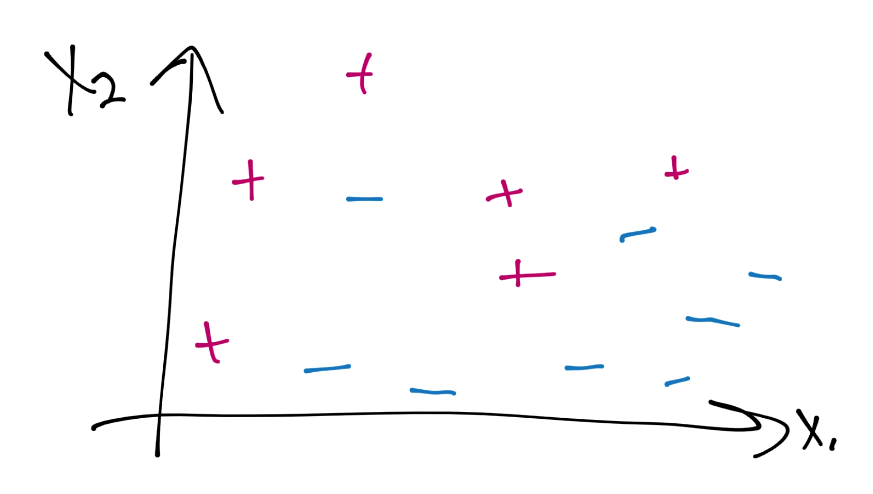例如，考慮這個：  這里是一個數據案例，當前并不是線性可分的。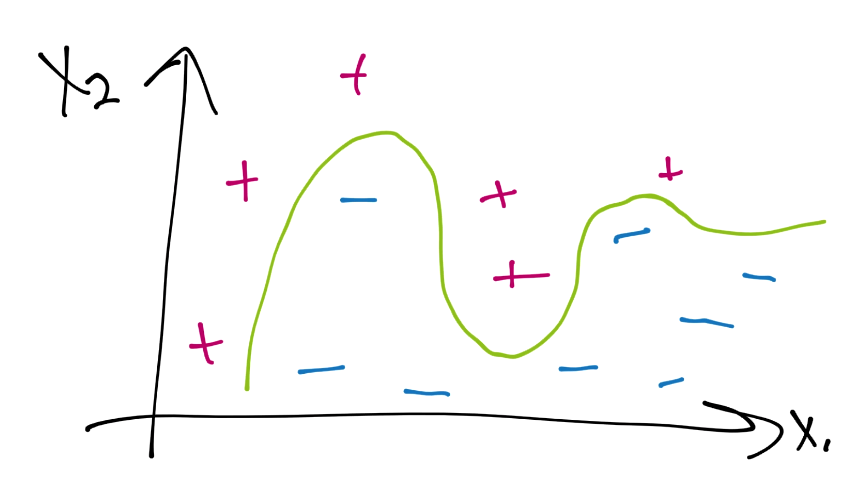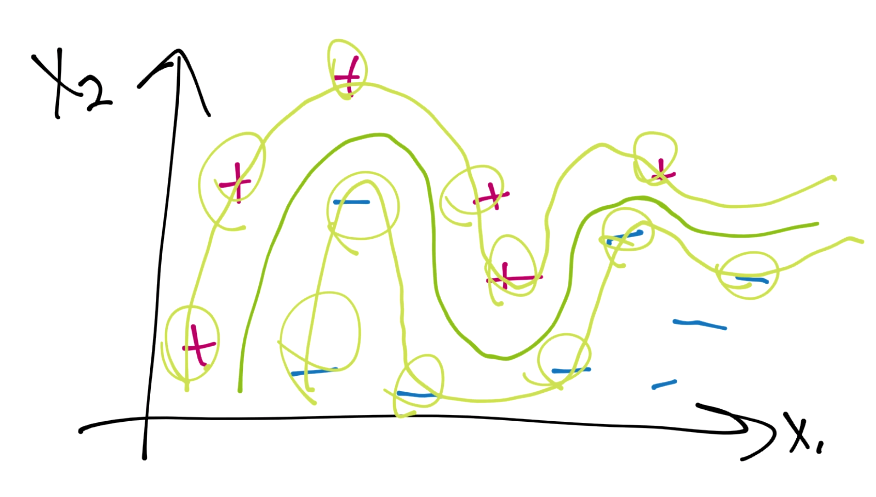假設使用硬邊界（也就是我們之前看到的那種），我們可能使用核來生成這樣的決策邊界：  下面，注意我的繪圖工具中的缺陷，讓我們繪制支持向量平面，并圈出支持向量：  這里，每個正向的數據樣例都是支持向量，只有兩個負向分類不是支持向量。這個信號就是可能過擬合了，我們應該避免它。因為，當我們用它來預測未來的點時，我們就沒有余地了，并且可能會錯誤分類新的數據。如果我們這樣做，會怎么樣呢？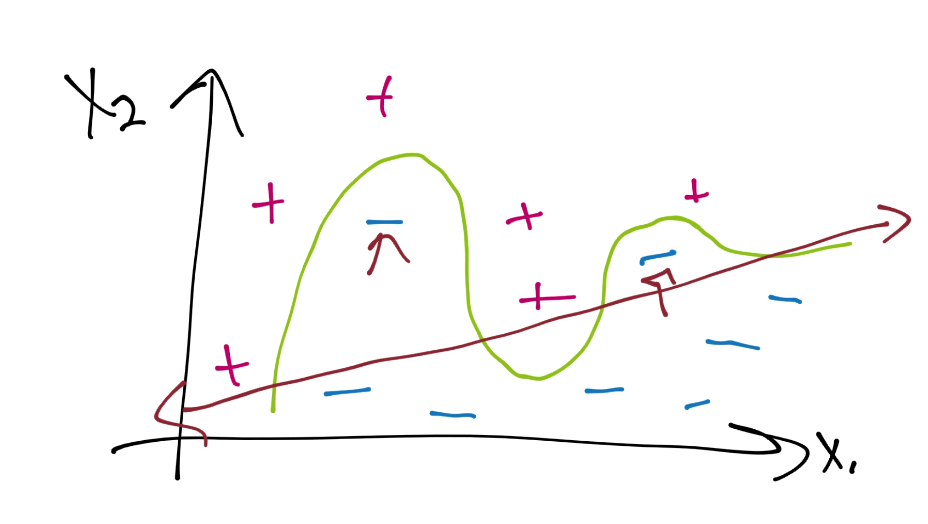  我們有一些錯誤或者誤差，由箭頭標記，但是這個可能能夠更好地為將來的數據集分類。我們這里就擁有了“軟邊界”分類器，它允許一些誤差上的“彈性”，我們可以在優化過程中獲得它。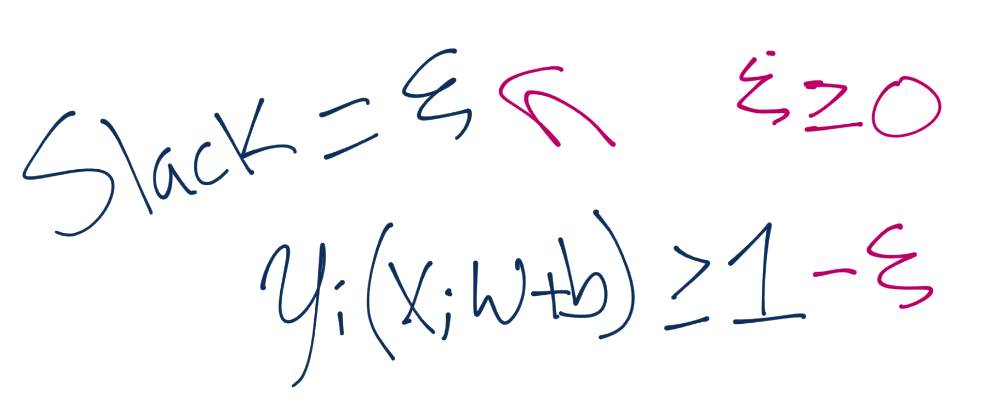  我們的新的優化就是上面的計算，其中彈性大于等于 0。彈性越接近 0，就越接近“硬邊界”。彈性越高，邊界就越軟。如果彈性是 0，我們就得到了一個典型的硬邊界分類器。但是你可能能夠菜刀，我們希望最小化彈性。為此，我們將其添加到向量`w`的模的最小值中。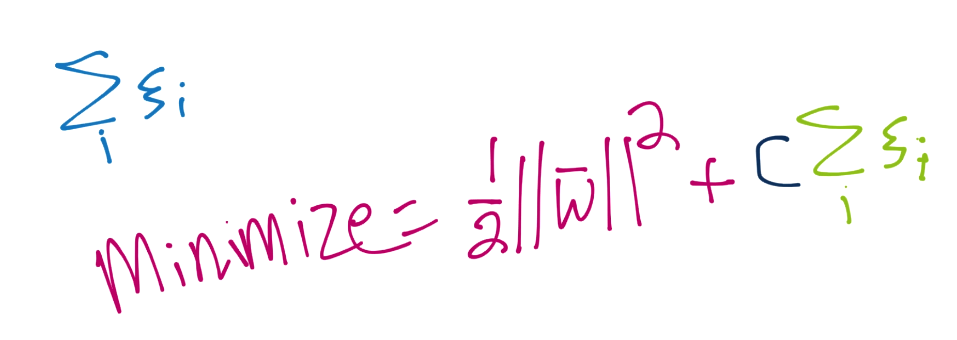  因此，我們實際上打算最小化`1/2||w||^2 + C * 所有使用的彈性之和`。使用它，我們引入了另一個變量`C`。`C`是個系數，關于我們打算讓彈性對方程的剩余部分有多少影響。`C`閱讀，彈性的和與向量`w`的模相比，就越不重要，反之亦然。多數情況下，`C`的值默認為 1。 所以這里你了解了軟邊界 SVM，以及為什么打算使用它。下面，我們打算展示一些樣例代碼，它們由軟邊界、核和 CVXOPT 組成。 ## 三十二、核、軟邊界和使用 Python 和 CVXOPT 的平方規劃 歡迎閱讀第三十二篇機器學習教程。這篇教程中，我們打算展示核、軟邊界的 Python 版本，并使用 CVXOPT 來解決平方規劃問題。 在這個簡短的章節中，我打算主要向你分享其它資源，你應該想要使用 Python 和 CVXOPT 深入研究 SVM 或者平方規劃。為了開始，你可以閱讀[ CVXOPT 平方規劃文檔](https://cvxopt.org/userguide/coneprog.html#quadratic-programming)，來深入了解 Python 中的平方規劃。你也可以查看[ CVXOPT 平方規劃示例](https://cvxopt.org/examples/tutorial/qp.html)。 對于 CVXOPT 的更加深入的平方規劃示例，請查看[這個 PDF](https://courses.csail.mit.edu/6.867/wiki/images/a/a7/Qp-cvxopt.pdf)。 最后，我們打算看一看來自[ Mathieu Blondel 的博客](http://www.mblondel.org/journal/2010/09/19/support-vector-machines-in-python/)的一些代碼，它由核、軟邊界 SVM 以及 CVXOPT 平方規劃組成。所有代碼都優于我寫的任何東西。 ```py # Mathieu Blondel, September 2010 # License: BSD 3 clause # http://www.mblondel.org/journal/2010/09/19/support-vector-machines-in-python/ # visualizing what translating to another dimension does # and bringing back to 2D: # https://www.youtube.com/watch?v=3liCbRZPrZA # Docs: http://cvxopt.org/userguide/coneprog.html#quadratic-programming # Docs qp example: http://cvxopt.org/examples/tutorial/qp.html # Nice tutorial: # https://courses.csail.mit.edu/6.867/wiki/images/a/a7/Qp-cvxopt.pdf import numpy as np from numpy import linalg import cvxopt import cvxopt.solvers def linear_kernel(x1, x2): return np.dot(x1, x2) def polynomial_kernel(x, y, p=3): return (1 + np.dot(x, y)) ** p def gaussian_kernel(x, y, sigma=5.0): return np.exp(-linalg.norm(x-y)**2 / (2 * (sigma ** 2))) class SVM(object): def __init__(self, kernel=linear_kernel, C=None): self.kernel = kernel self.C = C if self.C is not None: self.C = float(self.C) def fit(self, X, y): n_samples, n_features = X.shape # Gram matrix K = np.zeros((n_samples, n_samples)) for i in range(n_samples): for j in range(n_samples): K[i,j] = self.kernel(X[i], X[j]) P = cvxopt.matrix(np.outer(y,y) * K) q = cvxopt.matrix(np.ones(n_samples) * -1) A = cvxopt.matrix(y, (1,n_samples)) b = cvxopt.matrix(0.0) if self.C is None: G = cvxopt.matrix(np.diag(np.ones(n_samples) * -1)) h = cvxopt.matrix(np.zeros(n_samples)) else: tmp1 = np.diag(np.ones(n_samples) * -1) tmp2 = np.identity(n_samples) G = cvxopt.matrix(np.vstack((tmp1, tmp2))) tmp1 = np.zeros(n_samples) tmp2 = np.ones(n_samples) * self.C h = cvxopt.matrix(np.hstack((tmp1, tmp2))) # solve QP problem solution = cvxopt.solvers.qp(P, q, G, h, A, b) # Lagrange multipliers a = np.ravel(solution['x']) # Support vectors have non zero lagrange multipliers sv = a > 1e-5 ind = np.arange(len(a))[sv] self.a = a[sv] self.sv = X[sv] self.sv_y = y[sv] print("%d support vectors out of %d points" % (len(self.a), n_samples)) # Intercept self.b = 0 for n in range(len(self.a)): self.b += self.sv_y[n] self.b -= np.sum(self.a * self.sv_y * K[ind[n],sv]) self.b /= len(self.a) # Weight vector if self.kernel == linear_kernel: self.w = np.zeros(n_features) for n in range(len(self.a)): self.w += self.a[n] * self.sv_y[n] * self.sv[n] else: self.w = None def project(self, X): if self.w is not None: return np.dot(X, self.w) + self.b else: y_predict = np.zeros(len(X)) for i in range(len(X)): s = 0 for a, sv_y, sv in zip(self.a, self.sv_y, self.sv): s += a * sv_y * self.kernel(X[i], sv) y_predict[i] = s return y_predict + self.b def predict(self, X): return np.sign(self.project(X)) if __name__ == "__main__": import pylab as pl def gen_lin_separable_data(): # generate training data in the 2-d case mean1 = np.array([0, 2]) mean2 = np.array([2, 0]) cov = np.array([[0.8, 0.6], [0.6, 0.8]]) X1 = np.random.multivariate_normal(mean1, cov, 100) y1 = np.ones(len(X1)) X2 = np.random.multivariate_normal(mean2, cov, 100) y2 = np.ones(len(X2)) * -1 return X1, y1, X2, y2 def gen_non_lin_separable_data(): mean1 = [-1, 2] mean2 = [1, -1] mean3 = [4, -4] mean4 = [-4, 4] cov = [[1.0,0.8], [0.8, 1.0]] X1 = np.random.multivariate_normal(mean1, cov, 50) X1 = np.vstack((X1, np.random.multivariate_normal(mean3, cov, 50))) y1 = np.ones(len(X1)) X2 = np.random.multivariate_normal(mean2, cov, 50) X2 = np.vstack((X2, np.random.multivariate_normal(mean4, cov, 50))) y2 = np.ones(len(X2)) * -1 return X1, y1, X2, y2 def gen_lin_separable_overlap_data(): # generate training data in the 2-d case mean1 = np.array([0, 2]) mean2 = np.array([2, 0]) cov = np.array([[1.5, 1.0], [1.0, 1.5]]) X1 = np.random.multivariate_normal(mean1, cov, 100) y1 = np.ones(len(X1)) X2 = np.random.multivariate_normal(mean2, cov, 100) y2 = np.ones(len(X2)) * -1 return X1, y1, X2, y2 def split_train(X1, y1, X2, y2): X1_train = X1[:90] y1_train = y1[:90] X2_train = X2[:90] y2_train = y2[:90] X_train = np.vstack((X1_train, X2_train)) y_train = np.hstack((y1_train, y2_train)) return X_train, y_train def split_test(X1, y1, X2, y2): X1_test = X1[90:] y1_test = y1[90:] X2_test = X2[90:] y2_test = y2[90:] X_test = np.vstack((X1_test, X2_test)) y_test = np.hstack((y1_test, y2_test)) return X_test, y_test def plot_margin(X1_train, X2_train, clf): def f(x, w, b, c=0): # given x, return y such that [x,y] in on the line # w.x + b = c return (-w[0] * x - b + c) / w[1] pl.plot(X1_train[:,0], X1_train[:,1], "ro") pl.plot(X2_train[:,0], X2_train[:,1], "bo") pl.scatter(clf.sv[:,0], clf.sv[:,1], s=100, c="g") # w.x + b = 0 a0 = -4; a1 = f(a0, clf.w, clf.b) b0 = 4; b1 = f(b0, clf.w, clf.b) pl.plot([a0,b0], [a1,b1], "k") # w.x + b = 1 a0 = -4; a1 = f(a0, clf.w, clf.b, 1) b0 = 4; b1 = f(b0, clf.w, clf.b, 1) pl.plot([a0,b0], [a1,b1], "k--") # w.x + b = -1 a0 = -4; a1 = f(a0, clf.w, clf.b, -1) b0 = 4; b1 = f(b0, clf.w, clf.b, -1) pl.plot([a0,b0], [a1,b1], "k--") pl.axis("tight") pl.show() def plot_contour(X1_train, X2_train, clf): pl.plot(X1_train[:,0], X1_train[:,1], "ro") pl.plot(X2_train[:,0], X2_train[:,1], "bo") pl.scatter(clf.sv[:,0], clf.sv[:,1], s=100, c="g") X1, X2 = np.meshgrid(np.linspace(-6,6,50), np.linspace(-6,6,50)) X = np.array([[x1, x2] for x1, x2 in zip(np.ravel(X1), np.ravel(X2))]) Z = clf.project(X).reshape(X1.shape) pl.contour(X1, X2, Z, [0.0], colors='k', linewidths=1, origin='lower') pl.contour(X1, X2, Z + 1, [0.0], colors='grey', linewidths=1, origin='lower') pl.contour(X1, X2, Z - 1, [0.0], colors='grey', linewidths=1, origin='lower') pl.axis("tight") pl.show() def test_linear(): X1, y1, X2, y2 = gen_lin_separable_data() X_train, y_train = split_train(X1, y1, X2, y2) X_test, y_test = split_test(X1, y1, X2, y2) clf = SVM() clf.fit(X_train, y_train) y_predict = clf.predict(X_test) correct = np.sum(y_predict == y_test) print("%d out of %d predictions correct" % (correct, len(y_predict))) plot_margin(X_train[y_train==1], X_train[y_train==-1], clf) def test_non_linear(): X1, y1, X2, y2 = gen_non_lin_separable_data() X_train, y_train = split_train(X1, y1, X2, y2) X_test, y_test = split_test(X1, y1, X2, y2) clf = SVM(polynomial_kernel) clf.fit(X_train, y_train) y_predict = clf.predict(X_test) correct = np.sum(y_predict == y_test) print("%d out of %d predictions correct" % (correct, len(y_predict))) plot_contour(X_train[y_train==1], X_train[y_train==-1], clf) def test_soft(): X1, y1, X2, y2 = gen_lin_separable_overlap_data() X_train, y_train = split_train(X1, y1, X2, y2) X_test, y_test = split_test(X1, y1, X2, y2) clf = SVM(C=1000.1) clf.fit(X_train, y_train) y_predict = clf.predict(X_test) correct = np.sum(y_predict == y_test) print("%d out of %d predictions correct" % (correct, len(y_predict))) plot_contour(X_train[y_train==1], X_train[y_train==-1], clf) #test_linear() #test_non_linear() test_soft() ``` 如果你想要讓我執行這個代碼，你可以查看[這個視頻](https://www.youtube.com/embed/XdcfJX-mDG4?list=PLQVvvaa0QuDfKTOs3Keq_kaG2P55YRn5v)。我會僅僅提及，你可能不需要使用 CVXOPT。多數人用于 SVM 的庫是[ LibSVM](https://www.csie.ntu.edu.tw/~cjlin/libsvm/)。 大家都說，這個代碼可以讓你理解內部的工作原理，并不是為了讓你實際創建一個健壯的 SVM，超過你可以自由使用的那個。 下一篇教程中，我們打算再討論一個 SVM 的概念，它就是當你擁有多于兩個分組時，你該怎么做。我們也會在總結中，瀏覽 Sklearn 的 SVM 的所有參數，因為我們很少涉及這個話題。 # 第三十三章 支持向量機的參數 > 原文：[Support Vector Machine Parameters](https://pythonprogramming.net/support-vector-machine-parameters-machine-learning-tutorial/) > 譯者：[飛龍](https://github.com/wizardforcel) > 協議：[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/) 歡迎閱讀第三十三篇教程，這篇教程中，我們打算通過解釋如何處理多于 2 個分類，以及盧蘭 Sklearn 的 SVM 的參數，來對 SVM 做個收尾，并且讓你見識一下用于 SVM 的現代方法論。 首先，你已經學到了，SVM 是個二元分類器。也就是說，任何時候，SVM 的最優化都只能將一個分組與另一個分組分離。之后問題是我們如何對三個或更多分組分類。通常，方法就是“一對其它”（OVR）。這里的理念就是，將每個分組從其余的分組分離。例如，為了分類三個分組（1，2 和 3），你應該首先將 1 從 2 和 3 分離。之后將 2 從 1 和 3。最后將 3 從 1 和 2 分離。這樣有一些問題，因為類似置信度的東西，可能對于每個分類邊界都不同，以及分隔邊界可能有一些缺陷，因為有一些不僅僅是正向和負向的東西，你將一個分組與其它三個比較。假設最開始有一個均衡的數據集，也就是說每個分類的邊界可能是不均衡的。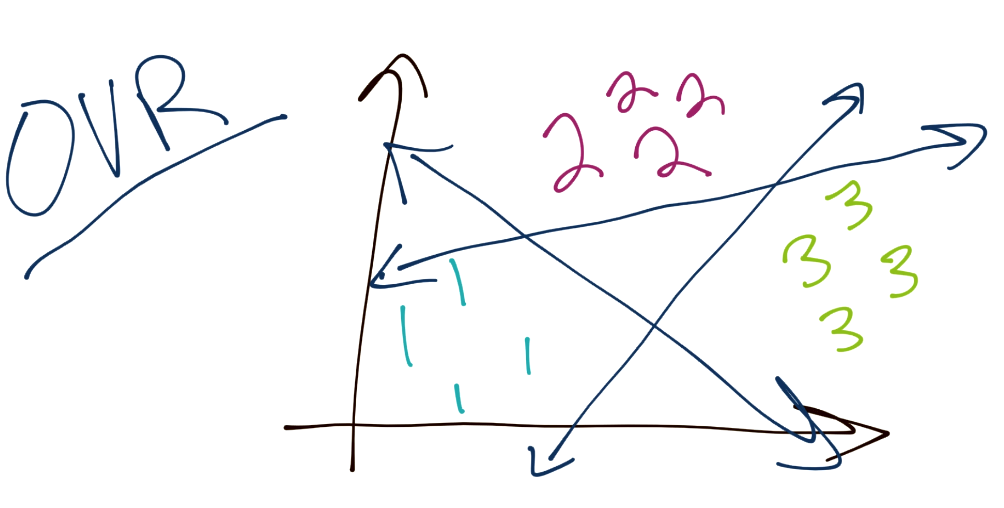  另一個方法是“一對一”（OVO）。這個情況下，考慮你總共擁有三個分組。它的工作方式是，你的邊界從 1 分離 3，以及從 1 分離 2，并且對其余分類重復這個過程。這樣，邊界就會更均衡。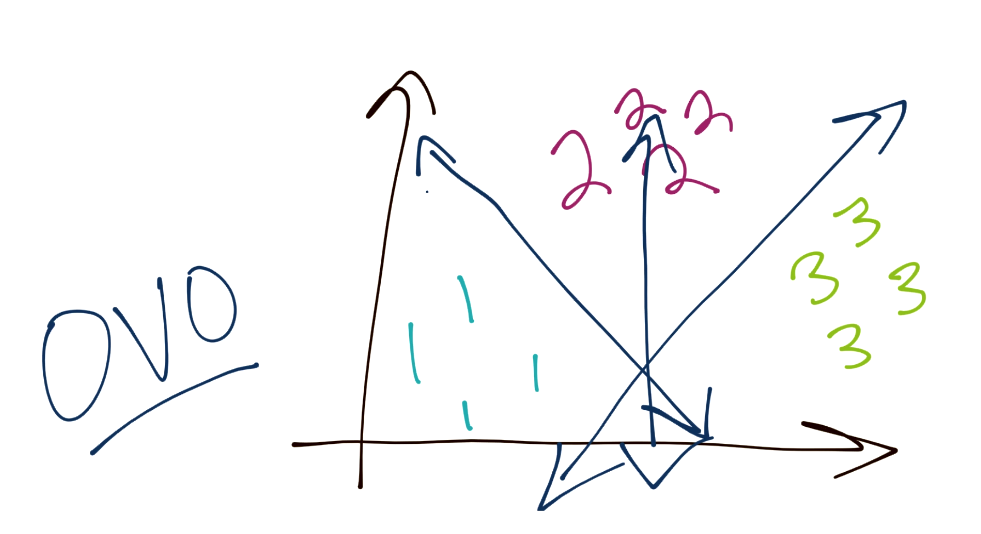  第一個參數是`C`。它告訴你這是一個軟邊界分類器。你可以按需調整`C`，并且可以使`C`足夠高來創建硬邊界分類器。`C`是`||w||`的軟邊界優化函數。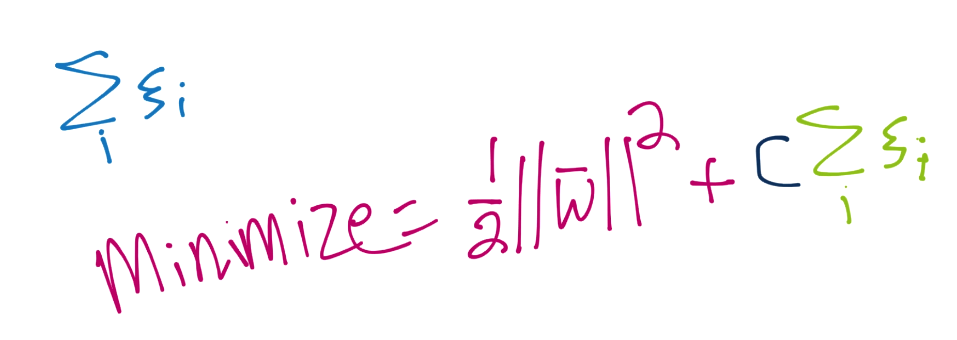  `C`的默認值是 1，并且多數情況下都很好。 下面我們有個`kernel`的選項。這里默認是`rbf`核，但是你可以調整為`linear`，`poly`（多項式）和`sigmoid`核，甚至你選擇或設計的自定義核。 然后，還有`degree`值，默認為 3，這個是多項式的階數，如果你將`poly`用于`kernel`參數的話。 `gamma`是你為`rbf`核設置 Gamma 值的地方。你應該將其保留為`auto`。 `coef0`允許你調整核函數的獨立項，但是你應該保留不變，并且它只用于多項式和 sigmoid 核。 `probability `參數項可能對你很使用。回憶 KNN 算法不僅僅擁有模型準確度，每個預測還擁有置信度。SVM 本質上沒有這個屬性，但是你可以使用`probability `參數來獲取一種形式。這是個開銷大的功能，但是可能對你來說足夠重要，或者默認值為`False`。 下面是`shrinking`布爾值，它默認為`True`。這個用于表示你是否將啟發式用于 SVM 的優化，它使用了序列最小優化（SMO）。你應該將其保留為`True`，因為它可以極大提升你的性能，并且只損失一點點準確性。 `tol`參數設置了 SVM 的容差。前面說過`yi(xi.w+b)-1 >= 0`。對于 SVM 來說，所有值都必須大于等于 0，每一邊至少一個值要等于 0，這就是你的支持向量。由于你不可能讓值（浮點數）完全等于 0，你需要設置一個容差來獲取一些彈性空間。Sklearn 中默認的 `tol`是`1e-3`，也就是 0.001。 下一個重要的參數是`max_iter`，它是你可以為平方規劃設置最大迭代次數的地方。默認值為`-1`，也就是沒有限制。 `decision_function_shape `是一對一（OVO），或者一對其它（OVR），那就是教程開始討論的概念。 `random_state `用于概率估計中的種子，如果你打算指定的話。 除了這些參數，我們還有幾個屬性。 `support_ `提供了支持向量的索引。`support_vectors_ `提供了實際的支持向量。`n_support_`是支持向量的個數，如果你的數據集有一些統計問題，將它與你的數據集尺寸相比非常實用。最后三個參數是`dual_coef_`、` coef_`和`intercept_`，如果你打算繪制 SVM，會非常實用。 SVM 就講完了。下一個話題是聚類。