# 使用orange進行聚類分析 小麥籽粒幾何性狀的測定 ## 知識點 - 數據的預處理 - Orange 數據集的格式 - 數據分布的含義 - 特征排序 - ## 實驗過程 ### 數據集 種子數據集：https://archive.ics.uci.edu/ml/datasets/seeds > 以下鏈接下載的文件是一個txt文件，使用TAB格式分隔的，數據需要簡單的處理以下才能正常使用。 https://archive.ics.uci.edu/ml/machine-learning-databases/00236/seeds_dataset.txt 處理完的實驗數據集，在課程資源包中提供，并做了漢化。 ??? 三種不同品種小麥籽粒幾何性狀的測定。用于軟X射線技術和GRAINS構建七個實值屬性，所有這些參數都是實值連續的。 ??? 1、面積A，? ??? 2、周長P，? ??? 3、緊湊度C = 4 * pi * A / P ^ 2,4? ??? 4、籽粒長度，? ??? 5、籽粒寬度，? ??? 6、不對稱系數? ??? 7、核槽的長度。? ??? 下載數據的文件格式為.txt格式，將文件格式改為.csv或.xlsx格式。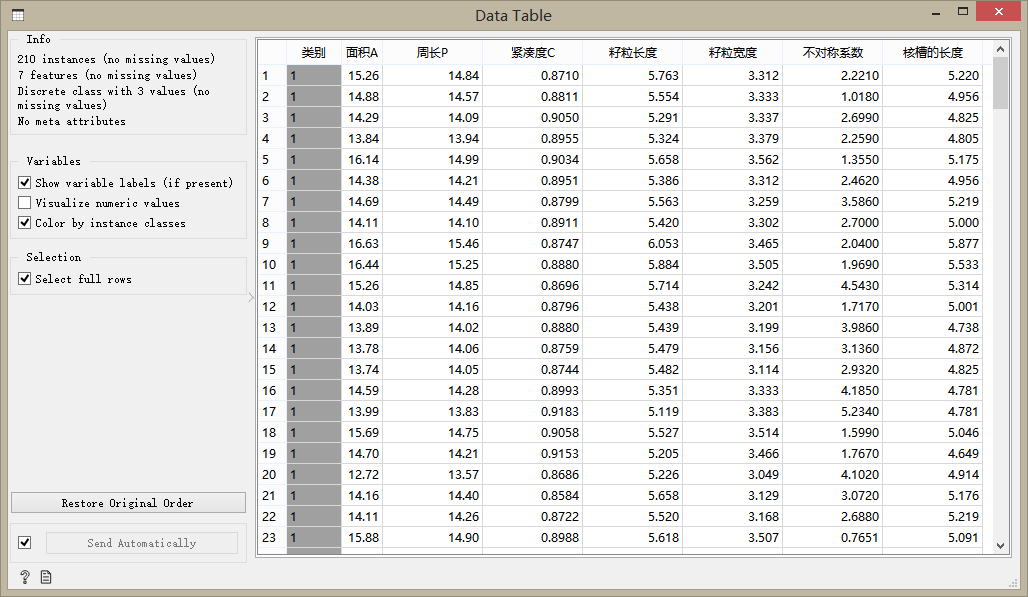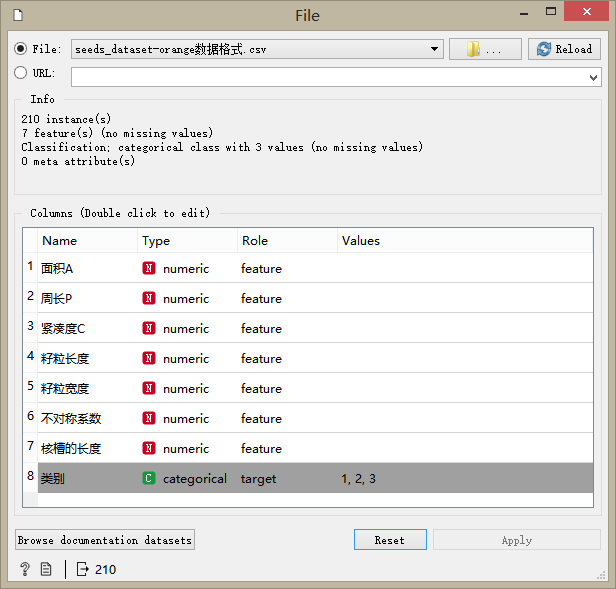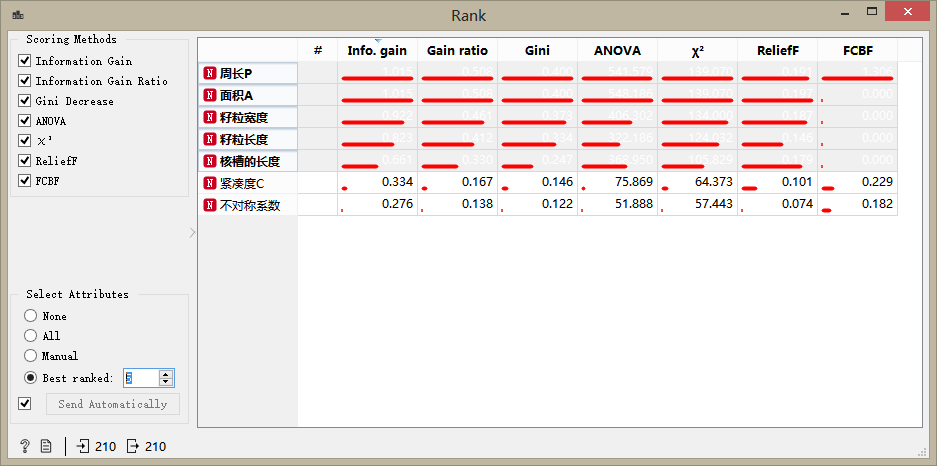 使用Data Table組件查看數據，顯示的一部分數據  ### 數據預處理 打開orange軟件，進行數據預處理  加入文件（File）組件，設置數據源（File）為前面下載并處理后的數據集，設置類別的角色（Role）為目標（target），并將其類型（Type）改成目錄化（Categorical）  特征排序組件（Rank）可以根據數據特征的相關性對其進行排名和篩選，我們只關心那些對分類有較大幫助的特征（信息量比較大的），雙擊控件：  可以看出，緊湊度（compactness）和不對稱性（asymmetry）特征的信息量值很低，故將其篩除。 > 可以用數據分布組件（Distributions）通過觀察緊湊度（compactness）和不對稱性（asymmetry）特征值的分布進行驗證。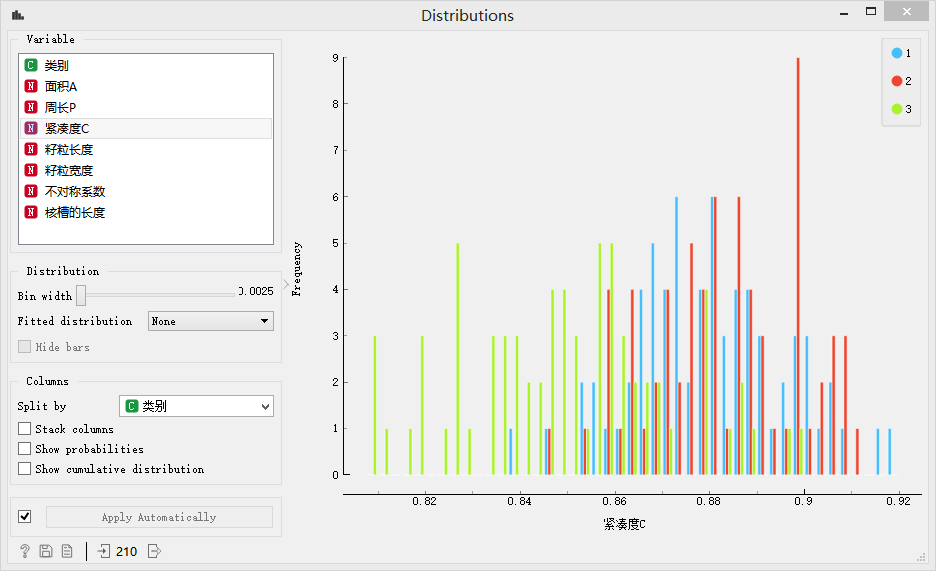 緊湊度的統計分布  > 分布圖中可以看出3種類別的數據都混合在一起，因此該特征很難區分不同的類別的種子，因此不合適作為分類的特征，或者說該特征對分類任務來說提供的信息量是很少的。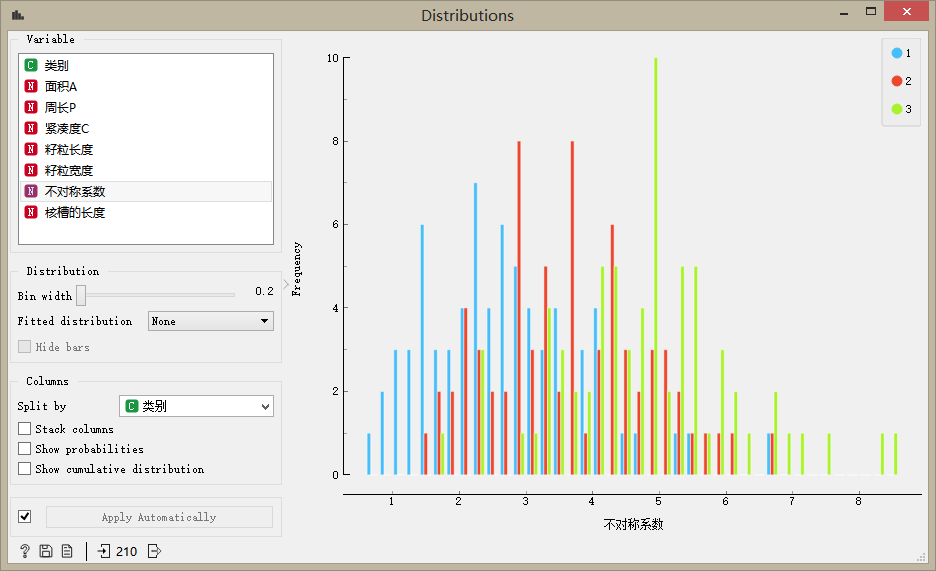 不對稱系統的統計分布  ## 聚類 ### K-means算法 k均值聚類算法（k-means clustering algorithm）是一種迭代求解的算法，其步驟是： 預將數據分為K組，則隨機選取K個對象作為初始的聚類中心，然后計算每個對象與各個種子聚類中心之間的距離，把每個對象分配給距離它最近的聚類中心。聚類中心以及分配給它們的對象就代表一個聚類。每分配一個樣本，聚類的聚類中心會根據聚類中現有的對象被重新計算。這個過程將不斷重復直到滿足某個終止條件。終止條件可以是沒有（或最小數目）對象被重新分配給不同的聚類，沒有（或最小數目）聚類中心再發生變化，誤差平方和局部最小。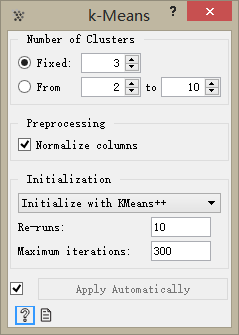 雙擊K-means控件，設置算法參數： > 輸入固定簇數（Number of Clusters）：3  > 選擇使用K-means++算法進行初始化 ### 層次聚類 先用距離組件（Distances）計算成對距離的矩陣，然后用層次聚類組件（Hierarchical Clustering）顯示從輸入距離矩陣構造的層次聚類的樹形圖 ?????? 選擇Top N = 3,傳入數據流到Scatter Plot控件進行可視化： 結果分析： ?????? 用Silhouette Plot輪廓組件評價聚類效果。數據越靠近數據簇中心，輪廓值越大；離簇中心越遠，輪廓值越小：0為位于兩簇之間的點，負數為錯誤劃分到別的簇中。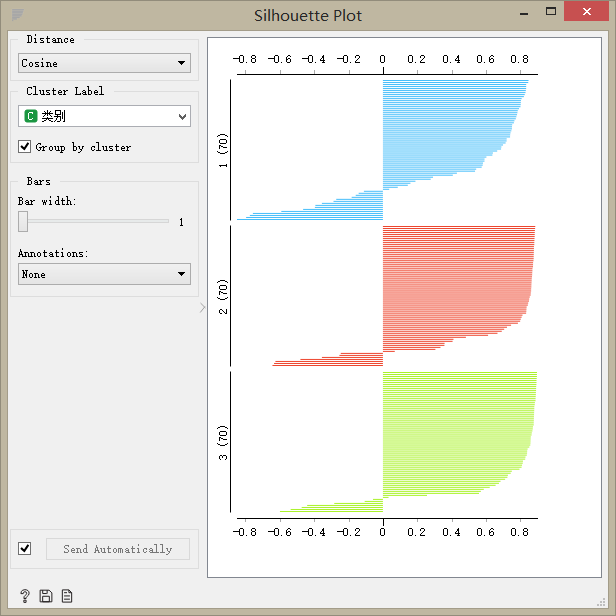 K-means輪廓圖：  K-means++輪廓圖 層次輪廓圖： ?????? 通過對比其輪廓圖，我們發現：在對該數據進行聚類時，K-means算法要比層次聚類要好，層次聚類中有出現負值；而k-means++算法將數據聚成兩簇，沒有達到我預期得到的聚類結果。