[TOC] # 應用決策樹幫助老師實施差異化教學 # 學習目標 1. 什么是監督式學習與無監督學習？ 2. 聚類算法的作用？ 3. 如何通過『數據集』組件下載數據。 4. 歐幾里德距離計算。 5. 層次聚類算法模型基本邏輯。 6. 如何使用『箱線圖』觀察數據分布。 # 任務描述 假設你是一個班主任，拿到學生的入學成績，剛接觸學生，對學生不是很了解，那么我們如何對學生有效的分組幫助他們快速的成長，怎么分組開展個性化教學呢？ 傳統簡單的辦法，我們習慣根據考試成績來分組，但是每個學生不同學科的成績差異很大，數學好的英語可能很差，我們常說物理類聚，人以群分，有相同學習目標的人放在一起容易形成共鳴，學習積極性也會高很多，因此我們希望能夠幫助老師把學生合理的分組，這個問題事先我們并不知道學生屬于哪個組，也不知道具體需要分成幾個組，不大適合使用K均值來實現，我們應用決策樹幫助老師實施差異化教學分組。 # 實驗數據 便于說明算法的工作原理，我們采集了12個人兩門課程的入學成績數據。 在工作面板上拖動一個數據表組件（Data Table）連接文件組件（File）可以查看數據表格。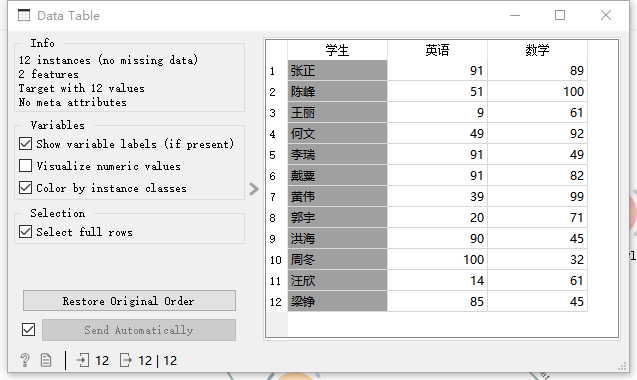  # 層次聚類 層次聚類試圖在不同層次對數據集進行劃分，從而形成樹形的聚類結構。數據集劃分可采用"自底向上"的聚合策略，也可采用"自頂向下"的分拆策略。 如圖所示， 我們將全部12個同學的成績用散點圖繪制，根據常識，我們將樣本距離近的歸為一類，直觀的，我們將這12個樣本分為4類比較合理，分別表示英語和數學成績都正常發展的，英語偏科的，數學偏科的以及英語和數學發展都相對落后的。圖中用四個不同顏色的區域表示這個類同學。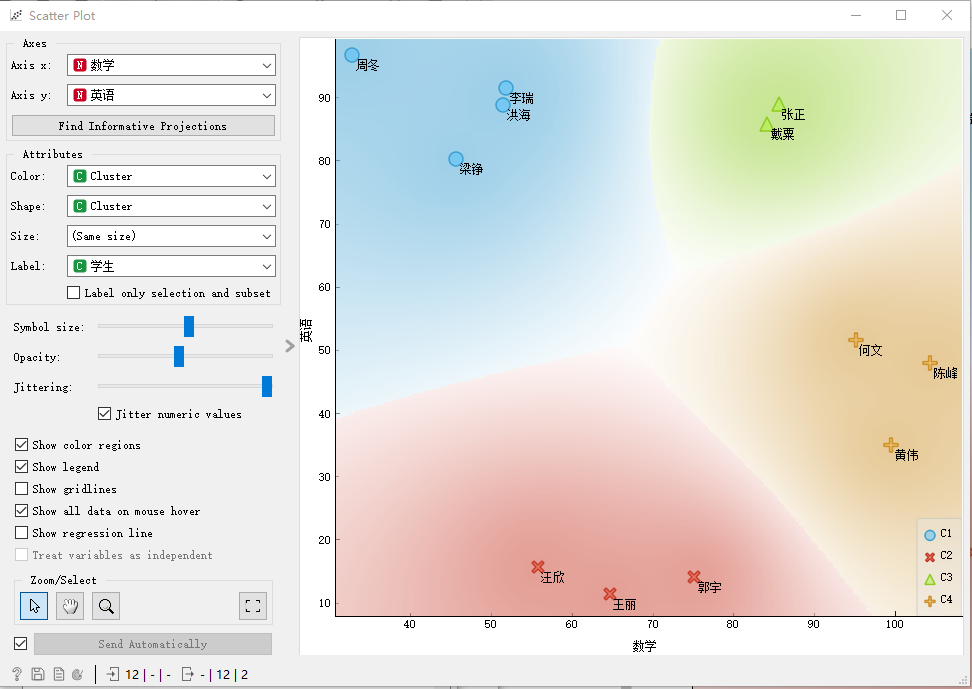  為達到分類的目的，首先應用距離組件（Distances）計算樣本對之間的距離，為了簡單期間，我們選擇歐式距離，也就是平時我們說的平面上兩個點之間的直線距離。 那么層次 聚類怎么工作的呢？首先我們把每一個點看成是一個類，從散點圖上我們可以看出李瑞洪海和之間的距離最近，因此我們首先把這兩個點（類）歸為一類，并用這兩個點的中心來代表這個類，重復這個過程，每次合并兩個類，直到整個集合都被歸為一個類，層次聚類的過程如圖所示，最后。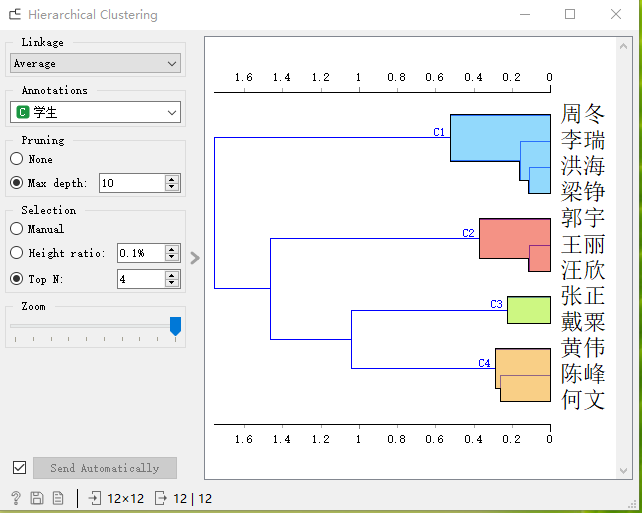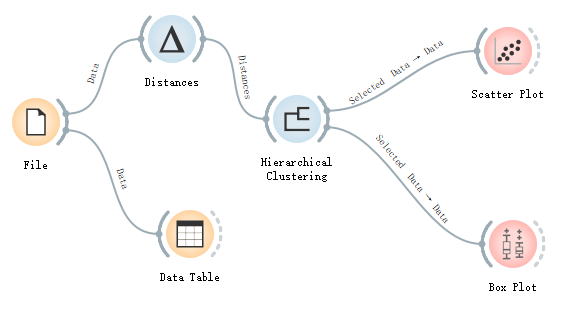 我們反向操作，選擇一個合適的層數來決定具體我們要劃分為多少個類  # 實驗設計  # 實驗分析 最后我們借助箱線圖來分析分類的結果。 ## 箱線圖 > 箱形圖（Box-plot）又稱為盒須圖、盒式圖或箱線圖，是一種用作顯示一組數據分散情況資料的統計圖。因形狀如箱子而得名。在各種領域也經常被使用，它主要用于反映原始數據分布的特征，還可以進行多組數據分布特征的比 較。箱線圖的繪制方法是：先找出一組數據的上邊緣、下邊緣、中位數和兩個四分位數；然后， 連接兩個四分位數畫出箱體；再將上邊緣和下邊緣與箱體相連接，中位數在箱體中間。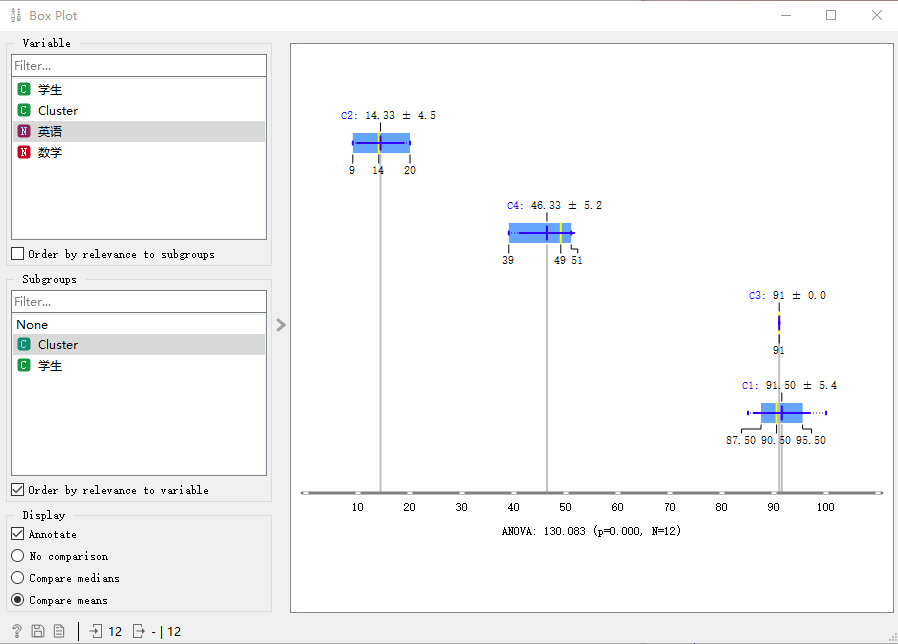  不同于分類問題，聚類樣本沒有沒有已知的標簽，類似于學生的分組，沒有一個具體的標準去評判分組的好壞，要根據具體的應用的情況。