[toc]
# 時間復雜度
一段代碼運行的時間。
## 分析代碼執行的次數
通過分析 `代碼執行的條數` 來衡量時間復雜度。
比如:
~~~
function hello() {
console.log('hello')
}
~~~
這個函數執行了 1 代碼。 漸進復雜度:O(1)
再比如:
~~~
function hello1() {
console.log('hello');
console.log('hello');
console.log('hello')
}
~~~
這個函數執行的代碼次數是 3。 O(1)
再比如:
~~~
function hello2() {
for(let i=0;i<20;i++) {
console.log('hello')
}
}
~~~
這段代碼我們就說,這段代碼執行了20次語句。
~~~
function hello3() {
for(let i=0;i<20;i++) {
console.log('hello')
console.log('hello')
console.log('hello')
}
}
~~~
這段代碼花費的時間是:60 O(1)
~~~
function hello4(n) {
for(let i=0;i<n;i++) {
console.log('hello')
console.log('hello')
console.log('hello')
}
}
~~~
這段代碼花費的時間是:3n O(n)
~~~
function hello5(n) {
for(let i=0;i<n;i++) {
console.log('hello') // 被執行 n 次
console.log('hello') // 被執行 n 次
for(let j=0;j<n;j++) {
console.log('hello') // 被執行 n * n 次(n的平方)
console.log('hello') // 被執行 n * n 次(n的平方)
}
}
}
~~~
這段代碼花費的時間是:n + n + n^2 + n^2 = 2n + 2n^2 = 2(n^2+n) O(n^2)
總結:代碼花費的時間主要就是通過代碼被執行的次數來判斷,有一些復雜的代碼是需要很強的數學功底才能算出執行的次數,對于此我們知道常見的即可。
練習:以下代碼執行次數是多少?
~~~
function hello6(n) {
for(let i=0;i<n;i++) {
if(n%2==0) {
console.log('hello') // n/2
}
console.log('hello') // n
for(let j=0;j<n;j++) {
console.log('hello') // n^2
}
}
}
~~~
代碼執行的次數:n^2 + 1.5n O(n^2)
~~~
function hello7(n) {
for(let i=n;i>=0;i=i/2) {
console.log('hello') // log2N(開對數,log 以2為底的n)
}
}
~~~
代碼執行的次數:logn(默認以2為底) O(logn)
## 漸進時間復雜度
實際工作中,代碼執行次數計算的再精確意義也不大,比如:兩代碼。
代碼 a 的執行次數:100n。
代碼 b 的執行次數:n^2。
這時兩段如何判斷誰的性能更好?
當 n 小時,代碼b快,當n值大時,代碼a快。
所以,我們一般采用 `漸進的時間復雜度` 來衡量:當 n 無限增大時,代碼執行次數增長的趨勢。
所以我們平時說的時間復雜度,其實是指:`漸進時間復雜度`。
在計算漸進時間復雜度時有以下幾個原則:
1. 變量前面的系統數,一般直接忽略,比如:10n --> n
2. 如果有最高階,只保留最階,比如:n^5 + n^2 ---> n^5
3. 如果代碼執行的次數穩定不變,那么就用 1 來表示,比如: 5 --> 1
使用 大O 表示法的符號來表示漸進復雜度。
比如:以下代碼執行次數是 2(n^2+n),那么它的漸進時間復雜度用大O表示法來表示:
~~~
function hello5(n) {
for(let i=0;i<n;i++) {
console.log('hello') // 被執行 n 次
console.log('hello') // 被執行 n 次
for(let j=0;j<n;j++) {
console.log('hello') // 被執行 n * n 次(n的平方)
console.log('hello') // 被執行 n * n 次(n的平方)
}
}
}
~~~
漸進時間復雜度為:O(n^2)
總結:
1. 使用大O表示法來表示一段代碼的時間復雜度
2. 大O代表的是`漸進時間復雜度`:當n無限增大,代碼花費時間的增長趨勢。
分析一段代碼的時間復雜度的流程:
1. 先分析代碼執行的次數,得到一個公式
2. 根據規則轉成 大O 表示法
## 常見的幾種時間復雜度
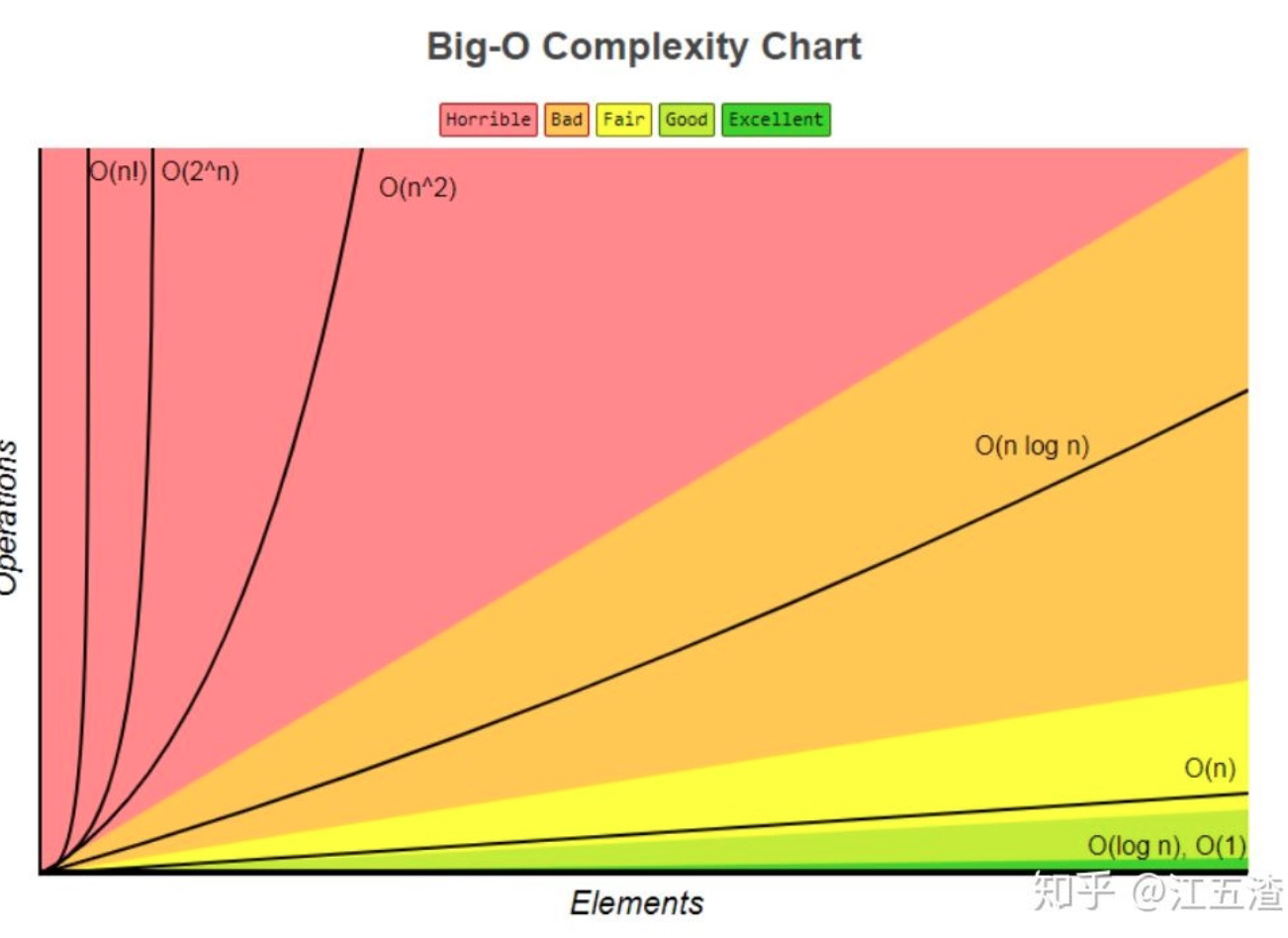
# 最好、平均、最壞時間復雜度
一段代碼的時間復雜度還和要操作的數據相關,比如:如果要排序一個數組,然后這個數組是已經排序好的數組,那么對這個數組進行排序,速度會非常快。這屬于最好情況。
所以我們一般說時間復雜度時,一般都是是指:“最壞時間復雜度”。
