# 介紹
1. AVL 樹是最早被發明的自平衡二叉樹
2. AVL 樹得名于它的發明者G. M. Adelson-Velsky和E. M. Landis,他們在1962年的論文中發表了它。
# 構建 AVL 樹
為了保證一樹是時刻保持平衡,我們需要在向節點中插入、刪除新節點時通過 `旋轉` 來調整樹的結構。
如何實現二叉樹調整平衡,要通過二叉樹的 `旋轉` 來實現。
二叉樹可以分為四種情況,不同的情況進行不同的旋轉:
L:left 左
LL: 左左型
R:right 右
RR:右右型
LR:左右型
RL:右左型
* LL型二叉樹 :右旋轉
* RR型二叉樹:左旋轉
* LR型二叉樹:先左旋轉再右旋轉
* RL型二叉樹:先右旋轉再左旋轉
## LL 型
對于節點傾向于左邊的情況,我們稱之為 `LL型`。
這個時候我們需要進行 `右旋轉` 操作,使它恢復平衡:
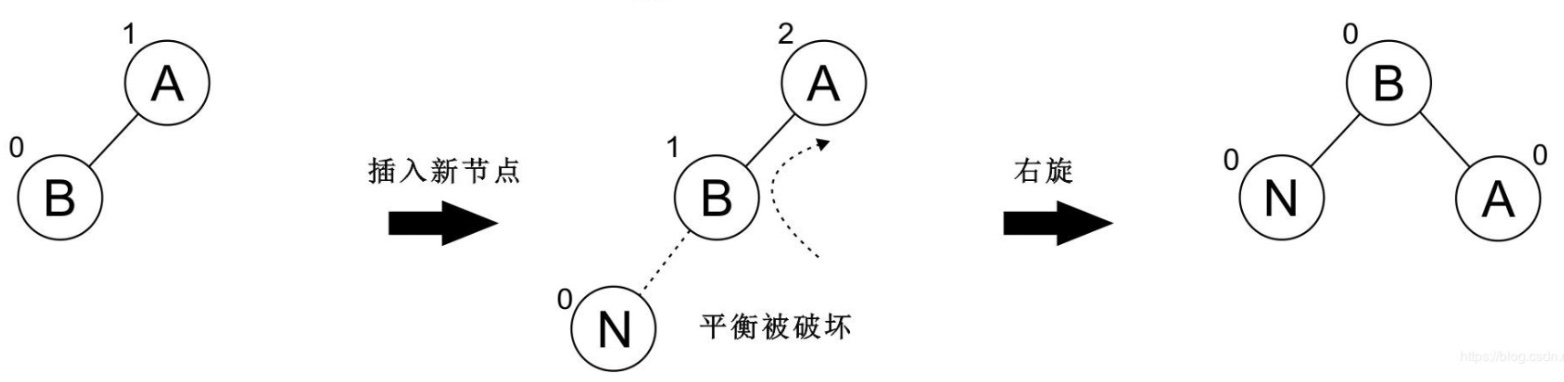
再看一個例子:
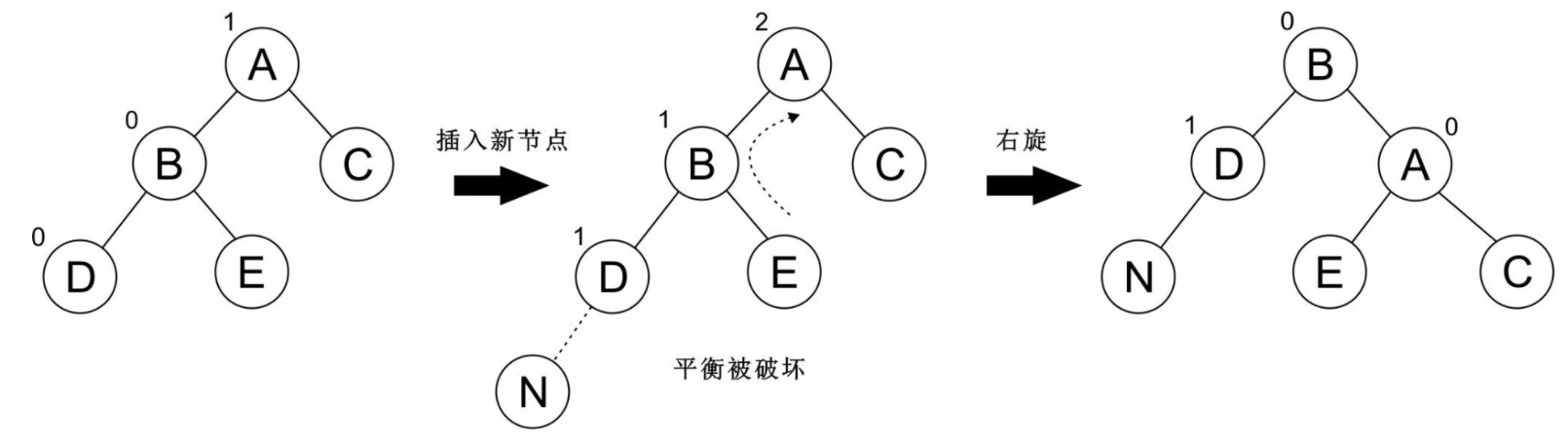
再看一個例子:

## RR 型
對于節點傾向于右邊的情況,我們稱之為 `RR型`。
這個時候我們需要進行 `左旋轉` 操作,使它恢復平衡:
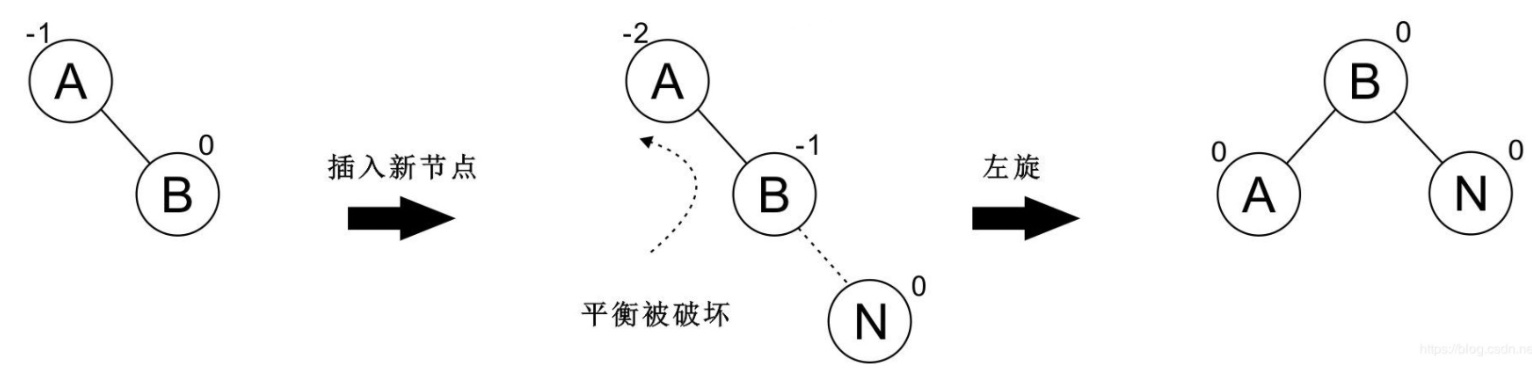
再看一個例子:
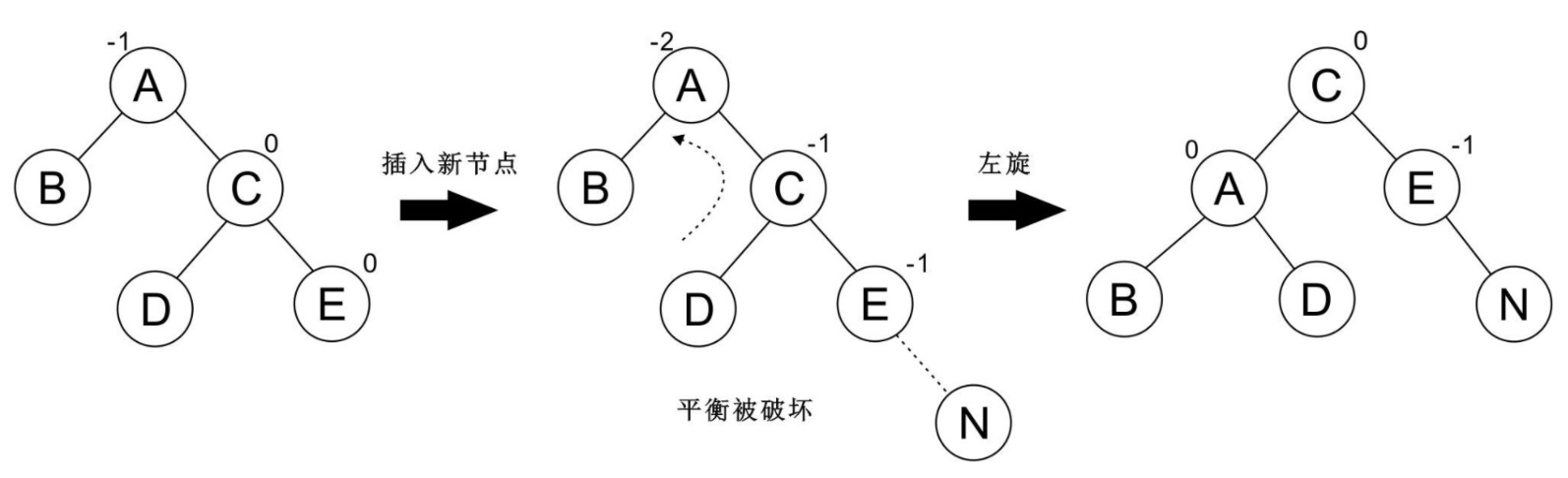
再看一個例子:

## LR 型
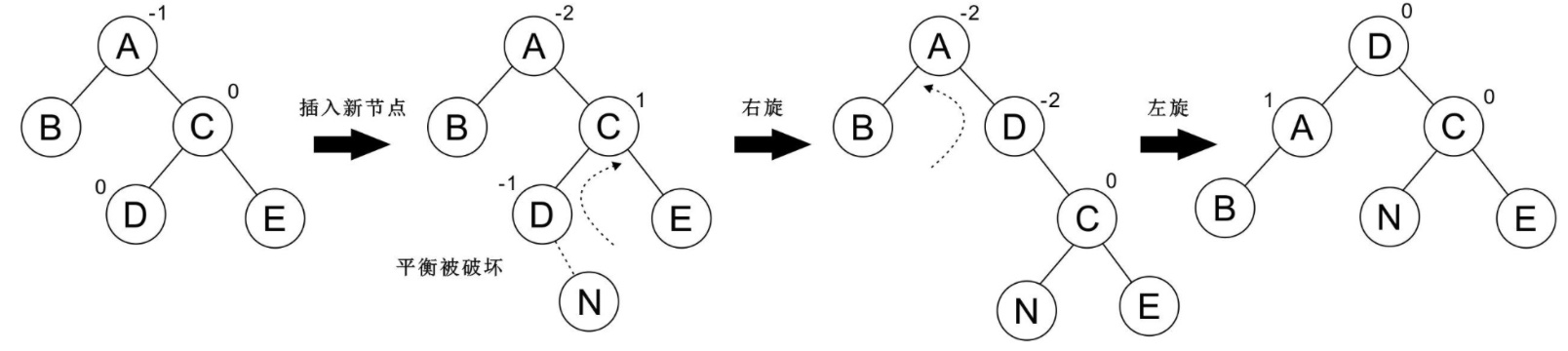
以下樹為 LR 型,這種情況需要旋轉兩次:先左旋轉再右旋轉:
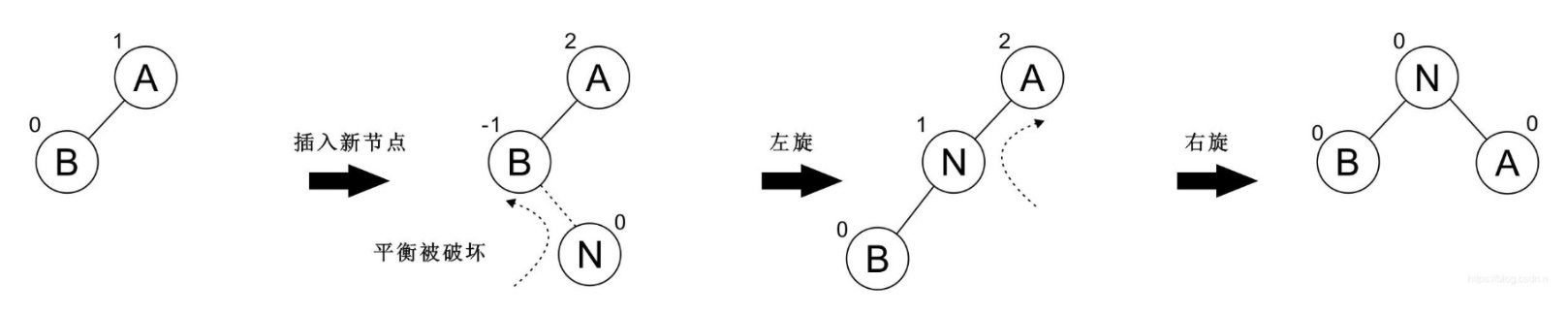
再看一個例子:
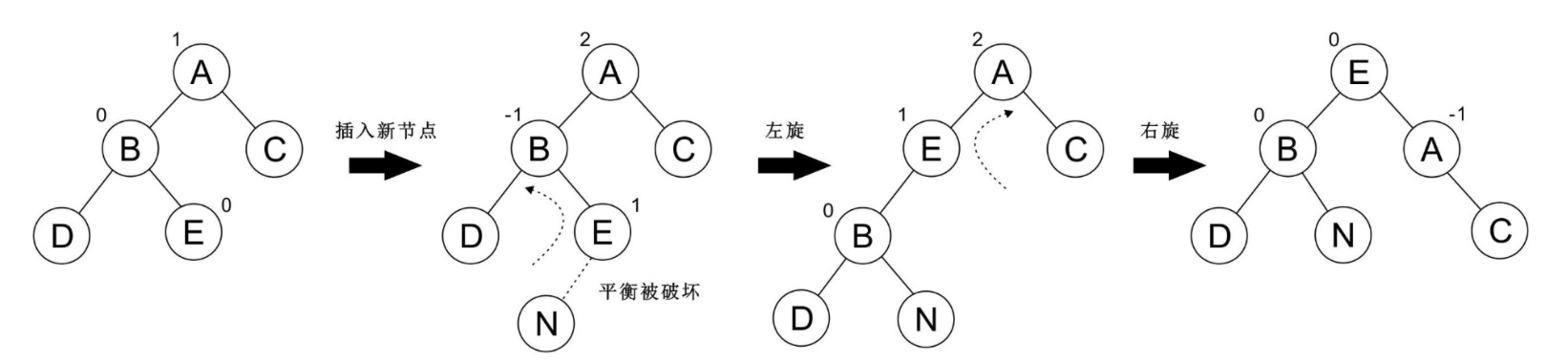
再看一個例子:
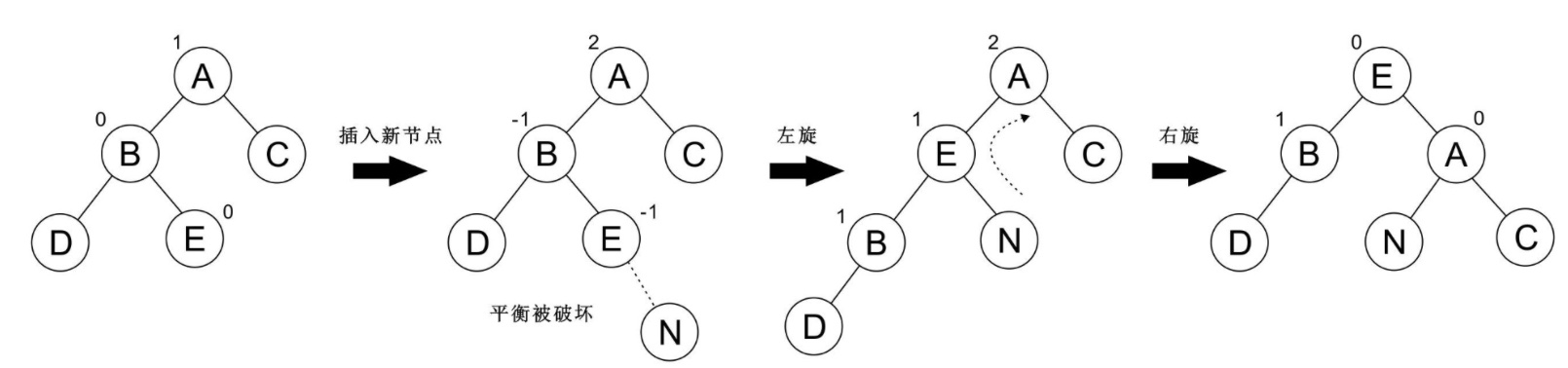
## RL 型
看一個例子:

再看一個例子:
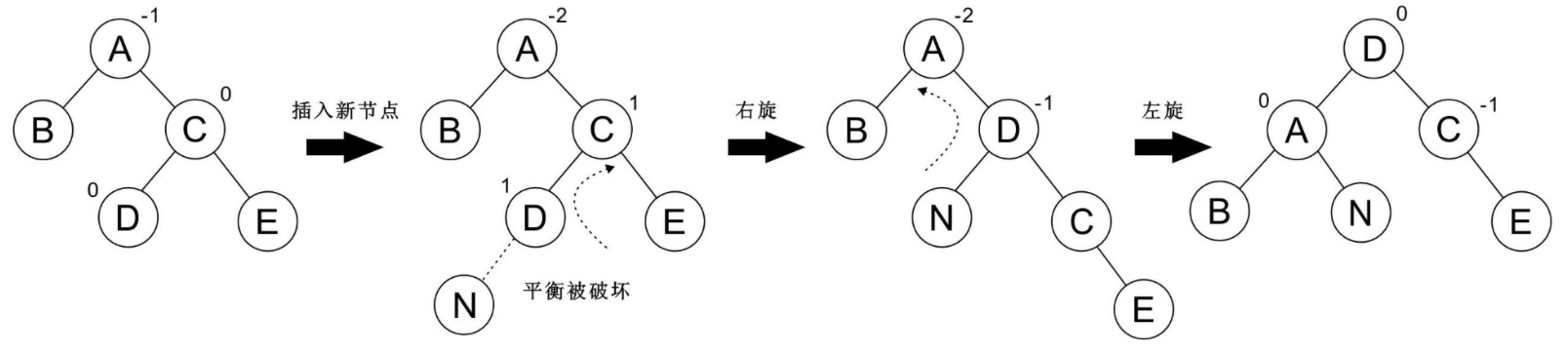
再看一個例子:
# 代碼實現
## 平衡因子
總結:
1. 平衡因子:左子樹的高度-右子樹的高度
2. 如果平衡因子大于等于 2 說明這個節點不平衡
3. 如果平衡因子是正數,說明:L 型(左高)
4. 如果平衡因子是負數,說明:R 型(右高)
## 獲取一個的高度
節點高度:左右節點中到葉子節點最多的邊數。
~~~
// 獲取節點高度
getHeight(node) {
if(node === null) return 0
// 左右節點中最長的邊數
return Math.max(this.getHeight(node.left), this.getHeight(node.right)) + 1
}
~~~
## 添加四種旋轉方法
### 左旋
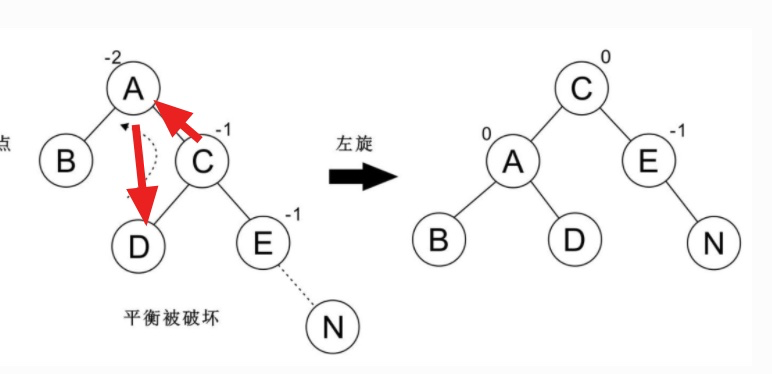
代碼:

### 右旋
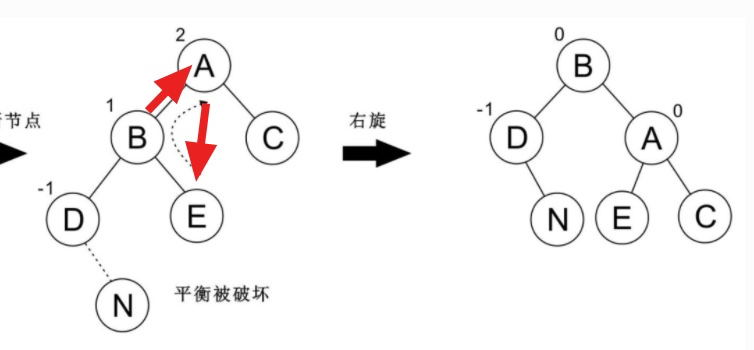
代碼:

### 先左后右
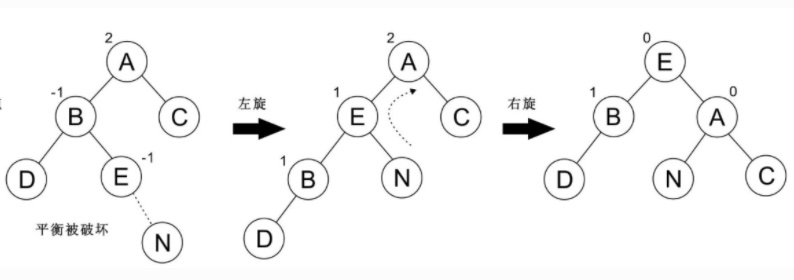
代碼:

### 先右后左
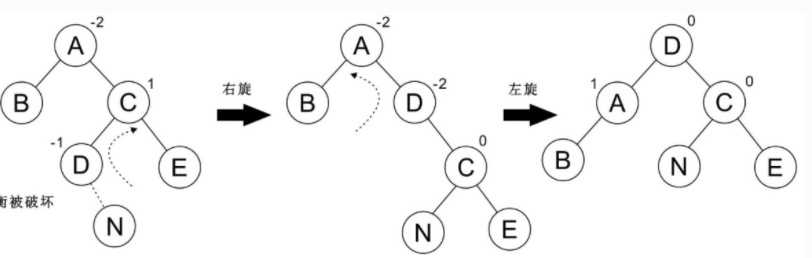
代碼:

### 調整二叉樹
計算一個節點的高度并判斷是否平衡,如果不平衡,就判斷是什么型并進行相應的旋轉以保持平衡:
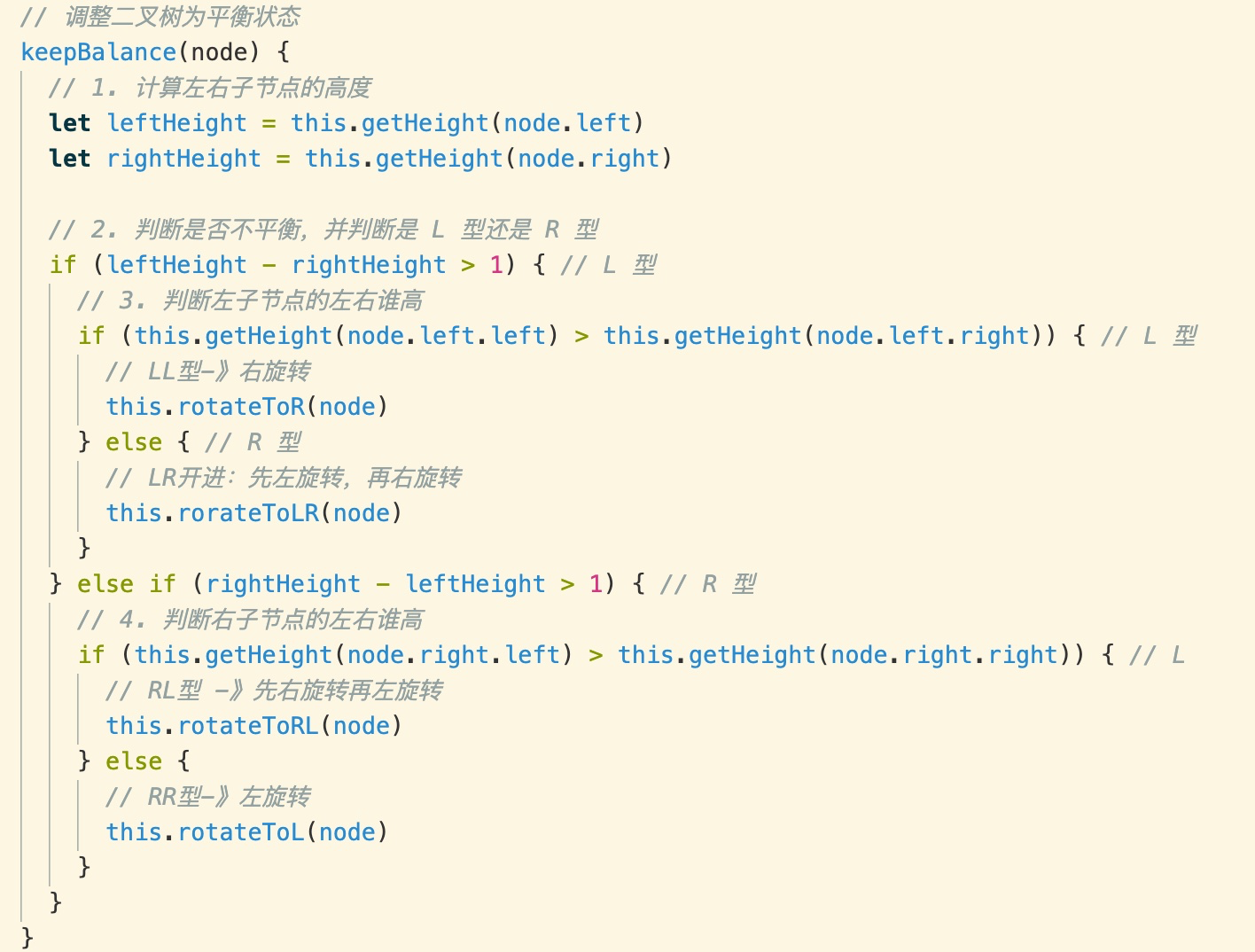
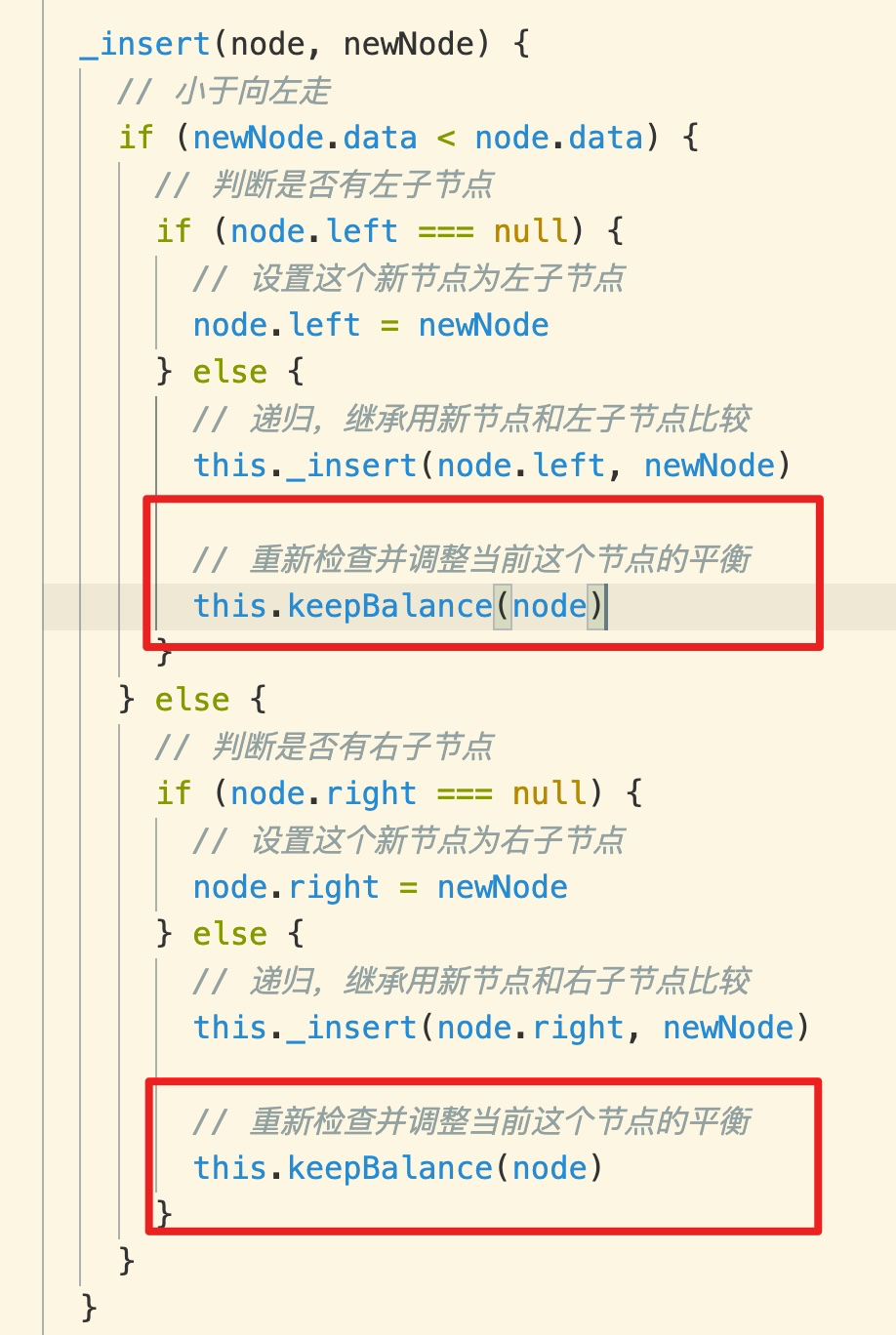
### 在添加節點時檢查并調整節點
在每次添加一個新節點時,都有可能打破平衡,需要檢查并調整:
修改添加節點的代碼,在向兒子節點中添加節點時要重新檢查并調整
# 完整 AVL Tree 代碼
~~~
// 定義節點類
class Node {
constructor(data) {
this.data = data // 數據
this.left = null // 左子節點
this.right = null // 右子節點
}
}
// AVL樹(自平衡二叉搜索樹)
class AVLTree {
constructor() {
this.root = null // 根節點
this.length = 0 // 樹中節點的數量
}
// 向樹中插入一條記錄
insert(data) {
// 1. 創建新的節點
let newNode = new Node(data)
// 2.放到樹中
// 如果是空樹
if (this.root === null) {
// 設置這個新節點為樹根
this.root = newNode
} else {
// 從根節點開始比較
this.root = this._insert(this.root, newNode)
}
}
_insert(node, newNode) {
if (node === null) {
node = newNode
return node
}
// 小于向左走
if (newNode.data < node.data) {
// 判斷是否有左子節點
if (node.left === null) {
// 設置這個新節點為左子節點
node.left = newNode
} else {
// 遞歸,繼承用新節點和左子節點比較
node.left = this._insert(node.left, newNode)
// 重新檢查并調整當前這個節點的平衡
node = this.keepBalance(node)
}
} else {
// 判斷是否有右子節點
if (node.right === null) {
// 設置這個新節點為右子節點
node.right = newNode
} else {
// 遞歸,繼承用新節點和右子節點比較
node.right = this._insert(node.right, newNode)
// 重新檢查并調整當前這個節點的平衡
node = this.keepBalance(node)
}
}
return node
}
// 判斷樹中是否包含某一個數
has(data) {
// 從根節點開始查找
return this._has(this.root, data)
}
_has(node, data) {
// 如果節點為空,說明樹中沒有這個數
if (node == null) {
return false
}
// 如果值和前節點值相同,找到了
if (data == node.data) {
return true
} else if (data < node.data) {
// 到左子樹中查找
return this._has(node.left, data)
} else if (data > node.data) {
// 到右子樹中查找
return this._has(node.right, data)
}
}
// 前序遍歷(根左右)
preOrder() {
this._preOrder(this.root)
}
// 開始的節點
_preOrder(node) {
if (node === null) return
// 根
console.log(node.data)
// 左
this._preOrder(node.left)
// 右
this._preOrder(node.right)
}
// 中序遍歷(左根右)
midOrder() {
this._midOrder(this.root)
}
// 開始的節點
_midOrder(node) {
if (node === null) return
// 左
this._midOrder(node.left)
// 根
console.log(node.data)
// 右
this._midOrder(node.right)
}
// 后序遍歷(左右根)
postOrder() {
this._postOrder(this.root)
}
// 開始的節點
_postOrder(node) {
if (node === null) return
// 左
this._postOrder(node.left)
// 右
this._postOrder(node.right)
// 根
console.log(node.data)
}
// 層序遍歷
layerOrder() {
// 1. 創建一個隊列(先入先出)
let queue = []
// 2. 先根節點放到隊尾
queue.push(this.root)
// 3. 循環隊列
let node
while (queue.length > 0) {
// 4. 從隊頭取出節點
node = queue.shift()
// 5. 左右子節點放入隊尾
if (node.left !== null) queue.push(node.left)
if (node.right !== null) queue.push(node.right)
// 6. 輸出當前節點(使用這個節點)
console.log(node.data)
}
}
// 獲取節點高度
getHeight(node) {
if (node === null) return 0
// 左右節點中最長的邊數
return Math.max(this.getHeight(node.left), this.getHeight(node.right)) + 1
}
// 左旋轉
rotateToL(node) {
// 1. 取出右子節點(C)
let tmp = node.right
// 2. 父節點指向右子節點的左子節點
node.right = tmp.left
// 3. 右子節點的左子節點指向父節點
tmp.left = node
// 4. 返回新的頂點
return tmp
}
// 右旋轉
rotateToR(node) {
let tmp = node.left
node.left = tmp.right
tmp.right = node
return tmp
}
// 先左旋再右旋轉
rorateToLR(node) {
// 讓左子節點左旋轉,并讓旋轉之后的頂點做為左子節點
node.left = this.rotateToL(node.left)
// 再讓當前節點右旋轉
return this.rotateToR(node)
}
// 先右旋轉再左旋轉
rotateToRL(node) {
// 讓右子節點先右旋轉,并用新的頂點做為右子節點
node.right = this.rotateToR(node.right)
// 當前節點左旋
return this.rotateToL(node)
}
// 調整二叉樹為平衡狀態
keepBalance(node) {
if(node === null) return node
// 1. 計算左右子節點的高度
let leftHeight = this.getHeight(node.left)
let rightHeight = this.getHeight(node.right)
// 2. 判斷是否不平衡,并判斷是 L 型還是 R 型
if (leftHeight - rightHeight > 1) { // L 型
// 3. 判斷左子節點的左右誰高
if (this.getHeight(node.left.left) >= this.getHeight(node.left.right)) { // L 型
// LL型-》右旋轉
node = this.rotateToR(node)
} else { // R 型
// LR開進:先左旋轉,再右旋轉
node = this.rorateToLR(node)
}
} else if (rightHeight - leftHeight > 1) { // R 型
// 4. 判斷右子節點的左右誰高
if (this.getHeight(node.right.left) >= this.getHeight(node.right.right)) { // L
// RL型 -》先右旋轉再左旋轉
node = this.rotateToRL(node)
} else {
// RR型-》左旋轉
node = this.rotateToL(node)
}
}
return node
}
// 刪除數據
deleteNode(data) {
// 從根開始比較刪除
this.root = this._deleteNode(this.root, data)
}
_deleteNode(node, data) {
// 沒有子節點了,不用刪除
if (node == null) return null
if (data < node.data) {
// 往左走
node.left = this._deleteNode(node.left, data)
// 重新調整節點的平衡
return this.keepBalance(node)
} else if (data > node.data) {
// 往右走
node.right = this._deleteNode(node.right, data)
// 重新調整節點 平衡
return this.keepBalance(node)
} else {
// 如果相等就是找到了節點位置 ,要刪除當前節點
// 情況一、有兩個子節點
if (node.left !== null && node.right !== null) {
// 取出右子節點
let tmp = node.right
// 找出最小的節點(最左邊的分支)
while (tmp.left !== null) {
tmp = tmp.left
}
// 把最小的值賦給當前節點
node.data = tmp.data
// 從右分支中刪除這個最小的節點
node.right = this._deleteNode(this.right, tmp.data)
// 重新調整平衡
node = this.keepBalance(node)
return node
} else {
// 情況二、沒有子節點
if (node.left === null && node.right === null) {
node = null
return null
}
// 情況三、只有左節點
if (node.left !== null) {
// 左節點替換當前節點
node = node.left
return node
}
// 情況四、只有右節點
if (node.right !== null) {
// 右節點替換當前節點
node = node.right
return node
}
}
}
}
}
const avl = new AVLTree()
avl.insert(3)
avl.insert(2)
avl.insert(1)
avl.insert(4)
avl.insert(5)
avl.deleteNode(1)
console.log(avl.root)
~~~
