# 拓撲排序
在圖論中,拓撲排序(Topological Sorting)是一個有向無環圖(DAG, Directed Acyclic Graph)的所有 `頂點的線性序列`。
且該序列必須滿足下面兩個條件:
1. 每個頂點出現且只出現一次。
2. 若存在一條從頂點 A 到頂點 B 的路徑,那么在序列中頂點 A 出現在頂點 B 的前面。
## 有向無環圖
無環:由任意一點出點,無法回到這個點。
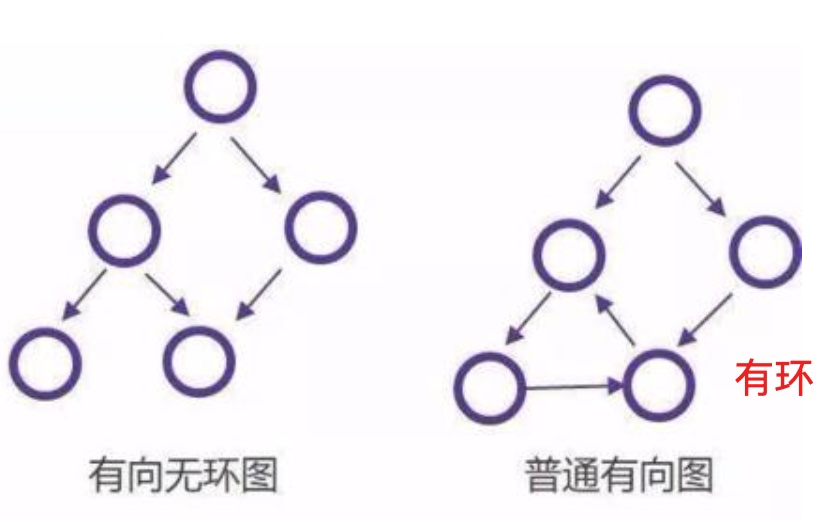
## 拓撲排序用途
拓撲排序通常用來把圖 “排序” 成具有依賴關系的一個線性序列。
## 實現思路
實現流程:
1. 從 DAG 圖中選擇一個沒有前驅(即入度為0)的頂點并輸出。
2. 從圖中刪除該頂點和所有以它為起點的有向邊。
3. 重復 1 和 2 直到當前的 DAG 圖為空或當前圖中不存在無前驅的頂點為止。后一種情況說明有向圖中必然存在環。
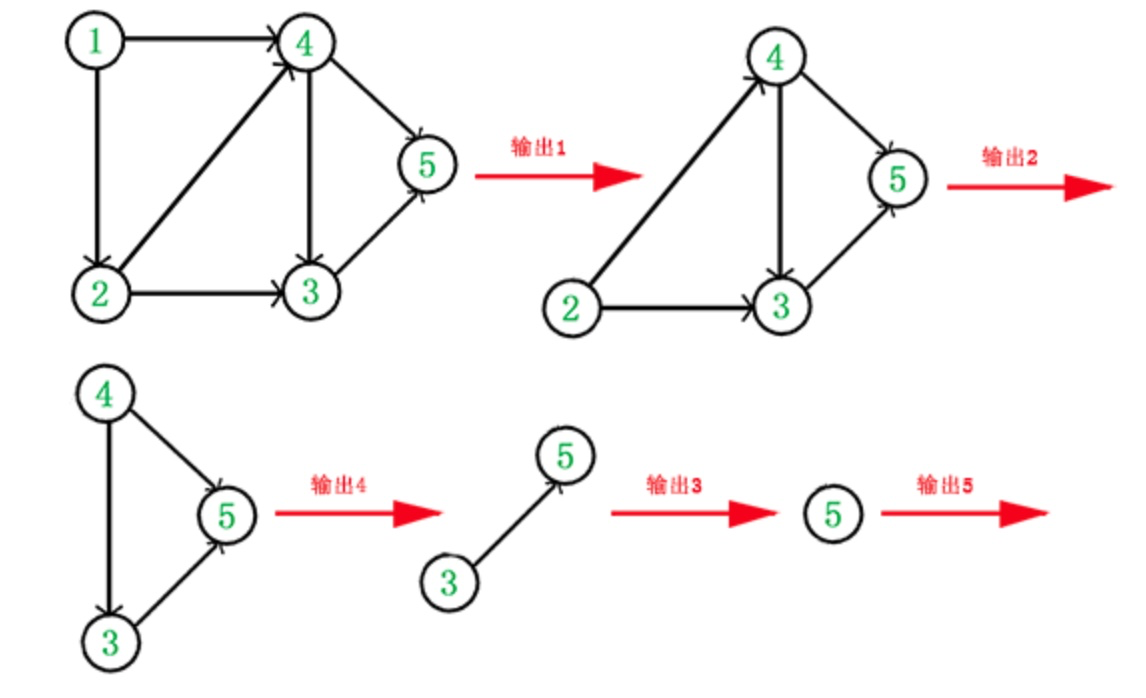
所以輸出序列為:1,2,4,3,5
