[toc]
# 介紹
堆(Heap)是一種特殊的二叉樹:
1. 堆是一個完全二叉樹
2. 堆中每一個節點的值都必須大于等于(或小于等于)其子樹中的每個節點的值
# 分類
堆分為兩種:`大頂堆` 和 `小頂堆` 。
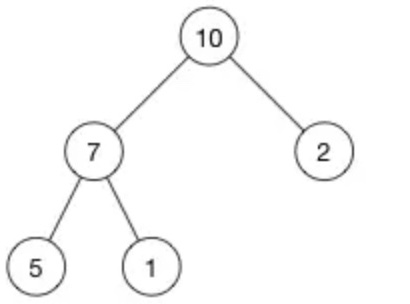
* 大頂堆:父頂點的值大于所有子頂點的值。
* 小頂堆:父頂點的值小于所有子頂點的值。
大頂堆:
小頂堆:
# 存儲
堆是一種二叉樹,有兩種存儲方式:
- 數組
- 鏈表
堆是一種完全二叉樹,而完全二叉樹使用 `數組` 存儲比較合適。
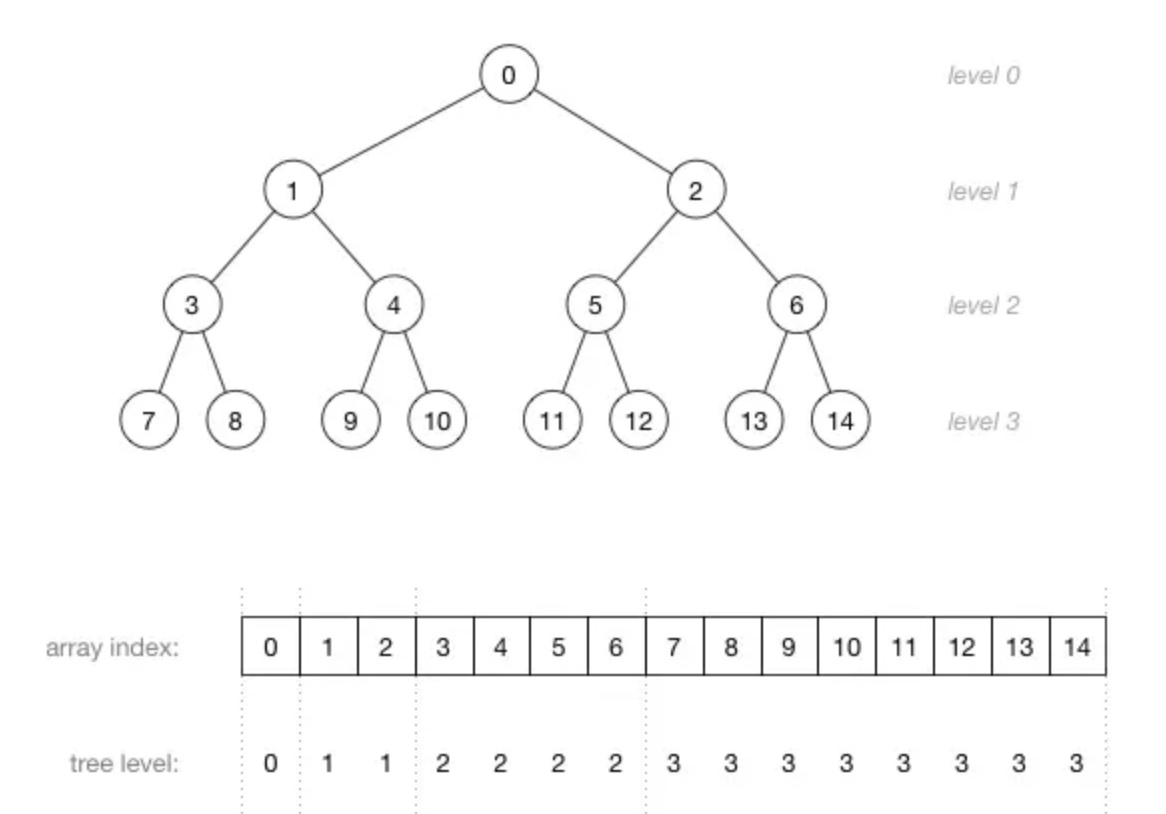
當以數組保存二叉樹時有以下幾個重要公式。
1. 對于下標為 i 節點(子節點)
左子節點下標:2i+1
右子節點下標:2i+2
2. 對于下標為 i 的節點(父節點)
父節點下標:Math.floor( (i-1) / 2 )
3. 最后一個非葉子節點的節點的下標
Math.floor(len/2) - 1
# 應用場景
1. 排序 ---》 堆排序(時間復雜度:O(nlogn)
2. 優先隊列(優先級高的放到前面)
# 操作
二叉堆的操作有三種:
- 插入節點
- 刪除節點
- 構建二叉堆
## 插入節點
當向二叉堆中插入新節點時的操作:
1. 將新節點先放到 `最后`
2. 然后依次和父節點比較,然后 `上浮`
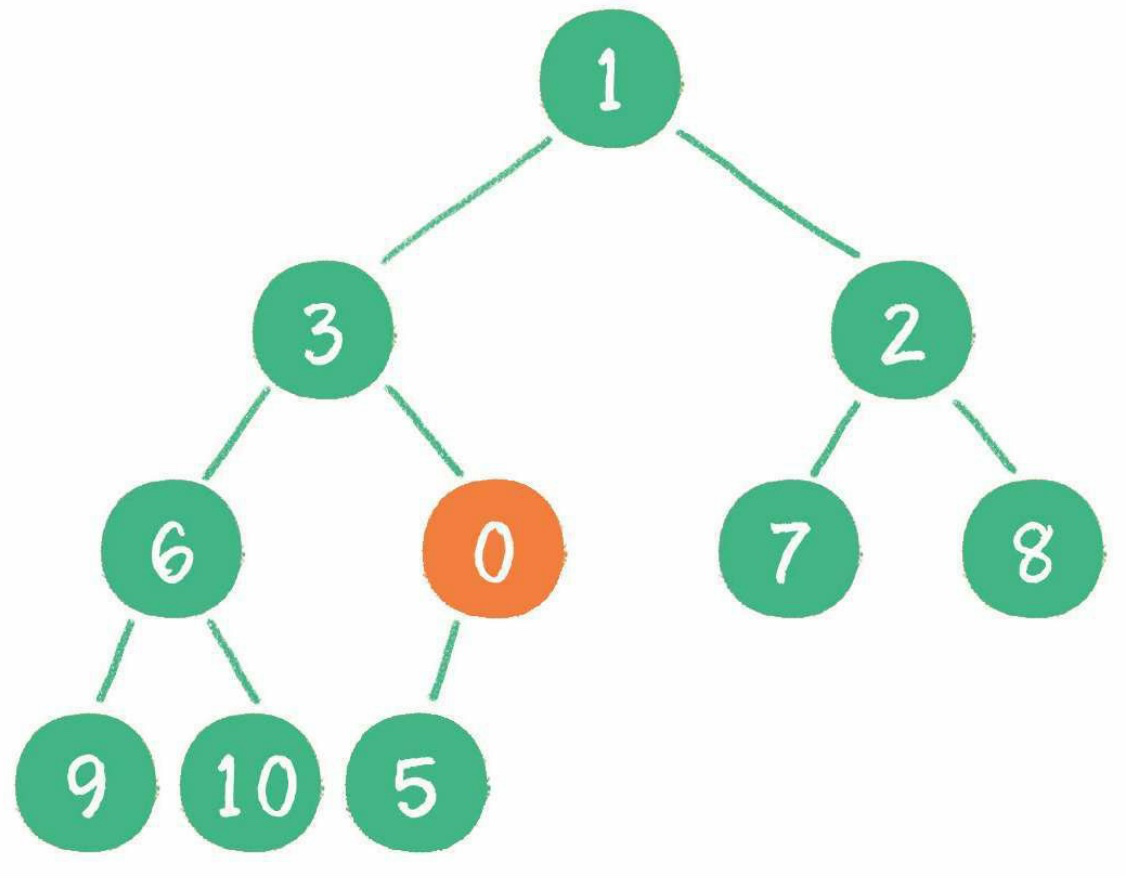
如,插入0:
1. 插入到最后

2. 和父節點比較并上浮
3. 和父節點比較并上浮
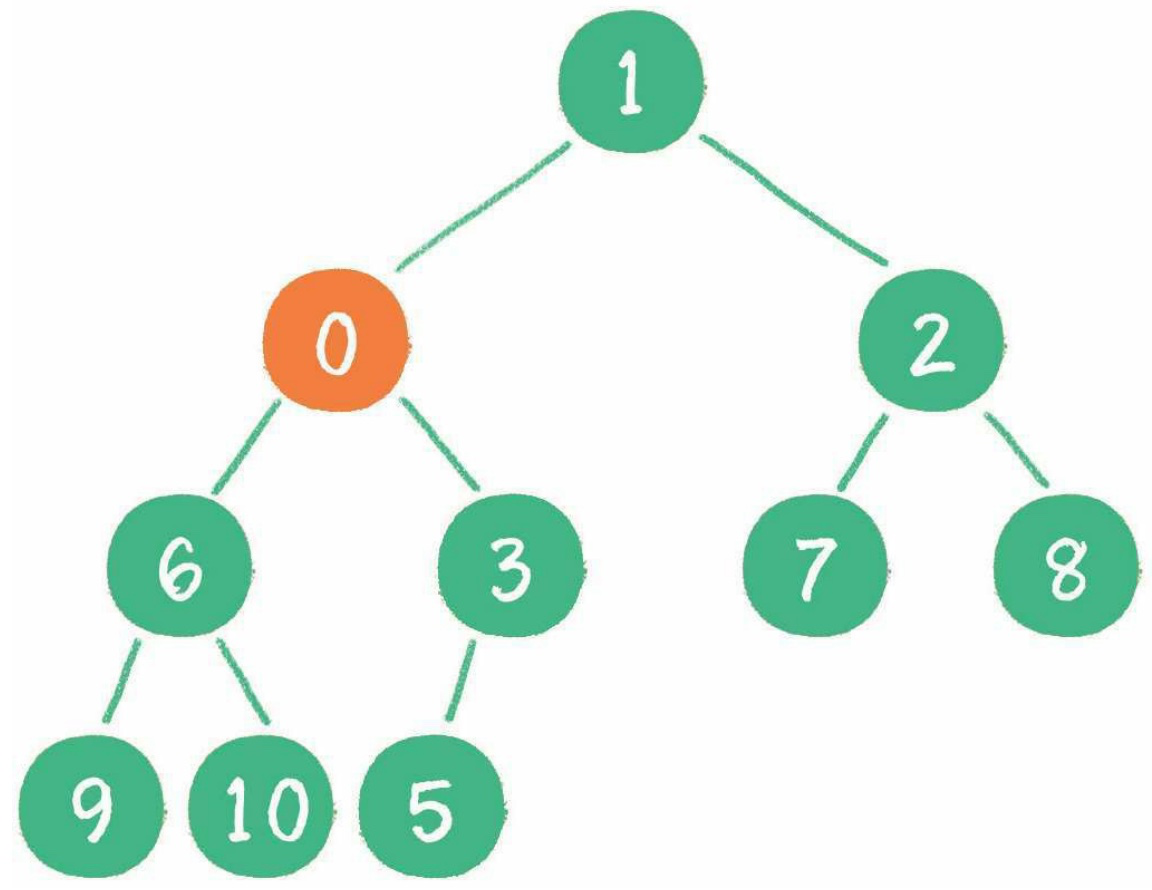
4. 繼續比較上浮
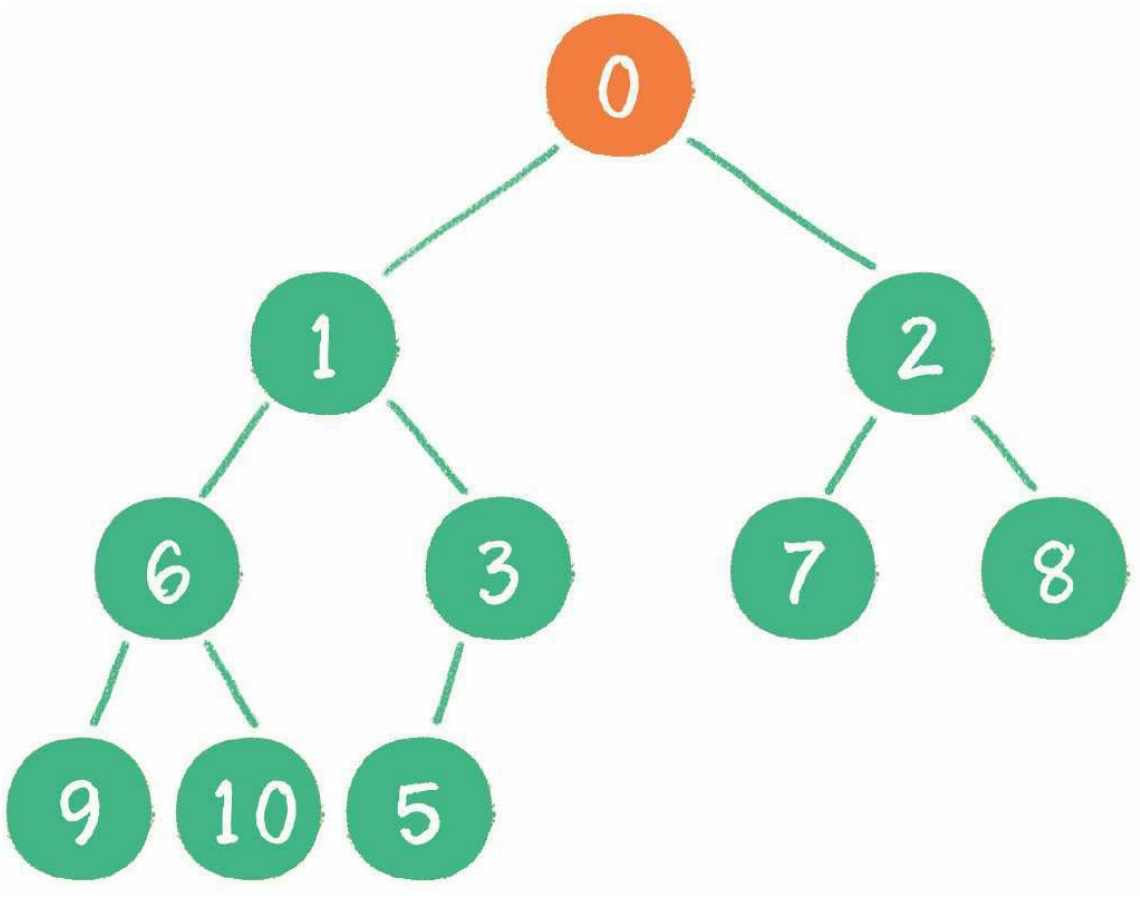
## 刪除節點
刪除節點時,一般就是刪除堆是根節點,過程和插入節點正好相反:
1. 刪除頂節點
2. 將最后一個節點拿到父節點
3. 和子節點比較并 `下沉`
比如,刪除 1
1. 刪除節點
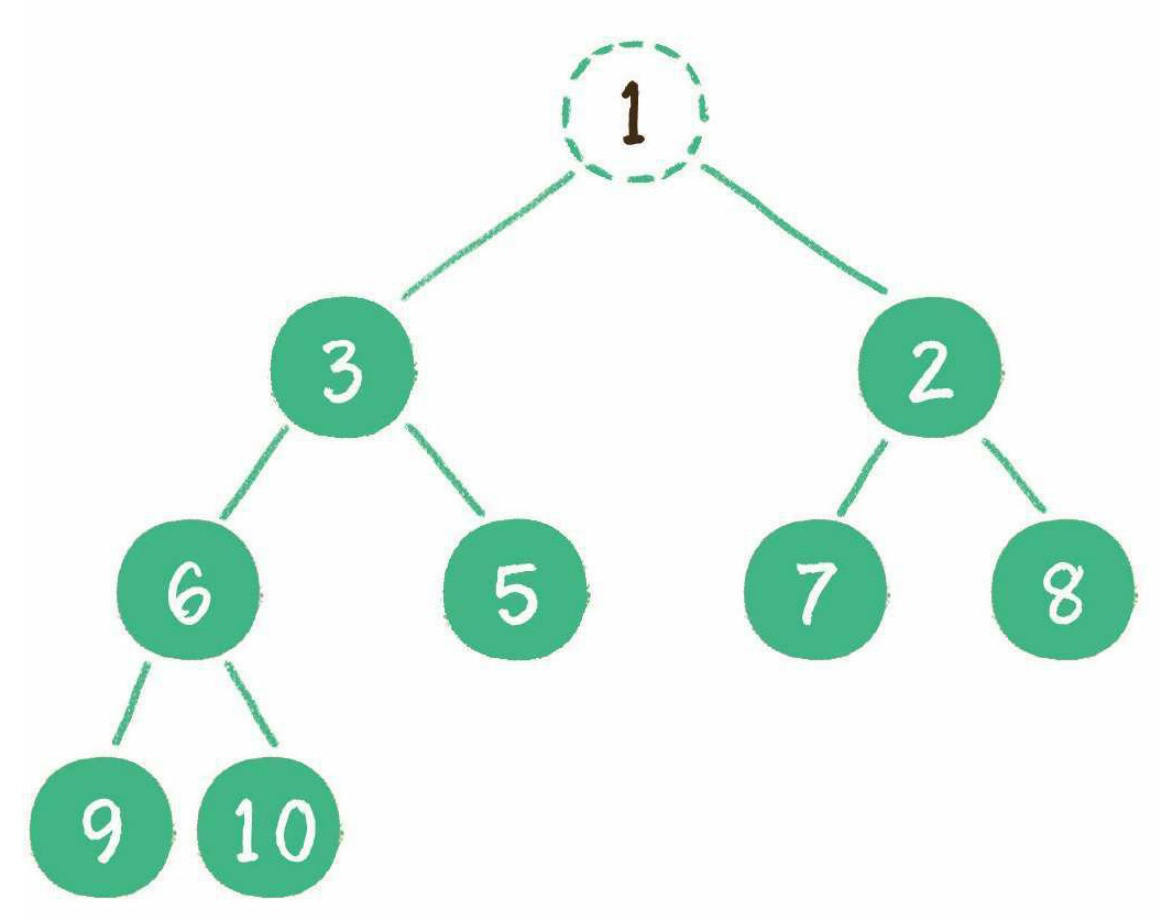
2. 將最后一個節點臨時拿到根節點的位置

3. 和左右子節點比較,讓最小的節點上來,它下沉
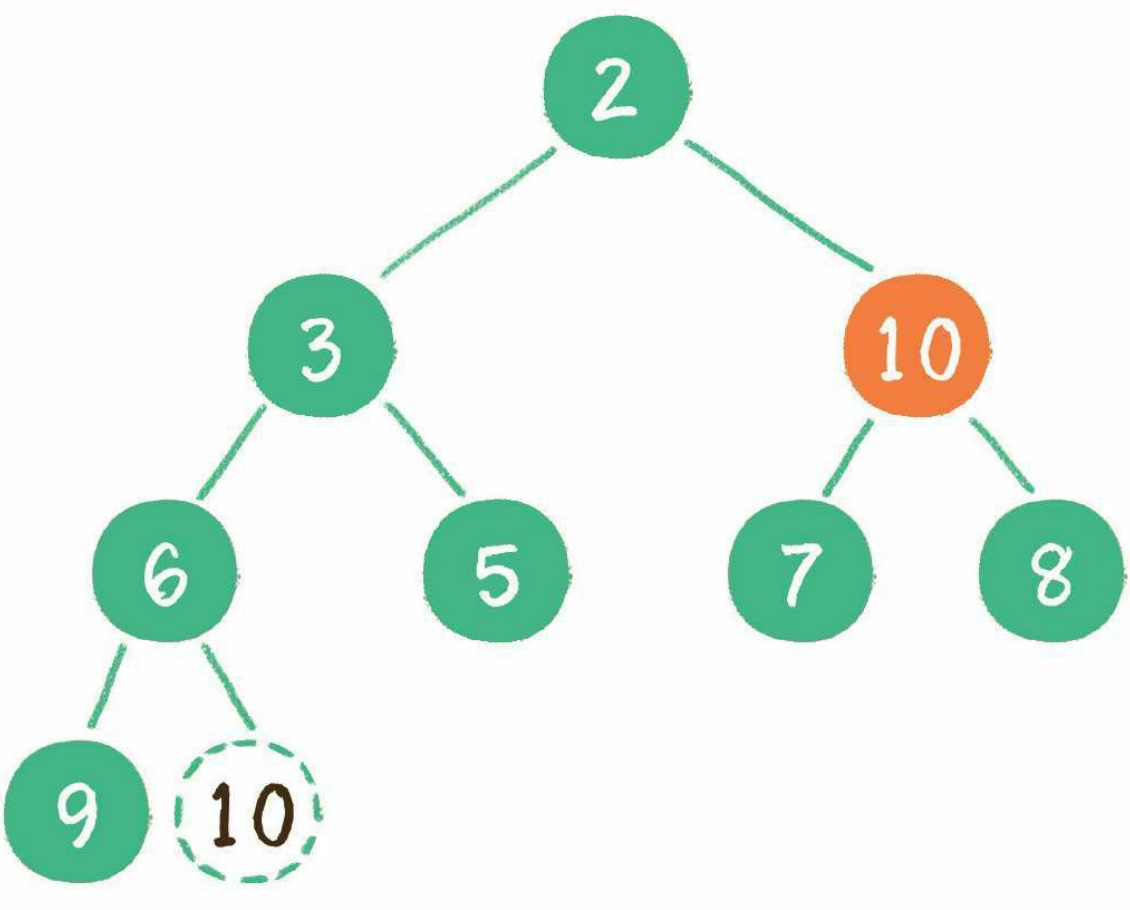
4. 繼續和子節點比較并下沉
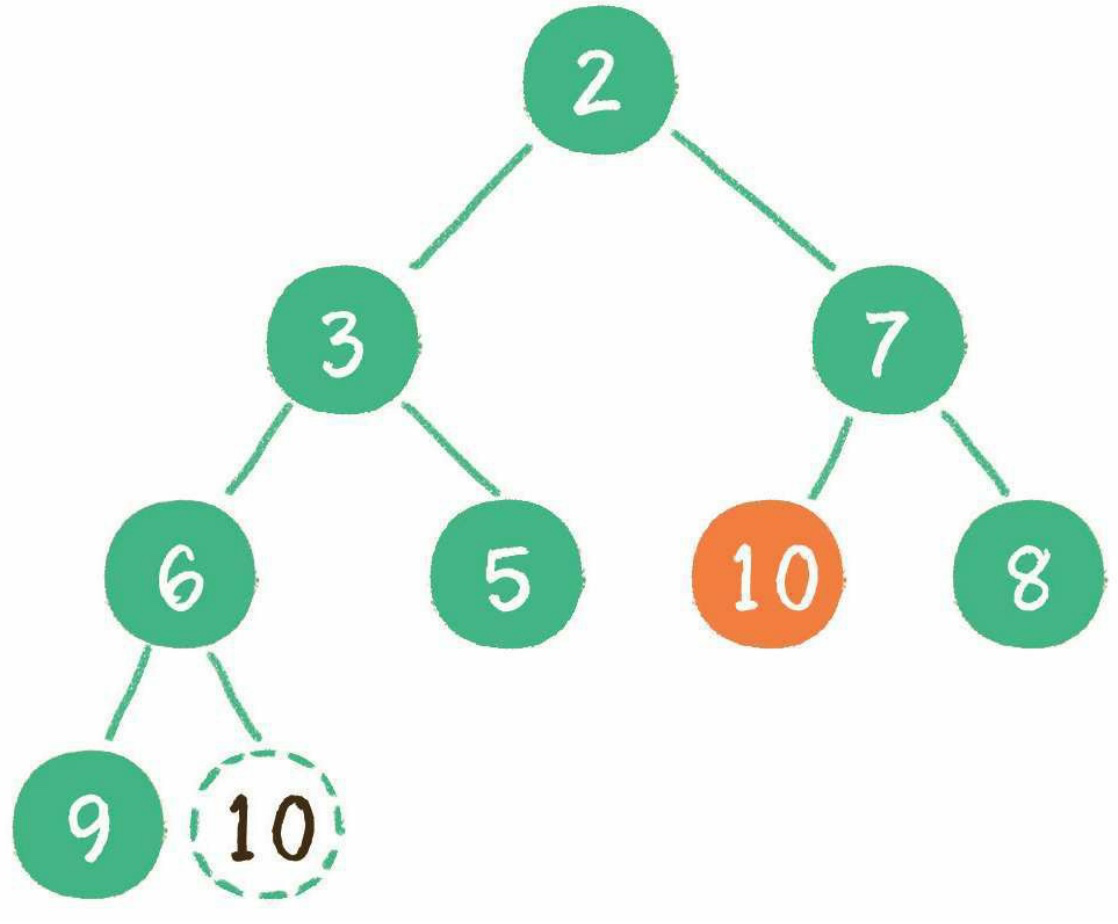
## 構建二叉堆
[排序](%E6%8E%92%E5%BA%8F.md)從最后一個 `非葉子節點 Math.floor(數組長度/2)-1` 開始比較并 (大/小)上浮。
1. 比較有以下堆
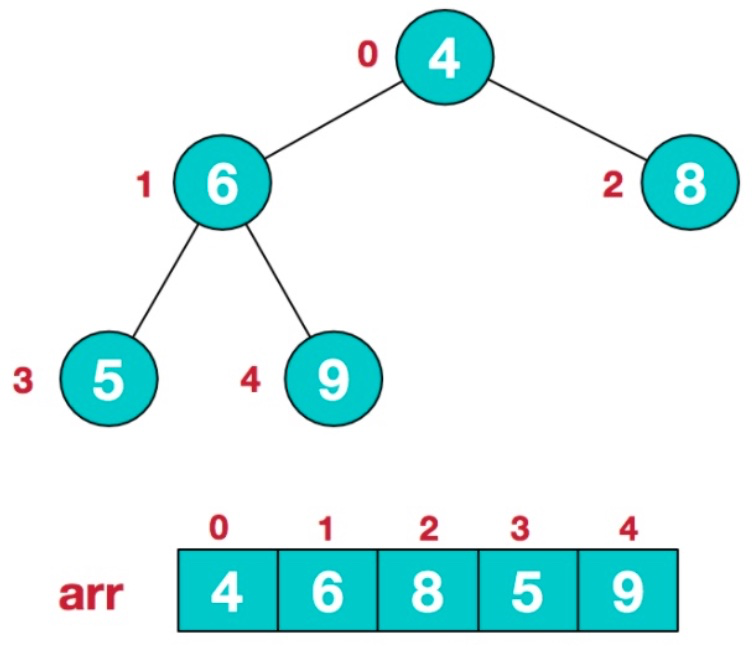
2. 從最后一個非葉子節點開始比較
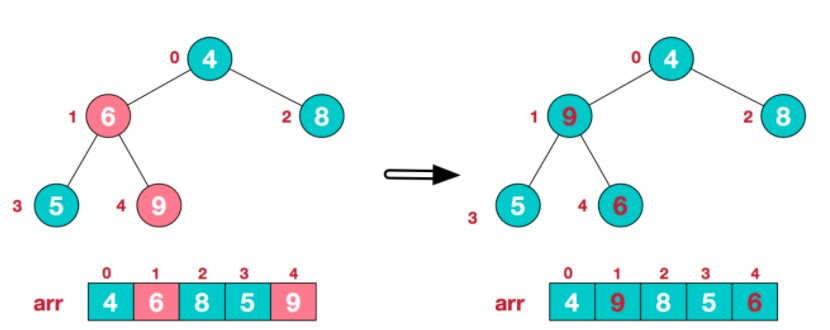
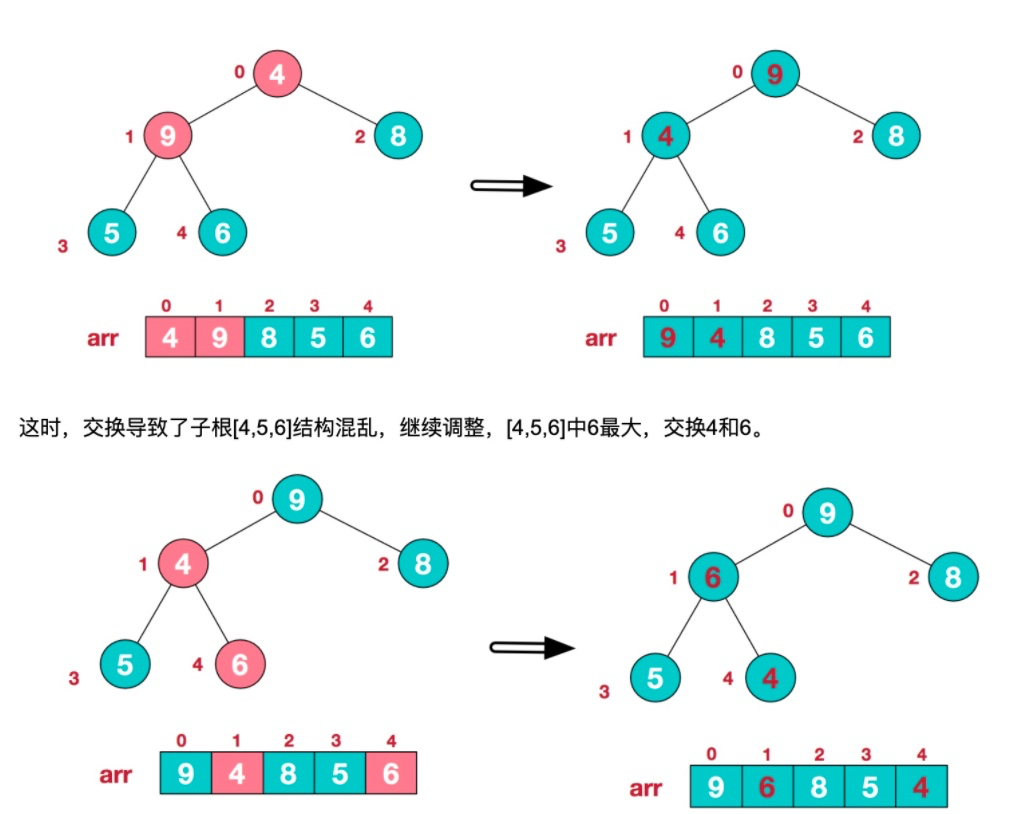
# 代碼實現
~~~
// 小頂堆
class SmallHeap {
constructor() {
// 初始化一個保存數據的數組
this.arr = []
}
// 向堆中放數據
push(data) {
// 1. 先將數據放到堆尾
this.arr.push(data)
// 2. 上浮(依次和父節點進行比較)
// 2.1 獲取當前這個新元素的下標
let current = this.arr.length - 1
// 2.2 父元素的下標
let parent = Math.floor((current - 1) / 2)
// 2.3 循環一直找父節點
while (parent >= 0) {
// 2.4 和父節點比較
if (this.arr[current] < this.arr[parent]) {
// 2.5 交換
[this.arr[current], this.arr[parent]] = [this.arr[parent], this.arr[current]]
// 2.6 當前節點的下標變成父節點的下標
current = parent
// 2.7 重新計算新的父節點
parent = Math.floor((current - 1) / 2)
} else {
// 2.8 如果當前節點大就退出循環
break
}
}
}
// 彈出堆頂元素
pop() {
// 1. 獲取堆頂元素的值
let value = this.arr[0]
// 2. 獲取數組中最后一個元素的值,并將這個值從數組中刪除
let lastValue = this.arr.pop()
// 3. 最后一個值替換第1個元素
this.arr[0] = lastValue
// 4. 和子節點比較然后進行下沉
// 4.1 當前節點的下標
let current = 0
// 4.2 左、右子節點的下標
let left = 2 * current + 1
let right = 2 * current + 2
let smallest = 0 // 最小元素的下標
// 如果有子節點就向下比較
while (left < this.arr.length) {
// 4.3 比左子節點大
if (this.arr[current] > this.arr[left]) {
// 左子節點和右子節點的大小
if (this.arr[left] > this.arr[right]) {
// 右邊最小
smallest = right
} else {
// 左邊最小
smallest = left
}
} else {
// 當前節點小于左子節點
// 判斷和右子節點的大小
if (this.arr[current] <= this.arr[right]) {
// 退出循環
break
} else {
smallest = right
}
}
// 最小元素的下標和當前元素下標是否相等
if (current === smallest) {
break
} else {
// 當前元素和最小元素進行交換
[this.arr[current], this.arr[smallest]] = [this.arr[smallest], this.arr[current]]
// 修改相關下標
current = smallest // 當前下標變成交換之后最小的下標
// 重新計算左右子節點下標
left = 2 * current + 1
right = 2 * current + 2
}
}
return value
}
}
let smH = new SmallHeap()
smH.push(10)
smH.push(5)
smH.push(2)
smH.push(8)
smH.push(1)
smH.push(4)
console.log(smH.arr)
console.log(smH.pop())
console.log(smH.arr)
~~~
