3.1 Python中的統計學 · SciPy Lecture Notes 中文版

# 3.1 Python中的統計學 In?[1]: ``` %matplotlib inline import numpy as np ``` > **作者** : Ga?l Varoquaux **必要條件** * 標準Python科學計算環境 (numpy, scipy, matplotlib) * [Pandas](http://pandas.pydata.org/) * [Statsmodels](http://statsmodels.sourceforge.net/) * [Seaborn](http://stanford.edu/~mwaskom/software/seaborn/) 要安裝Python及這些依賴，推薦下載[Anaconda Python](http://continuum.io/downloads) 或 [Enthought Canopy](https://store.enthought.com/), 如果你使用Ubuntu或其他linux更應該使用包管理器。 **也可以看一下: Python中的貝葉斯統計** 本章并不會涉及貝葉斯統計工具。適用于貝葉斯模型的是[PyMC](http://pymc-devs.github.io/pymc), 在Python中實現了概率編程語言。 **為什么統計學要用Python?** R是一門專注于統計學的語言。Python是帶有統計學模塊的通用編程語言。R比Python有更多的統計分析功能，以及專用的語法。但是，當面對構建復雜的分析管道，混合統計學以及例如圖像分析、文本挖掘或者物理實驗控制，Python的富有就是物價的優勢。 **內容** * 數據表征和交互 * 數據作為表格 * panda data-frame * 假設檢驗: 對比兩個組 * Student’s t-test: 最簡單的統計檢驗 * 配對實驗: 對同一個體的重復測量 * 線性模型、多因素和方差分析 * 用“公式” 來在Python中指定統計模型 * 多元回歸: 包含多元素 * 事后假設檢驗: 方差分析 (ANOVA) * 更多的可視化: 用seaborn來進行統計學探索 * 配對圖: 散點矩陣 * lmplot: 繪制一個單變量回歸 * 交互作用檢驗 **免責聲明: 性別問題** 本教程中的一些實例選自性別問題。其原因是在這種問題上這種控制的聲明實際上影響了很多人。 ## 3.1.1 數據表征和交互 ### 3.1.1.1 數據作為表格統計分析中我們關注的設定是通過一組不同的屬性或特征來描述多個觀察或樣本。然后這個數據可以被視為2D表格，或矩陣，列是數據的不同屬性，行是觀察。例如包含在[examples/brain_size.csv](http://www.scipy-lectures.org/_downloads/brain_size.csv)的數據: `"";"Gender";"FSIQ";"VIQ";"PIQ";"Weight";"Height";"MRI_Count" "1";"Female";133;132;124;"118";"64.5";816932 "2";"Male";140;150;124;".";"72.5";1001121 "3";"Male";139;123;150;"143";"73.3";1038437 "4";"Male";133;129;128;"172";"68.8";965353 "5";"Female";137;132;134;"147";"65.0";951545` ### 3.1.1.2 panda data-frame 我們將會在來自[pandas](http://pandas.pydata.org/)模塊的[pandas.DataFrame](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html#pandas.DataFrame)中存儲和操作這個數據。它是電子表格程序在Python中的一個等價物。它與2D `numpy`數據的區別在于列帶有名字，可以在列中存儲混合的數據類型，并且有精妙的選擇和透視表機制。 #### 3.1.1.2.1 創建dataframes: 讀取數據文件或轉化數組 **從CSV文件讀取**: 使用上面的CSV文件，給出了大腦大小重量和IQ (Willerman et al. 1991) 的觀察值 , 數據混合了數量值和類型值: In?[3]: ``` import pandas data = pandas.read_csv('examples/brain_size.csv', sep=';', na_values=".") data ``` Out[3]: | | Unnamed: 0 | Gender | FSIQ | VIQ | PIQ | Weight | Height | MRI_Count | | --- | --- | --- | --- | --- | --- | --- | --- | --- | | 0 | 1 | Female | 133 | 132 | 124 | 118 | 64.5 | 816932 | | 1 | 2 | Male | 140 | 150 | 124 | NaN | 72.5 | 1001121 | | 2 | 3 | Male | 139 | 123 | 150 | 143 | 73.3 | 1038437 | | 3 | 4 | Male | 133 | 129 | 128 | 172 | 68.8 | 965353 | | 4 | 5 | Female | 137 | 132 | 134 | 147 | 65.0 | 951545 | | 5 | 6 | Female | 99 | 90 | 110 | 146 | 69.0 | 928799 | | 6 | 7 | Female | 138 | 136 | 131 | 138 | 64.5 | 991305 | | 7 | 8 | Female | 92 | 90 | 98 | 175 | 66.0 | 854258 | | 8 | 9 | Male | 89 | 93 | 84 | 134 | 66.3 | 904858 | | 9 | 10 | Male | 133 | 114 | 147 | 172 | 68.8 | 955466 | | 10 | 11 | Female | 132 | 129 | 124 | 118 | 64.5 | 833868 | | 11 | 12 | Male | 141 | 150 | 128 | 151 | 70.0 | 1079549 | | 12 | 13 | Male | 135 | 129 | 124 | 155 | 69.0 | 924059 | | 13 | 14 | Female | 140 | 120 | 147 | 155 | 70.5 | 856472 | | 14 | 15 | Female | 96 | 100 | 90 | 146 | 66.0 | 878897 | | 15 | 16 | Female | 83 | 71 | 96 | 135 | 68.0 | 865363 | | 16 | 17 | Female | 132 | 132 | 120 | 127 | 68.5 | 852244 | | 17 | 18 | Male | 100 | 96 | 102 | 178 | 73.5 | 945088 | | 18 | 19 | Female | 101 | 112 | 84 | 136 | 66.3 | 808020 | | 19 | 20 | Male | 80 | 77 | 86 | 180 | 70.0 | 889083 | | 20 | 21 | Male | 83 | 83 | 86 | NaN | NaN | 892420 | | 21 | 22 | Male | 97 | 107 | 84 | 186 | 76.5 | 905940 | | 22 | 23 | Female | 135 | 129 | 134 | 122 | 62.0 | 790619 | | 23 | 24 | Male | 139 | 145 | 128 | 132 | 68.0 | 955003 | | 24 | 25 | Female | 91 | 86 | 102 | 114 | 63.0 | 831772 | | 25 | 26 | Male | 141 | 145 | 131 | 171 | 72.0 | 935494 | | 26 | 27 | Female | 85 | 90 | 84 | 140 | 68.0 | 798612 | | 27 | 28 | Male | 103 | 96 | 110 | 187 | 77.0 | 1062462 | | 28 | 29 | Female | 77 | 83 | 72 | 106 | 63.0 | 793549 | | 29 | 30 | Female | 130 | 126 | 124 | 159 | 66.5 | 866662 | | 30 | 31 | Female | 133 | 126 | 132 | 127 | 62.5 | 857782 | | 31 | 32 | Male | 144 | 145 | 137 | 191 | 67.0 | 949589 | | 32 | 33 | Male | 103 | 96 | 110 | 192 | 75.5 | 997925 | | 33 | 34 | Male | 90 | 96 | 86 | 181 | 69.0 | 879987 | | 34 | 35 | Female | 83 | 90 | 81 | 143 | 66.5 | 834344 | | 35 | 36 | Female | 133 | 129 | 128 | 153 | 66.5 | 948066 | | 36 | 37 | Male | 140 | 150 | 124 | 144 | 70.5 | 949395 | | 37 | 38 | Female | 88 | 86 | 94 | 139 | 64.5 | 893983 | | 38 | 39 | Male | 81 | 90 | 74 | 148 | 74.0 | 930016 | | 39 | 40 | Male | 89 | 91 | 89 | 179 | 75.5 | 935863 | > **分割符** 它是CSV文件，但是分割符是”;” > > **缺失值** CSV中的第二個個體的weight是缺失的。如果我們沒有指定缺失值 (NA = not available) 標記符, 我們將無法進行統計分析。 **從數組中創建**: [pandas.DataFrame](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html#pandas.DataFrame) 也可以視為1D序列, 例如數組或列表的字典，如果我們有3個`numpy`數組: In?[4]: ``` import numpy as np t = np.linspace(-6, 6, 20) sin_t = np.sin(t) cos_t = np.cos(t) ``` 我們可以將他們暴露為[pandas.DataFrame](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html#pandas.DataFrame): In?[5]: ``` pandas.DataFrame({'t': t, 'sin': sin_t, 'cos': cos_t}) ``` Out[5]: | | cos | sin | t | | --- | --- | --- | --- | | 0 | 0.960170 | 0.279415 | -6.000000 | | 1 | 0.609977 | 0.792419 | -5.368421 | | 2 | 0.024451 | 0.999701 | -4.736842 | | 3 | -0.570509 | 0.821291 | -4.105263 | | 4 | -0.945363 | 0.326021 | -3.473684 | | 5 | -0.955488 | -0.295030 | -2.842105 | | 6 | -0.596979 | -0.802257 | -2.210526 | | 7 | -0.008151 | -0.999967 | -1.578947 | | 8 | 0.583822 | -0.811882 | -0.947368 | | 9 | 0.950551 | -0.310567 | -0.315789 | | 10 | 0.950551 | 0.310567 | 0.315789 | | 11 | 0.583822 | 0.811882 | 0.947368 | | 12 | -0.008151 | 0.999967 | 1.578947 | | 13 | -0.596979 | 0.802257 | 2.210526 | | 14 | -0.955488 | 0.295030 | 2.842105 | | 15 | -0.945363 | -0.326021 | 3.473684 | | 16 | -0.570509 | -0.821291 | 4.105263 | | 17 | 0.024451 | -0.999701 | 4.736842 | | 18 | 0.609977 | -0.792419 | 5.368421 | | 19 | 0.960170 | -0.279415 | 6.000000 | **其他輸入**: [pandas](http://pandas.pydata.org/) 可以從SQL、excel文件或者其他格式輸入數。見[pandas文檔](http://pandas.pydata.org/)。 #### 3.1.1.2.2 操作數據 `data`是[pandas.DataFrame](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html#pandas.DataFrame), 與R的dataframe類似: In?[6]: ``` data.shape # 40行8列 ``` Out[6]: ``` (40, 8) ``` In?[7]: ``` data.columns # 有列 ``` Out[7]: ``` Index([u'Unnamed: 0', u'Gender', u'FSIQ', u'VIQ', u'PIQ', u'Weight', u'Height', u'MRI_Count'], dtype='object') ``` In?[8]: ``` print(data['Gender']) # 列可以用名字訪問 ``` ``` 0 Female 1 Male 2 Male 3 Male 4 Female 5 Female 6 Female 7 Female 8 Male 9 Male 10 Female 11 Male 12 Male 13 Female 14 Female 15 Female 16 Female 17 Male 18 Female 19 Male 20 Male 21 Male 22 Female 23 Male 24 Female 25 Male 26 Female 27 Male 28 Female 29 Female 30 Female 31 Male 32 Male 33 Male 34 Female 35 Female 36 Male 37 Female 38 Male 39 Male Name: Gender, dtype: object ``` In?[9]: ``` # 簡單選擇器 data[data['Gender'] == 'Female']['VIQ'].mean() ``` Out[9]: ``` 109.45 ``` > **注意**: 對于一個大dataframe的快速預覽，用它的`describe`方法: [pandas.DataFrame.describe()](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.describe.html#pandas.DataFrame.describe)。 **groupby**: 根據類別變量的值拆分dataframe: In?[10]: ``` groupby_gender = data.groupby('Gender') for gender, value in groupby_gender['VIQ']: print((gender, value.mean())) ``` ``` ('Female', 109.45) ('Male', 115.25) ``` **groupby_gender**是一個強力的對象，暴露了結果dataframes組的許多操作: In?[11]: ``` groupby_gender.mean() ``` Out[11]: | | Unnamed: 0 | FSIQ | VIQ | PIQ | Weight | Height | MRI_Count | | --- | --- | --- | --- | --- | --- | --- | --- | | Gender | | Female | 19.65 | 111.9 | 109.45 | 110.45 | 137.200000 | 65.765000 | 862654.6 | | Male | 21.35 | 115.0 | 115.25 | 111.60 | 166.444444 | 71.431579 | 954855.4 | 在`groupby_gender`上使用tab-完成來查找更多。其他的常見分組函數是median, count (對于檢查不同子集的缺失值數量很有用) 或sum。Groupby評估是懶惰模式，因為在應用聚合函數之前不會進行什么工作。 > **練習** > > * 完整人口VIO的平均值是多少? > * 這項研究中包含了多少男性 / 女性? > * **提示** 使用‘tab完成’來尋找可以調用的方法, 替換在上面例子中的‘mean’。 > * 對于男性和女性來說，以log為單位顯示的MRI count平均值是多少? ![](http://www.scipy-lectures.org/_images/plot_pandas_1.png) > **注意**: 上面的繪圖中使用了`groupby_gender.boxplot` (見[這個例子](http://www.scipy-lectures.org/packages/statistics/auto_examples/plot_pandas.html#example-plot-pandas-py))。 #### 3.1.1.2.3 繪制數據 Pandas提供一些繪圖工具 (`pandas.tools.plotting`, 后面使用的是matplotlib) 來顯示在dataframes數據的統計值: **散點圖矩陣**: In?[15]: ``` from pandas.tools import plotting plotting.scatter_matrix(data[['Weight', 'Height', 'MRI_Count']]) ``` Out[15]: ``` array([[<matplotlib.axes._subplots.AxesSubplot object at 0x105c34810>, <matplotlib.axes._subplots.AxesSubplot object at 0x10a0ade10>, <matplotlib.axes._subplots.AxesSubplot object at 0x10a2d80d0>], [<matplotlib.axes._subplots.AxesSubplot object at 0x10a33b210>, <matplotlib.axes._subplots.AxesSubplot object at 0x10a3be450>, <matplotlib.axes._subplots.AxesSubplot object at 0x10a40d9d0>], [<matplotlib.axes._subplots.AxesSubplot object at 0x10a49dc10>, <matplotlib.axes._subplots.AxesSubplot object at 0x10a51f850>, <matplotlib.axes._subplots.AxesSubplot object at 0x10a5902d0>]], dtype=object) ``` ``` /Library/Frameworks/Python.framework/Versions/2.7/lib/python2.7/site-packages/matplotlib/collections.py:590: FutureWarning: elementwise comparison failed; returning scalar instead, but in the future will perform elementwise comparison if self._edgecolors == str('face'): ``` ![](https://box.kancloud.cn/2016-03-21_56efdc0bacd40.png) In?[16]: ``` plotting.scatter_matrix(data[['PIQ', 'VIQ', 'FSIQ']]) ``` Out[16]: ``` array([[<matplotlib.axes._subplots.AxesSubplot object at 0x10a918b50>, <matplotlib.axes._subplots.AxesSubplot object at 0x10aa38710>, <matplotlib.axes._subplots.AxesSubplot object at 0x10ab29910>], [<matplotlib.axes._subplots.AxesSubplot object at 0x10ab8e790>, <matplotlib.axes._subplots.AxesSubplot object at 0x10ae207d0>, <matplotlib.axes._subplots.AxesSubplot object at 0x10abbd090>], [<matplotlib.axes._subplots.AxesSubplot object at 0x10af140d0>, <matplotlib.axes._subplots.AxesSubplot object at 0x10af89cd0>, <matplotlib.axes._subplots.AxesSubplot object at 0x10affa410>]], dtype=object) ``` ![](https://box.kancloud.cn/2016-03-21_56efdc0bc1aeb.png) > **兩個總體** > > IQ指標是雙峰的, 似乎有兩個子總體。 > > **練習** > > 只繪制男性的散點圖矩陣，然后是只有女性的。你是否認為2個子總體與性別相關? ## 3.1.2 假設檢驗: 比較兩個組對于簡單的[統計檢驗](https://en.wikipedia.org/wiki/Statistical_hypothesis_testing)，我們將可以使用[scipy](http://docs.scipy.org/doc/)的子摸塊[scipy.stats](http://docs.scipy.org/doc/scipy/reference/stats.html#module-scipy.stats): In?[17]: ``` from scipy import stats ``` > **也看一下**: Scipy是一個很大的庫。關于整個庫的快速預覽，可以看一下[scipy](http://nbviewer.ipython.org/github/cloga/scipy-lecture-notes_cn/blob/master/1.5.%20Scipy%EF%BC%9A%E9%AB%98%E7%BA%A7%E7%A7%91%E5%AD%A6%E8%AE%A1%E7%AE%97.ipynb) 章節。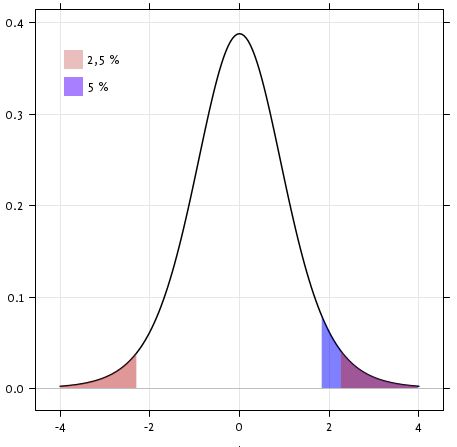 ### 3.1.2.1 Student’s t檢驗: 最簡單的統計檢驗 #### 3.1.2.1.1 單樣本 t-檢驗: 檢驗總體平均數的值 [scipy.stats.ttest_1samp()](http://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_1samp.html#scipy.stats.ttest_1samp)檢驗數據總體的平均數是否可能等于給定值 (嚴格來說是否觀察值來自于給定總體平均數的正態分布)。它返回一個[T統計值](https://en.wikipedia.org/wiki/Student%27s_t-test)以及[p-值](https://en.wikipedia.org/wiki/P-value) (見函數的幫助): In?[18]: ``` stats.ttest_1samp(data['VIQ'], 0) ``` Out[18]: ``` (30.088099970849328, 1.3289196468728067e-28) ``` 根據$10^-28$的p-值，我們可以聲稱IQ(VIQ的測量值)總體平均數不是0。 ![](http://www.scipy-lectures.org/_images/two_sided.png) #### 3.1.2.1.2 雙樣本 t-檢驗: 檢驗不同總體的差異我們已經看到男性和女性總體VIQ平均數是不同的。要檢驗這個差異是否是顯著的，我們可以用[scipy.stats.ttest_ind()](http://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.ttest_ind.html#scipy.stats.ttest_ind)進行雙樣本檢驗: In?[19]: ``` female_viq = data[data['Gender'] == 'Female']['VIQ'] male_viq = data[data['Gender'] == 'Male']['VIQ'] stats.ttest_ind(female_viq, male_viq) ``` Out[19]: ``` (-0.77261617232750113, 0.44452876778583217) ``` ### 3.1.2.2 配對實驗: 同一個體的重復測量 PIQ、VIQ和FSIQ給出了IQ的3種測量值。讓我檢驗一下FISQ和PIQ是否有顯著差異。我們可以使用雙樣本檢驗: In?[20]: ``` stats.ttest_ind(data['FSIQ'], data['PIQ']) ``` Out[20]: ``` (0.46563759638096403, 0.64277250094148408) ``` 使用這種方法的問題是忘記了兩個觀察之間有聯系: FSIQ 和 PIQ 是在相同的個體上進行的測量。因此被試之間的差異是混淆的，并且可以使用"配對實驗"或"[重復測量實驗](https://en.wikipedia.org/wiki/Repeated_measures_design)"來消除。 In?[21]: ``` stats.ttest_rel(data['FSIQ'], data['PIQ']) ``` Out[21]: ``` (1.7842019405859857, 0.082172638183642358) ``` ![](http://www.scipy-lectures.org/_images/plot_paired_boxplots_1.png) 這等價于單樣本的差異檢驗: In?[22]: ``` stats.ttest_1samp(data['FSIQ'] - data['PIQ'], 0) ``` Out[22]: ``` (1.7842019405859857, 0.082172638183642358) ``` ![](http://www.scipy-lectures.org/_images/plot_paired_boxplots_2.png) T-tests假定高斯誤差。我們可以使用[威爾科克森符號秩檢驗](https://en.wikipedia.org/wiki/Wilcoxon_signed-rank_test), 放松了這個假設: In?[23]: ``` stats.wilcoxon(data['FSIQ'], data['PIQ']) ``` Out[23]: ``` (274.5, 0.10659492713506856) ``` > **注意:** 非配對實驗對應的非參數檢驗是[曼惠特尼U檢驗](https://en.wikipedia.org/wiki/Mann%E2%80%93Whitney_U), [scipy.stats.mannwhitneyu()](http://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.mannwhitneyu.html#scipy.stats.mannwhitneyu)。 > > **練習** > > * 檢驗男性和女性重量的差異。 > * 使用非參數檢驗來檢驗男性和女性VIQ的差異。 > > **結論**: 我們發現數據并不支持男性和女性VIQ不同的假設。 ## 3.1.3 線性模型、多因素和因素分析 ### 3.1.3.1 用“公式” 來在Python中指定統計模型 #### 3.1.3.1.1 簡單線性回歸給定兩組觀察值，x和y, 我們想要檢驗假設y是x的線性函數，換句話說: $y = x * coef + intercept + e$ 其中$e$是觀察噪音。我們將使用[statmodels module](http://statsmodels.sourceforge.net/): * 擬合一個線性模型。我們將使用簡單的策略，[普通最小二乘](https://en.wikipedia.org/wiki/Ordinary_least_squares) (OLS)。 * 檢驗系數是否是非0。 ![](http://www.scipy-lectures.org/_images/plot_regression_1.png) 首先，我們生成模型的虛擬數據: In?[9]: ``` import numpy as np x = np.linspace(-5, 5, 20) np.random.seed(1) # normal distributed noise y = -5 + 3*x + 4 * np.random.normal(size=x.shape) # Create a data frame containing all the relevant variables data = pandas.DataFrame({'x': x, 'y': y}) ``` > **Python中的統計公式** > > [見statsmodels文檔](http://statsmodels.sourceforge.net/stable/example_formulas.html) 然后我們指定一個OLS模型并且擬合它: In?[10]: ``` from statsmodels.formula.api import ols model = ols("y ~ x", data).fit() ``` 我們可以檢查fit產生的各種統計量: In?[26]: ``` print(model.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: y R-squared: 0.804 Model: OLS Adj. R-squared: 0.794 Method: Least Squares F-statistic: 74.03 Date: Wed, 18 Nov 2015 Prob (F-statistic): 8.56e-08 Time: 17:10:03 Log-Likelihood: -57.988 No. Observations: 20 AIC: 120.0 Df Residuals: 18 BIC: 122.0 Df Model: 1 Covariance Type: nonrobust ============================================================================== coef std err t P>|t| [95.0% Conf. Int.] ------------------------------------------------------------------------------ Intercept -5.5335 1.036 -5.342 0.000 -7.710 -3.357 x 2.9369 0.341 8.604 0.000 2.220 3.654 ============================================================================== Omnibus: 0.100 Durbin-Watson: 2.956 Prob(Omnibus): 0.951 Jarque-Bera (JB): 0.322 Skew: -0.058 Prob(JB): 0.851 Kurtosis: 2.390 Cond. No. 3.03 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` > **術語**: > > Statsmodels使用統計術語: statsmodel的y變量被稱為‘endogenous’而x變量被稱為exogenous。更詳細的討論見[這里](http://statsmodels.sourceforge.net/devel/endog_exog.html)。 > > 為了簡化，y (endogenous) 是你要嘗試預測的值，而 x (exogenous) 代表用來進行這個預測的特征。 > > **練習** > > 從以上模型中取回估計參數。**提示**: 使用tab-完成來找到相關的屬性。 #### 3.1.3.1.2 類別變量: 比較組或多個類別讓我們回到大腦大小的數據: In?[27]: ``` data = pandas.read_csv('examples/brain_size.csv', sep=';', na_values=".") ``` 我們可以寫一個比較，用線性模型比較男女IQ: In?[28]: ``` model = ols("VIQ ~ Gender + 1", data).fit() print(model.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: VIQ R-squared: 0.015 Model: OLS Adj. R-squared: -0.010 Method: Least Squares F-statistic: 0.5969 Date: Wed, 18 Nov 2015 Prob (F-statistic): 0.445 Time: 17:34:10 Log-Likelihood: -182.42 No. Observations: 40 AIC: 368.8 Df Residuals: 38 BIC: 372.2 Df Model: 1 Covariance Type: nonrobust ================================================================================== coef std err t P>|t| [95.0% Conf. Int.] ---------------------------------------------------------------------------------- Intercept 109.4500 5.308 20.619 0.000 98.704 120.196 Gender[T.Male] 5.8000 7.507 0.773 0.445 -9.397 20.997 ============================================================================== Omnibus: 26.188 Durbin-Watson: 1.709 Prob(Omnibus): 0.000 Jarque-Bera (JB): 3.703 Skew: 0.010 Prob(JB): 0.157 Kurtosis: 1.510 Cond. No. 2.62 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` **特定模型的提示** **強制類別**: ‘Gender’ 被自動識別為類別變量，因此，它的每一個不同值都被處理為不同的實體。使用: In?[29]: ``` model = ols('VIQ ~ C(Gender)', data).fit() ``` 可以將一個整數列強制作為類別處理。 **截距**: 我們可以在公式中用-1刪除截距，或者用+1強制使用截距。默認，statsmodel將帶有K和可能值的類別變量處理為K-1'虛擬變量' (最后一個水平被吸收到截距項中)。在絕大多數情況下，這都是很好的默認選擇 - 但是，為類別變量指定不同的編碼方式也是可以的 ([http://statsmodels.sourceforge.net/devel/contrasts.html)。](http://statsmodels.sourceforge.net/devel/contrasts.html)。) **FSIQ和PIQ差異的t-檢驗** 要比較不同類型的IQ，我們需要創建一個"長形式"的表格，用一個類別變量來標識IQ類型: In?[30]: ``` data_fisq = pandas.DataFrame({'iq': data['FSIQ'], 'type': 'fsiq'}) data_piq = pandas.DataFrame({'iq': data['PIQ'], 'type': 'piq'}) data_long = pandas.concat((data_fisq, data_piq)) print(data_long) ``` ``` iq type 0 133 fsiq 1 140 fsiq 2 139 fsiq 3 133 fsiq 4 137 fsiq 5 99 fsiq 6 138 fsiq 7 92 fsiq 8 89 fsiq 9 133 fsiq 10 132 fsiq 11 141 fsiq 12 135 fsiq 13 140 fsiq 14 96 fsiq 15 83 fsiq 16 132 fsiq 17 100 fsiq 18 101 fsiq 19 80 fsiq 20 83 fsiq 21 97 fsiq 22 135 fsiq 23 139 fsiq 24 91 fsiq 25 141 fsiq 26 85 fsiq 27 103 fsiq 28 77 fsiq 29 130 fsiq .. ... ... 10 124 piq 11 128 piq 12 124 piq 13 147 piq 14 90 piq 15 96 piq 16 120 piq 17 102 piq 18 84 piq 19 86 piq 20 86 piq 21 84 piq 22 134 piq 23 128 piq 24 102 piq 25 131 piq 26 84 piq 27 110 piq 28 72 piq 29 124 piq 30 132 piq 31 137 piq 32 110 piq 33 86 piq 34 81 piq 35 128 piq 36 124 piq 37 94 piq 38 74 piq 39 89 piq [80 rows x 2 columns] ``` In?[31]: ``` model = ols("iq ~ type", data_long).fit() print(model.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: iq R-squared: 0.003 Model: OLS Adj. R-squared: -0.010 Method: Least Squares F-statistic: 0.2168 Date: Wed, 18 Nov 2015 Prob (F-statistic): 0.643 Time: 18:16:40 Log-Likelihood: -364.35 No. Observations: 80 AIC: 732.7 Df Residuals: 78 BIC: 737.5 Df Model: 1 Covariance Type: nonrobust =============================================================================== coef std err t P>|t| [95.0% Conf. Int.] ------------------------------------------------------------------------------- Intercept 113.4500 3.683 30.807 0.000 106.119 120.781 type[T.piq] -2.4250 5.208 -0.466 0.643 -12.793 7.943 ============================================================================== Omnibus: 164.598 Durbin-Watson: 1.531 Prob(Omnibus): 0.000 Jarque-Bera (JB): 8.062 Skew: -0.110 Prob(JB): 0.0178 Kurtosis: 1.461 Cond. No. 2.62 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` 我們可以看到我們獲得了與前面t-檢驗相同的值，以及相同的對應iq type的p-值: In?[32]: ``` stats.ttest_ind(data['FSIQ'], data['PIQ']) ``` Out[32]: ``` (0.46563759638096403, 0.64277250094148408) ``` ### 3.1.3.2 多元回歸: 包含多因素考慮用2個變量x和y來解釋變量z的線性模型: $z = x \, c_1 + y \, c_2 + i + e$ 這個模型可以被視為在3D世界中用一個平面去擬合 (x, y, z) 的點云。 ![](http://www.scipy-lectures.org/_images/plot_regression_3d_1.png) **實例: 鳶尾花數據 ([examples/iris.csv](examples/iris.csv))** 萼片和花瓣的大小似乎是相關的: 越大的花越大! 但是，在不同的種之間是否有額外的系統效應? ![](http://www.scipy-lectures.org/_images/plot_iris_analysis_1.png) In?[33]: ``` data = pandas.read_csv('examples/iris.csv') model = ols('sepal_width ~ name + petal_length', data).fit() print(model.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: sepal_width R-squared: 0.478 Model: OLS Adj. R-squared: 0.468 Method: Least Squares F-statistic: 44.63 Date: Thu, 19 Nov 2015 Prob (F-statistic): 1.58e-20 Time: 09:56:04 Log-Likelihood: -38.185 No. Observations: 150 AIC: 84.37 Df Residuals: 146 BIC: 96.41 Df Model: 3 Covariance Type: nonrobust ====================================================================================== coef std err t P>|t| [95.0% Conf. Int.] -------------------------------------------------------------------------------------- Intercept 2.9813 0.099 29.989 0.000 2.785 3.178 name[T.versicolor] -1.4821 0.181 -8.190 0.000 -1.840 -1.124 name[T.virginica] -1.6635 0.256 -6.502 0.000 -2.169 -1.158 petal_length 0.2983 0.061 4.920 0.000 0.178 0.418 ============================================================================== Omnibus: 2.868 Durbin-Watson: 1.753 Prob(Omnibus): 0.238 Jarque-Bera (JB): 2.885 Skew: -0.082 Prob(JB): 0.236 Kurtosis: 3.659 Cond. No. 54.0 ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` ### 3.1.3.3 事后假設檢驗: 方差分析 (ANOVA)) 在上面的鳶尾花例子中，在排除了萼片的影響之后，我們想要檢驗versicolor和virginica的花瓣長度是否有差異。這可以被公式化為檢驗在上面的線性模型中versicolor和virginica系數的差異 (方差分析, ANOVA)。我們寫了"差異"向量的參數來估計: 我們想要用[F-檢驗](https://en.wikipedia.org/wiki/F-test)檢驗 "`name[T.versicolor] - name[T.virginica]`": In?[36]: ``` print(model.f_test([0, 1, -1, 0])) ``` ``` <F test: F=array([[ 3.24533535]]), p=0.073690587817, df_denom=146, df_num=1> ``` 是否差異顯著？ > **練習** 回到大腦大小 + IQ 數據, 排除了大腦大小、高度和重量的影響后，檢驗男女的VIQ差異。 ## 3.1.4 更多可視化: 用seaborn來進行統計學探索 [Seaborn](http://stanford.edu/~mwaskom/software/seaborn/) 集成了簡單的統計學擬合與pandas dataframes繪圖。讓我們考慮一個500個個體的工資及其它個人信息的數據 ([Berndt, ER. The Practice of Econometrics. 1991\. NY: Addison-Wesley](http://lib.stat.cmu.edu/datasets/CPS_85_Wages))。加載并繪制工資數據的完整代碼可以在[對應的例子](http://www.scipy-lectures.org/packages/statistics/auto_examples/plot_wage_data.html#example-plot-wage-data-py)中找到。 In?[3]: ``` print data ``` ``` EDUCATION SOUTH SEX EXPERIENCE UNION WAGE AGE RACE OCCUPATION \ 0 8 0 1 21 0 5.10 35 2 6 1 9 0 1 42 0 4.95 57 3 6 2 12 0 0 1 0 6.67 19 3 6 3 12 0 0 4 0 4.00 22 3 6 4 12 0 0 17 0 7.50 35 3 6 5 13 0 0 9 1 13.07 28 3 6 6 10 1 0 27 0 4.45 43 3 6 7 12 0 0 9 0 19.47 27 3 6 8 16 0 0 11 0 13.28 33 3 6 9 12 0 0 9 0 8.75 27 3 6 10 12 0 0 17 1 11.35 35 3 6 11 12 0 0 19 1 11.50 37 3 6 12 8 1 0 27 0 6.50 41 3 6 13 9 1 0 30 1 6.25 45 3 6 14 9 1 0 29 0 19.98 44 3 6 15 12 0 0 37 0 7.30 55 3 6 16 7 1 0 44 0 8.00 57 3 6 17 12 0 0 26 1 22.20 44 3 6 18 11 0 0 16 0 3.65 33 3 6 19 12 0 0 33 0 20.55 51 3 6 20 12 0 1 16 1 5.71 34 3 6 21 7 0 0 42 1 7.00 55 1 6 22 12 0 0 9 0 3.75 27 3 6 23 11 1 0 14 0 4.50 31 1 6 24 12 0 0 23 0 9.56 41 3 6 25 6 1 0 45 0 5.75 57 3 6 26 12 0 0 8 0 9.36 26 3 6 27 10 0 0 30 0 6.50 46 3 6 28 12 0 1 8 0 3.35 26 3 6 29 12 0 0 8 0 4.75 26 3 6 .. ... ... ... ... ... ... ... ... ... 504 17 0 1 10 0 11.25 33 3 5 505 16 0 1 10 1 6.67 32 3 5 506 16 0 1 17 0 8.00 39 2 5 507 18 0 0 7 0 18.16 31 3 5 508 16 0 1 14 0 12.00 36 3 5 509 16 0 1 22 1 8.89 44 3 5 510 17 0 1 14 0 9.50 37 3 5 511 16 0 0 11 0 13.65 33 3 5 512 18 0 0 23 1 12.00 47 3 5 513 12 0 0 39 1 15.00 57 3 5 514 16 0 0 15 0 12.67 37 3 5 515 14 0 1 15 0 7.38 35 2 5 516 16 0 0 10 0 15.56 32 3 5 517 12 1 1 25 0 7.45 43 3 5 518 14 0 1 12 0 6.25 32 3 5 519 16 1 1 7 0 6.25 29 2 5 520 17 0 0 7 1 9.37 30 3 5 521 16 0 0 17 0 22.50 39 3 5 522 16 0 0 10 1 7.50 32 3 5 523 17 1 0 2 0 7.00 25 3 5 524 9 1 1 34 1 5.75 49 1 5 525 15 0 1 11 0 7.67 32 3 5 526 15 0 0 10 0 12.50 31 3 5 527 12 1 0 12 0 16.00 30 3 5 528 16 0 1 6 1 11.79 28 3 5 529 18 0 0 5 0 11.36 29 3 5 530 12 0 1 33 0 6.10 51 1 5 531 17 0 1 25 1 23.25 48 1 5 532 12 1 0 13 1 19.88 31 3 5 533 16 0 0 33 0 15.38 55 3 5 SECTOR MARR 0 1 1 1 1 1 2 1 0 3 0 0 4 0 1 5 0 0 6 0 0 7 0 0 8 1 1 9 0 0 10 0 1 11 1 0 12 0 1 13 0 0 14 0 1 15 2 1 16 0 1 17 1 1 18 0 0 19 0 1 20 1 1 21 1 1 22 0 0 23 0 1 24 0 1 25 1 1 26 1 1 27 0 1 28 1 1 29 0 1 .. ... ... 504 0 0 505 0 0 506 0 1 507 0 1 508 0 1 509 0 1 510 0 1 511 0 1 512 0 1 513 0 1 514 0 1 515 0 0 516 0 0 517 0 0 518 0 1 519 0 1 520 0 1 521 1 1 522 0 1 523 0 1 524 0 1 525 0 1 526 0 0 527 0 1 528 0 0 529 0 0 530 0 1 531 0 1 532 0 1 533 1 1 [534 rows x 11 columns] ``` ### 3.1.4.1 配對圖: 散點矩陣使用[seaborn.pairplot()](http://stanford.edu/~mwaskom/software/seaborn/generated/seaborn.pairplot.html#seaborn.pairplot)來顯示散點矩陣我們可以很輕松的對連續變量之間的交互有一個直覺: In?[4]: ``` import seaborn seaborn.pairplot(data, vars=['WAGE', 'AGE', 'EDUCATION'], kind='reg') ``` Out[4]: ``` <seaborn.axisgrid.PairGrid at 0x107feb850> ``` ``` /Library/Frameworks/Python.framework/Versions/2.7/lib/python2.7/site-packages/matplotlib/collections.py:590: FutureWarning: elementwise comparison failed; returning scalar instead, but in the future will perform elementwise comparison if self._edgecolors == str('face'): ``` ![](https://box.kancloud.cn/2016-03-21_56efdc0bd2d74.png) 可以用顏色來繪制類別變量: In?[5]: ``` seaborn.pairplot(data, vars=['WAGE', 'AGE', 'EDUCATION'], kind='reg', hue='SEX') ``` Out[5]: ``` <seaborn.axisgrid.PairGrid at 0x107feb650> ``` ![](https://box.kancloud.cn/2016-03-21_56efdc0bef52d.png) **看一下并感受一些matplotlib設置** Seaborn改變了matplotlib的默認圖案以便獲得更"現代"、更"類似Excel"的外觀。它是通過import來實現的。重置默認設置可以使用: In?[8]: ``` from matplotlib import pyplot as plt plt.rcdefaults() ``` 要切換回seaborn設置, 或者更好理解seaborn中的樣式, 見[seaborn文檔中的相關部分](http://stanford.edu/~mwaskom/software/seaborn/tutorial/aesthetics.html)。 ### 3.1.4.2\. lmplot: 繪制一個單變量回歸回歸捕捉了一個變量與另一個變量的關系，例如薪水和教育，可以用[seaborn.lmplot()](http://stanford.edu/~mwaskom/software/seaborn/generated/seaborn.lmplot.html#seaborn.lmplot)來繪制: In?[6]: ``` seaborn.lmplot(y='WAGE', x='EDUCATION', data=data) ``` Out[6]: ``` <seaborn.axisgrid.FacetGrid at 0x108db6050> ``` ![](https://box.kancloud.cn/2016-03-21_56efdc0c148ab.png) **穩健回歸** 在上圖中，有一些數據點偏離了右側的主要云，他們可能是異常值，對總體沒有代表性，但是，推動了回歸。要計算對異常值不敏感的回歸，必須使用[穩健模型](https://en.wikipedia.org/wiki/Robust_statistics)。在seaborn的繪圖函數中可以使用`robust=True`，或者在statsmodels用"穩健線性回歸"`statsmodels.formula.api.rlm()`來替換OLS。 ## 3.1.5 交互作用檢驗 ![](http://www.scipy-lectures.org/_images/plot_wage_education_gender_1.png) 是否教育對工資的提升在男性中比女性中更多? 上圖來自兩個不同的擬合。我們需要公式化一個簡單的模型來檢驗總體傾斜的差異。這通過"交互作用"來完成。 In?[22]: ``` result = ols(formula='WAGE ~ EDUCATION + C(SEX) + EDUCATION * C(SEX)', data=data).fit() print(result.summary()) ``` ``` OLS Regression Results ============================================================================== Dep. Variable: WAGE R-squared: 0.190 Model: OLS Adj. R-squared: 0.186 Method: Least Squares F-statistic: 41.50 Date: Thu, 19 Nov 2015 Prob (F-statistic): 4.24e-24 Time: 12:06:38 Log-Likelihood: -1575.0 No. Observations: 534 AIC: 3158. Df Residuals: 530 BIC: 3175. Df Model: 3 Covariance Type: nonrobust ========================================================================================= coef std err t P>|t| [95.0% Conf. Int.] ----------------------------------------------------------------------------------------- Intercept 1.1046 1.314 0.841 0.401 -1.476 3.685 C(SEX)[T.1] -4.3704 2.085 -2.096 0.037 -8.466 -0.274 EDUCATION 0.6831 0.099 6.918 0.000 0.489 0.877 EDUCATION:C(SEX)[T.1] 0.1725 0.157 1.098 0.273 -0.136 0.481 ============================================================================== Omnibus: 208.151 Durbin-Watson: 1.863 Prob(Omnibus): 0.000 Jarque-Bera (JB): 1278.081 Skew: 1.587 Prob(JB): 2.94e-278 Kurtosis: 9.883 Cond. No. 170. ============================================================================== Warnings: [1] Standard Errors assume that the covariance matrix of the errors is correctly specified. ``` 我們可以得出結論教育對男性的益處大于女性嗎？ **帶回家的信息** * 假設檢驗和p-值告訴你影響 / 差異的**顯著性** * **公式** (帶有類別變量) 讓你可以表達你數據中的豐富聯系 * **可視化**數據和簡單模型擬合很重要! * **條件化** (添加可以解釋所有或部分方差的因素) 在改變交互作用建模方面非常重要。 ## 3.1.6 完整例子 ### [3.1.6.1 例子](http://www.scipy-lectures.org/packages/statistics/auto_examples/index.html) #### [3.1.6.1.1 代碼例子](http://www.scipy-lectures.org/packages/statistics/auto_examples/index.html#code-examples) #### [3.1.6.1.2 課程練習的答案](http://www.scipy-lectures.org/packages/statistics/auto_examples/index.html#solutions-to-the-exercises-of-the-course)