[TOC] ## 1. 什么是聚類 * **機器學習的分類：** * **監督式學習**：訓練集有明確答案，監督學習就是尋找問題（又稱輸入、特征、自變量）與答案（又稱輸出、目標、因變量）之間關系的學習方式。監督學習模型有兩類，分類和回歸。 * ? 分類模型：目標變量是離散的分類型變量； * ? 回歸模型：目標變量是連續性數值型變量。 * **無監督學習**：只有數據，無明確答案，即訓練集沒有標簽。常見的無監督學習算法有聚類(clustering)，由計算機自己找出規律，把有相似屬性的樣本放在一組，每個組也稱為簇（cluster）。 * 最早的聚類分析是在考古分類、昆蟲分類研究中發展起來的，目的是找到隱藏于數據中客觀存在的“自然小類”，“自然小類”具有類內結構相似、類間結構差異顯著的特點，**通過刻畫“自然小類”可以發現數據中的規律、揭示數據的內在結構**。 * 之前一起學了**回歸算法**中超級典型的線性回歸，**分類算法**中非常難懂的SVM，這兩都是**有監督學習**中的模型，那今天就來看看**無監督學習**中最最基礎的**聚類算法**——K-Means Cluster吧。 ## 2. K-Means步驟 * K-Means聚類步驟是一個循環迭代的算法，非常簡單易懂： * 1. 假定我們要對N個樣本觀測做聚類，要求聚為K類，首先選擇K個點作為**初始中心點**； * 2. 接下來，按照**距離初始中心點最小**的原則，把所有觀測分到各中心點所在的類中； * 3. 每類中有若干個觀測，計算K個類中**所有樣本點的均值**，作為第二次迭代的K個中心點； * 4. 然后根據這個中心重復第2、3步，直到**收斂（中心點不再改變或達到指定的迭代次數）**，聚類過程結束。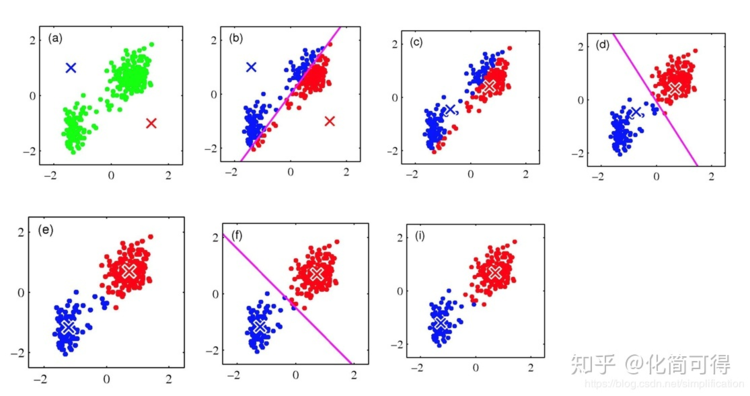 * 以二維平面中的點![[公式]](https://www.zhihu.com/equation?tex=X_%7Bi%7D%3D%28x_%7Bi1%7D%2Cx_%7Bi2%7D%29%2Ci%3D1%2C...%2Cn)為例，用圖片展示K=2時的迭代過程： :-:  * 1. 現在我們要將(a)圖中的n個綠色點聚為2類，先隨機選擇藍叉和紅叉分別作為初始中心點； * 2. 分別計算所有點到初始藍叉和初始紅叉的距離，![[公式]](https://www.zhihu.com/equation?tex=X_%7Bi%7D%3D%28x_%7Bi1%7D%2Cx_%7Bi2%7D%29)距離藍叉更近就涂為藍色，距離紅叉更近就涂為紅色，遍歷所有點，直到全部都染色完成，如圖(b)； * 3. 現在我們不管初始藍叉和初始紅叉了，對于已染色的紅色點計算其紅色中心，藍色點亦然，得到第二次迭代的中心，如圖(c)； * 4. 重復第2、3步，直到收斂，聚類過程結束。 * 看完K-Means算法步驟的文字描述，我們可能會有以下疑問： * 1. 第一步中的**初始中心點怎么確定**？隨便選嗎？不同的初始點得到的最終聚類結果也不同嗎？ * 2. 第二步中**點之間的距離**用什么來定義？ * 3. 第三步中的**所有點的均值**（新的中心點）怎么算？ * 4. **K怎么選擇**？ ## 3. K-Means的數學描述 * 我們先解答第2個和第3個問題，其他兩個問題放到后面小節中再說。 * * 聚類是把相似的物體聚在一起，這個相似度（或稱距離）是用什么來度量的呢？——**歐氏距離**。 * * 給定兩個樣本![[公式]](https://www.zhihu.com/equation?tex=X%3D%28x_%7B1%7D%2Cx_%7B2%7D%2C...%2Cx_%7Bn%7D%29)與![[公式]](https://www.zhihu.com/equation?tex=Y%3D%28y_%7B1%7D%2Cy_%7B2%7D%2C...%2Cy_%7Bn%7D%29)，其中n表示特征數 ，X和Y兩個向量間的歐氏距離(Euclidean Distance)表示為： * :-: ![[公式]](https://www.zhihu.com/equation?tex=dist_%7Bed%7D%28X%2CY%29%3D%7C%7CX-Y%7C%7C%7B2%7D%3D%5Csqrt%5B2%5D%7B%28x%7B1%7D-y_%7B1%7D%29%5E%7B2%7D%2B...%2B%28x_%7Bn%7D-y_%7Bn%7D%29%5E%7B2%7D%7D) * * k-means算法是把數據給分成不同的簇，目標是同一個簇中的差異小，不同簇之間的差異大，這個目標怎么用數學語言描述呢？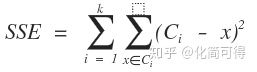我們一般用**誤差平方和**作為目標函數（想想線性回歸中說過的殘差平方和、損失函數，是不是很相似），公式如下: * :-:  * 其中C表示聚類中心，如果x屬于Ci這個簇，則計算兩者的歐式距離，將所有樣本點到其中心點距離算出來，并加總，就是k-means的目標函數。實現同一個簇中的樣本差異小，就是最小化SSE。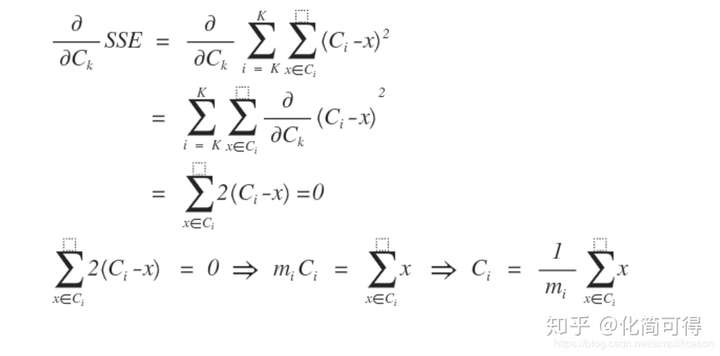 * * 我們知道，可以通過求導來求函數的極值，我們對SSE求偏導看看能得到什么結果： * * :-:  * 式中m是簇中點的數量，發現了沒有，這個C的解，就是X的均值點。多點的均值點應該很好理解吧，給定一組點![[公式]](https://www.zhihu.com/equation?tex=X_%7B1%7D%2C...%2CX_%7Bm%7D)，其中![[公式]](https://www.zhihu.com/equation?tex=X_%7Bi%7D%3D%28x_%7Bi1%7D%2Cx_%7Bi2%7D%2C...%2Cx_%7Bin%7D%29)，這組點的均值向量表示為： * * ![[公式]](https://www.zhihu.com/equation?tex=++++C%3D%28%5Cfrac%7Bx_%7B11%7D%2B...%2Bx_%7B1n%7D%7D%7Bm%7D%2C...%2C%5Cfrac%7Bx_%7Bm1%7D%2B...%2Bx_%7Bmn%7D%7D%7Bm%7D%29%3D%5Cfrac%7B%5Csum+x%7D%7Bm%7D) ## 4. 初始中心點怎么確定 * 在k-means算法步驟中，有兩個地方降低了SSE： * * 1. 把樣本點分到最近鄰的簇中，這樣會降低SSE的值； * 2. 重新優化聚類中心點，進一步的減小了SSE。 * * 這樣的重復迭代、不斷優化，會找到**局部最優解（局部最小的SSE）**，如果想要找到全局最優解需要找到合理的初始聚類中心。 * * 那合理的初始中心怎么選？ * * 方法有很多，譬如先隨便選個點作為第1個初始中心C1，接下來計算所有樣本點與C1的距離，距離最大的被選為下一個中心C2，直到選完K個中心。這個算法叫做**K-Means++**，可以理解為 K-Means的改進版，它可以能有效地解決初始中心的選取問題，但**無法解決離群點問題**。 * * 我自己也想了一個方法，先找所有樣本點的均值點，計算每個點與均值點的距離，選取最遠的K個點作為K個初始中心。當然，如果樣本中有離群點，這個方法也不佳。 * * 總的來說，最好解決辦法還是多嘗試幾次，即**多設置幾個不同的初始點**，從中選最優，也就是具有最小SSE值的那組作為最終聚類。 ## 5. K值怎么確定 * 要知道，**K設置得越大，樣本劃分得就越細，每個簇的聚合程度就越高，誤差平方和SSE自然就越小**。所以不能單純像選擇初始點那樣，用不同的K來做嘗試，選擇SSE最小的聚類結果對應的K值，因為這樣選出來的肯定是你嘗試的那些K值中最大的那個。 * * 確定K值的一個主流方法叫“**手肘法**”。 * * 如果我們拿到的樣本，客觀存在J個“自然小類”，這些真實存在的小類是隱藏于數據中的。三維以下的數據我們還能畫圖肉眼分辨一下J的大概數目，更高維的就不能直觀地看到了，我們只能從一個比較小的K，譬如K=2開始嘗試，去逼近這個真實值J。 * * * 當K小于樣本真實簇數J時，K每增大一個單位，就會大幅增加每個簇的聚合程度，這時SSE的下降幅度會很大； * * 當K接近J時，再增加K所得到的聚合程度回報會迅速變小，SSE的下降幅度也會減小； * * 隨著K的繼續增大，SSE的變化會趨于平緩。 * * 例如下圖，真實的J我們事先不知道，那么從K=2開始嘗試，發現K=3時，SSE大幅下降，K=4時，SSE下降幅度稍微小了點，K=5時，下降幅度急速縮水，再后面就越來越平緩。所以我們認為J應該為4，因此可以將K設定為4。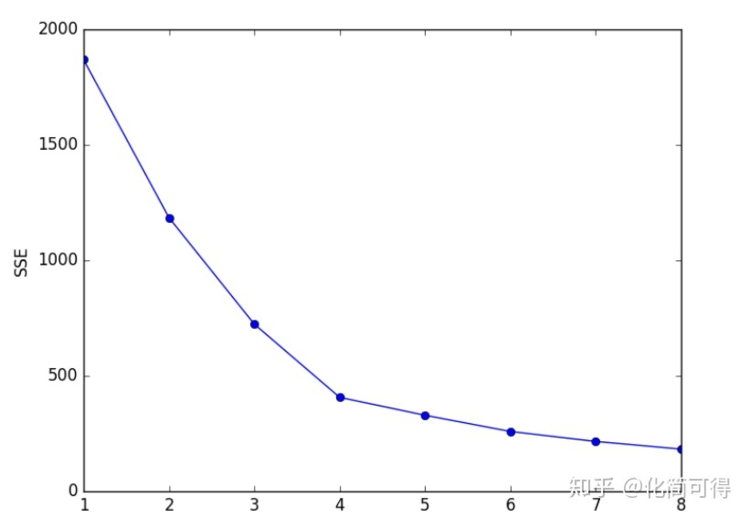 * :-:  * 叫“手肘法”可以說很形象了，因為SSE和K的關系圖就像是手肘的形狀，而**肘部對應的K值就被認為是數據的真實聚類數**。 * * 當然還有其他設定K值的方法，這里不贅述，總的來說還是要結合自身經驗多做嘗試，要知道沒有一個方法是完美的。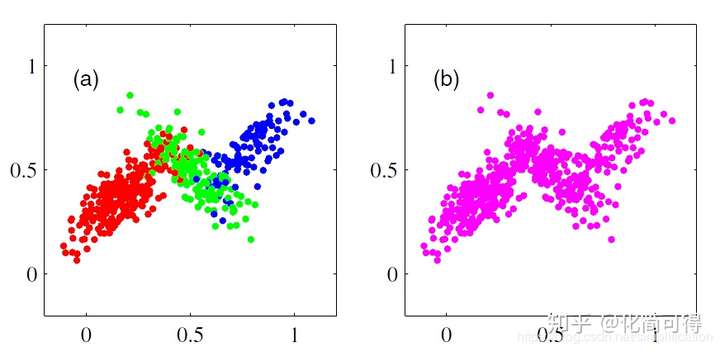 * * 而且，聚類有時是比較主觀的事，比如下面這組點，真實簇數J是幾呢？我們既可以說J=3，也可以就把它分成2個簇。 * *  ## 6. 小結 * K-Means優點在于原理簡單，容易實現，聚類效果好。 * * 當然，也有一些缺點： * * 1. K值、初始點的選取不好確定； * 2. 得到的結果只是局部最優； * 3. 受離群值影響大。