[TOC] ## **1. 簡介** * **協同過濾（Collaborative filtering，CF）** 與基于內容的推薦算法一樣，也是一個非常古老的推薦算法。但是直至今日，協同過濾依然是應用最廣泛的推薦算法，在推薦領域占有極其重要的地位，甚至 “協同過濾” 一度成為推薦系統的代名詞。按維基百科的說法，協同過濾有廣義和狹義兩種定義，廣義協同過濾是指采用某項技術，對多源數據（如不同的代理、視點、數據源等）之間的協作（共同點）進行過濾處理的過程；而狹義的協同過濾則是一種通過收集眾多偏好口味相似的用戶信息（協同）來對某一用戶的興趣進行自動預測（過濾）的方法。廣義定義從狹義定義中人的協同上升到了信息媒介的協同，在推薦算法中，我們談到的協同過濾更多是指狹義定義的協同過濾。 ## **2. 協同過濾的分類** * 在聊協同過濾的基本思想之前，我們先談談協同過濾的分類。 * 協同過濾的定義其實非常寬泛，凡是借助于群體信息來進行信息過濾的推薦算法都可歸為協同過濾，而實際上根據算法本身內部機制的不同，協同過濾算法又可以分為不同的幾種類別。但凡分類，大都有個角度作為基準線，“橫看成嶺側成峰”，角度不同，分得的類別也就不同。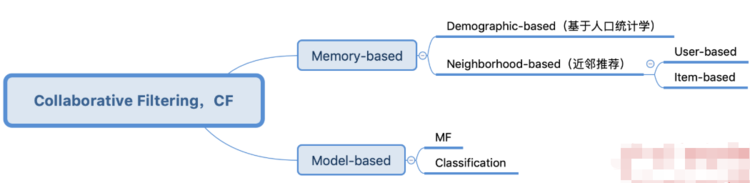協同過濾在業界也有不同的分類方法，我這里說一個范圍稍大一點的分類體系，具體可參考下圖： *  * 由上可知，協同過濾可以分為**基于記憶（Memory-based）** 和 **基于模式（Model-based）** 兩大類，其中基于記憶的協同過濾又可分為**基于人口統計學（Demographic-based）** 和 **基于近鄰（Neighborhood-based）** 兩個子類，基于近鄰又可分為**基于用戶（User-based）** 和 **基于物品（Item-based）** 兩個小類。 * 所謂基于記憶，就是通過歷史行為數據來找到某種人（User）和物（Item）的可能關聯來進行推薦，如果利用眾多人口統計學信息進行人與物的關聯計算，那便是基于人口統計學的協同過濾，可能會得到一個較粗的推薦結論，比如某個城市某個年齡段的女性在某個季節喜歡買什么東西；還有就是用近鄰關系去衡量這種可能關聯，用人與人之間的近鄰（相似性）就是基于用戶，用物與物的之間近鄰（相似性）就是基于物品。 * 基于模型的協同過濾又可分為**基于矩陣分解（Matrix Factorization, MF）** 和 基于**分類模型（Classification Model）** 的協同過濾，本文主要講解基于近鄰的協同過濾。 ## **3. 基本思路** * 我們通過先從三個關鍵詞來理解協同過濾的基本思路，即集體智慧、共現關系和近鄰推薦。 * **集體智慧**：協同過濾是一種集體智慧的體現，也就是需要借助于群體信息。從另一個角度來講，其實就是 “借用數據”，在自身數據稀缺的情況下利用其他相似的信息幫助建模； * **共現關系**：協同過濾中的 “群體” 是基于物品的共現關系來構建的，比如兩個物品同時在很多用戶身上的共現，或很多用戶在對物品行為上的共現; * **近鄰推薦**：協同過濾是基于相似信息的推薦模型，即根據用戶在物品上的行為找到物品或者用戶的 “近鄰”，這里的 “鄰”，一般指群體，其基本假設是相似的用戶可能會有相似的喜好，相似的物品可能會被相似的人所偏好。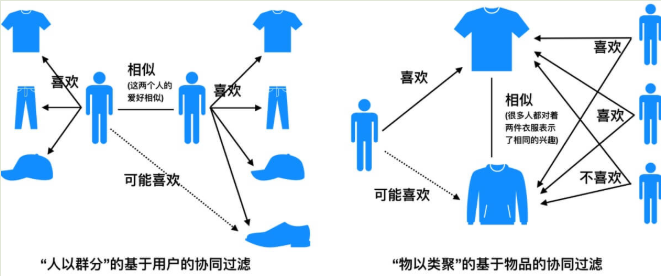 *  * 然后我們把基于內容的推薦算法也拉進來，*來看看基于內容、基于用戶的協同、基于物品的協同算法召回的核心思想和不同之處，所謂核心思想其實也是一種合理化推薦的假設設定。* * **基于內容的推薦算法：給用戶推薦和他之前喜歡的物品相似的物品。** * **基于用戶的協同過濾算法：給用戶推薦和他興趣相似的其他用戶喜歡的物品。** * **基于物品的協同過濾算法：給用戶推薦和他之前喜歡的物品相似（相關）的物品。** * 推薦算法目的是幫用戶找到潛在的可能喜歡的物品，只是這三種算法對這種可能性的前提假設不同，也導致對物品喜歡可能性量化的衡量標準也不一樣。 * 如果你很細心，會發現基于內容的推薦算法和基于物品的協同過濾算法的思想在文字表述上基本一致，但其實它們背后的假設和衡量標準完全不同，為了以示區別，我特別在相似的后面注明了 “相關” 二字。接下來我將詳細闡述三種合理化推薦假設的背后的不同之處。 ### **基于內容的推薦算法：** * 基于內容的推薦算法的關鍵點在內容上，你購買過一件商品后，這種算法會尋找和這個物品內容上接近的物品，因為內容大都提取自物品的相關特征或者相關描述，因此這種方式推薦的物品其實都是和你所購商品在某方面十分相似的，這也決定了基于內容的推薦算法沒有太大的驚喜度。當然，如果歷史購買物品很多的話，有些算法會把這種相似對比的基準從一個物品轉化到用戶的整體偏好上，用粗一點的粒度給用戶推薦，驚喜度要比一件商品更好一點，但其本質思想都是基于內容的相似。 ### **基于物品的協同過濾算法：** * 基于物品的協同過濾算法雖然也是找和用戶之前喜歡的物品相似的物品，但這里的 “相似” 其實用 “相關” 更合適，因為基于物品的協同過濾是基于共現關系來衡量物品的相似性的，也就是通過用戶群體行為來衡量兩個物品是否有關聯，而不是某兩件商品是否在某些特點上相似。當你購買了一件物品后，基于物品的協同過濾算法會幫你找出有哪些商品與你購買的商品一同出現在了其他用戶的歷史購物清單上，當你購買的物品和候選物品共現得越多，即同時購買過這兩件商品的用戶數越多，就證明這兩件商品的相關性越大，該物品則被你需要的可能性也越大。一個典型的例子就是 “啤酒與尿布” 的故事，從 “內容” 上看，這二者實在沒有任何相似性，但是它們被大量的人同時購買過，共現次數非常多，也就說明這兩件商品的相關性非常大，所以如果你買了尿布還沒買啤酒，給你推薦啤酒就是非常合理的。其實推薦算法中的相似是一個非常籠統的概念，即便上述的相關性、共現關系也都可以說成相似，而且如果是評分預估的話更是會用[相似度](https://lumingdong.cn/tag/%e7%9b%b8%e4%bc%bc%e5%ba%a6 "View all posts in 相似度")度量，這也是為什么很多書籍資料對基于物品的協同過濾算法進行描述時也會用 “相似” 二字。而且通過以上思想你應該也能理解，為什么基于物品的協同過濾算法，對某個用戶僅需要計算每個已購物品與候選物品的相關性即可，而不需要對所有物品都要計算。 ### **基于用戶的協同過濾算法：** * 基于用戶的協同過濾算法其實很好理解，先找到與待推薦用戶興趣相似的用戶群體，然后把那些用戶喜歡的而待推薦用戶沒有發生行為的物品推薦給它，這種方式其實也是一個給用戶聚類的過程，把用戶按照興趣口味聚類成不同的群體，給用戶產生的推薦就來自這個群體的平均值。用戶興趣[相似度](https://lumingdong.cn/tag/%e7%9b%b8%e4%bc%bc%e5%ba%a6 "View all posts in 相似度")量其實也可以說是一種共現關系的度量，兩個用戶歷史購物清單中購買的相同物品越多，那么這兩個用戶的興趣也就越相似。 * *其實之后演化的大多數算法包括應用了深度學習模型的推薦算法，其核心思想和推薦假設應該都是基于上面這三條的，只不過它們在計算方式上以及流程細節上更加更完善了。* ## **4. 架構流程** * 基于鄰域的協同過濾主要有**基于用戶的協同過濾（User-Based，UserCF，User to User，U2U）**和**基于物品的協同過濾（Item-Based，ItemCF， Item to Item，I2I）**兩種，具體流程我們分別來談。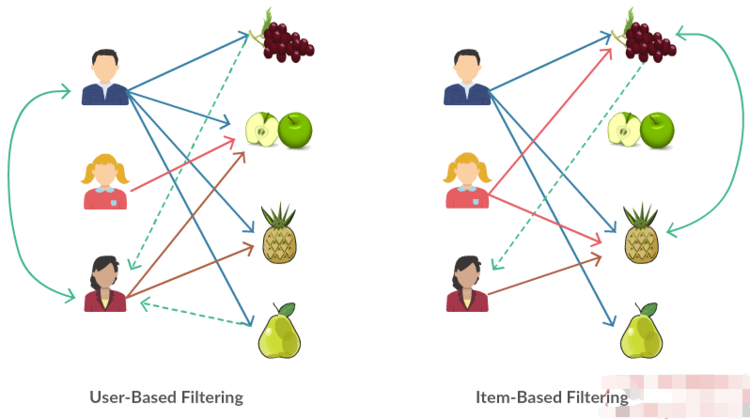 ### **4.1 基本流程** *  * 協同過濾的過程簡單來說只有兩個，計算相似度，然后計算物品得分。 **基于用戶的協同過濾** * 1）找到和目標用戶興趣相似的用戶集合。 * 2）找到這個集合中的用戶喜歡的，且目標用戶沒有聽說過的物品推薦給目標用戶。 **基于物品的協同過濾** * 1）計算物品之間的相似度。 * 2）根據物品的相似度和用戶的歷史行為給用戶生成推薦列表。 ### **4.2 矩陣補全** * 如果對**協同過濾整個過程用數學形式化表達，其實是一個矩陣補全問題**（矩陣也是網絡或圖的一種表達）。這個原始的矩陣是一個用戶和物品的關系矩陣，矩陣的值是用戶對物品的態度，值可以是隱式反饋的布爾值，1 表示有過行為，比如喜歡過、點擊過、購買過，0 表示沒有，這種矩陣稱之為**行為矩陣**；另外矩陣的值也可以是顯示反饋的評分，比如 0 到 5 的取值，這種矩陣稱之為**評分矩陣**。因為用戶不可能對所有的物品都有行為（都有的話也不必推薦了），所以矩陣是稀疏的，并不是每個位置都有，協同過濾的目的就是把那些還沒有的地方填起來。其實基于模型的協同過濾也是從用戶物品關系矩陣中去學習一個模型，從而把那些矩陣空白處填滿。 * 由此可見，這個用戶和物品的關系矩陣是協同過濾的核心，一切都圍繞它來進行。所有的協同過濾算法，一定是基于用戶行為的，和推薦物品本身的內容沒有任何關系，只在乎哪些人在哪些物品上發生了哪些行為。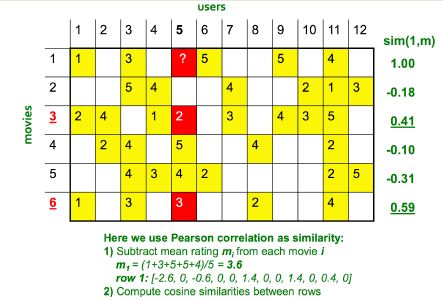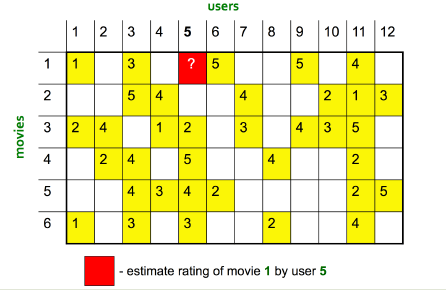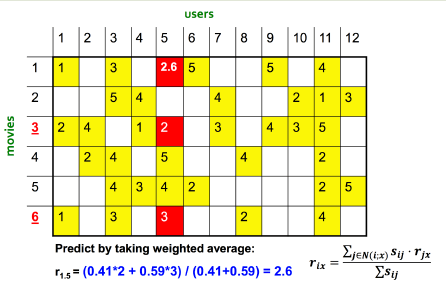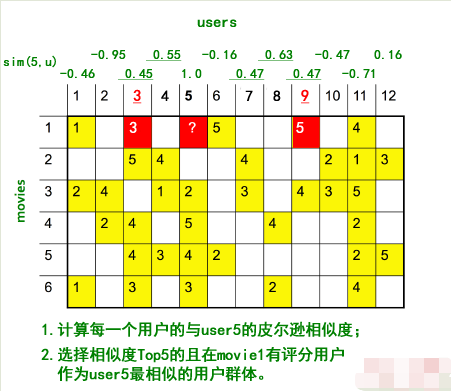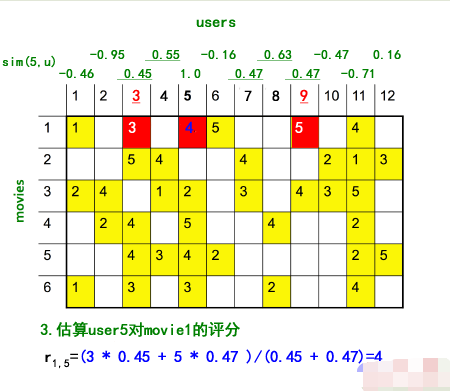 * 矩陣填充示例，預估 user 5 對 movie 1 的評分： *  **使用基于物品的協同過濾：** *  *  **使用基于用戶的協同過濾：** *  *  * 這里特別需要注意幾點 * 1）按照原圖的計算結果，確切地說，這里應該使用的是修正的余弦相似度，而不是皮爾遜相似度（具體區別可參考下一小節），基于用戶的計算過程我為了保持一致性，延用原圖的描述方式。 * 2）ID9 用戶與 ID5 的用戶的皮爾遜相似度很大，甚至超過了 ID3 用戶，但是通過觀察數據便會發現，ID3 似乎與 ID5 更相似才對，而且 ID9 僅有一個評分偏好可以參考，說服力也不強。所以，**如果直接使用相似度作為加權平均的權重，我們可能會過分 “相信” 有一些相關度高但自身數據也不多的用戶，因此在實際應用中，我們可能還需要對相關度進行一個 “重新加權”（Re-Weighting）的過程。具體來說，我們可以把皮爾森相關度乘以一個系數，這個系數是根據自身的偏好數量來定的。**上圖中的例子，僅為了說明過程，因此沒有進行重新加權，關于如何加權提高相似度的置信度，可參考下一小節的內容。 * 3）有時候是先找出有共同評分的用戶然后計算這些用戶的相似度，按具體場景而定。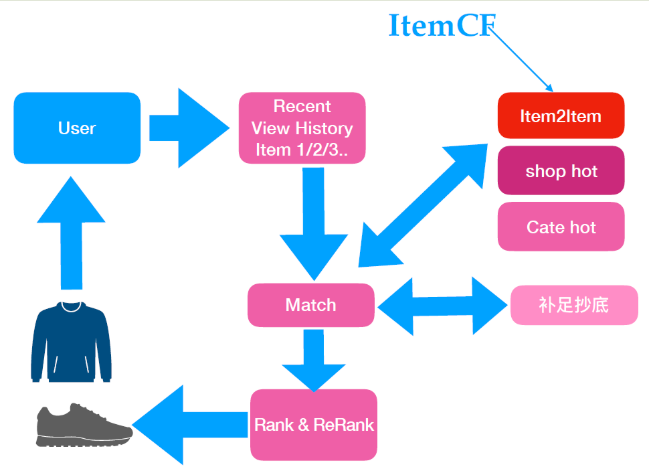 ### **4.3 工業界流程架構** * 下圖是一個簡單的工業界流程架構示例，真實場景中往往比這個更復雜： *  **說明** * 1）上圖中，**補足抄底**是指 Match 階段數據不夠，可能會使用熱門物品進行補足，這個策略主要針對新用戶，行為數據不夠，可用其他算法來彌補； * 2）Rank 通常就是指 Match 后的排序，ReRank 則是在 Rank 階段后的規則把關，根據策略規則進行重排。 ## **5. 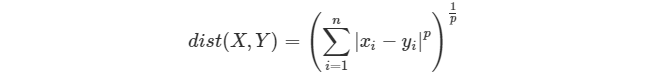相關算法** ### **5.1 相似度計算公式** #### **歐氏距離** * 歐氏距離是閔可夫斯基距離 (Minkowski Distance) 的一個特例，閔可夫斯基距離其實是一組距離的定義，也稱閔氏距離，公式如下： * :-:  * 當 p=1 時為曼哈頓距離，p=2 時為歐氏距離，歐式距離最為常用。關于距離也可參考另一篇文章《[正則化詳細總結 #LP 范數](https://lumingdong.cn/detailed-summary-of-regularization.html#LP%E8%8C%83%E6%95%B0 "正則化詳細總結 #LP范數")》。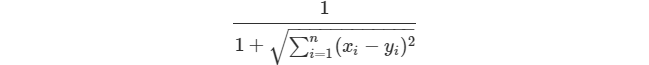 * 有時候會將距離轉為相似度的概念，也就是讓原來距離的 “越小越相似” 改為 “越大越相似”，很簡單，取距離的倒數即可，同時為了避免分母為 0 的情況發生，通常還會在分母上加個 1，于是最后基于距離的相似度公式就變成了： * :-:  * 用距離來作為相似度判定會有一個缺陷，它只能相對地去比較，我們很難去界定相似或者不相似的程度。這個問題可以用皮爾遜相似度來解決，因為它是一個介于-1 和 1 之間的值，通過數值的大小很容易判斷相似程度。 * 歐氏距離 Python 代碼實現： ``` import numpy as np from scipy.spatial import distance def dist(u, v): ## 三種實現方法 ## 1. numpy #return np.sqrt(np.sum(np.square(u - v))) ## 2. np.linalg.norm return np.linalg.norm(u - v) ## 3. 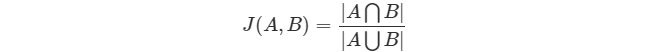scipy # return distance.euclidean(u, v) ``` #### **Jaccard 相似度** * Jaccard 中文名為杰卡德系數、杰卡德相似度，公式為： * :-:  * 其中，|·| 符號表示取長度、數量。上式的含義就是交集的數量除以并集的數量。 * Jaccard 相似度適用于隱式反饋，向量是非連續值，比如集合。 * Jaccard 相似度 Python 代碼實現： ``` import numpy as np from scipy.spatial import distance def jaccard(u, v): ## 兩種實現方法 ## 1. numpy return np.count_nonzero(u*v) / np.count_nonzero(u+v) ## 2. 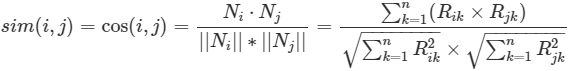scipy # return distance.jaccard(u,v) ``` #### **余弦相似度（Cosine Similarity）** * 余弦相似度的公式： * :-:  * 余弦相似度 Python 代碼實現： ``` import numpy as np from scipy.spatial import distance def cos_sim(u, v): ## 三種實現方法 ## 1. numpy # return np.sum(u * v) / float(np.sqrt(np.sum(u*u)) * np.sqrt(np.sum(v*v))) ## 2. np.linalg.norm return np.dot(u, v) / (np.linalg.norm(u) * np.linalg.norm(v)) ## 3. 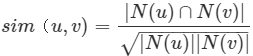scipy（注：distance.cosine()默認計算的是余弦距離，余弦距離=1-余弦相似度，這里換算一下即可） # return 1 - distance.cosine(u, v) ``` * 余弦相似度還有一種比較常見的形式，如下: * :-:  * 在項亮那本書里，這個公式用來計算用戶相似度，其中，N(u)、N(v)表示用戶u、v產生過行為的物品列表，|N(u)|、|N(v)|表示用戶u、v產生過行為的物品數量，|N(u)∩N(v)|表示用戶u、v共同產生行為的物品數量。 * * 這個公式有點類似于 Jaccard 相似度，僅適用于向量是 \[0，1\] 元素的隱式反饋。實際上這個公式就是余弦相似度針對隱式反饋數據的一個簡化，它本身與直接用余弦相似度計算隱式反饋數據的結果是完全一樣的。但在推薦系統中，這個形式的余弦相似度公式也表達出一種特有的意義，那就是體現出隱式反饋協同過濾的共現關系，換句話說，兩個用戶的相似性可以通過二者共同喜歡物品的數量來衡量，二者共同喜歡的物品越多，則他們越相似。這在一定程度上，也符合現實邏輯。因此，我覺得這個公式在某些場景下稱之為 “**共現相似度**” 要更容易理解一些，也可以與余弦相似度原本的公式區分開來。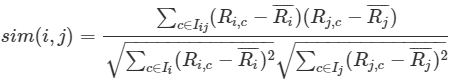 * 共現相似度 Python 代碼實現： ``` import numpy as np def con_sim(u, v): return np.count_nonzero(u*v) / np.sqrt(np.count_nonzero(u)*np.count_nonzero(v)) ``` #### **修正余弦相似度（Adjusted Cosine Similarity）** * 修正余弦相似度，是指中心化（減去平均值）后再求余弦相似度，計算公式如下： * :-:  *  * 修正余弦相似度的 Python 代碼實現： ``` import numpy as np def adjusted_cosine(u, v): # 這里的0代表沒有評分 con_mask = (u != 0) & (v != 0) u_con = u[con_mask] v_con = v[con_mask] numerator = ((u_con - u_con.mean()) * (v_con - v_con.mean())).sum() denominator = (((u - u.mean()) ** 2).sum() * ((v - v.mean()) ** 2).sum()) ** 0.5 return (numerator/denominator, 0)[int(denominator) == 0] ``` #### **皮爾遜相似度（Pearson Correlation Similarity）** * 皮爾遜相似度又常被稱為皮爾遜相關度、皮爾遜相關系數，計算公式如下： * :-:  *  * 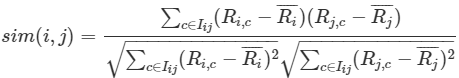這里的提到的皮爾遜相關系數其實與概率論中的提到的皮爾遜相關系數就是同一個東西，對于變量 X 和 Y，上面的皮爾遜系數的表達式其實就是 * :-:  * 皮爾遜相似度與歐式距離相似度的最大區別在于它比歐式距離更重視數據集的整體性；因為皮爾遜相似度計算的是相對距離，歐式距離計算的是絕對距離。就實際應用來說，有不同量綱和單位的數據集適合使用皮爾遜相似度來計算，相同量綱和單位的數據集適合使用歐氏距離。 * 皮爾遜相似度的 Python 代碼實現： ``` import numpy as np from scipy.stats import pearsonr def pearson(u, v): # 這里的0代表沒有評分 con_mask = (u != 0) & (v != 0) u_con = u[con_mask] v_con = v[con_mask] # 1. 使用numpy的相關系數函數 # return np.corrcoef(u_con, v_con)[0][1] # 2. 使用Scipy # return pearsonr(u_con, v_con)[0] # 3. 按公式手寫 numerator = ((u_con - u_con.mean()) * (v_con - v_con.mean())).sum() denominator = (((u_con - u_con.mean()) ** 2).sum() * ((v_con - v_con.mean()) ** 2).sum()) ** 0.5 return (numerator/denominator, 0)[int(denominator) == 0] ``` #### **皮爾遜相似度和修正相似度為什么要去均值？** * 這是因為歐氏距離和余弦相似度都存在著**分數膨脹 (grade inflation)**的問題，比如說 A 和 B 兩個人的評判標準不一樣，A 比較苛刻，給三部電影打的分數是 1、2、1，但是 B 要求不會那么高，給兩部電影打分為 4、5、4，如果用歐氏距離進行相似度度量，會發現他們在二維空間中的距離將會比較大，從而被判為無相似性。但是他們真的是沒有相似性嗎？雖然他們在分數值上存在區別，但是**兩個人在每部電影的評分差上保持一致性，也可認為他們是相似用戶。** 因為在對于好和不好的標準上每個人都會有自己的度量，也許對于 A 來說 2 就算是好的了，但是對于 B 來說好的標準是 5。假如對于多部電影兩者的評分趨勢一致，那么可認為兩者的品味也是差不多的，可以認為他們有相似性。因此，**修正的余弦相似度和皮爾遜相似度都對向量進行了去均值操作，去掉用戶在評分習慣上的差異性，這樣可以使得雙方都處于同一 “標準線”，中心位置都是 0，此時再進行相似度度量就會好很多了。** #### **修正的余弦相似度與皮爾遜之間的區別?** * 修正余弦相似度跟皮爾遜相似度很相似，甚至在很多資料上將二者混為一談，如果只是在數學層面上，不區分共有評分集，向量的元素都參與計算（作為共有評分集），那么計算結果是一致的。但在協同過濾的應用中是有區別的。二者的主要區別在中心化的方式上（分母），**皮爾遜系數的分母采用的評分集是兩個用戶的共同評分集（就是兩個用戶都對這個物品有評價），而修正余弦系數則采用兩個用戶各自的評分集。** * 用直觀的話說，**修正的余弦相似度是先將向量中有評分的地方減去用戶評分均值，然后再去求余弦相似度，而皮爾遜相似度公式中的分母部分只計算用戶共同評分項目偏差和的乘積。** #### **共同評分物品少，相似度不置信如何處理？** * 在上面的例子中我們也提到過，有時候會遇到相似度值高，但是共同評分非常少的情況，這個時候的相似度不置信，我們必須對算好的相似度進行一次 “重新加權”，使得相似度值看上去更加合理。 * 相似度權重可以根據共同評分數量來計算得到，一個比較方便的方法是在原有的相似度基礎上增加一個懲罰因子，當用戶間共同評分項極度稀少時，用懲罰因子適當降低相似度。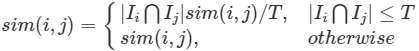改進方法如下公式所示： * :-:  *  * 另一種方式是直接使用 Jaccard 相似度來表示這種用戶評分相似度的置信度，作為重新加權的權重。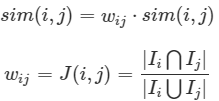 * :-:  * 當用戶共同評價物品數很小時，其評分相似度的置信度也就越小。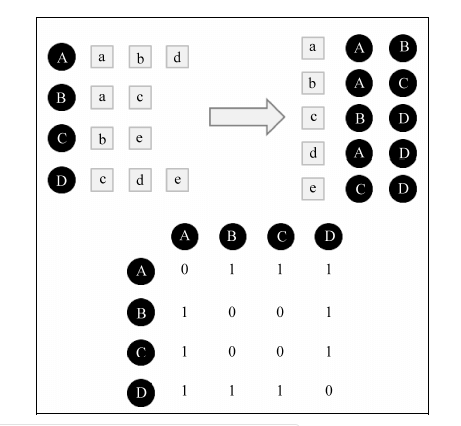 ### **5.2 基于用戶的協同過濾算法** * 1）構建物品倒排索引 *  * 構建物品倒排索引可以加速計算 User-CF 分子。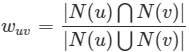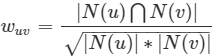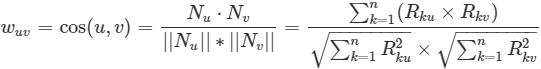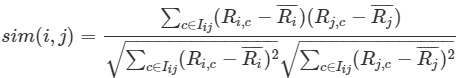 * :-:  * 2）相似度計算 * 建立好物品的倒排索引后，就可以根據相似度公式計算用戶之間的相似度： * * 以下為幾種可用的相似度公式： * * **用戶態度是布爾值類型：** * * Jaccard 相似度： * :-:  *  * 余弦相似度： * :-:  **用戶態度是評分數值類型：** * 余弦相似度 * :-:  * 皮爾遜相似度 * :-:  * 皮爾遜相似度使用更加頻繁一點，它是針對每一個 “兩個用戶” 都同時偏好過的物品，看他們的偏好是否相似，這里的相似是用乘積的形式出現的。當兩個偏好的值都比較大的時候，乘積也就比較大；而只有其中一個比較大的時候，乘積就會比較小。然后，皮爾森相關度對所有的乘積結果進行 “加和” 并且 “歸一化” * * 3）預測評分，生成推薦 * * 有了用戶的相似數據，針對用戶u挑選k個最相似的用戶，把他們購買過的物品中，u未購買過的物品推薦給用戶u即可。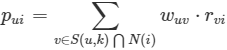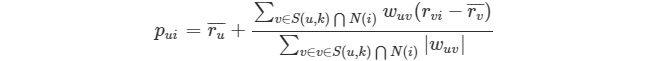如果有評分數據，可以針對這些物品進一步打分，公式如下： * :-:  * 還有一種常見的得分預測方法： * :-:  *  * ### **5.3 基于物品的協同過濾算法** * 基于物品的協同過濾與基于用戶的協同過濾算法過程基本一致。 * * 1）計算物品之間的相似度 * * 傳統物品之間相似度計算同用戶之間的相似度計算完全一樣，只不過將用戶間的相似度換成了物品間的相似度，這里不再贅述。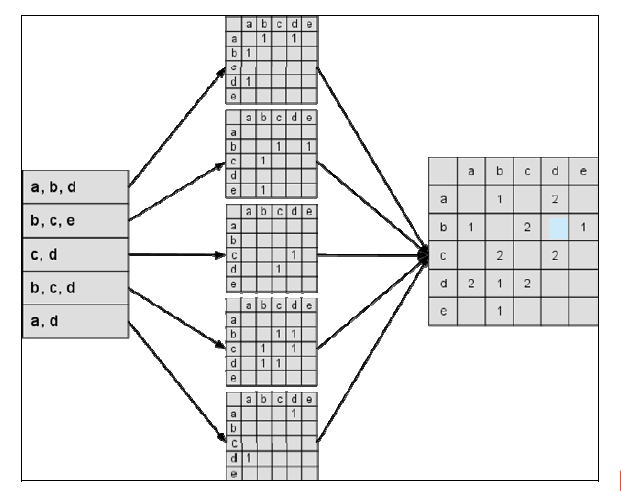 * * 下圖是一種基于隱式反饋得到的物品共現關系矩陣，之后可計算相似度，得到物品的相似度矩陣。 *  * 2）預測評分，生成推薦 * * 預測評分計算和基于用戶的協同過濾算法也是幾乎一樣的。其實就是找到和用戶歷史上感興趣的物品相似的物品，越相似越有可能在用戶的推薦列表中獲得比較高的排名。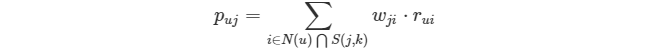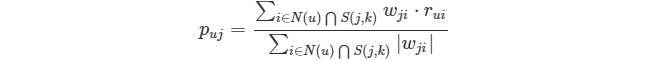 *  * 有時候也用如下公式： *  *  ### **5.4 協同過濾的改進算法和變種** * 在實際應用中，經典的協同過濾算法也會遇到各種各樣的問題，因為協同過濾是一種基于近似關系的算法，所以這種改進很多是體現在對相似度算法上的改進。改進方向包括對熱門物品或用戶的降權，考慮時間因素，提高在線計算的效率等方面。 #### **5.4.1 對熱門用戶和熱門物品進行懲罰降權** * 熱門用戶和物品都會對相似度的計算有很大的影響，會使得與之關聯的相似度都偏高，而且推薦結果過于熱門，也會使個性化的感知降低，因此實際應用中，會在相似度計算時對熱門用戶和熱門物品進行懲罰降權。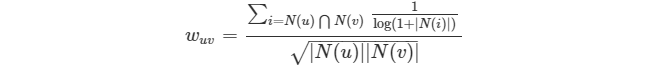 **1）UserCF-IIF：降低熱門物品在計算用戶間相似度的影響** *  *  **2）ItemCF-IUF：降低熱門用戶在計算物品間相似度的影響** *  **3）緩減哈利波特效應，對熱門物品進行懲罰** * 因為《哈利波特》比較熱門，基本購買任何一本書的人似乎都會購買《哈利波特》，這樣會使類似《哈利波特》這樣的熱門物品與很多其他物品之間的相似度都偏高。 * * 比如兩個物品中，物品 j 是非常熱門的物品，按照經典公式： *  * * **熱門物品會與很多物品都有較大的相似度，這樣會導致推薦的覆蓋率和新穎度都不高。** 因此，需要適當的對熱門物品加大懲罰。我們可利用以下改進公式對熱門物品進行懲罰： *  * #### **5.4.2 物品相似度的歸一化** *  * 其實，歸一化的好處不僅僅在于增加推薦的準確度，它還可以提高推薦的覆蓋率和多樣性。一般來說，物品總是屬于很多不同的類，每一類中的物品聯系比較緊密。 #### **5.4.3 綜合業務場景的改進算法** * 在實際應用中，工業界更多的做法是經常會根據自己業務場景中一些問題進行改進和優化，比如下面就是一種改進方法，該方法綜合考慮了用戶行為的時間差（對物品行為反饋的時間差越短，相似度越大，反之越小），以及對熱門用戶的降權。 *  #### **5.4.4 Slope One算法** * Slope One 算法是由 Daniel Lemire 教授在 2005 年提出的一個 Item-Based 的協同過濾推薦算法。 * * 經典的基于物品推薦，相似度矩陣計算無法實時更新，整個過程都是離線計算的，而且還有另一個問題，相似度計算時沒有考慮相似度的置信問題。例如，兩個物品，他們都被同一個用戶喜歡了，且只被這一個用戶喜歡了，那么余弦相似度計算的結果是 1，這個 1 在最后匯總計算推薦分數時，對結果的影響卻最大。 * * Slope One 算法針對這些問題有很好的改進。不過 Slope One 算法專門針對評分矩陣，不適用于行為矩陣。 * * **Slope One 算法是基于不同物品之間的評分差的線性算法，預測用戶對物品評分的個性化算法。** * 過程主要有以下三步： * * Step1：計算物品之間的評分差的均值，記為物品間的評分偏差 (兩物品同時被評分)； *  * Step2：根據物品間的評分偏差和用戶的歷史評分，預測用戶對未評分的物品的評分； *  #### **5.4.5 Swing 算法** * 基于圖結構的實時推薦算法 Swing，能夠計算 item-item 之間的相似性。Swing 指的是秋千，用戶和物品的二部圖中會存在很多這種秋千，例如(u1,u2,i1), 即用戶 1 和 2 都購買過物品i，三者構成一個秋千 (三角形缺一條邊)。這實際上是 3 階交互關系。傳統的啟發式近鄰方法只關注用戶和物品之間的二階交互關系。Swing 會關注這種 3 階關系。這種方法的一個直覺來源于，如果多個 user 在點擊了i1的同時，都只共同點了某一個其他的i2，那么i1和i2一定是強關聯的，這種未知的強關聯關系相當于是通過用戶來傳遞的。另一方面，如果兩個 user pair 對之間構成的 swing 結構越多，則每個結構越弱，在這個 pair 對上每個節點分到的權重越低。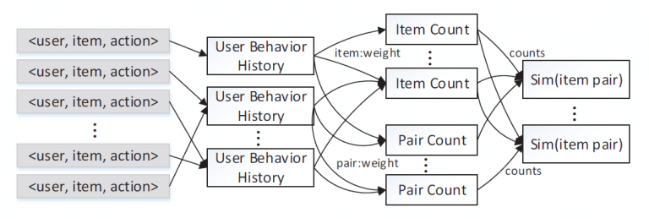公式如下： *  * #### **5.4.6 實時I2I（騰訊2015）** * 下面這種方法是騰訊在 2015 年發表的論文中提到的一種實時增量 Item-CF 算法，可以解決在線場景中新品推薦的問題。這種方法把相關度分數的計算拆分成三個部分，每個部分都可以單獨進行實時增量計算，如下： *  * 這種拆分方法同樣有利于并行計算，如下圖所示的 The Multi-layer Item-based CF： *  #### **5.4.7 多場景下的Hybrid I2I** * I2I 通常解決的是針對給定物品（Trigger item），推薦一系列相關物品 (recommend items) 的問題。因此，I2I 是 feeds 流、瀑布流等推薦場景下的基礎，而 “相似推薦”、“猜你喜歡”、“買了又買” 等場景天然就是 I2I 的問題， 可見 I2I 在推薦系統中的作用至關重要。 * * 但 I2I 在應用實踐中，會衍生出一些其他問題： * * **一個是冷啟動**，常規的 I2I 大都是基于行為的 I2I（Behavior-based I2I），I2I 矩陣計算通常基于物品之間以往的共同行為（例如商品被同一個用戶瀏覽點擊過）, 它在用戶交互行為較為豐富的物品上通常有較好的推薦效果。然而對很多新品較多的場景和應用上，例如上新商品和剛發布的短視頻等，由于沒有歷史行為累計，物品的冷啟動問題異常嚴重，Behavior-based I2I 算法在這些商品上的效果較差。 * 因此，人們考慮在 Behavior-based I2I 的基礎上，引入內容信息，以此來緩解傳統 I2I 的冷啟動問題，這便是 Hybrid I2I，Hybrid I2I 算法通常融合了行為信息和內容信息。 * Hybrid I2I 相關研究工作有很多，較早的做法基本分為兩大類，松耦合（loosely coupled）方法和緊耦合（tightly coupled）方法，松耦合方法就是利用內容信息作為特征來輔助協同過濾（CF）的學習，但是這種方法的弊病是無法通過打分信息來反向指導特征的學習；而緊耦合方法則可以實現雙向交互，所以通常緊耦合方法的效果要優于松耦合方法。不過可惜的是，這些混合方法并不是很好用，尤其是在評分矩陣和物品側信息（side information）非常稀疏的情況下效果非常差。近幾年隨著深度學習的發展，以及嵌入思想在推薦領域的普及，Hybrid I2I 更多地會用 Embedding 來實現，并且也取得了不錯的效果。比如阿里團隊在 2018 年提出的 EGES，在 Graph Embedding 中引入 Side Information，可參考??[推薦系統的中 EMBEDDING 的應用實踐 #EGES](https://lumingdong.cn/application-practice-of-embedding-in-recommendation-system.html#EGES)；以及 2019 年提出利用半參表示算法來進行 Hybird I2I 推薦，可參考??[Hybrid Item-Item Recommendation via Semi-Parametric Embedding](https://lumingdong.cn/go/mk6aph)。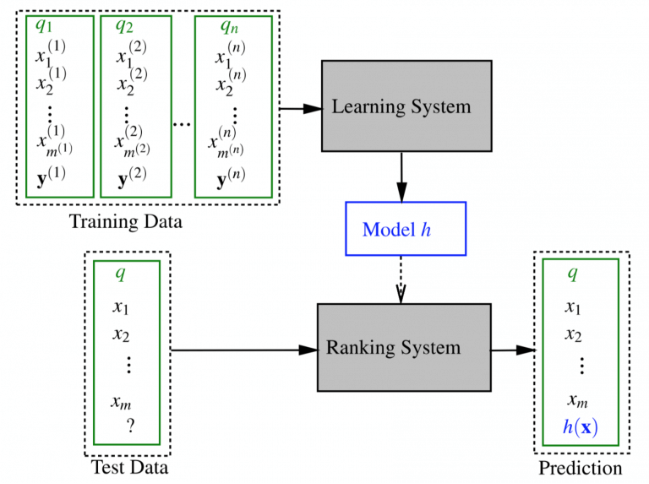 * **另外一個問題則是多場景問題。** 工業界復雜推薦系統通常是多個場景的，比如有相似推薦、猜你喜歡、買了又買等等，但通常為了節省資源，全網數據只能構建一個 I2I 的推薦引擎，那么這個推薦引擎是否在所有場景里都很適合？傳統的 I2I 算法很難兼顧多個場景，這個時候可以用一個[機器學習](http://lumingdong.cn/category/tech/ml "機器學習技術文章")模型來實現多場景下的自動學習。有機器學習模型，自然可以加入很多可用的特征，如物品側屬性特征和歷史交互行為特征。具體而言，其實是構造一個機器學習的分類模型，通過在不同場景下的點擊行為反饋來學習到在各個不同場景下的最優推薦，如下圖。在推薦系統領域，這類模型的典型代表就是排序學習（Learn to Rank，LTR）[10](https://lumingdong.cn/cooperative-recommendation-algorithms.html#dfref-footnote-10)，通常用在推薦架構中的排序階段，關于 LTR，可以參考我的另一篇文章??[推薦系統中的排序學習](https://lumingdong.cn/learning-to-rank-in-recommendation-system.html)。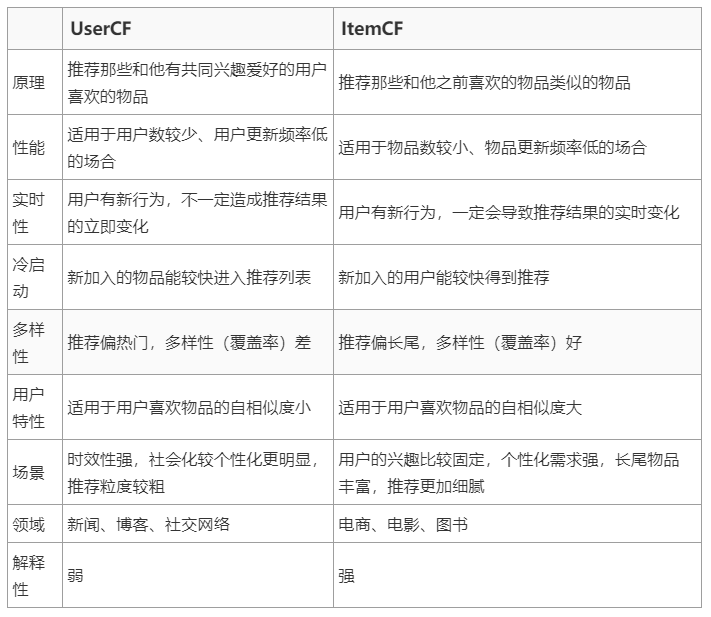 *  * ## **6. UserCF和ItemCF的區別** * 基于用戶的協同過濾和基于物品的協同過濾雖然很相似，但是在實際使用中，區別還是非常大的，下面總結了二者的主要區別，也是在實際應用中兩種算法的擇優選擇依據。就目前工業界來看，使用 ItemCF 要比使用 UserCF 要多很多。 *  ## **7. 工程經驗** 1. **只有原始用戶行為日志，如何從中構造出矩陣？** 我們在做協同過濾計算時，所用的矩陣是稀疏的，這樣帶來一個好處是：其實很多矩陣元素不用存，因為是 0。 稀疏矩陣有專門的存儲數據結構，這里介紹典型的稀疏矩陣存儲格式[11](https://lumingdong.cn/cooperative-recommendation-algorithms.html#dfref-footnote-11)。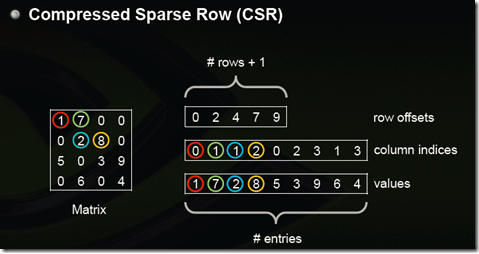 1）CSR：這個存儲稍微復雜點，是一個整體編碼方式。它有三個組成：數值、列號和行偏移共同編碼。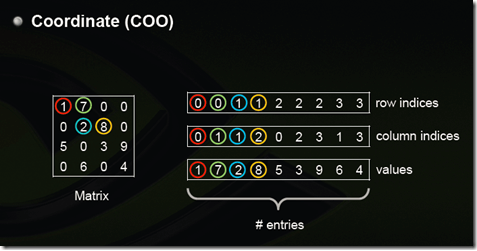 *  * 2）COO：這個存儲方式很簡單，每個元素用一個三元組表示（行號，列號，數值），只存儲有值的元素，缺失值不存儲。 *  * 這些存儲格式，在常見的計算框架里面都是標準的，如 Spark 中，Python 的 NumPy 包中。一些著名的算法比賽也通常都是以這種格式提供數據。 * 因此，把原始行為日志轉換成上面的格式，就可以使用常用計算框架的標準輸入了。 2. **如果用戶的向量很長，計算一個相似度要耗時很久，或者遇到用戶量很大，兩兩計算用戶相似度也很耗時，怎么辦？** * 協同過濾算法是很大程度依賴于相似度計算的，因此相似度計算性能優化是一個非常重要的課題，上面在講到協同過濾改進和變種算法時已經講到過一種由騰訊發表的實時相似度計算方法，下面我們看看其他可優化的方法， * * 首先是單個相似度計算問題，如果碰上向量很長，無論什么相似度計算方法，都要遍歷向量，如果用循環實現就更可觀了，所以通常降低相似度計算復雜度的辦法有兩種。 * 1. 對向量采樣計算。道理很簡單，兩個一百維的向量計算出的相似度是 0.7，我現在忍受一些精度的損失，不用 100 維計算，隨機從中取出 10 維計算，得到相似度是 0.72，顯然用 100 維計算出的 0.7 更可信一些，但是在計算復雜度降低十倍的情形下，0.72 和它誤差也不大，后者更經濟。這個算法由 Twitter 提出，叫做**DIMSUM（Dimension Independent Matrix Square using MapReduce）**算法，已經在 Spark 中實現了。 * 2. 向量化計算。與其說這是一個小技巧，不如說這是一種思維方式。在機器學習領域，向量之間的計算是家常便飯，難道向量計算都要用循環實現嗎？并不是，現代的線性代數庫都支持直接的向量運算，比循環快很多。也就是我們在任何地方，都要想辦法把循環轉換成向量來直接計算，一般像常用的向量庫都天然支持的，比如 Python 的 NumPy 。 * 其次的問題就是，如果用戶量很大，兩兩之間計算相似度代價就很大。 * * 有兩個辦法來緩解這個問題： * * 第一個辦法是：將相似度計算拆成 Map Reduce 任務，將原始矩陣 Map 成鍵為用戶對，值為兩個用戶對同一個物品的評分之積，Reduce 階段對這些乘積再求和，Map Reduce 任務結束后再對這些值歸一化； * * 第二個辦法是：不用基于用戶的協同過濾。 * * 另外，這種計算對象兩兩之間的相似度的任務，如果數據量不大，一般來說不超過百萬個，然后矩陣又是稀疏的，那么有很多單機版本的工具其實更快，比如 KGraph、 GraphCHI 等。 3. **在計算推薦時，需要為每一個用戶計算他和每一個物品的分數，如何提高效率？** * 得到了用戶之間的相似度之后。接下來還有一個硬骨頭，計算推薦分數。顯然，為每一個用戶計算每一個物品的推薦分數，計算次數是矩陣的所有元素個數，這個代價，你當然不能接受啊。這時候，有這么幾個特點我們可以來利用一下： * * 1）只有相似用戶喜歡過的物品需要計算，這個數量相比全部物品少了很多； * 2）把計算過程拆成 Map Reduce 任務。 * * 拆 Map Reduce 任務的做法是： * * 1）遍歷每個用戶喜歡的物品列表； * 2）獲取該用戶的相似用戶列表； * 3）把每一個喜歡的物品 Map 成兩個記錄發射出去，一個是鍵為 三元組，可以拼成一個字符串，值為 ，另一個是鍵為 三元組，值為 ，其中的 1 和 0 為了區分兩者，在最后一步中會用到； * 4）Reduce 階段，求和后輸出； * 5） 的值除以 的值 * 一般來說，中小型公司如果沒有特別必要的話，不要用分布式計算，看上去高大上、和大數據沾上邊了，實際上得不償失。 * * 拆分 Map Reduce 任務也不一定非要用 Hadoop 或者 Spark 實現。也可以用單機實現這個過程。 * * 因為一個 Map 過程，其實就是將原來耦合的計算過程解耦合了、拍扁了，這樣的話我們可以利用多線程技術實現 Map 效果。例如 C++ 里面 OpenMP 庫可以讓我們無痛使用多線程，充分剝削計算機所有的核。 4. **當算法輸入的樣本數據量較大時，算法的運行時間可以依靠工程技巧進行降低，下面介紹一些在基于 Spark 預測用戶喜歡商品時的一些工程技巧**。 **序列化和反序列化** * 輸入樣本中，用戶和商品可能以不同的字符表示，比如用戶 ID 可能是 32 位的字符串，如`5aec08bc4c953feb440896804535a46d`，而商品可能是數字，如`10057309`。樣本數據格式統一整齊，在內存中計算時能夠加快計算速度。 * 因此，可以考慮對用戶 ID 和商品 ID 進行序列化，映射到同一數據類型，比如長整型。通過長整型計算完后再反序列化映射到用戶 ID 和商品 ID 原有的類型。 **數據傾斜** * 在 shuffle 類型的算子，如 join 操作，在計算過程中會將相同的 key 數據分配的同一個 partition，當 key 相關的數據條數分布不均時，部分 partition 中的 key 的樣本條數是其他 partition 數據條數的 10 倍甚至更多，這樣數據條數多的 partition 對應的計算任務 task 就會花費大量的時間進行計算，拉長算法的執行時間。 * 對這種 key 下樣本條數分布嚴重不均勻的情況，可以考慮用隨機前綴和擴容 RDD 進行 join 等策略。 **廣播變量** * 在使用 Spark 進行計算時，會遇到需要在算子函數中使用外部變量的場景（尤其是大變量，比如 100M 以上的大集合），那么此時就應該使用 Spark 的廣播（Broadcast）功能來提升性能。 **map-side 預聚合** * 所謂的 map-side 預聚合，說的是在每個節點本地對相同的 key 進行一次聚合操作，類似于 MapReduce 中的本地 combiner。map-side 預聚合之后，每個節點本地就只會有一條相同的 key，因為多條相同的 key 都被聚合起來了。其他節點在拉取所有節點上的相同 key 時，就會大大減少需要拉取的數據數量，從而也就減少了磁盤 IO 以及網絡傳輸開銷。通常來說，在可能的情況下，建議使用 reduceByKey 或者 aggregateByKey 算子來替代掉 groupByKey 算子。因為 reduceByKey 和 aggregateByKey 算子都會使用用戶自定義的函數對每個節點本地的相同 key 進行預聚合。而 groupByKey 算子是不會進行預聚合的，全量的數據會在集群的各個節點之間分發和傳輸，性能相對來說比較差。 **Top40 VS. Top200** * 在預測用戶感興趣商品時，先尋找每個商品相似的商品，再尋找用戶喜歡的商品。每個商品相似的商品的數據集，作為尋找用戶喜歡的商品的輸入數據集。 * 選擇每個商品相似商品的個數不同，會影響最終用戶喜歡商品的集合，以及尋找用戶喜歡商品的計算時間。在實驗中發現，選擇 Top40 的相似商品和選擇 Top200 的相似商品，在最終尋找到用戶喜歡商品的的集合中，按照喜好程度排序的 Top40 的商品基本一致，但尋找用戶喜歡商品的計算時間有效減少了。 * 因此，選擇較合適相似商品的個數，能夠平衡最終用戶喜歡商品集合的效果，和尋找用戶喜歡商品的計算時間。 ## **8. 算法優缺點** * 協同過濾是業界使用非常多的推薦算法，可以說是一個經過了時間檢驗的算法。協同過濾算法本身其實對于推薦什么物品是一點都不關心的，所有的推薦機制都是基于用戶對物品的行為來制定的，這也造就了協同過濾在有很多優點的同時，缺點也依然非常明顯。我們來簡單看一下協同過濾算法的優缺點。 **協同過濾算法的優點** 1. 基于用戶行為，因此對推薦內容無需先驗知識 2. 只需要用戶和商品的關聯矩陣即可，結構簡單 3. 在用戶行為豐富的情況下，效果好 **基于協同推薦算法的缺點** 1. 需要大量的顯性/隱形的用戶行為，有冷啟動問題 2. 假定用戶的興趣完全取決于之前的行為，沒有考慮到當前的上下文環境 3. 需要通過完全相同的商品關聯，相似的不行 4. 在數據稀疏的情況下易受影響，可以考慮二度關聯。 **補充說明** * 缺點中的第三條，有時稱為同義詞（Synonymy）問題，即在實際應用中，不同的項目名稱可能對應相似的項目（比如同款商品），基于相似度計算的推薦系統不能發現這樣的潛在關系，而是把它們當不同的項目對待（同款商品本來對應同一個商品，但計算相似度的時候是按照不同商品計算的）。 ## **9. 解決協同過濾的冷啟動** * 可以說，冷啟動是協同過濾的一個致命弱點，這里我們看一些簡單的方法[3](https://lumingdong.cn/cooperative-recommendation-algorithms.html#dfref-footnote-3-1)，因為冷啟動問題是推薦系統中的一個重要課題，之后有時間我會單獨總結一篇文章。 **對于新用戶** * 所有推薦系統對于新用戶都有這個問題 * 推薦非常熱門的商品，收集一些信息 * 在用戶注冊的時候收集一些信息 * 在用戶注冊完之后，用一些互動游戲等確定喜歡與、喜歡 **對于新商品** * 根據本身的屬性，求與已有商品的相似度。 * Item-based 協同過濾可以推薦出去。 ## **10. 應用場景** * 協同過濾的應用場景非常廣泛，并且推薦效果和復雜度都是可以讓人接受的，基于協同過濾算法通常可以作為一個穩定的 Baseline 推薦系統，在電商領域最為常見。 ## **11. 業界案例** * **亞馬遜**：最早使用 ItemCF 算法的電商網站； * * **Digg**：新聞類網站，使用 UserCF； * * **Hulu**：視頻類網站； * * **京東、淘寶、當當**：電商中買了又買、看了又看、購買過此商品的顧客還購買過。