[TOC]
## **1. k近鄰算法的基本概念,原理以及應用**
* k近鄰算法是一種**基本分類和回歸方法**。本篇文章只討論分類問題的k近鄰法。
* K近鄰算法,即是給定一個訓練數據集,對新的輸入實例,在訓練數據集中找到與該實例**最鄰近**的K個實例,**這K個實例的多數屬于某個類**,就把該輸入實例分類到這個類中。(**這就類似于現實生活中少數服從多數的思想**)根據這個說法,咱們來看下引自維基百科上的一幅圖:
* :-: 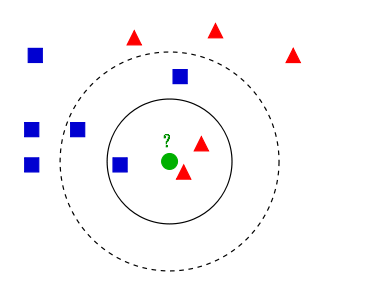
* 如上圖所示,有**兩類**不同的樣本數據,分別用藍色的小正方形和紅色的小三角形表示,而圖正中間的那個綠色的圓所標示的數據則是**待分類的數據**。這也就是我們的目的,來了一個新的數據點,我要得到它的類別是什么?好的,下面我們根據k近鄰的思想來給綠色圓點進行分類。
* 如果K=3,綠色圓點的最鄰近的3個點是2個紅色小三角形和1個藍色小正方形,**少數從屬于多數,** 基于統計的方法,判定綠色的這個待分類點屬于紅色的三角形一類。
* 如果K=5,綠色圓點的最鄰近的5個鄰居是2個紅色三角形和3個藍色的正方形,**還是少數從屬于多數,** 基于統計的方法,判定綠色的這個待分類點屬于藍色的正方形一類。
* 通過上面的例子也能夠看出,KNN并不需要事先訓練一個模型,而是直到需要分類測試樣本時才進行。這種學習方法叫做 懶惰學習(lazy learning),這類技術在訓練階段僅僅把樣本保存起來,訓練時間開銷為0,待收到測試樣本時再處理。而且我們講過的神經網絡,決策樹,logistic 回歸,SVM等在訓練階段就學習模型的方法,稱為急切學習(eager learning)。下面稍微形式化一點用偽代碼來描述下KNN分類算法的流程:
* 
* 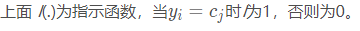
* 這里加一句題外話,KNN雖然思想簡單,但是性能是很不錯的,**能夠理論證明KNN的泛化錯誤率不超過貝葉斯最優分類器的錯誤率的兩倍。** 從以上的基本原理中,我們大概能夠得到KNN算法的三個關鍵點:
* 1. **K值的大小對預測結果的影響**
* 2. **距離度量方式**
* 3. **如何找到與測試樣本距離最近的K個樣本**
* 下面會分別介紹這三方面的內容。
## **2. KNN中K值大小對預測結果的影響**
* ? ? ? ?從上面原理中,能夠知道KNN中K值是需要自己指定的,關于K值大小對預測結果的影響如下:
* 若K值太小,相當于用較小的鄰域中的訓練樣本去預測,則KNN分類器容易受到由于訓練數據中噪聲的影響而產生過擬合。
* 若K值太大,因為鄰域比較大,則與測試樣本距離較遠的訓練樣本也會起作用,這樣會導致誤分類測試樣本。
* 若K=N,那么無論輸入的測試樣本是什么,輸出都會是訓練樣本中樣本數量最多的類,這種模型基本沒什么用。
* **在實際應用中,k值一般選取一個比較小的值,可以通過交叉驗證法來選取最優的K值。**
## **3. KNN中距離度量方式**
* 在上文中說到,k近鄰算法是在訓練數據集中找到與該實例**最鄰近**的K個實例,這K個實例的多數屬于某個類,我們就說預測點屬于哪個類。
* 定義中所說的最鄰近是如何度量呢?我們怎么知道誰跟測試點最鄰近。這里就會引出我們幾種度量倆個點之間距離的標準。
* 我們可以有以下幾種度量方式:
* 
* 其中當p=2的時候,就是我們最常見的歐式距離,我們也一般都用歐式距離來衡量我們高維空間中倆點的距離。在實際應用中,距離函數的選擇應該根據數據的特性和分析的需要而定,一般選取p=2歐式距離表示。
## **4. 特征歸一化的必要性**
* 首先舉例如下,我用一個人身高(cm)與腳碼(尺碼)大小來作為特征值,類別為男性或者女性。我們現在如果有5個訓練樣本,分布如下:
* A \[(179,42),男\] B \[(178,43),男\] C \[(165,36)女\] D \[(177,42),男\] E \[(160,35),女\]
* 通過上述訓練樣本,很容易看到第一維身高特征是第二維腳碼特征的4倍左右,那么在進行距離度量的時候,**我們就會偏向于第一維特征。**這樣造成倆個特征并不是等價重要的,最終可能會導致距離計算錯誤,從而導致預測錯誤。舉例如下:
* 現在來了一個測試樣本 F(167,43),讓我們來預測他是男性還是女性,我們采取k=3來預測。
* 下面我們用歐式距離分別算出F離訓練樣本的歐式距離,然后選取最近的3個,多數類別就是我們最終的結果,計算如下:
* 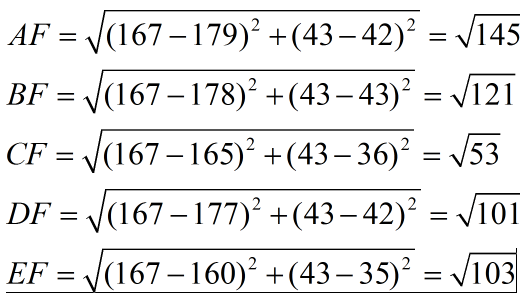
* 由計算可以得到,最近的前三個分別是C,D,E三個樣本,那么由C,E為女性,D為男性,女性多于男性得到我們要預測的結果為**女性**。
* **這樣問題就來了,一個女性的腳43碼的可能性,遠遠小于男性腳43碼的可能性,那么為什么算法還是會預測F為女性呢?那是因為由于各個特征量綱的不同,在這里導致了身高的重要性已經遠遠大于腳碼了,這是不客觀的。** 所以我們應該讓每個特征都是同等重要的!這也是我們要歸一化的原因!歸一化公式如下:
* 
## **5. k近鄰算法中的分類決策規則**
* k近鄰算法的分類決策規則通俗來說就是**k 近鄰法中的分類決策規則往往是多數表決決定,背后的數學思維是什么?**
* k 近鄰法中的分類決策規則往往是多數表決,即由輸入實例的 k 個近鄰的訓練實例中的多數類決定輸入實例的類。
* 多數表決規則(majority voting rule)有如下解釋:如果分類的損失函數為 0-1 損失函數,分類函數為:
* :-: 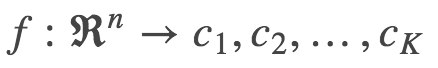
* 那么誤分類的概率是:
* :-: 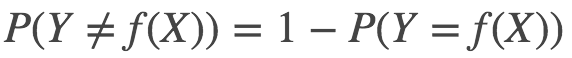
* 
* 換句話說,目前候選種類為c1,c2....cj,我選擇哪一個,使得我們的經驗風險最小(**經驗風險通俗講就是訓練數據的錯誤值**)。
* 那么由上式經驗風險最小,**也就是說,要我們預測出的種類屬于cj類的最多(那么預測出來的種類結果和真實結果一致的越多,我們認為正確可能性就越大,也就是經驗風險越小),也就是我們所說的多數表決規則。而它也等價于我們的經驗風險最小。這也是我們在k近鄰算法中采用多數表決規則的正確性說明!**
## **6. k近鄰法的實現:kd樹原理的講解以及kd樹詳細例子**
### **kd樹原理**
**kd 樹的結構**
* kd樹是一個二叉樹結構,它的每一個節點記載了【**特征坐標,切分軸,指向左枝的指針,指向右枝的指針**】。
* 其中,特征坐標是線性空間 Rn 中的一個點 (x1,x2,…,xn)切分軸由一個整數 r 表示,這里 1≤r≤n,是我們在 n 維空間中沿第 rr維進行一次分割。節點的左枝和右枝分別都是 kd 樹,并且滿足:如果 y 是左枝的一個特征坐標,那么 yr≤xr(**左分支結點**);并且如果 z 是右枝的一個特征坐標,那么 zr≥xr(**右分支結點**)。
* 給定一個數據樣本集 S?Rn 和切分軸 r,以下**遞歸算法**將構建一個基于該數據集的 kd 樹,每一次循環制作一個節點:
> ?? 如果 |S|=1,記錄 S 中唯一的一個點為當前節點的特征數據,并且不設左枝和右枝。(|S| 指集合 S 中元素的數量)
> ?? 如果 |S|>1
> * 將 S 內所有點按照第 r 個坐標的大小進行**排序**;
> * 選出該排列后的中位元素(**如果一共有偶數個元素,則選擇中位左邊或右邊的元素,左隨便哪一個都無所謂**),作為當前節點的特征坐標,并且記錄切分軸 r;
>
> * 將 SL設為在 S 中所有排列在中位元素之前的元素; SR 設為在 S 中所有排列在中位元素后的元素;
>
> * 當前節點的左枝設為以 SL 為數據集并且 r 為切分軸制作出的 kd 樹;當前節點的右枝設為以 SR 為數據集并且 r為切分軸制作出的 kd 樹。再設 r←(r+1)modn。(**這里,我們想輪流沿著每一個維度進行分割;modn 是因為一共有 n 個維度,**在**沿著最后一個維度進行分割之后再重新回到第一個維度。**)
>
### **kd樹的構建**
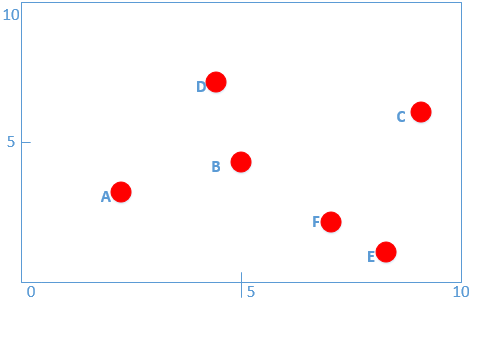
* **給定一個二維空間的數據集:**
* **T = {(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)}, 構造一個平衡kd樹。**
* **為了方便,我這里進行編號A(2,3)、B(5,4)、C(9,6)、D(4,7)、E(8,1)、F(7,2)**
* **初始值r=0,對應x軸。**
* 可視化數據點如下:
* :-: 
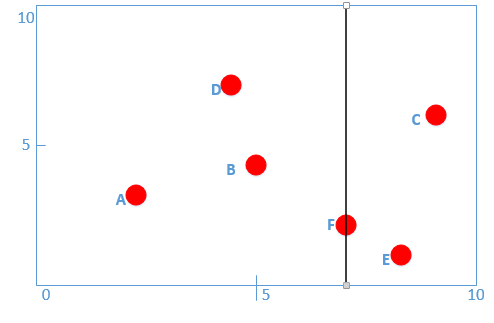
* 首先先沿 x 坐標進行切分,我們選出 x 坐標的中位點,獲取最根部節點的坐標,對數據點x坐標進行排序得:
* A(2,3)、D(4,7)、B(5,4)、F(7,2)、E(8,1)、C(9,6)
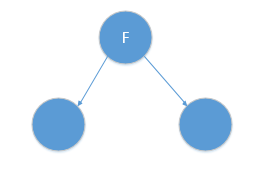
* **則我們得到中位點為B或者F,我這里選擇F作為我們的根結點,并作出切分(并得到左右子樹),如圖:**
* :-: 
* **對應的樹結構如下:**
* :-: 
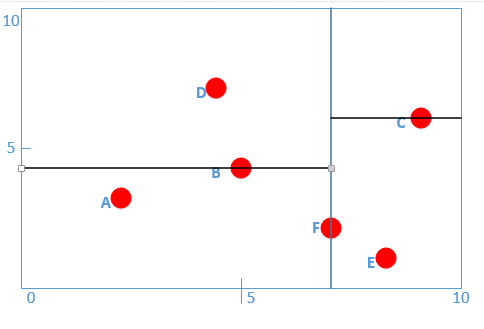
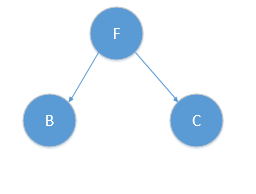
* **根據算法,此時r=r+1=1,對應y軸,此時對應算法|S|>1,則我們分別遞歸的在F對應的左子樹與右子樹按y軸進行分類,得到中位節點分別為B,C點,如圖所示:**
* :-: 
* **對應樹結構為:**
* :-: 
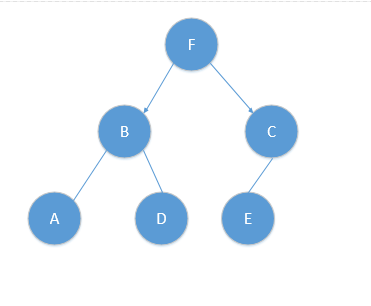
* **而到此時,B的左孩子為A,右孩子為D,C的左孩子為E,均滿足|S|==1,此時r = (r+1)mod2 = 0,又滿足x軸排序,對x軸劃分!則如圖所示:**
* :-: 
* 對應樹結構如下:
* :-: 
* 到這里為止,給定的kd樹構造完成啦,**所有的數據點都能在樹上的每個結點找到!**而我們根據上面構造樹的過程,也能很容易的知道,來了一個新的數據點的時候,對應該層的指定維數,通過比較大小,我就能知道往左(**預測點對應維度數據小于該結點對對應維度數據**)走還是往右(**預測點對應維度數據大于該結點對應維度數據**)走,**那么好的情況下**,就能省掉一半的數據點啦~(**不好的情況,沒有節省,后面會說到,這也是kd樹的致命缺點~**)
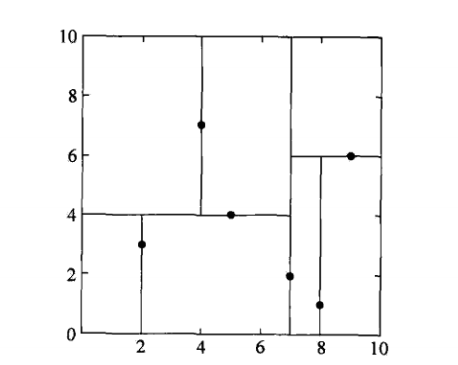
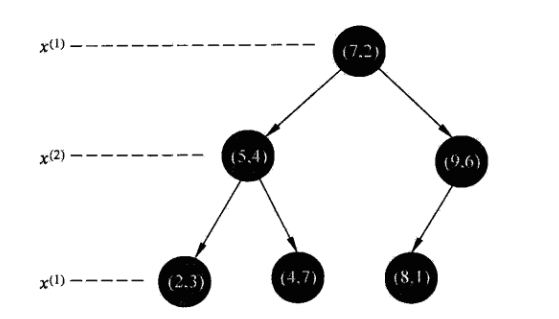
* 這也是李航博士書籍上例子中kd樹構造的詳細過程!他的圖片如下:
* :-: 
* 對應kd樹為:
* :-: 
### **kd樹搜索**
* 我這里和統計學習方法例子一樣,以最近鄰為例加以敘述,同樣的方法可以應用到k近鄰。
* **為了讓大家更好的理解,我這里直接用上面例子給大家一步一步給出過程!**
* **首先我們來看用kd樹的最近鄰搜索算法流程:**
* **輸入:已構造的kd樹;目標點x;**
* **輸出:x的最近鄰.**
* (1)在kd樹中找出包含目標點x的葉結點:從根結點出發,遞歸地向下訪問kd樹,**若目標點x當前維的坐標小于切分點的坐標,則移動到左子節點,否則移動到右子結點.直到子結點為葉結點位置.**
* (2)以此葉結點為“當前最近點”
* (3)遞歸地向上回退,在每個結點進行以下操作:
* * (a)如果該結點保存的實例點比當前最近點距離目標點更近,則以該實例點為“當前最近點”.
* * (b)當前最近點一定存在于該結點一個子結點對應的區域.檢查該子結點的父結點的另一個子結點對應的區域是否有更近的點.具體地,**檢查另一子結點對應的區域是否以目標點為球心、以目標點與“當前最近點”間為半徑的超球體相交。**
* **如果不相交,向上回退.**
* (4)**當回退到根結點時,搜索結束。最后的“當前最近點”即為最近鄰點.**
* 下面通過例子,一步一步走一遍上面所描述的算法過程,化抽象為具體!
* **kd樹最近鄰搜索例題:**
* **給定一個二維空間的數據集:**
* **T = {(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},輸入目標實例為K(8.5,1),求K的最近鄰。**
* **首先我們由上面可以給出,T的kd樹對應如下:**
* :-: 
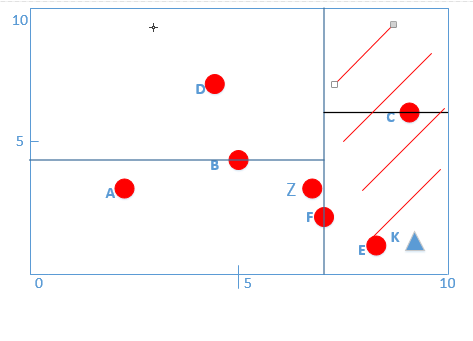
* 我們此時的K(8.5,1),根據算法第一步得:第一層的x軸K點為8大于F點的7,所以進入F(7,2)的右子樹,進入下面紅色線條區域:
* :-: 
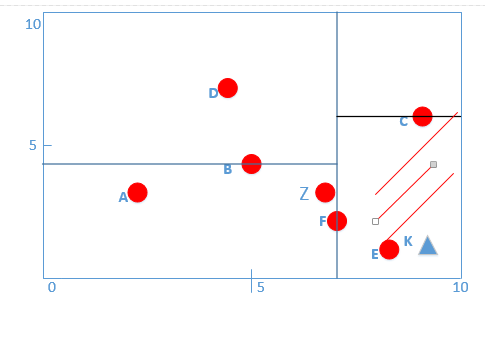
* 到了第二層,分割平面坐標為y軸,K點y軸坐標為1,小于C點y軸坐標6,則繼續向右走,在下圖紅色線條區域內:
* :-: 
* 則此時算法對應第(1)部分完成,我們找到了葉子節點E(8,1)。
* 我們進行算法第(2)步,把E(8,1)作為最近鄰點。此時我們算一下KE之間的距離為0.5(便于后面步驟用到).
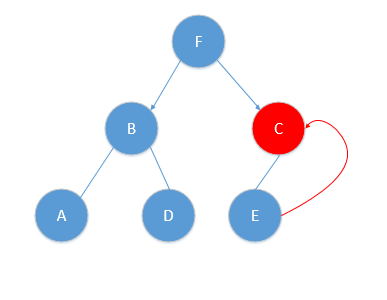
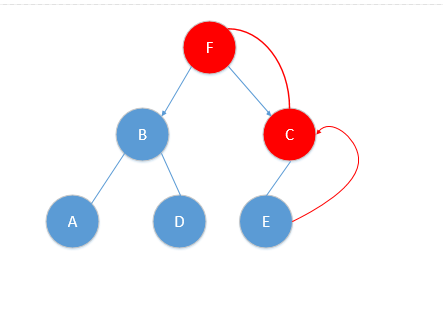
* 然后進行算法第(3)步,遞歸的往上回退,每個結點進行相同步驟,好,我現在從E點回退到C點,對應圖片如下;
*
* :-: 
*
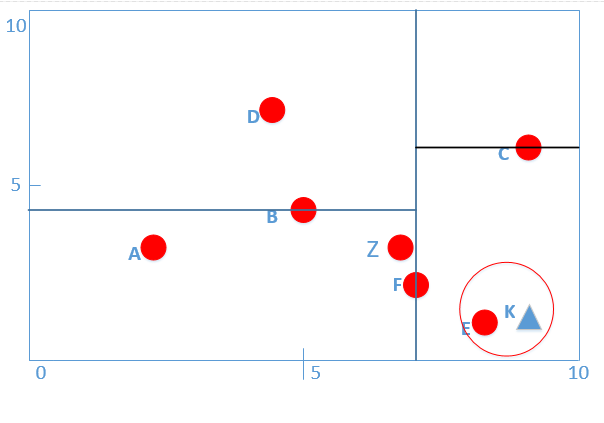
* 此時對C點進行第(3)步的(a)操作,判斷一下KC距離與保存的最近鄰距離(這時是KE)比較,KC距離為點K(8.5,1)與點C(9,6)之間的距離![[公式]](https://www.zhihu.com/equation?tex=%5Csqrt%7B25.25%7D+)\>最近鄰0.5,于是不更新最近鄰點。
*
* 然后對C點進行第(3)步的(b)操作,判斷一下當前最近鄰的距離畫一個圓是否與C點切割面相交,如圖所示:
*
* :-: 
*
* 我們很容易看到與C點切割面并沒有相交,于是執行由C點回退到它的父結點F點。如圖:
*
* :-: 
*
* 對F點進行(a),(b)操作!
* 進行(a)步驟,判斷FK的距離是否小于當前保存的最小值,FK=![[公式]](https://www.zhihu.com/equation?tex=%5Csqrt%7B%287-8.5%29%5E%7B2%7D%2B%282-1%29%5E%7B2%7D+%7D%3D%5Csqrt%7B1.25%7D++)\>0.5,所以不改變最小距離
* 下面我們進行(b)步驟,為了判斷F點的另一半區域是否有更小的點,判斷一下當前最近鄰的距離畫一個圓是否與F點切割面相交,如圖所示:
* :-: 
* **發現與任何分割線都沒有交點,那么執行算法最后一步,此時F點已經是根結點,無法進行回退,那么我們可以得到我們保留的當前最短距離點E點就是我們要找的最近鄰點!任務完成,**
* **并且根據算法流程,我們并沒有遍歷所有數據點,而是F點的左孩子根本沒有遍歷,節省了時間,但是并不是所有的kd樹都能到達這樣的效果。**
## **7. kd樹的不足以及最差情況舉例**
* 講解這個知識點,還是通過一個例子來直觀說明!
* **給定一個二維空間的數據集:**
* **T = {(2,3),(5,4),(9,6),(4,7),(8,1),(7,2)},輸入目標實例為K(8,3),求K的最近鄰。**
* **首先我們由上面可以給出,T的kd樹對應如下:**
*
* :-: 
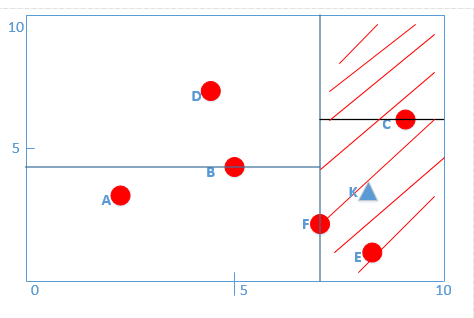
* **我們此時的K(8,3),根據算法第一步得:第一層的x軸K點為8大于F點的7,所以進入F(7,2)的右子樹,進入下面紅色線條區域:**
*
* :-: 
*
* **(注意:這里葉子節點畫不畫分割線都沒有關系!)**
*
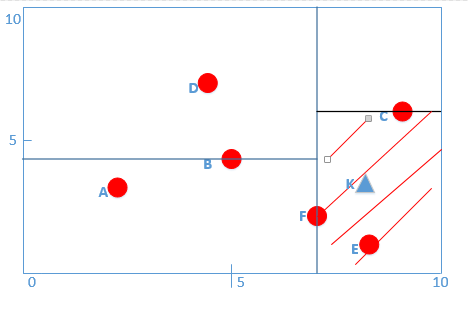
* **到了第二層,分割平面坐標為y軸,K點y軸坐標為3,小于C點y軸坐標6,則繼續向右走,在下圖紅色線條區域內:**
*
* :-: 
*
* **則此時算法對應第(1)部分完成,我們找到了葉子節點E(8,1)。**
*
* **我們進行算法第(2)步,把E(8,1)作為最近鄰點。此時我們算一下KE之間的距離為2(便于后面步驟用到).**
*
* **然后進行算法第(3)步,遞歸的往上回退,每個結點進行相同步驟,好,我現在從E點回退到C點,對應圖片如下;**
*
* :-: 
*
* **此時對C點進行第(3)步的(a)操作**,判斷一下KC距離與保存的最近鄰距離(這時是KE)比較,KC距離為點K(8,3)與點C(9,6)之間的距離![[公式]](https://www.zhihu.com/equation?tex=%5Csqrt%7B10%7D+)\>最近鄰2,于是不更新最近鄰點。
*
* **然后對C點進行第(3)步的(b)操作,判斷一下當前最近鄰的距離畫一個圓是否與C點切割面相交,如圖所示:**
*
* :-: 
*
* **我們很容易看到與C點切割面并沒有相交,于是執行由C點回退到它的父結點F點。如圖:**
*
* :-: 
*
* **對F點進行(a),(b)操作!**
*
* **進行(a)步驟,判斷FK的距離是否小于當前保存的最小值,FK=![[公式]](https://www.zhihu.com/equation?tex=%5Csqrt%7B%287-8%29%5E%7B2%7D%2B%282-3%29%5E%7B2%7D+%7D%3D%5Csqrt%7B2%7D++)**
*
* **<2,所以將最小距離替換為FK的距離!**
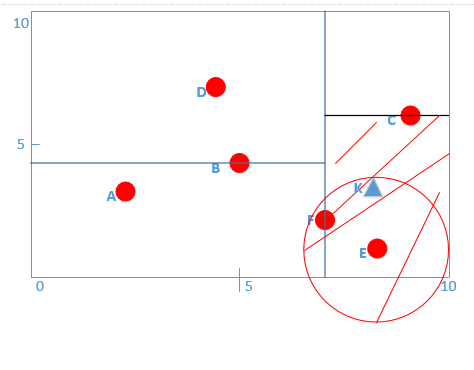
* **下面我們進行(b)步驟,為了判斷F點的另一半區域是否有更小的點,** 判斷一下當前最近鄰的距離畫一個圓是否與F點切割面相交,如圖所示:
*
* :-: 
*
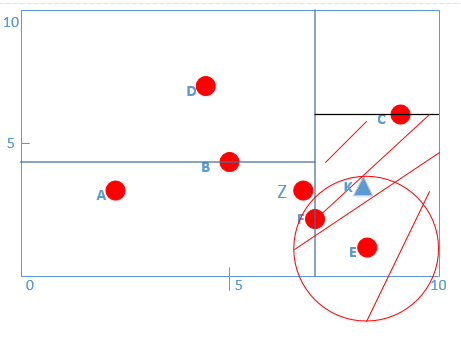
* 我們可以看出,此時圓與F點有交點,那么說明F點左側是有可能存在與K點距離更小的點(注:這里我們人為看起來好像沒有,但是計算機不知道,必須搜索下去,只要以當前最小值畫圓發現與節點切割面有交點,**那么一定要進行搜索,不然數據如果是下圖:)**
*
* :-: 
*
* 如果不進行搜索,我們就可能會漏掉Z數據點,因為KZ比當前最小值KF小!
*
* 此時相交,我們就需要再F點的左孩子進行搜索,一直搜索到葉子節點A,然后進行(a),(b)步驟,繼續回溯到它的父親結點B,以及最后到達F點,完成最后的最近鄰是F點,這里幾乎遍歷了所有數據點,**幾乎退化了為線性時間0(n)了。這也是kd樹的最差的情況。**
*
*
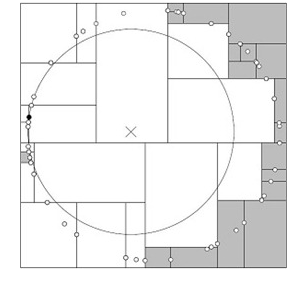
* 當給定的數據分布很差的時候,我們每一次計算畫圓過程中,**都會與每一個分割面相交的時候,都會遞歸搜索到該結點的另一個子空間中遍歷,那么這樣最壞的情況是進行線性時間搜索!**比如構建的kd樹和數據分布如下:
*
* :-: 
*
* **如圖所示,我們可以看到幾乎所有的數據離給定預測的點距離很遠,每次進行算法第三步判斷是否與分割面有交點的時候,幾乎每個面都有交點,只要有交點,就必須將該點的另一半結點遍歷到葉子結點,重復的進行算法步驟,導致了搜索的低效!**
## **8. k近鄰方法的一些優缺點總結**
* **優點:**
*
* 1. KNN分類方法是一種非參數的分類技術,簡單直觀,易于實現!**只要讓預測點分別和訓練數據求距離,挑選前k個即可,非常簡單直觀。**
*
* 2. KNN是一種在線技術,新數據可以直接加入數據集而**不必進行重新訓練**
*
* **缺點及改進**:
* 1. 當樣本不平衡時,**比如一個類的樣本容量很大,其他類的樣本容量很小**,輸入一個樣本的時候,K個鄰近值大多數都是大樣本容量的那個類,這時可能會導致分類錯誤。
* **改進方法:對K鄰近點進行加權,也就是距離近的權值大,距離遠的點權值小。**
*
2. 計算量較大,每個待分類的樣本都要計算它到全部點的距離**,根據距離排序才能求得K個臨近點。
* **改進方法:先對已知樣本帶你進行裁剪,事先去除分類作用不大的樣本,采取kd樹以及其它高級搜索方法BBF等算法減少搜索時間。**
