[TOC] * 在數據處理中，經常會遇到特征維度比樣本數量多得多的情況，如果拿到實際工程中去跑，效果不一定好。一是因為冗余的特征會帶來一些噪音，影響計算的結果；二是因為無關的特征會加大計算量，耗費時間和資源。所以我們通常會對數據重新變換一下，再跑模型。**數據變換的目的不僅僅是降維，還可以消除特征之間的相關性，并發現一些潛在的特征變量。** ## 一、PCA的目的 * ?PCA是一種在盡可能減少信息損失的情況下找到某種方式降低數據的維度的方法。通常來說，我們期望得到的結果，是把原始數據的特征空間（n個d維樣本）投影到一個小一點的子空間里去，并盡可能表達的很好（就是說損失信息最少）。常見的應用在于模式識別中，我們可以通過減少特征空間的維度，抽取子空間的數據來最好的表達我們的數據，從而減少參數估計的誤差。注意，主成分分析通常會得到協方差矩陣和相關矩陣。這些矩陣可以通過原始數據計算出來。協方差矩陣包含平方和與向量積的和。相關矩陣與協方差矩陣類似，但是第一個變量，也就是第一列，是標準化后的數據。**如果變量之間的方差很大，或者變量的量綱不統一，我們必須先標準化再進行主成分分析。** ## 二、PCA VS MDA * 提到PCA，可能有些人會想到MDA（Multiple Discriminate Analysis,多元判別分析法），這兩者都是線性變換，而且很相似。只不過在PCA中，我們是找到一個成分（方向）來把我們的數據最大化方差，而在MDA中，我們的目標是最大化不同類別之間的差異（比如說，在模式識別問題中，我們的數據包含多個類別，與兩個主成分的PCA相比，這就忽略了類別標簽）。 * ?換句話說，通過PCA，我們把整個數據集（不含類別標簽）投射到一個不同的子空間中，在MDA中，我們試圖決定一個合適的子空間來區分不同類別。再換種方式說，PCA是找到數據傳播最廣的時候的最大方差的軸axis，MDA是最大化類別與類別之間的區別。 * 上文我們提到了子空間，那么怎么樣去尋找“好的”子空間呢？ * 假設我們的目標是減少d維的數據集，將其投影到k維的子空間上（看k<d）。所以，我們如何來確定k呢？如何知道我們選擇的特征空間能夠很好的表達原始數據呢？ * 下文中我們會計算數據中的特征向量（主成分），然后計算散布矩陣（[scatter\_matrix](https://en.wikipedia.org/wiki/Scatter_matrix)）中（也可以從協方差矩陣中計算）。每個特征向量與特征值相關，即特征向量的“長度”或“大小”。如果發現每個特征值都很小，那就可以說明我們的原始數據就已經是一個“好的”空間了。但是，如果有些特征值比其他值要大得多，我們只需要關注那些特別大的特征值，因為這些值包含了數據分布情況的絕大部分信息。反之，那些接近于0的特征值包含的信息幾乎沒有，在新的特征空間里我們可以忽略不計。 ## 三、PCA的過程 * 通常來說有以下六步： > 1.去掉數據的類別特征（label），將去掉后的d維數據作為樣本 2.計算d維的均值向量（即所有數據的每一維向量的均值） 3.計算所有數據的散布矩陣（或者協方差矩陣） 4.計算特征值（e1,e2,...,ed）以及相應的特征向量（lambda1,lambda2,...,lambda d） 5.按照特征值的大小對特征向量降序排序，選擇前k個最大的特征向量，組成d\*k維的矩陣W（其中每一列代表一個特征向量） 6.運用d\*K的特征向量矩陣W將樣本數據變換成新的子空間。（用數學式子表達就是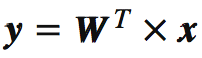，其中x是d\*1維的向量，代表一個樣本，y是K\*1維的在新的子空間里的向量） ### 1.數據準備----生成三維樣本向量 * 首先隨機生成40\*3維的數據，符合多元高斯分布。假設數據被分為兩類，其中一半類別為w1，另一半類別為w2 ``` #coding:utf-8 import numpy as np np.random.seed(4294967295) mu_vec1 = np.array([0,0,0]) cov_mat1 = np.array([[1,0,0],[0,1,0],[0,0,1]]) class1_sample = np.random.multivariate_normal(mu_vec1, cov_mat1, 20).T assert class1_sample.shape == (3,20)#檢驗數據的維度是否為3*20，若不為3*20，則拋出異常 mu_vec2 = np.array([1,1,1]) cov_mat2 = np.array([[1,0,0],[0,1,0],[0,0,1]]) class2_sample = np.random.multivariate_normal(mu_vec2, cov_mat2, 20).T assert class1_sample.shape == (3,20)#檢驗數據的維度是否為3*20，若不為3*20，則拋出異常 ``` * 運行這段代碼后，我們就生成了包含兩個類別的樣本數據，其中每一列都是一個三維的向量，所有數據是這樣的矩陣： * 結果：  ### 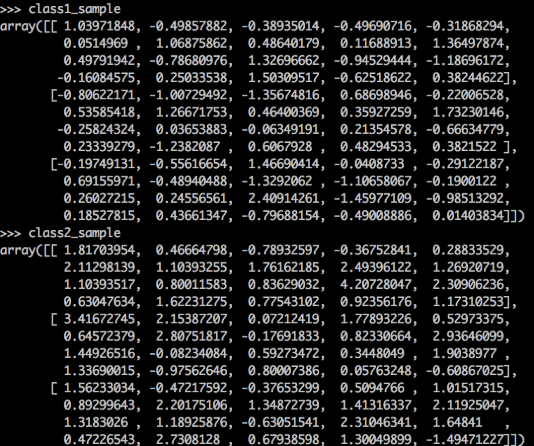2.作圖查看原始數據的分布 ``` from matplotlib import pyplot as plt from mpl_toolkits.mplot3d import Axes3D from mpl_toolkits.mplot3d import proj3d fig = plt.figure(figsize=(8,8)) ax = fig.add_subplot(111, projection='3d') plt.rcParams['legend.fontsize'] = 10 ax.plot(class1_sample[0,:], class1_sample[1,:], class1_sample[2,:], 'o', markersize=8, color='blue', alpha=0.5, label='class1') ax.plot(class2_sample[0,:], class2_sample[1,:], class2_sample[2,:], '^', markersize=8, alpha=0.5, color='red', label='class2') plt.title('Samples for class 1 and class 2') ax.legend(loc='upper right') plt.show() ``` * 　結果：  ### 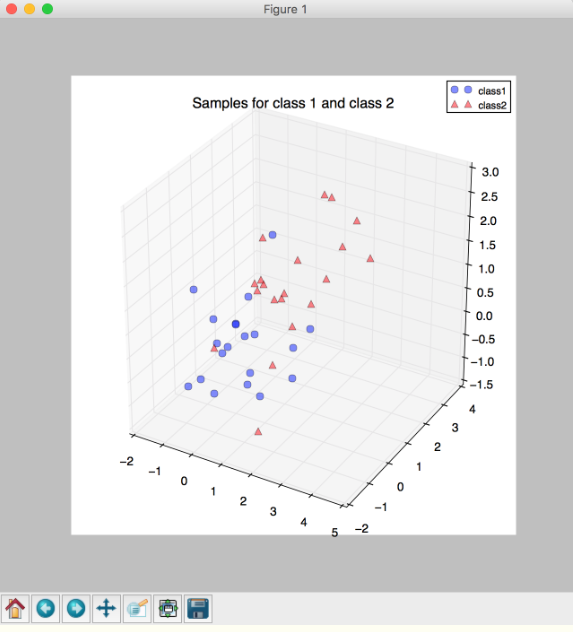3.去掉數據的類別特征 ``` 1 all_samples = np.concatenate((class1_sample, class2_sample), axis=1) 2 assert all_samples.shape == (3,40)#檢驗數據的維度是否為3*20，若不為3*20，則拋出異常 ``` ### 4.計算d維向量均值 ``` mean_x = np.mean(all_samples[0,:]) mean_y = np.mean(all_samples[1,:]) mean_z = np.mean(all_samples[2,:]) mean_vector = np.array([[mean_x],[mean_y],[mean_z]]) print('Mean Vector:\n', mean_vector) ``` * 結果： ``` 1 print('Mean Vector:\n', mean_vector) 2 Mean Vector:, 3 array([[ 0.68047077], 4 [ 0.52975093], 5 [ 0.43787182]])) ``` ### 5.計算散步矩陣或者協方差矩陣 * a.計算散步矩陣 * 散布矩陣公式： * 　　其中m是向量的均值：（第4步已經算出來是mean\_vector） ``` 1 scatter_matrix = np.zeros((3,3)) 2 for i in range(all_samples.shape[1]): 3 scatter_matrix += (all_samples[:,i].reshape(3,1) - mean_vector).dot((all_samples[:,i].reshape(3,1) - mean_vector).T) 4 print('Scatter Matrix:\n', scatter_matrix) ``` * 結果： ``` 1 print('Scatter Matrix:\n', scatter_matrix) 2 ('Scatter Matrix:, 3 array([[ 46.81069724, 13.95578062, 27.08660175], 4 [ 13.95578062, 48.28401947, 11.32856266], 5 [ 27.08660175, 11.32856266, 50.51724488]])) ``` * b.計算協方差矩陣 * 如果不計算散布矩陣的話，也可以用python里內置的numpy.cov()函數直接計算協方差矩陣。因為散步矩陣和協方差矩陣非常類似，散布矩陣乘以（1/N-1）就是協方差，所以他們的特征空間是完全等價的（特征向量相同，特征值用一個常數（1/N-1，這里是1/39）等價縮放了）。協方差矩陣如下所示： ``` 1 cov_mat = np.cov([all_samples[0,:],all_samples[1,:],all_samples[2,:]]) 2 print('Covariance Matrix:\n', cov_mat) ``` * 結果： ``` 1 >>> print('Covariance Matrix:\n', cov_mat) 2 Covariance Matrix:, 3 array([[ 1.20027429, 0.35784053, 0.69452825], 4 [ 0.35784053, 1.23805178, 0.29047597], 5 [ 0.69452825, 0.29047597, 1.29531397]])) ``` ### 6.計算相應的特征向量和特征值 ``` 1 # 通過散布矩陣計算特征值和特征向量 2 eig_val_sc, eig_vec_sc = np.linalg.eig(scatter_matrix) 3 4 # 通過協方差矩陣計算特征值和特征向量 5 eig_val_cov, eig_vec_cov = np.linalg.eig(cov_mat) 6 7 for i in range(len(eig_val_sc)): 8 eigvec_sc = eig_vec_sc[:,i].reshape(1,3).T 9 eigvec_cov = eig_vec_cov[:,i].reshape(1,3).T 10 assert eigvec_sc.all() == eigvec_cov.all() 11 12 print('Eigenvector {}: \n{}'.format(i+1, eigvec_sc)) 13 print('Eigenvalue {} from scatter matrix: {}'.format(i+1, eig_val_sc[i])) 14 print('Eigenvalue {} from covariance matrix: {}'.format(i+1, eig_val_cov[i])) 15 print('Scaling factor: ', eig_val_sc[i]/eig_val_cov[i]) 16 print(40 * '-') ``` * 結果： ``` 1 Eigenvector 1: 2 [[-0.84190486] 3 [-0.39978877] 4 [-0.36244329]] 5 Eigenvalue 1 from scatter matrix: 55.398855957302445 6 Eigenvalue 1 from covariance matrix: 1.4204834860846791 7 Scaling factor: 39.0 8 ---------------------------------------- 9 Eigenvector 2: 10 [[-0.44565232] 11 [ 0.13637858] 12 [ 0.88475697]] 13 Eigenvalue 2 from scatter matrix: 32.42754801292286 14 Eigenvalue 2 from covariance matrix: 0.8314755900749456 15 Scaling factor: 39.0 16 ---------------------------------------- 17 Eigenvector 3: 18 [[ 0.30428639] 19 [-0.90640489] 20 [ 0.29298458]] 21 Eigenvalue 3 from scatter matrix: 34.65493432806495 22 Eigenvalue 3 from covariance matrix: 0.8885880596939733 23 Scaling factor: 39.0 24 ---------------------------------------- ``` * 其實從上面的結果就可以發現，通過散布矩陣和協方差矩陣計算的特征空間相同，協方差矩陣的特征值\*39 = 散布矩陣的特征值。 * 當然，我們也可以快速驗證一下特征值-特征向量的計算是否正確，是不是滿足方程（其中為協方差矩陣，v為特征向量，lambda為特征值）。 ``` 1 for i in range(len(eig_val_sc)): 2 eigv = eig_vec_sc[:,i].reshape(1,3).T 3 np.testing.assert_array_almost_equal(scatter_matrix.dot(eigv), eig_val_sc[i] * eigv,decimal=6, err_msg='', verbose=True) ``` * 得出結果未返回異常，證明計算正確 * 注：np.testing.assert_array_almost_equal計算得出的結果不一樣會返回一下結果： ``` >>> np.testing.assert_array_almost_equal([1.0,2.33333,np.nan], ... [1.0,2.33339,np.nan], decimal=5) ... <type 'exceptions.AssertionError'>: AssertionError: Arrays are not almost equal (mismatch 50.0%) x: array([ 1. , 2.33333, NaN]) y: array([ 1. , 2.33339, NaN]) ``` * 可視化特征向量 ``` 1 from matplotlib import pyplot as plt 2 from mpl_toolkits.mplot3d import Axes3D 3 from mpl_toolkits.mplot3d import proj3d 4 from matplotlib.patches import FancyArrowPatch 5 6 7 class Arrow3D(FancyArrowPatch): 8 def __init__(self, xs, ys, zs, *args, **kwargs): 9 FancyArrowPatch.__init__(self, (0,0), (0,0), *args, **kwargs) 10 self._verts3d = xs, ys, zs 11 12 def draw(self, renderer): 13 xs3d, ys3d, zs3d = self._verts3d 14 xs, ys, zs = proj3d.proj_transform(xs3d, ys3d, zs3d, renderer.M) 15 self.set_positions((xs[0],ys[0]),(xs[1],ys[1])) 16 FancyArrowPatch.draw(self, renderer) 17 18 fig = plt.figure(figsize=(7,7)) 19 ax = fig.add_subplot(111, projection='3d') 20 21 ax.plot(all_samples[0,:], all_samples[1,:], all_samples[2,:], 'o', markersize=8, color='green', alpha=0.2) 22 ax.plot([mean_x], [mean_y], [mean_z], 'o', markersize=10, color='red', alpha=0.5) 23 for v in eig_vec_sc.T: 24 a = Arrow3D([mean_x, v[0]], [mean_y, v[1]], [mean_z, v[2]], mutation_scale=20, lw=3, arrowstyle="-|>", color="r") 25 ax.add_artist(a) 26 ax.set_xlabel('x_values') 27 ax.set_ylabel('y_values') 28 ax.set_zlabel('z_values') 29 30 plt.title('Eigenvectors') 31 32 plt.show() ``` * 結果：  ### 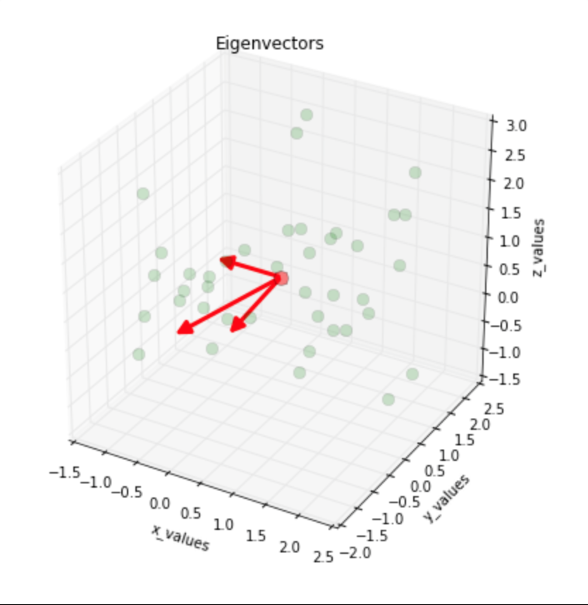7.根據特征值對特征向量降序排列 * ?我們的目標是減少特征空間的維度，即通過PCA方法將特征空間投影到一個小一點的子空間里，其中特征向量將會構成新的特征空間的軸。然而，特征向量只會決定軸的方向，他們的單位長度都為1，可以用代碼檢驗一下： ``` 1 for ev in eig_vec_sc: 2 numpy.testing.assert_array_almost_equal(1.0, np.linalg.norm(ev)) ``` * 因此，對于低維的子空間來說，決定丟掉哪個特征向量，就必須參考特征向量相應的特征值。通俗來說，如果一個特征向量的特征值特別小，那它所包含的數據分布的信息也很少，那么這個特征向量就可以忽略不計了。常用的方法是根據特征值對特征向量進行降序排列，選出前k個特征向量。 ``` # 生成（特征向量，特征值）元祖 eig_pairs = [(np.abs(eig_val_sc[i]), eig_vec_sc[:,i]) for i in range(len(eig_val_sc))] #對（特征向量，特征值）元祖按照降序排列 eig_pairs.sort(key=lambda x: x[0], reverse=True) #輸出值 for i in eig_pairs: print(i[0]) ``` * 結果： ``` 1 84.5729942896 2 39.811391232 3 21.2275760682 ``` ### 8.選出前k個特征值最大的特征向量 * 本文的例子是想把三維的空間降維成二維空間，現在我們把前兩個最大特征值的特征向量組合起來，生成d\*k維的特征向量矩陣W ``` 1 matrix_w = np.hstack((eig_pairs[0][1].reshape(3,1), eig_pairs[1][1].reshape(3,1))) 2 print('Matrix W:\n', matrix_w) ``` * 結果： ``` 1 >>> print('Matrix W:\n', matrix_w) 2 Matrix W:, 3 array([[-0.62497663, 0.2126888 ], 4 [-0.44135959, -0.88989795], 5 [-0.643899 , 0.40354071]])) ``` ### 9.將樣本轉化為新的特征空間 * 最后一步，把2\*3維的特征向量矩陣W帶到公式中，將樣本數據轉化為新的特征空間 ``` 1 matrix_w = np.hstack((eig_pairs[0][1].reshape(3,1), eig_pairs[1][1].reshape(3,1))) 2 print('Matrix W:\n', matrix_w) 3 4 5 transformed = matrix_w.T.dot(all_samples) 6 assert transformed.shape == (2,40), "The matrix is not 2x40 dimensional." 7 8 9 plt.plot(transformed[0,0:20], transformed[1,0:20], 'o', markersize=7, color='blue', alpha=0.5, label='class1') 10 plt.plot(transformed[0,20:40], transformed[1,20:40], '^', markersize=7, color='red', alpha=0.5, label='class2') 11 plt.xlim([-4,4]) 12 plt.ylim([-4,4]) 13 plt.xlabel('x_values') 14 plt.ylabel('y_values') 15 plt.legend() 16 plt.title('Transformed samples with class labels') 17 18 plt.show() ``` * 結果：  * 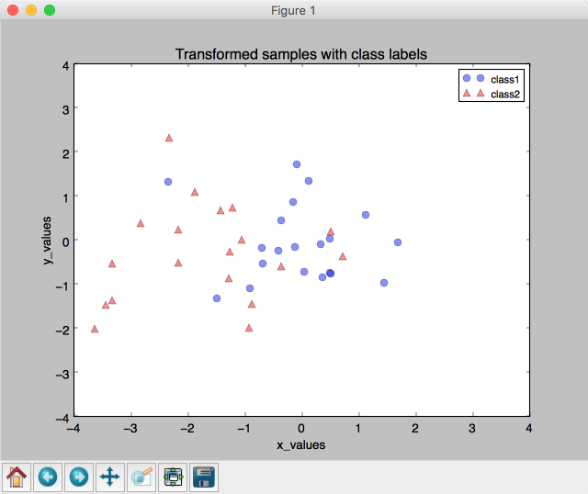到這一步，PCA的過程就結束了。其實python里有已經寫好的模塊，可以直接拿來用，但是我覺得不管什么模塊，都要懂得它的原理是什么。matplotlib有[matplotlib.mlab.PCA()](http://www.cnblogs.com/https:/www.clear.rice.edu/comp130/12spring/pca/pca_docs.shtml)，sklearn也有專門一個模塊[Dimensionality reduction](http://scikit-learn.org/stable/modules/decomposition.html#decompositions)專門講PCA，包括傳統的PCA，也就是我上文寫的，以及增量PCA，核PCA等等，除了PCA以外，還有ZCA白化等等，在圖像處理中也經常會用到。 * 　　最后推薦一個博客，動態展示了PCA的過程：http://setosa.io/ev/principal-component-analysis/ ?寫的也很清楚，可以看一下；再推薦一個維基百科的， https://en.wikipedia.org/wiki/Principal\_component\_analysis