#### 第11章:
#### 數據結構
#### 11.1 什么是數據結構:
1. 數據
2. 數據元素
3. 數據對象
4. 數據結構
##### 數據
對客觀事物的符號表示。在計算機科學中是指所有能輸入到計算機中并被計算機程序處理的符號總稱。對計算機的含義極為廣泛,如圖像、聲音等都可以通過編碼而歸之于數據范疇。
##### 數據元素
數據的基本單位,在計算機程序中通常`作為一個整體`進行考慮和處理。
例如:一本書的書目信息為一個數據元素,而數目中的每一項(書名、作者名等)為一個`數據項`。`數據項是數據的不可分割的最小單位`。
##### 數據對象
`數據對象是性質相同的數據元素的集合`,是數據的一個子集。例如整數的數據對象是A={...,-4,-3,-2,-1,0,1,2,3,4,...},字母字符數據對象是C={A,B,C,D,E,...}。
##### 數據結構
`數據結構是相互之間存在一種或多種特定關系的數據元素的集合`。在任何問題中,數據元素都不是孤立存在的,而是在它們之間存在著某種關系,這種數據元素之間的關系稱為結構。
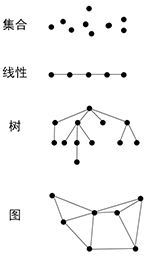
根據數據元素之間關系的不同特性,通常由下列4類基本結構:
1. `集合`
結構中的數據元素之間除了”同屬一個集合“的關系外,別無其他關系。
2. `線性結構`
結構中的數據元素之間存在一個對一個的關系。
3. `樹形結構`
結構中的元素之間存在一個對多個的關系。
4. `圖狀結構`或`網狀結構`
5. 結構中的數據元素之間存在多個對多個的關系。
:-: 
結構定義中的”關系“描述的是數據元素之間的邏輯關系,因此又稱為數據的邏輯結構。
數據結構在計算機中的表示(又稱映像)稱為數據的物理結構,又稱存儲結構。它包括數據元素的表示和關系的表示。
#### 11.2 算法
算法是對特定問題求解步驟的一種描述。它是指令的有限序列,其中每一條指令表示一個或多個操作。此外,一個算法還具有下列5個重要特性:
* 有窮性:一個算法必須總是在執行有窮步之后結束,且每一步都可在有窮時間內完成。
* 確定性:算法中每一條指令必須由確切的含義,讀者理解時不會產生二義性。并且,在任何條件下,算法只有惟一的一條執行路徑,即對于相同的輸入只能得出相同的輸出。
* 可行性:一個算法是能行的,即算法中描述的操作都是可以通過已經實現的基本運算執行有限次來實現的。
* 輸入:一個算法有零個或多個輸入,這些輸入取自于某個特定的對象的集合。
* 輸出:一個算法有一個或多個輸出,這些輸出是同輸入有著某些特定關系的量。
##### 算法的設計要求
通常設計一個”好“的算法應該考量達到以下目標。
1. 正確性:算法應當滿足具體問題的需求。正確一詞分為4個層次,a.程序不含語法錯誤;b.程序對于幾組輸入數據能夠得出滿足規格說明要求的結果;c.程序對于精心選擇的典型、苛刻而帶有刁難性的幾組輸入數據能夠得出滿足規格說明要求的結果;d.程序對于一切合法的輸入數據都能產生滿足規格說明要求的結果。
2. 可讀性:算法主要是為了人的閱讀于交流,其次才是機器執行。可讀性有助于人對算法的理解;晦澀難懂的程序易于隱藏較多錯誤,難以調試和修改。
3. 健壯性:當輸入數據非法時,算法也能適當地做出反應或進行處理,而不是產生莫名奇妙地輸出結果。
4. 效率與低儲量需求:通俗地說,效率指的是算法的執行的時間。對于同一個問題如果有多個算法可以解決,執行時間短的算法效率高。存儲量需求指算法執行過程中所需要的最大存儲空間。效率與低存儲量需求這兩者都與問題的規模有關。
##### 算法的度量
1)事后統計的方法。
不做描述
2)事前分析估算的方法。
1. 依據算法選用何種策略。
2. 問題的規模,例如求100以內還是1000以內的素數。
3. 書寫程序的語言,對于同一個算法,實現語言的級別越高,執行效率越低。
4. 編譯程序所產生的機器代碼的質量。
5. 機器執行指令的速度。
##### 算法的時間復雜度
一般情況,算法中基本操作重復執行的次數是問題規模n的某個函數f(n),算法的時間量度記作
**T(n)=O(f(n))**
它表示隨問題規模n的增大,算法執行時間的增長率和f(n)的增長率相同,也叫做算法的`漸進時間復雜度`,簡稱時間復雜度。
語句的`頻度`指的是該語句重復執行的次數。也就是原操作執行的次數。
(a)
~~~
{++x;s = 0}
~~~
(b)
~~~
for(i = 1;i<=n;++i){++x;s += x;}
~~~
(c)
~~~
for(j = 1; j<=n;++j)
for(k = 1;k<=n;++k){++x;s += x;}
~~~
以上三個程序中,含基本操作”x增1“的語句頻度分別為1、n和n的2次方。則這三個程序段的時間復雜度分別為O(1),O(n),O(n的二次方)。分別稱為`常量階`、`線性階`、`平方階`。算法還能呈現的時間復雜度有`對數階O(logn)`、`指數階O(2的n次方)`。應該盡可能地選擇`多項階式O(n的k次方)`,而不希望用指數階的算法。
##### 算法的空間復雜度
空間復雜度作為算法所需存儲空間按的度量。
**S(n)=O(f(n))**
其中n為問題的規模(大小)。一個上機執行的程序除了需要存儲空間來寄存本身所用的指令、常數、變量、和輸入數據外,也需要一些對數據進行操作的工作單元和存儲一些為實現所需信息的輔助空間。
#### 11.3 線性表
線性結構的特點是:在數據元素的非空有限集合中,(1)存在惟一的一個被稱作”第一個“的數據元素(2)存在惟一的一個被稱為”最后一個“的數據元素;(3)除第一個之外,集合中的每個數據元素均只有一個前驅;(4)除最后一個之外,集合中每個數據元素均只有一個后繼。
**線性表**是最常用且最簡單的一種數據結構。一個線性表是n個數據元素的有限序列。
例如:
26個英文字母的字母表:(A,B,C,···,Z)
某校從1976年到1983年各種類型計算機擁有量的變化情況:(6,17,28,50,92,188)
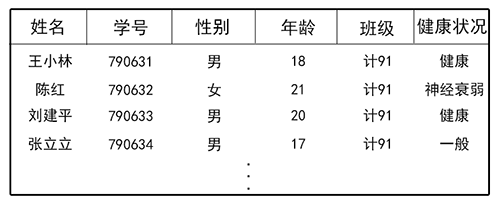
稍復雜的線性表中,一個數據元素可以由若干個`數據項`組成。在這種情況下,常把元素稱為`記錄`,含有大量記錄的線性表又稱為`文件`。
例如,一個學校的學生健康情況登記表,其中每個學生的情況為一個記錄(一條數據元素由多條數據項組成)。它由姓名、學號、性別、年齡、班級、和健康等數據項組成。
:-: 
##### 線性表的順序表現和實現
連續的存儲單元:
線性表的順序表示指的是用一組地址連續的存儲單元順序地存儲線性表的數據元素。
##### 線性表的鏈式表示和實現
線性鏈表:
線性表的鏈式存儲結構的特點是用一組任意的存儲單元存儲線性表的數據元素(這組存儲單元物理上可以是連續的,也可以是不連續的)。因此,為了表示每個數據元素a(i)與其a(i+1)之間的邏輯關系,對數據元素a(i)來說,除了存儲本身的信息之外,還需要存儲一個指向其直接后繼的信息(即直接后繼的存儲位置),就要用到指針。這兩部分組成了a(i)的存儲映像,稱為結點。這個結點包括兩個域:`數據域`和`指針域`。
:-: 
##### 循環鏈表
循環鏈表最后結點的指針域指向頭部結點。
##### 雙向鏈表
雙向鏈表有兩個指針域,頭指針域指向前一個結點,尾指針域指向下一個結點
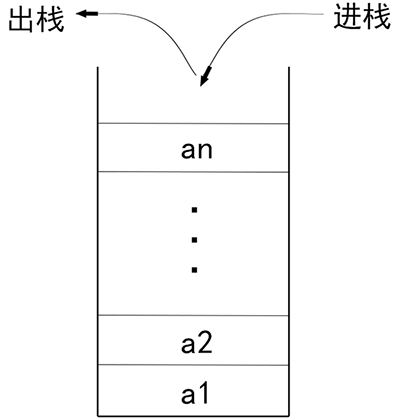
##### 棧
棧是計算機程序中非常重要的一種簡單的線性結構。是一種先進后出的結構。
:-: 
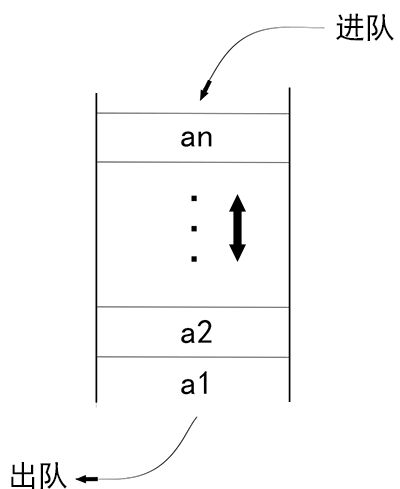
##### 隊列
和棧相反,隊列是先進先出。
:-: 
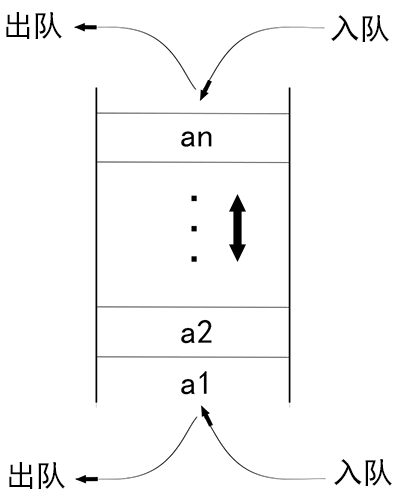
`雙端隊列`是一種限定插入和刪除操作在表的兩端進行的線性表。
:-: 
##### 循環隊列
有興趣的可以自己去查閱資料。
##### 串
串是由零個或多個字符組成的。
a=“BEI”;
b=“JING”;
c=“BEIJING”;
d=“BEI JING”;
#### 11.4 數組和廣義表
前面講的線性結構中的數據元素都是非結構性的原子類型,元素的值是不再分割的。
數組和廣義表可以看成是線性表在此述含義中的擴展:表中的數據元素本身是一個數據結構。
:-: 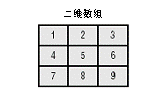
二維數組
:-: 
廣義表
#### 11.5 樹和二叉樹
樹形結構是一類重要的非線性數據結構。常用于數據庫系統。其中樹和二叉樹最為常用,直觀來看樹是以分支關系定義的層次結構。樹結構在客觀世界中廣泛存在,如人類社會的族譜和各種社會組織機構都可用樹來形象表示。
關于樹的概念:
1. 度:樹的層次
2. 根:樹最初的結點
3. 雙親和孩子:結點的子樹根稱為該結點的孩子。相應的,該結點稱為孩子的雙親。
4. 祖先和子孫:以某結點為根的子樹中的任一結點都稱為該結點的子孫。反之,祖先是從根結點到該結點所經分支上的所有結點。
5. 葉子:沒有子孫的結點。
:-: 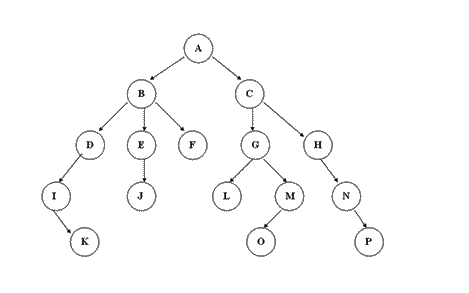
樹
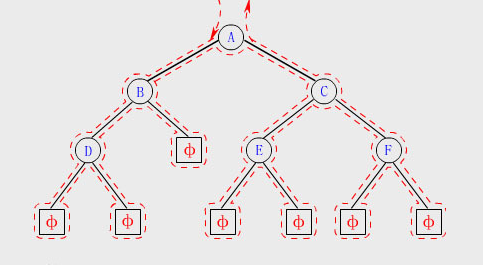
##### 樹
樹:
是n(n>=0)個結點的有限集。在任意一個非空樹中:
1. 有且僅有一個特定的稱為根的結點;(上圖的A結點)
2. 當n>1時,其余結點可分為m(m>0)個互不相交的有限集T1,T2,T3 ····,其中每個集合本身又是一棵樹,并且稱為根的`子樹`。
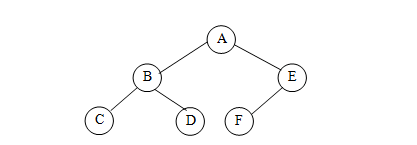
二叉樹:
是另一種樹型結構,它的特點是每個結點至多只有兩顆子樹。并且,二叉樹的子樹有左右之分,其次序不能任意顛倒。意思是在數據存儲時應該遵循從左向右的原則。
:-: 
完全二叉樹:
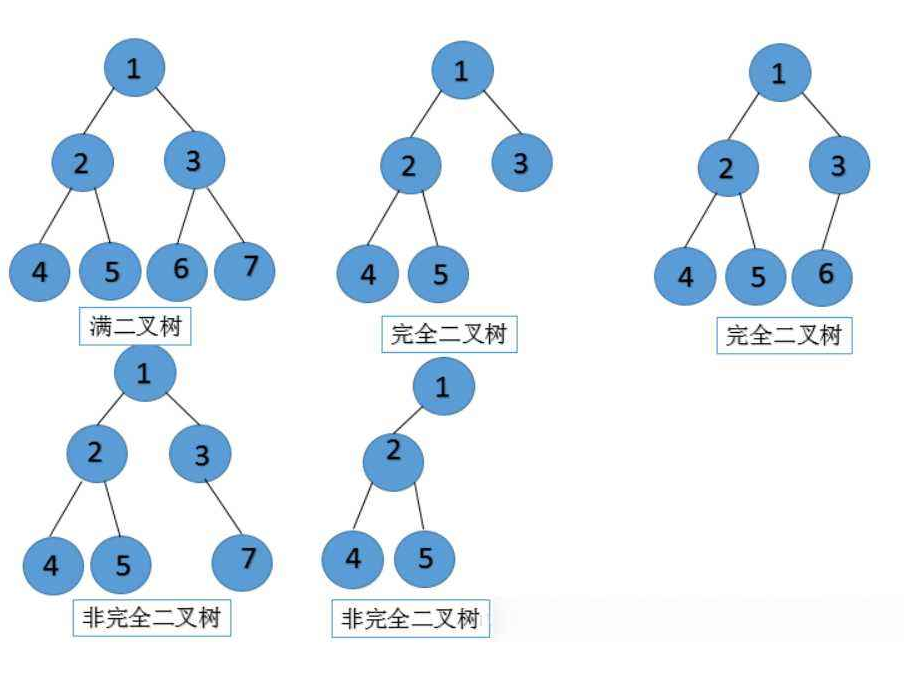
一棵深度為k的有n個結點的二叉樹,對樹中的結點按從上至下、從左到右的順序進行編號,如果編號為i(1≤i≤n)的結點與滿二叉樹中編號為i的結點在二叉樹中的位置相同,則這棵二叉樹稱為完全二叉樹(比如滿二叉樹5和完全二叉樹5的節點位置一樣,其他的1234也都一樣,就是完全二叉樹。)。
:-: 
完全二叉樹的結點數據存儲表示(完全二叉樹遵循從上到下從左到右原則)
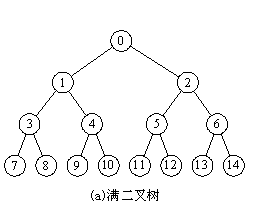
滿二叉樹:
:-: 
區別示意圖:
:-: 
遍歷二叉樹:
:-: