# 7.7 AdaDelta算法 除了RMSProp算法以外，另一個常用優化算法AdaDelta算法也針對AdaGrad算法在迭代后期可能較難找到有用解的問題做了改進 [1]。有意思的是，**AdaDelta算法沒有學習率這一超參數**。 ## 7.7.1 算法 AdaDelta算法也像RMSProp算法一樣，使用了小批量隨機梯度`$ \boldsymbol{g}_t $`按元素平方的指數加權移動平均變量`$ \boldsymbol{s}_t $`。在時間步0，它的所有元素被初始化為0。給定超參數`$ 0 \leq \rho < 1 $`（對應RMSProp算法中的 `$ \gamma $`），在時間步`$ t>0 $`，同RMSProp算法一樣計算 ```[tex] \boldsymbol{s}_t \leftarrow \rho \boldsymbol{s}_{t-1} + (1 - \rho) \boldsymbol{g}_t \odot \boldsymbol{g}_t. ``` 與RMSProp算法不同的是，AdaDelta算法還維護一個額外的狀態變量`$ \Delta\boldsymbol{x}_t $`，其元素同樣在時間步0時被初始化為0。我們使用`$ \Delta\boldsymbol{x}_{t-1} $`來計算自變量的變化量： ```[tex] \boldsymbol{g}_t' \leftarrow \sqrt{\frac{\Delta\boldsymbol{x}_{t-1} + \epsilon}{\boldsymbol{s}_t + \epsilon}} \odot \boldsymbol{g}_t, ``` 其中`$ \epsilon $`是為了維持數值穩定性而添加的常數，如`$ 10^{-5} $` 。接著更新自變量： ```[tex] \boldsymbol{x}_t \leftarrow \boldsymbol{x}_{t-1} - \boldsymbol{g}'_t. ``` 最后，我們使用`$ \Delta\boldsymbol{x}_t $`來記錄自變量變化量`$ \boldsymbol{g}'_t $`按元素平方的指數加權移動平均： ```[tex] \Delta\boldsymbol{x}_t \leftarrow \rho \Delta\boldsymbol{x}_{t-1} + (1 - \rho) \boldsymbol{g}'_t \odot \boldsymbol{g}'_t. ``` 可以看到，如不考慮`$ \epsilon $`的影響，**AdaDelta算法跟RMSProp算法的不同之處在于使用`$ \sqrt{\Delta\boldsymbol{x}_{t-1}} $`來替代學習率`$ \eta $`**。 ## 7.7.2 從零開始實現 AdaDelta算法需要對每個自變量維護兩個狀態變量，即`$ \boldsymbol{s}_t $`和`$ \Delta\boldsymbol{x}_t $`。我們按AdaDelta算法中的公式實現該算法。 ``` python %matplotlib inline import torch import sys sys.path.append("..") import d2lzh_pytorch as d2l features, labels = d2l.get_data_ch7() def init_adadelta_states(): s_w, s_b = torch.zeros((features.shape[1], 1), dtype=torch.float32), torch.zeros(1, dtype=torch.float32) delta_w, delta_b = torch.zeros((features.shape[1], 1), dtype=torch.float32), torch.zeros(1, dtype=torch.float32) return ((s_w, delta_w), (s_b, delta_b)) def adadelta(params, states, hyperparams): rho, eps = hyperparams['rho'], 1e-5 for p, (s, delta) in zip(params, states): s[:] = rho * s + (1 - rho) * (p.grad.data**2) g = p.grad.data * torch.sqrt((delta + eps) / (s + eps)) p.data -= g delta[:] = rho * delta + (1 - rho) * g * g ``` 使用超參數$\rho=0.9$來訓練模型。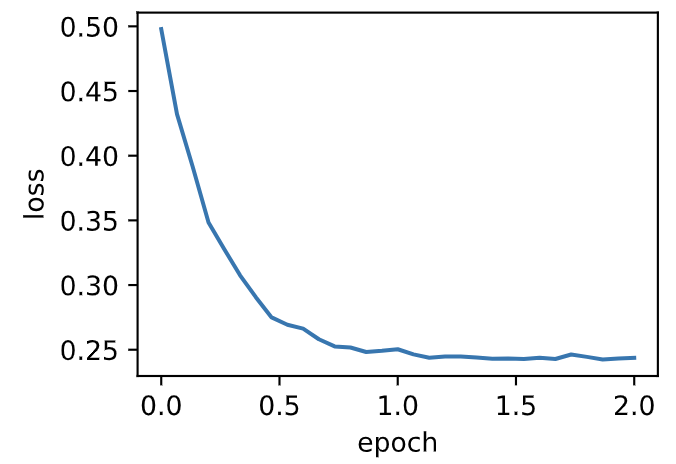 ``` python d2l.train_ch7(adadelta, init_adadelta_states(), {'rho': 0.9}, features, labels) ``` 輸出： ``` loss: 0.243728, 0.062991 sec per epoch ``` :-:  ## 7.7.3 簡潔實現 通過名稱為`Adadelta`的優化器方法，我們便可使用PyTorch提供的AdaDelta算法。它的超參數可以通過`rho`來指定。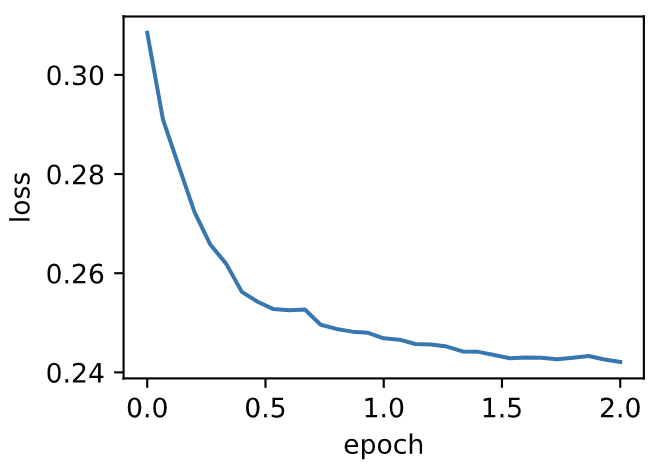 ``` python d2l.train_pytorch_ch7(torch.optim.Adadelta, {'rho': 0.9}, features, labels) ``` 輸出： ``` loss: 0.242104, 0.047702 sec per epoch ``` :-:  ## 小結 * AdaDelta算法沒有學習率超參數，它通過使用有關自變量更新量平方的指數加權移動平均的項來替代RMSProp算法中的學習率。 ## 參考文獻 [1] Zeiler, M. D. (2012). ADADELTA: an adaptive learning rate method. arXiv preprint arXiv:1212.5701. ----------- > 注：除代碼外本節與原書此節基本相同，[原書傳送門](https://zh.d2l.ai/chapter_optimization/adadelta.html)