# 四、數據類型 > 原文：[Data Types](https://github.com/data-8/textbook/tree/gh-pages/chapters/04) > 譯者：[飛龍](https://github.com/wizardforcel) > 協議：[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 每個值都有一個類型，內建的`type`函數返回任何表達式的結果的類型： ```py type(3) int type(3/1) float ``` 表達式的`type`是其最終值的類型。 所以，`type`函數永遠不會表明，表達式的類型是一個名稱，因為名稱總是求值為它們被賦予的值。 ```py x = 3 type(x) # The type of x is an int, not a name int ``` 我們已經遇到的另一種類型是內置函數。 Python 表明這個類型是一個`builtin_function_or_method`；函數和方法之間的區別在這個階段并不重要。 ```py type(abs) builtin_function_or_method ``` 這一章會探索其他實用的數據類型。 ## 字符串 世界上大部分的數據都是文本，計算機中表示的文本被稱為字符串。 字符串可以代表一個單詞，一個句子，甚至是圖書館中每本書的內容。 由于文本可以包含數字（如`5`）或布爾值（`True`），字符串也可以描述這些東西。 表達式的含義取決于其結構和正在組合的值的類型。 因此，例如，將兩個字符串加在一起會產生另一個字符串。 這個表達式仍然是一個加法表達式，但是它組合了一個不同類型的值。 ```py "data" + "science" 'datascience' ``` 加法完全是字面的；它將這兩個字符串組合在一起而不考慮其內容。 它不增加空間，因為這些是不同的詞；它取決于程序員（你）來指定。 ```py "data" + " " + "science" 'data science' ``` 單引號和雙引號都可以用來創建字符串：`'hi'`和`"hi"`是相同的表達式。 雙引號通常是首選，因為它們允許在字符串中包含單引號。 ```py "This won't work with a single-quoted string!" "This won't work with a single-quoted string!" ``` 為什么不能？ 試試看。 `str`函數返回任何值的字符串表示形式。 使用此函數，可以構建具有嵌入值的字符串。 ```py "That's " + str(1 + 1) + ' ' + str(True) "That's 2 True" ``` ## 字符串方法 可以使用字符串方法，從現有的字符串中構造相關的字符串，這些方法是操作字符串的函數。 這些方法通過在字符串后面放置一個點，然后調用該函數來調用。 例如，以下方法生成一個字符串的大寫版本。 ```py "loud".upper() 'LOUD' ``` 也許最重要的方法是`replace`，它替換字符串中的所有子字符串的實例。 `replace`方法有兩個參數，即被替換的文本和替代值。 ```py 'hitchhiker'.replace('hi', 'ma') 'matchmaker' ``` 字符串方法也可以使用變量名稱進行調用，只要這些名稱綁定到字符串。 因此，例如，通過首先創建`"ingrain" `然后進行第二次替換，以下兩個步驟的過程從`"train"`生成`"degrade"`一詞。 ```py s = "train" t = s.replace('t', 'ing') u = t.replace('in', 'de') u 'degrade' ``` 注意`t = s.replace('t', 'ing')`的一行，不改變字符串`s`，它仍然是`"train"`。 方法調用`s.replace('t', 'ing')`只有一個值，即字符串`"ingrain"`。 ```py s 'train' ``` 這是我們第一次看到方法，但是方法并不是字符串僅有的。 我們將很快看到，其他類型的對象可以擁有它們。 ## 比較 布爾值通常來自比較運算符。 Python 包含了各種比較值的運算符。 例如，`3 > 1 + 1`。 ```py 3 > 1 + 1 True ``` 值`True`表明這個比較是有效的；Python 已經證實了`3`和`1 + 1`之間關系的這個簡單的事實。下面列出了一整套通用的比較運算符。 | 比較 | 運算符 | True 示例 | False 示例 | | --- | --- | --- | --- | | 小于 | `<` | `2 < 3` | `2 < 2` | | 大于 | `>` | `3 > 2` | `3 > 3` | | 小于等于 | `<=` | `2 <= 2` | `3 <= 2` | | 大于等于 | `>=` | `3 >= 3` | `2 >= 3` | | 等于 | `==` | `3 == 3` | `3 == 2` | | 不等于 | `!=` | `3 != 2` | `2 != 2` | 一個表達式可以包含多個比較，并且為了使整個表達式為真，它們都必須有效。 例如，我們可以用下面的表達式表示`1 + 1`在`1`和`3`之間。 ```py 1 < 1 + 1 < 3 True ``` 兩個數字的平均值總是在較小的數字和較大的數字之間。 我們用下面的數字`x`和`y`來表示這種關系。 你可以嘗試不同的`x`和`y`值來確認這種關系。 ```py x = 12 y = 5 min(x, y) <= (x+y)/2 <= max(x, y) True ``` 字符串也可以比較，他們的順序是字典序。 較短的字符串小于以較短的字符串開頭的較長的字符串。 ```py "Dog" > "Catastrophe" > "Cat" True ``` ## 序列 值可以分組到集合中，這允許程序員組織這些值，并使用單個名稱引用它們中的所有值。 通過將值分組在一起，我們可以編寫代碼，一次執行許多數據計算。 在幾個值上調用`make_array`函數，將它們放到一個數組中，這是一種順序集合。 下面，我們將四個不同的溫度收集到一個名為`temps`的數組中。 這些分別是 1850 年，1900 年，1950 年和 2000 年的幾十年間，地球上所有陸地的估計日平均絕對高溫（攝氏度），表示為 1951 年至 1980 年間平均絕對高溫的偏差，為 14.48 度。 集合允許我們使用單個名稱，將多個值傳遞給一個函數。 例如，`sum`函數計算集合中所有值的和，`len`函數計算其長度。 （這是我們放入的值的數量。）一起使用它們，我們可以計算一個集合的平均值。 ```py sum(highs)/len(highs) 14.434000000000001 ``` 日高溫和低溫的完整圖表在下面。 ### 日高溫均值  ### 日低溫均值  ## 數組 Python 中有很多種類的集合，我們在這門課中主要使用數組。 我們已經看到，`make_array`函數可以用來創建數值的數組。 數組也可以包含字符串或其他類型的值，但是單個數組只能包含單一類型的數據。 （無論如何，把不相似的數據組合在一起，通常都沒有意義）。例如： ```py english_parts_of_speech = make_array("noun", "pronoun", "verb", "adverb", "adjective", "conjunction", "preposition", "interjection") english_parts_of_speech array(['noun', 'pronoun', 'verb', 'adverb', 'adjective', 'conjunction', 'preposition', 'interjection'], dtype='<U12') ``` > 譯者注： > ```py > import numpy as np > make_array = lambda *args: np.asarray(args) > ``` 返回到溫度數據，我們創建 1850 年，1900 年，1950 年和 2000 年的幾十年間，[日平均高溫](http://berkeleyearth.lbl.gov/auto/Regional/TMAX/Text/global-land-TMAX-Trend.txt)的數組。 ```py baseline_high = 14.48 highs = make_array(baseline_high - 0.880, baseline_high - 0.093, baseline_high + 0.105, baseline_high + 0.684) highs array([ 13.6 , 14.387, 14.585, 15.164]) ``` 數組可以用在算術表達式中來計算其內容。 當數組與單個數組合時，該數與數組的每個元素組合。 因此，我們可以通過編寫熟悉的轉換公式，將所有這些溫度轉換成華氏溫度。 ```py (9/5) * highs + 32 array([ 56.48 , 57.8966, 58.253 , 59.2952]) ```  數組也有方法，這些方法是操作數組值的函數。 數值集合的均值是其總和除以長度。 以下示例中的每對括號都是調用表達式的一部分；它調用一個無參函數來對數組`highs`進行計算。 ```py highs.size 4 highs.sum() 57.736000000000004 highs.mean() 14.434000000000001 ``` ### 數組上的函數 `numpy`包，在程序中縮寫為`np`，為 Python 程序員提供了創建和操作數組的，方便而強大的函數。 ```py import numpy as np ``` 例如，`diff`函數計算數組中每兩個相鄰元素之間的差。 差數組的第一個元素是原數組的第二個元素減去第一個元素。 ```py np.diff(highs) array([ 0.787, 0.198, 0.579]) ``` [完整的 Numpy 參考](http://docs.scipy.org/doc/numpy/reference/)詳細列出了這些功能，但一個小的子集通常用于數據處理應用。 它們分組到了`np`中不同的包中。 學習這些詞匯是學習 Python 語言的重要組成部分，因此在你處理示例和問題時，請經常回顧這個列表。 但是，你不需要記住這些，只需要將它用作參考。 每個這些函數接受數組作為參數，并返回單個值。 | 函數 | 描述 | | --- | --- | | `np.prod` | 將所有元素相乘 | | `np.sum` | 將所有元素相加 | | `np.all` | 測試是否所有元素是真值 （非零數值是真值） | | `np.any` | 測試是否任意元素是真值（非零數值是真值） | | `np.count_nonzero` | 計算非零元素的數量 | 每個這些函數接受字符串數組作為參數，并返回數組。 | 函數 | 描述 | | --- | --- | | `np.char.lower` | 將每個元素變成小寫 | | `np.char.upper` | 將每個元素變成大寫 | | `np.char.strip` | 移除每個元素開頭或末尾的空格 | | `np.char.isalpha` | 每個元素是否只含有字母（沒有數字或者符號） | | `np.char.isnumeric` | 每個元素是否只含有數字（沒有字母） | 每個這些函數接受字符串數組和一個搜索字符串。 | 函數 | 描述 | | --- | --- | | np.char.count | 在數組的元素中，計算搜索字符串的出現次數 | | np.char.find | 在每個元素中，搜索字符串的首次出現位置 | | np.char.rfind | 在每個元素中，搜索字符串的最后一次出現位置 | | np.char.startswith | 每個字符串是否以搜索字符串起始 | ## 范圍 范圍是一個數組，按照遞增或遞減的順序排列，每個元素按照一定的間隔分開。 范圍在很多情況下非常有用，所以值得了解它們。 范圍使用`np.arange`函數來定義，該函數接受一個，兩個或三個參數：起始值，終止值和“步長”。 如果將一個參數傳遞給`np.arange`，那么它將成為終止值，其中`start = 0`，`step = 1`。 兩個參數提供了起始值和終止值，`step = 1`。 三個參數明確地提供了起始值，終止值和步長。 范圍始終包含其`start`值，但不包括其`end`值。 它按照`step`計數，并在到達`end`之前停止。 ```py np.arange(end): An array starting with 0 of increasing consecutive integers, stopping before end. np.arange(5) array([0, 1, 2, 3, 4]) ``` 要注意，數值從`0`起始，并僅僅增加到`4`，并不是`5`。 ```py np.arange(start, end): An array of consecutive increasing integers from start, stopping before end. np.arange(3, 9) array([3, 4, 5, 6, 7, 8]) np.arange(start, end, step): A range with a difference of step between each pair of consecutive values, starting from start and stopping before end. np.arange(3, 30, 5) array([ 3, 8, 13, 18, 23, 28]) ``` 這個數組從`3`起始，增加了步長`5`變成`8`，然后增加步長`5`變成`13`，以此類推。 當你指定步長時，起始值、終止值和步長可正可負，可以是整數也可以是分數。 ```py np.arange(1.5, -2, -0.5) array([ 1.5, 1. , 0.5, 0. , -0.5, -1. , -1.5]) ``` ### 示例：萊布尼茨的 π 公式 偉大的德國數學家和哲學家戈特弗里德·威廉·萊布尼茨（Gottfried Wilhelm Leibniz，1646 ~ 1716年）發現了一個簡單分數的無窮和。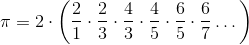 公式是：  雖然需要一些數學來確定它，但我們可以用數組來說服我們自己，公式是有效的。 讓我們計算萊布尼茨的無窮和的前 5000 個項，看它是否接近 π。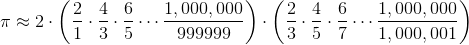 我們將計算這個有限的總和，首先加上所有的正項，然后減去所有負項的和 [1]：  > [1] 令人驚訝的是，當我們將無限多個分數相加時，順序可能很重要。但是我們對 π 的近似只使用了大量的數量有限的分數，所以可以按照任何方便的順序，將這些項相加。 和中的正項的分母是`1, 5, 9`，以此類推。數組`by_four_to_20`包含`17`之前的這些數。 ```py by_four_to_20 = np.arange(1, 20, 4) by_four_to_20 array([ 1, 5, 9, 13, 17]) ``` 為了獲得 π 的準確近似，我們使用更長的數組`positive_term_denominators`。 ```py positive_term_denominators = np.arange(1, 10000, 4) positive_term_denominators array([ 1, 5, 9, ..., 9989, 9993, 9997]) ``` 我們實際打算加起來的正項，就是一除以這些分母。 ```py positive_terms = 1 / positive_term_denominators ``` 負向的分母是`3, 7, 11`，以此類推。這個數組就是`positive_term_denominators`加二。 ```py negative_terms = 1 / (positive_term_denominators + 2) ``` 整體的和是： ```py 4 * ( sum(positive_terms) - sum(negative_terms) ) 3.1413926535917955 ``` 這非常接近于`π = 3.14159...`。萊布尼茨公式看起來不錯。