# 十五、分類
> 原文:[Classification](https://github.com/data-8/textbook/tree/gh-pages/chapters/15)
> 譯者:[飛龍](https://github.com/wizardforcel)
> 協議:[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/)
> 自豪地采用[谷歌翻譯](https://translate.google.cn/)
[David Wagner](https://en.wikipedia.org/wiki/David_A._Wagner) 是這一章的主要作者。
機器學習是一類技術,用于自動尋找數據中的規律,并使用它來推斷或預測。你已經看到了線性回歸,這是一種機器學習技術。本章介紹一個新的技術:分類。
分類就是學習如何根據過去的例子做出預測。我們舉了一些例子,告訴我們什么是正確的預測,我們希望從這些例子中學習,如何較好地預測未來。以下是在實踐中分類的一些應用領域:
+ 他們有一些每個訂單的信息(例如,它的總值,訂單是否被運送到這個客戶以前使用過的地址,是否與信用卡持有人的賬單地址相同)。他們有很多過去的訂單數據,他們知道哪些過去的訂單是欺詐性的,哪些不是。他們想要學習規律,這將幫助他們預測新訂單到達時,這些新訂單是否有欺詐行為。
+ 在線約會網站希望預測:這兩個人合適嗎?他們有很多數據,他們過去向顧客推薦一些東西,它們就知道了哪個是成功的。當新客戶注冊時,他們想預測誰可能是他們的最佳伴侶。
+ 醫生想知道:這個病人是否患有癌癥?根據一些實驗室測試的結果,他們希望能夠預測特定患者是否患有癌癥。基于一些實驗室測試的測量結果,以及他們是否最終發展成癌癥,并且由此他們希望嘗試推斷,哪些測量結果傾向于癌癥(或非癌癥)特征,以便能夠準確地診斷未來的患者。
+ 政客們想預測:你打算為他們投票嗎?這將幫助他們將籌款工作集中在可能支持他們的人身上,并將動員工作集中在投票給他們的人身上。公共數據庫和商業數據庫有大多數人的大量信息,例如,他們是否擁有房屋或房租;他們是否住在富裕的社區還是貧窮的社區;他們的興趣和愛好;他們的購物習慣;等等。政治團體已經調查了一些選民,并找到了他們計劃投票的人,所以他們有一些正確答案已知的例子。
所有這些都是分類任務。請注意,在每個例子中,預測是一個是與否的問題 - 我們稱之為二元分類,因為只有兩個可能的預測。
在分類任務中,我們想要進行預測的每個個體或情況都稱為觀測值。我們通常有很多觀測值。每個觀測值具有多個已知屬性(例如,亞馬遜訂單的總值,或者選民的年薪)。另外,每個觀測值都有一個類別,這是對我們關心的問題(例如欺騙與否,或者是否投票)的回答。
當亞馬遜預測訂單是否具有欺詐性時,每個訂單都對應一個單獨的觀測值。每個觀測值都有幾個屬性:訂單的總值,訂單是否被運送到此客戶以前使用的地址等等。觀測值類別為 0 或 1,其中 0 意味著訂單不是欺詐,1 意味著訂單是欺詐性的。當一個客戶生成新的訂單時,我們并沒有觀察到這個訂單是否具有欺詐性,但是我們確實觀察了這個訂單的屬性,并且我們會嘗試用這些屬性來預測它的類別。
分類需要數據。它涉及到發現規律,并且為了發現規律,你需要數據。這就是數據科學的來源。特別是,我們假設我們可以獲得訓練數據:一系列的觀測數據,我們知道每個觀測值的類別。這些預分類的觀測值集合也被稱為訓練集。分類算法需要分析訓練集,然后提出一個分類器:用于預測未來觀測值類別的算法。
分類器不需要是完全有用的。即使準確度低于 100%,它們也可以是有用的。例如,如果在線約會網站偶爾會提出不好的建議,那沒關系;他們的顧客已經預期,在他們找到真愛之前需要遇見許多人。當然,你不希望分類器犯太多的錯誤,但是不必每次都得到正確的答案。
## 最近鄰
在本節中,我們將開發最近鄰分類方法。 如果一些代碼神秘,不要擔心,現在只要把注意力思路上。 在本章的后面,我們將看到如何將我們的想法組織成執行分類的代碼。
### 慢性腎病
我們來瀏覽一個例子。 我們將使用收集的數據集來幫助醫生診斷慢性腎病(CKD)。 數據集中的每一行都代表單個患者,過去接受過治療并且診斷已知。 對于每個患者,我們都有一組血液測試的測量結果。 我們希望找到哪些測量結果對診斷慢性腎病最有用,并根據他們的血液檢查結果,開發一種方法,將未來的患者分類為“CKD”或“非 CKD”。
```py
ckd = Table.read_table('ckd.csv').relabeled('Blood Glucose Random', 'Glucose')
ckd
```
| Age | Blood Pressure | Specific Gravity | Albumin | Sugar | Red Blood Cells | Pus Cell | Pus Cell clumps | Bacteria | Glucose | Blood Urea | Serum Creatinine | Sodium | Potassium | Hemoglobin | Packed Cell Volume | White Blood Cell Count | Red Blood Cell Count | Hypertension | Diabetes Mellitus | Coronary Artery Disease | Appetite | Pedal Edema | Anemia | Class |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 48 | 70 | 1.005 | 4 | 0 | normal | abnormal | present | notpresent | 117 | 56 | 3.8 | 111 | 2.5 | 11.2 | 32 | 6700 | 3.9 | yes | no | no | poor | yes | yes | 1 |
| 53 | 90 | 1.02 | 2 | 0 | abnormal | abnormal | present | notpresent | 70 | 107 | 7.2 | 114 | 3.7 | 9.5 | 29 | 12100 | 3.7 | yes | yes | no | poor | no | yes | 1 |
| 63 | 70 | 1.01 | 3 | 0 | abnormal | abnormal | present | notpresent | 380 | 60 | 2.7 | 131 | 4.2 | 10.8 | 32 | 4500 | 3.8 | yes | yes | no | poor | yes | no | 1 |
| 68 | 80 | 1.01 | 3 | 2 | normal | abnormal | present | present | 157 | 90 | 4.1 | 130 | 6.4 | 5.6 | 16 | 11000 | 2.6 | yes | yes | yes | poor | yes | no | 1 |
| 61 | 80 | 1.015 | 2 | 0 | abnormal | abnormal | notpresent | notpresent | 173 | 148 | 3.9 | 135 | 5.2 | 7.7 | 24 | 9200 | 3.2 | yes | yes | yes | poor | yes | yes | 1 |
| 48 | 80 | 1.025 | 4 | 0 | normal | abnormal | notpresent | notpresent | 95 | 163 | 7.7 | 136 | 3.8 | 9.8 | 32 | 6900 | 3.4 | yes | no | no | good | no | yes | 1 |
| 69 | 70 | 1.01 | 3 | 4 | normal | abnormal | notpresent | notpresent | 264 | 87 | 2.7 | 130 | 4 | 12.5 | 37 | 9600 | 4.1 | yes | yes | yes | good | yes | no | 1 |
| 73 | 70 | 1.005 | 0 | 0 | normal | normal | notpresent | notpresent | 70 | 32 | 0.9 | 125 | 4 | 10 | 29 | 18900 | 3.5 | yes | yes | no | good | yes | no | 1 |
| 73 | 80 | 1.02 | 2 | 0 | abnormal | abnormal | notpresent | notpresent | 253 | 142 | 4.6 | 138 | 5.8 | 10.5 | 33 | 7200 | 4.3 | yes | yes | yes | good | no | no | 1 |
| 46 | 60 | 1.01 | 1 | 0 | normal | normal | notpresent | notpresent | 163 | 92 | 3.3 | 141 | 4 | 9.8 | 28 | 14600 | 3.2 | yes | yes | no | good | no | no | 1 |
(省略了 148 行)
一些變量是類別(像“異常”這樣的詞),還有一些是定量的。 定量變量都有不同的規模。 我們將要通過眼睛比較和估計距離,所以我們只選擇一些變量并在標準單位下工作。 之后我們就不用擔心每個變量的規模。
```py
ckd = Table().with_columns(
'Hemoglobin', standard_units(ckd.column('Hemoglobin')),
'Glucose', standard_units(ckd.column('Glucose')),
'White Blood Cell Count', standard_units(ckd.column('White Blood Cell Count')),
'Class', ckd.column('Class')
)
ckd
```
| Hemoglobin | Glucose | White Blood Cell Count | Class |
| --- | --- | --- | --- |
| -0.865744 | -0.221549 | -0.569768 | 1 |
| -1.45745 | -0.947597 | 1.16268 | 1 |
| -1.00497 | 3.84123 | -1.27558 | 1 |
| -2.81488 | 0.396364 | 0.809777 | 1 |
| -2.08395 | 0.643529 | 0.232293 | 1 |
| -1.35303 | -0.561402 | -0.505603 | 1 |
| -0.413266 | 2.04928 | 0.360623 | 1 |
| -1.28342 | -0.947597 | 3.34429 | 1 |
| -1.10939 | 1.87936 | -0.409356 | 1 |
| -1.35303 | 0.489051 | 1.96475 | 1 |
(省略了 148 行)
我們來看兩列,(病人的血液中)血紅蛋白水平和血糖水平(一天中的隨機時間;沒有專門為血液測試禁食)。
我們將繪制一個散點圖來顯示兩個變量之間的關系。 藍點是 CKD 患者; 金點是非 CKD 的患者。 什么樣的醫學檢驗結果似乎表明了 CKD?
```py
color_table = Table().with_columns(
'Class', make_array(1, 0),
'Color', make_array('darkblue', 'gold')
)
ckd = ckd.join('Class', color_table)
ckd.scatter('Hemoglobin', 'Glucose', colors='Color')
```

假設愛麗絲是不在數據集中的新患者。 如果我告訴你愛麗絲的血紅蛋白水平和血糖水平,你可以預測她是否有 CKD 嘛? 確實看起來可以! 你可以在這里看到非常清晰的規律:右下角的點代表沒有 CKD 的人,其余的傾向于有 CKD 的人。 對于人來說,規律是顯而易見的。 但是,我們如何為計算機編程來自動檢測這種規律?
### 最近鄰分類器
我們可能尋找很多種模式,還有很多分類算法。但是我會告訴你一個算法,它擁有令人驚訝的效果。它被稱為最近鄰分類。這是它的思路。如果我們有愛麗絲的血紅蛋白和血糖數值,我們可以把她放在這個散點圖的某個地方;血紅蛋白是她的`x`坐標,血糖是她的`y`坐標。現在,為了預測她是否有 CKD,我們在散點圖中找到最近的點,檢查它是藍色還是金色;我們預測愛麗絲應該接受與該患者相同的診斷。
換句話說,為了將 Alice 劃分為 CKD 與否,我們在訓練集中找到與 Alice “最近”的患者,然后將該患者的診斷用作對 Alice 的預測。直覺上,如果散點圖中的兩個點彼此靠近,那么相應的測量結果非常相似,所以我們可能會預計,他們(更可能)得到相同的診斷。我們不知道 Alice 的診斷,但是我們知道訓練集中所有病人的診斷,所以我們在訓練集中找到與 Alice 最相似的病人,并利用病人的診斷來預測 Alice 的診斷。
在下圖中,紅點代表愛麗絲。它與距離它最近的點由一條黑線相連,即訓練集中最近鄰。該圖由一個名為`show_closest`的函數繪制。它需要一個數組,代表 Alice 點的`x和`y`坐標。改變它們來查看最近的點如何改變!特別注意最近的點是藍色,以及金色的時候。
```py
# In this example, Alice's Hemoglobin attribute is 0 and her Glucose is 1.5.
alice = make_array(0, 1.5)
show_closest(alice)
```

因此,我們的最近鄰分類器是這樣工作的:
+ 找到訓練集中離新點最近的點。
+ 如果最近的點是“CKD”點,則將新點劃分為“CKD”。如果最近的點是“非 CKD”點,則將新點劃分為“非 CKD”。
散點圖表明這個最近鄰分類器應該相當準確。右下角的點傾向于接受“非 CKD”的診斷,因為他們的最近鄰是一個金點。其余的點傾向于接受“CKD”診斷,因為他們的最近鄰是藍點。所以這個例子中,最近鄰策略似乎很好地捕捉了我們的直覺。
## 決策邊界
有時一種分類器可視化的實用方法是,繪制出分類器預測“CKD”的幾種屬性,以及預測“非 CKD”的幾種。我們最終得到兩者之間的邊界,邊界一側的點將被劃分為“CKD”,而另一側的點將劃分為“非 CKD”。這個邊界稱為決策邊界。每個不同的分類器將有不同的決策邊界;決策邊界只是一種方法,用于可視化分類器實用什么標準來對點分類。
例如,假設愛麗絲的點坐標是`(0, 1.5)`。注意最近鄰是藍色的。現在嘗試減少點的高度(`y`坐標)。你會看到,在`y = 0.95`左右,最近鄰從藍色變為金色。
```py
alice = make_array(0, 0.97)
show_closest(alice)
```

這里有數百個未分類的新點,都是紅色的。

每個紅點在訓練集中都有一個最近鄰(與之前的藍點和金點相同)。對于一些紅點,你可以很容易地判斷最近鄰是藍色還是金色。對于其他點來說,通過眼睛來做出決定更為棘手。那些是靠近決策邊界的點。
但是計算機可以很容易地確定每個點的最近鄰。那么讓我們將我們的最近鄰分類器應用于每個紅點:
對于每個紅點,它必須找到訓練集中最近的點;它必須將紅點的顏色改變為最近鄰的顏色。
結果圖顯示哪些點將劃分為“CKD”(全部為藍色),或者“非 CKD”(全部為金色)。

決策邊界是分類器從將紅點轉換為藍色變成金色的地方。
## KNN
然而,兩個類別的分類并不總是那么清晰。例如,假設我們不用血紅蛋白水平而是看白細胞計數。看看會發生什么:
```py
ckd.scatter('White Blood Cell Count', 'Glucose', colors='Color')
```

如你所見,非 CKD 個體都聚集在左下角。大多數 CKD 患者在該簇的上方或右側,但不是全部。上圖左下角有一些 CKD 患者(分散在金簇中的少數藍點表示)。這意味著你不能從這兩個檢測結果確定,某些人是否擁有 CKD。
如果提供愛麗絲的血糖水平和白細胞計數,我們可以預測她是否患有慢性腎病嘛?是的,我們可以做一個預測,但是我們不應該期望它是 100% 準確的。直覺上,似乎存在預測的自然策略:繪制 Alice 在散點圖中的位置;如果她在左下角,則預測她沒有 CKD,否則預測她有 CKD。
這并不完美 - 我們的預測有時是錯誤的。 (請花點時間思考一下,會把哪些患者弄錯?)上面的散點圖表明,CKD 患者的葡萄糖和白細胞水平有時與沒有 CKD 的患者相同,因此任何分類器都是不可避免地會對他們做出錯誤的預測。
我們可以在計算機上自動化嗎?那么,最近鄰分類器也是一個合理的選擇。花點時間思考一下:它的預測與上述直覺策略的預測相比如何?他們什么時候會不同?
它的預測與我們的直覺策略非常相似,但偶爾會做出不同的預測。特別是,如果愛麗絲的血液檢測結果恰好把她放在左下角的一個藍點附近,那么這個直觀的策略就可能預測“非 CKD”,而最近鄰的分類器會預測“CKD”。
最近鄰分類器有一個簡單的推廣,修正了這個異常。它被稱為 K 最近鄰分類器。為了預測愛麗絲的診斷,我們不僅僅查看靠近她的一個鄰居,而是查看靠近她的三個點,并用這三個點中的每一個點的診斷來預測艾麗絲的診斷。特別是,我們將使用這 3 個診斷中的大部分值作為我們對 Alice 診斷的預測。當然,數字 3 沒有什么特別之處:我們可以使用 4 或 5 或更多。 (選擇一個奇數通常是很方便的,所以我們不需要處理相等)。一般來說,我們選擇一個數字`k`,而我們對 Alice 的預測診斷是基于訓練集中最接近愛麗絲的`k`個點。直觀來說,這些是血液測試結果與愛麗絲最相似的`k`個患者,因此使用他們的診斷來預測愛麗絲的診斷似乎是合理的。
## 訓練和測試
我們最近的鄰居分類器有多好?要回答這個問題,我們需要知道我們的分類有多正確。如果患者患有慢性腎臟疾病,那么我們的分類器有多可能將其選出來呢?
如果病人在我們的訓練集中,我們可以立即找到。我們已經知道病人位于什么類別,所以我們可以比較我們的預測和病人的真實類別。
但是分類器的重點在于對未在訓練集中的新患者進行預測。我們不知道這些病人位于什么類別,但我們可以根據分類器做出預測。如何知道預測是否正確?
一種方法是等待患者之后的醫學檢查,然后檢查我們的預測是否與檢查結果一致。用這種方法,當我們可以說我們的預測有多準確的時候,它就不再能用于幫助病人了。
相反,我們將在一些真實類別已知的病人上嘗試我們的分類器。然后,我們將計算分類器正確的時間比例。這個比例將作為我們分類器準確預測的所有新患者的比例的估計值。這就是所謂的測試。
## 過于樂觀的“測試”
訓練集提供了一組非常吸引人的患者,我們在它們上測試我們的分類器,因為我們可以知道訓練集中每個患者的分類。
但是,我們要小心,如果我們走這條道路,前面就會有隱患。一個例子會告訴我們為什么。
假設我們使用 1 鄰近分類器,根據血糖和白細胞計數來預測患者是否患有慢性腎病。
```py
ckd.scatter('White Blood Cell Count', 'Glucose', colors='Color')
```

之前,我們說我們預計得到一些分類錯誤,因為在左下方有一些藍色和金色的點。
但是訓練集中的點,也就是已經在散點圖上的點呢?我們會把它們誤分類嗎?
答案是否。請記住,1 最近鄰分類尋找訓練集中離被分類點最近的點。那么,如果被分類的點已經在訓練集中,那么它在訓練集中的最近鄰就是它自己!因此它將被劃分為自己的顏色,這將是正確的,因為訓練集中的每個點都已經被正確著色。
換句話說,如果我們使用我們的訓練集來“測試”我們的 1 鄰近分類器,分類器將以 100% 的幾率內通過測試。
任務完成。多好的分類器!
不,不是。正如我們前面提到的,左下角的一個新點很容易被誤分類。 “100% 準確”是一個很好的夢想,而它持續。
這個例子的教訓是不要使用訓練集來測試基于它的分類器。
### 生成測試集
在前面的章節中,我們看到可以使用隨機抽樣來估計符合一定標準的總體中的個體比例。不幸的是,我們剛剛看到訓練集不像所有患者總體中的隨機樣本,在一個重要的方面:我們的分類器正確猜測訓練集中的個體,比例高于總體中的個體。
當我們計算數值參數的置信區間時,我們希望從一個總體中得到許多新的隨機樣本,但是我們只能訪問一個樣本。我們通過從我們的樣本中自舉重采樣來解決這個問題。
我們將使用一個類似的想法來測試我們的分類器。我們將從原始訓練集中創建兩個樣本,將其中一個樣本作為我們的訓練集,另一個用于測試。
所以我們將有三組個體:
+ 訓練集,我們可以對它進行任何大量的探索來建立我們的分類器
+ 一個單獨的測試集,在它上面測試我們的分類器,看看分類的正確比例是多少
+ 個體的底層總體,我們不了解它;我們的希望是我們的分類器對于這些個體也會成功,就像我們的測試集一樣。
如何生成訓練和測試集?你猜對了 - 我們會隨機選擇。
`ckd`有 158 個個體。讓我們將它們隨機的一半用于訓練,另一半用于測試。為此,我們將打亂所有行,把前 79 個作為訓練集,其余的 79 個用于測試。
```py
shuffled_ckd = ckd.sample(with_replacement=False)
training = shuffled_ckd.take(np.arange(79))
testing = shuffled_ckd.take(np.arange(79, 158))
```
現在讓我們基于訓練樣本中的點構造我們的分類器:
```py
training.scatter('White Blood Cell Count', 'Glucose', colors='Color')
plt.xlim(-2, 6)
plt.ylim(-2, 6);
```

我們得到以下分類區域和決策邊界:

把測試數據放在這個圖上,你可以立刻看到分類器對于幾乎所有的點都正確,但也有一些錯誤。 例如,測試集的一些藍點落在分類器的金色區域。

盡管存在一些錯誤,但分類器看起來在測試集上表現得相當好。 假設原始樣本是從底層總體中隨機抽取的,我們希望分類器在整個總體上具有相似的準確性,因為測試集是從原始樣本中隨機選取的。
## 表的行
現在我們對最近鄰分類有一個定性的了解,是時候實現我們的分類器了。
在本章之前,我們主要處理表格的單列。 但現在我們必須看看一個個體是否“接近”另一個個體。 個體數據包含在表格的行中。
那么讓我們首先仔細看一下行。
這里是原始表格`ckd`,包含慢性腎病患者資料。
```py
ckd = Table.read_table('ckd.csv').relabeled('Blood Glucose Random', 'Glucose')
```
對應第一個患者的數據在表中第 0 行,與 Python 的索引系統一致。 `Table`的`row`方法將行索引作為其參數來訪問行。
```py
ckd.row(0)
Row(Age=48, Blood Pressure=70, Specific Gravity=1.0049999999999999, Albumin=4, Sugar=0, Red Blood Cells='normal', Pus Cell='abnormal', Pus Cell clumps='present', Bacteria='notpresent', Glucose=117, Blood Urea=56, Serum Creatinine=3.7999999999999998, Sodium=111, Potassium=2.5, Hemoglobin=11.199999999999999, Packed Cell Volume=32, White Blood Cell Count=6700, Red Blood Cell Count=3.8999999999999999, Hypertension='yes', Diabetes Mellitus='no', Coronary Artery Disease='no', Appetite='poor', Pedal Edema='yes', Anemia='yes', Class=1)
```
行擁有自己的數據類型:它們是行對象。 注意屏幕不僅顯示行中的值,還顯示相應列的標簽。
行通常不是數組,因為它們的元素可以是不同的類型。 例如,上面那行的一些元素是字符串(如`'abnormal'`),有些是數字。 所以行不能被轉換成數組。
但是,行與數組有一些特征。 你可以使用`item`來訪問行中的特定元素。 例如,要訪問患者 0 的白蛋白水平,我們可以查看上面那行的打印輸出中的標簽,發現它是第 3 項:
```py
ckd.row(0).item(3)
4
```
### 將行轉換為數組(可能的時候)
元素都是數字(或都是字符串)的行可以轉換為數組。 將行轉換為數組可以讓我們訪問算術運算和其他漂亮的 NumPy 函數,所以它通常很有用。
回想一下,在上一節中,我們試圖根據血紅蛋白和血糖兩個屬性將患者劃分為“CKD”或“非 CKD”,這兩個屬性都是以標準單位測量的。
```py
ckd = Table().with_columns(
'Hemoglobin', standard_units(ckd.column('Hemoglobin')),
'Glucose', standard_units(ckd.column('Glucose')),
'Class', ckd.column('Class')
)
color_table = Table().with_columns(
'Class', make_array(1, 0),
'Color', make_array('darkblue', 'gold')
)
ckd = ckd.join('Class', color_table)
ckd
```
| Class | Hemoglobin | Glucose | Color |
| --- | --- | --- | --- |
| 0 | 0.456884 | 0.133751 | gold |
| 0 | 1.153 | -0.947597 | gold |
| 0 | 0.770138 | -0.762223 | gold |
| 0 | 0.596108 | -0.190654 | gold |
| 0 | -0.239236 | -0.49961 | gold |
| 0 | -0.0304002 | -0.159758 | gold |
| 0 | 0.282854 | -0.00527964 | gold |
| 0 | 0.108824 | -0.623193 | gold |
| 0 | 0.0740178 | -0.515058 | gold |
| 0 | 0.83975 | -0.422371 | gold |
(省略了 148 行)
下面是兩個屬性的散點圖,以及新患者 Alice 對應的紅點。 她的血紅蛋白值是 0(即平均值)和血糖為 1.1(即比平均值高 1.1 個 SD)。
```py
alice = make_array(0, 1.1)
ckd.scatter('Hemoglobin', 'Glucose', colors='Color')
plots.scatter(alice.item(0), alice.item(1), color='red', s=30);
```

為了找到 Alice 點和其他點之間的距離,我們只需要屬性的值:
```py
ckd_attributes = ckd.select('Hemoglobin', 'Glucose')
ckd_attributes
```
| Hemoglobin | Glucose |
| --- | --- |
| 0.456884 | 0.133751 |
| 1.153 | -0.947597 |
| 0.770138 | -0.762223 |
| 0.596108 | -0.190654 |
| -0.239236 | -0.49961 |
| -0.0304002 | -0.159758 |
| 0.282854 | -0.00527964 |
| 0.108824 | -0.623193 |
| 0.0740178 | -0.515058 |
| 0.83975 | -0.422371 |
(省略了 148 行)
每行由我們的訓練樣本中的一個點的坐標組成。 由于行現在只包含數值,因此可以將它們轉換為數組。 為此,我們使用函數`np.array`,將任何類型的有序對象(如行)轉換為數組。 (我們的老朋友`make_array`用于創建數組,而不是用于將其他類型的序列轉換為數組。)
```py
ckd_attributes.row(3)
Row(Hemoglobin=0.59610766482326683, Glucose=-0.19065363034327712)
np.array(ckd_attributes.row(3))
array([ 0.59610766, -0.19065363])
```
這非常方便,因為我們現在可以在每行的數據上使用數組操作了。
### 只有兩個屬性時點的距離
我們需要做的主要計算是,找出 Alice 的點與其他點之間的距離。 為此,我們需要的第一件事就是計算任意一對點之間的距離。
我們如何實現呢? 在二維空間中,這非常簡單。 如果我們在坐標`(x0, y0)`處有一個點,而在`(x1, y1)`處有另一個點,則它們之間的距離是:
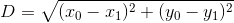
(這是從哪里來的?它來自勾股定理:我們有一個直角三角形,邊長為`x0 - x1`和`y0 - y1`,我們想要求出斜邊的長度。)
在下一節中,我們將看到,當存在兩個以上的屬性時,這個公式有個直接的擴展。 現在,讓我們使用公式和數組操作來求出 Alice 和第 3 行病人的距離。
```py
patient3 = np.array(ckd_attributes.row(3))
alice, patient3
(array([ 0. , 1.1]), array([ 0.59610766, -0.19065363]))
distance = np.sqrt(np.sum((alice - patient3)**2))
distance
1.4216649188818471
```
我們需要 Alice 和一堆點之間的距離,所以讓我們寫一個稱為距離的函數來計算任意一對點之間的距離。 該函數將接受兩個數組,每個數組包含一個點的`(x, y)`坐標。 (記住,那些實際上是患者的血紅蛋白和血糖水平。)
```py
def distance(point1, point2):
"""Returns the Euclidean distance between point1 and point2.
Each argument is an array containing the coordinates of a point."""
return np.sqrt(np.sum((point1 - point2)**2))
distance(alice, patient3)
1.4216649188818471
```
我們已經開始建立我們的分類器:距離函數是第一個積木。 現在讓我們來研究下一個片段。
### 在整個行上使用`apply`
回想一下,如果要將函數應用于表的列的每個元素,一種方法是調用`table_name.apply(function_name, column_label)`。 當我們在列的每個元素上調用該函數時,它求值為由函數返回值組成的數組。所以數組的每個條目都基于表的相應行。
如果使用`apply`而不指定列標簽,則整行將傳遞給該函數。 讓我們在一個非常小的表格上,看看它的工作原理,表格包含訓練樣本中前五個患者的信息。
```py
t = ckd_attributes.take(np.arange(5))
t
```
| Hemoglobin | Glucose |
| --- | --- |
| 0.456884 | 0.133751 |
| 1.153 | -0.947597 |
| 0.770138 | -0.762223 |
| 0.596108 | -0.190654 |
| -0.239236 | -0.49961 |
舉個例子,假設對于每個病人,我們都想知道他們最不尋常的屬性是多么的不尋常。 具體而言,如果患者的血紅蛋白水平遠高于其血糖水平,我們想知道它離平均值有多遠。 如果她的血糖水平遠遠高于她的血紅蛋白水平,那么我們想知道它離平均值有多遠。
這與獲取兩個量的絕對值的最大值是一樣的。 為了為特定的行執行此操作,我們可以將行轉換為數組并使用數組操作。
```py
def max_abs(row):
return np.max(np.abs(np.array(row)))
max_abs(t.row(4))
0.49961028259186968
```
現在我們可以將`max_abs`應用于`t`表的每一行:
```py
t.apply(max_abs)
array([ 0.4568837 , 1.15300352, 0.77013762, 0.59610766, 0.49961028])
```
這種使用`apply`的方式幫助我們創建分類器的下一個積木。
### Alice 的 K 最近鄰
如果我們想使用 K 最近鄰分類器來劃分 Alice,我們必須確定她的 K 個最近鄰。 這個過程中的步驟是什么? 假設`k = 5`。 然后這些步驟是:
+ 步驟 1:的是 Alice 與訓練樣本中每個點之間的距離。
+ 步驟 2:按照距離的升序對數據表進行排序。
+ 步驟 3:取得有序表的前 5 行。
步驟 2 和步驟 3 似乎很簡單,只要我們有了距離。 那么我們來關注步驟 1。
這是愛麗絲:
```py
alice
array([ 0. , 1.1])
```
我們需要一個函數,它可以求出 Alice 和另一個點之間的距離,它的坐標包含在一行中。 `distance`函數返回任意兩點之間的距離,他們的坐標位于數組中。 我們可以使用它來定義`distance_from_alice`,它將一行作為參數,并返回該行與 Alice 之間的距離。
```py
def distance_from_alice(row):
"""Returns distance between Alice and a row of the attributes table"""
return distance(alice, np.array(row))
distance_from_alice(ckd_attributes.row(3))
1.4216649188818471
```
現在我們可以調用`apply`,將`distance_from_alice`函數應用于`ckd_attributes`的每一行,第一步完成了。
```py
distances = ckd_attributes.apply(distance_from_alice)
ckd_with_distances = ckd.with_column('Distance from Alice', distances)
ckd_with_distances
```
| Class | Hemoglobin | Glucose | Color | Distance from Alice |
| --- | --- | --- | --- | --- |
| 0 | 0.456884 | 0.133751 | gold | 1.06882 |
| 0 | 1.153 | -0.947597 | gold | 2.34991 |
| 0 | 0.770138 | -0.762223 | gold | 2.01519 |
| 0 | 0.596108 | -0.190654 | gold | 1.42166 |
| 0 | -0.239236 | -0.49961 | gold | 1.6174 |
| 0 | -0.0304002 | -0.159758 | gold | 1.26012 |
| 0 | 0.282854 | -0.00527964 | gold | 1.1409 |
| 0 | 0.108824 | -0.623193 | gold | 1.72663 |
| 0 | 0.0740178 | -0.515058 | gold | 1.61675 |
| 0 | 0.83975 | -0.422371 | gold | 1.73862 |
(省略了 148 行)
對于步驟 2,讓我們以距離的升序對表排序:
```py
sorted_by_distance = ckd_with_distances.sort('Distance from Alice')
sorted_by_distance
```
| Class | Hemoglobin | Glucose | Color | Distance from Alice |
| --- | --- | --- | --- | --- |
| 1 | 0.83975 | 1.2151 | darkblue | 0.847601 |
| 1 | -0.970162 | 1.27689 | darkblue | 0.986156 |
| 0 | -0.0304002 | 0.0874074 | gold | 1.01305 |
| 0 | 0.14363 | 0.0874074 | gold | 1.02273 |
| 1 | -0.413266 | 2.04928 | darkblue | 1.03534 |
| 0 | 0.387272 | 0.118303 | gold | 1.05532 |
| 0 | 0.456884 | 0.133751 | gold | 1.06882 |
| 0 | 0.178436 | 0.0410639 | gold | 1.07386 |
| 0 | 0.00440582 | 0.025616 | gold | 1.07439 |
| 0 | -0.169624 | 0.025616 | gold | 1.08769 |
(省略了 148 行)
步驟 3:前五行對應 Alice 的五個最近鄰;你可以將五替換為任意正整數。
```py
alice_5_nearest_neighbors = sorted_by_distance.take(np.arange(5))
alice_5_nearest_neighbors
```
| Class | Hemoglobin | Glucose | Color | Distance from Alice |
| --- | --- | --- | --- | --- |
| 1 | 0.83975 | 1.2151 | darkblue | 0.847601 |
| 1 | -0.970162 | 1.27689 | darkblue | 0.986156 |
| 0 | -0.0304002 | 0.0874074 | gold | 1.01305 |
| 0 | 0.14363 | 0.0874074 | gold | 1.02273 |
| 1 | -0.413266 | 2.04928 | darkblue | 1.03534 |
愛麗絲五個最近鄰中有三個是藍點,兩個是金點。 所以 5 鄰近的分類器會把愛麗絲劃分為藍色:它可能預測愛麗絲有慢性腎病。
下面的圖片放大了愛麗絲和她五個最近鄰。 這兩個金點就在紅點正下方的圓圈內。 分類器說,愛麗絲更像她身邊的三個藍點。

我們正在實現我們的 K 最近鄰分類器。 在接下來的兩節中,我們將把它放在一起并評估其準確性。
## 實現分類器
現在我們準備基于多個屬性實現 K 最近鄰分類器。 到目前為止,我們只使用了兩個屬性,以便可視化。 但通常預測將基于許多屬性。 這里是一個例子,顯示了多個屬性可能比兩個更好。
### 鈔票檢測
這次我們來看看,預測鈔票(例如 20 美元鈔票)是偽造還是合法的。 研究人員根據許多單個鈔票的照片,為我們匯集了一套數據集:一些是假冒的,一些是合法的。 他們從每張圖片中計算出一些數字,使用這門課中我們無需擔心的技術。 所以,對于每一張鈔票,我們知道了一些數字,它們從鈔票的照片以及它的類別(是否是偽造的)中計算。 讓我們把它加載到一個表中,并看一下。
```py
banknotes = Table.read_table('banknote.csv')
banknotes
```
| WaveletVar | WaveletSkew | WaveletCurt | Entropy | Class |
| --- | --- | --- | --- | --- |
| 3.6216 | 8.6661 | -2.8073 | -0.44699 | 0 |
| 4.5459 | 8.1674 | -2.4586 | -1.4621 | 0 |
| 3.866 | -2.6383 | 1.9242 | 0.10645 | 0 |
| 3.4566 | 9.5228 | -4.0112 | -3.5944 | 0 |
| 0.32924 | -4.4552 | 4.5718 | -0.9888 | 0 |
| 4.3684 | 9.6718 | -3.9606 | -3.1625 | 0 |
| 3.5912 | 3.0129 | 0.72888 | 0.56421 | 0 |
| 2.0922 | -6.81 | 8.4636 | -0.60216 | 0 |
| 3.2032 | 5.7588 | -0.75345 | -0.61251 | 0 |
| 1.5356 | 9.1772 | -2.2718 | -0.73535 | 0 |
(省略了 1362 行)
讓我們看看,前兩個數值是否告訴了我們,任何鈔票是否偽造的事情。這里是散點圖:
```py
color_table = Table().with_columns(
'Class', make_array(1, 0),
'Color', make_array('darkblue', 'gold')
)
banknotes = banknotes.join('Class', color_table)
banknotes.scatter('WaveletVar', 'WaveletCurt', colors='Color')
```

非常有趣! 這兩個測量值看起來對于預測鈔票是否偽造有幫助。 然而,在這個例子中,你現在可以看到藍色的簇和金色的簇之間有一些重疊。 這表示基于這兩個數字,很難判斷鈔票是否合法。 不過,你可以使用 K 最近鄰分類器來預測鈔票的合法性。
花點時間想一想:假設我們使用`k = 11`(是假如)。 圖中的哪些部分會得到正確的結果,哪些部分會產生錯誤? 決定邊界是什么樣子?
數據中顯示的規律可能非常亂。 例如,如果使用與圖像不同的一對測量值,我們可以得到以下結果:
```py
banknotes.scatter('WaveletSkew', 'Entropy', colors='Color')
```

似乎存在規律,但它是非常復雜。 盡管如此, K 最近鄰分類器仍然可以使用,并將有效地“發現”規律。 這說明了機器學習有多強大:它可以有效地利用規律,我們不曾預料到它,或者我們打算將其編入計算機。
### 多個屬性
到目前為止,我一直假設我們有兩個屬性,可以用來幫助我們做出預測。如果我們有兩個以上呢?例如,如果我們有 3 個屬性呢?
這里有一個很酷的部分:你也可以對這個案例使用同樣的想法。你需要做的所有事情,就是繪制一個三維散點圖,而不是二維的。你仍然可以使用 K 最近鄰分類器,但現在計算 3 維而不是 2 維距離,它還是有用。可以,很酷!
事實上,2 或 3 沒有什么特別之處。如果你有 4 個屬性,你可以使用 4 維的 K 最近鄰分類器。 5 個屬性?在五維空間里工作。沒有必要在這里停下來!這一切都適用于任意多的屬性。你只需在非常高維的空間中工作。它變得有點奇怪 - 不可能可視化,但沒關系。計算機算法推廣得很好:你需要的所有事情,就是計算距離的能力,這并不難。真是亦可賽艇!
```py
ax = plt.figure(figsize=(8,8)).add_subplot(111, projection='3d')
ax.scatter(banknotes.column('WaveletSkew'),
banknotes.column('WaveletVar'),
banknotes.column('WaveletCurt'),
c=banknotes.column('Color'));
```

真棒!只用 2 個屬性,兩個簇之間有一些重疊(這意味著對于重疊中的一些點,分類器必然犯一些錯誤)。但是當我們使用這三個屬性時,兩個簇幾乎沒有重疊。換句話說,使用這 3 個屬性的分類器比僅使用 2 個屬性的分類器更精確。
這是分類中的普遍現象。每個屬性都可能會給你提供新的信息,所以更多的屬性有時可以幫助你建立一個更好的分類器。當然開銷是,現在我們必須收集更多的信息來衡量每個屬性的值,但是如果這個開銷顯著提高了我們的分類器的精度,那么它可能非常值得。
綜上所述:你現在知道如何使用 K 最近鄰分類,預測是與否的問題的答案,基于一些屬性值,假設你有一個帶有樣本的訓練集,其中正確的預測已知。總的路線圖是這樣的:
找出一些屬性,你認為可能幫助你預測問題的答案。
收集一組訓練樣本,其中你知道屬性值以及正確預測。
為了預測未來,測量屬性的值,然后使用 K 最近鄰分類來預測問題的答案。
### 多維距離
我們知道如何在二維空間中計算距離。 如果我們在坐標`(x0, y0)`處有一個點,而在`(x1, y1)`處有另一個點,則它們之間的距離是:
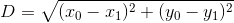
在三維空間中,點是`(x0, y0, z0)`和`(x1, y1, z1)`,它們之間的距離公式為:
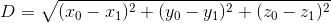
在 N 維空間中,東西有點難以可視化,但我想你可以看到公式是如何推廣的:我們總結每個獨立坐標差的平方,然后取平方根。
在最后一節中,我們定義了函數`distance`返回兩點之間距離。 我們在二維中使用它,但好消息是函數并不關心有多少維! 它只是將兩個坐標數組相減(無論數組有多長),求差值的平方并加起來,然后取平方根。 我們不必更改代碼就可以在多個維度上工作。
```py
def distance(point1, point2):
"""Returns the distance between point1 and point2
where each argument is an array
consisting of the coordinates of the point"""
return np.sqrt(np.sum((point1 - point2)**2))
```
我們在這個新的數據集上使用它。 `wine`表含有 178 種不同的意大利葡萄酒的化學成分。 這些類別是葡萄品種,稱為品種。 有三個類別,但我們只看看是否可以把第一類和其他兩個類別分開。
```py
wine = Table.read_table('wine.csv')
# For converting Class to binary
def is_one(x):
if x == 1:
return 1
else:
return 0
wine = wine.with_column('Class', wine.apply(is_one, 0))
wine
```
| Class | Alcohol | Malic Acid | Ash | Alcalinity of Ash | Magnesium | Total Phenols | Flavanoids | Nonflavanoid phenols | Proanthocyanins | Color Intensity | Hue | OD280/OD315 of diulted wines | Proline |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 1 | 14.23 | 1.71 | 2.43 | 15.6 | 127 | 2.8 | 3.06 | 0.28 | 2.29 | 5.64 | 1.04 | 3.92 | 1065 |
| 1 | 13.2 | 1.78 | 2.14 | 11.2 | 100 | 2.65 | 2.76 | 0.26 | 1.28 | 4.38 | 1.05 | 3.4 | 1050 |
| 1 | 13.16 | 2.36 | 2.67 | 18.6 | 101 | 2.8 | 3.24 | 0.3 | 2.81 | 5.68 | 1.03 | 3.17 | 1185 |
| 1 | 14.37 | 1.95 | 2.5 | 16.8 | 113 | 3.85 | 3.49 | 0.24 | 2.18 | 7.8 | 0.86 | 3.45 | 1480 |
| 1 | 13.24 | 2.59 | 2.87 | 21 | 118 | 2.8 | 2.69 | 0.39 | 1.82 | 4.32 | 1.04 | 2.93 | 735 |
| 1 | 14.2 | 1.76 | 2.45 | 15.2 | 112 | 3.27 | 3.39 | 0.34 | 1.97 | 6.75 | 1.05 | 2.85 | 1450 |
| 1 | 14.39 | 1.87 | 2.45 | 14.6 | 96 | 2.5 | 2.52 | 0.3 | 1.98 | 5.25 | 1.02 | 3.58 | 1290 |
| 1 | 14.06 | 2.15 | 2.61 | 17.6 | 121 | 2.6 | 2.51 | 0.31 | 1.25 | 5.05 | 1.06 | 3.58 | 1295 |
| 1 | 14.83 | 1.64 | 2.17 | 14 | 97 | 2.8 | 2.98 | 0.29 | 1.98 | 5.2 | 1.08 | 2.85 | 1045 |
| 1 | 13.86 | 1.35 | 2.27 | 16 | 98 | 2.98 | 3.15 | 0.22 | 1.85 | 7.22 | 1.01 | 3.55 | 1045 |
前兩種葡萄酒都屬于第一類。為了找到它們之間的距離,我們首先需要一個只有屬性的表格:
```py
wine_attributes = wine.drop('Class')
distance(np.array(wine_attributes.row(0)), np.array(wine_attributes.row(1)))
31.265012394048398
```
中的最后一個葡萄酒是第零類。它與第一個葡萄酒的距離是:
```py
distance(np.array(wine_attributes.row(0)), np.array(wine_attributes.row(177)))
506.05936766351834
```
這也太大了! 讓我們做一些可視化,看看第一類是否真的看起來不同于第零類。
```py
wine_with_colors = wine.join('Class', color_table)
wine_with_colors.scatter('Flavanoids', 'Alcohol', colors='Color')
```

藍點(第一類)幾乎完全與金點分離。 這表明了,為什么兩種第一類葡萄酒之間的距離小于兩個不同類別葡萄酒之間的距離。 我們使用不同的一對屬性,也可以看到類似的現象:
```py
wine_with_colors.scatter('Alcalinity of Ash', 'Ash', colors='Color')
```

但是對于不同的偶對,圖像更加模糊。
```py
wine_with_colors.scatter('Magnesium', 'Total Phenols', colors='Color')
```

讓我們來看看,是否可以基于所有的屬性來實現一個分類器。 之后,我們會看到它有多準確。
### 實現計劃
現在是時候編寫一些代碼來實現分類器了。 輸入是我們要分類的一個點。 分類器的原理是,找到訓練集中的 K 個最近鄰點。 所以,我們的方法將會是這樣:
找出最接近的 K 個點,即訓練集中與點最相似的 K 個葡萄酒。
看看這些 K 個鄰居的類別,并取大多數,找到最普遍的葡萄酒類別。 用它作為我們對點的預測。
所以這將指導我們的 Python 代碼的結構。
```py
def closest(training, p, k):
...
def majority(topkclasses):
...
def classify(training, p, k):
kclosest = closest(training, p, k)
kclosest.classes = kclosest.select('Class')
return majority(kclosest)
```
### 實現步驟 1
為了為腎病數據實現第一步,我們必須計算點到訓練集中每個患者的距離,按照距離排序,并取出訓練集中最接近的 K 個患者。
這就是我們在上一節中使用對應 Alice 的點所做的事情。 我們來概括一下這個代碼。 我們將在這里重新定義`distance`,只是為了方便。
```py
def distance(point1, point2):
"""Returns the distance between point1 and point2
where each argument is an array
consisting of the coordinates of the point"""
return np.sqrt(np.sum((point1 - point2)**2))
def all_distances(training, new_point):
"""Returns an array of distances
between each point in the training set
and the new point (which is a row of attributes)"""
attributes = training.drop('Class')
def distance_from_point(row):
return distance(np.array(new_point), np.array(row))
return attributes.apply(distance_from_point)
def table_with_distances(training, new_point):
"""Augments the training table
with a column of distances from new_point"""
return training.with_column('Distance', all_distances(training, new_point))
def closest(training, new_point, k):
"""Returns a table of the k rows of the augmented table
corresponding to the k smallest distances"""
with_dists = table_with_distances(training, new_point)
sorted_by_distance = with_dists.sort('Distance')
topk = sorted_by_distance.take(np.arange(k))
return topk
```
讓我們看看它如何在我們的葡萄酒數據上工作。 我們只要取第一個葡萄酒,在所有葡萄酒中找到最近的五個鄰居。 請記住,由于這個葡萄酒是數據集的一部分,因此它自己是最近的鄰居。 所以我們應該預計看到,它在列表頂端,后面是其他四個。
首先讓我們來提取它的屬性:
```py
special_wine = wine.drop('Class').row(0)
```
現在讓我們找到它的五個最近鄰:
```py
closest(wine, special_wine, 5)
```
| Class | Alcohol | Malic Acid | Ash | Alcalinity of Ash | Magnesium | Total Phenols | Flavanoids | Nonflavanoid phenols | Proanthocyanins | Color Intensity | Hue | OD280/OD315 of diulted wines | Proline | Distance |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 1 | 14.23 | 1.71 | 2.43 | 15.6 | 127 | 2.8 | 3.06 | 0.28 | 2.29 | 5.64 | 1.04 | 3.92 | 1065 | 0 |
| 1 | 13.74 | 1.67 | 2.25 | 16.4 | 118 | 2.6 | 2.9 | 0.21 | 1.62 | 5.85 | 0.92 | 3.2 | 1060 | 10.3928 |
| 1 | 14.21 | 4.04 | 2.44 | 18.9 | 111 | 2.85 | 2.65 | 0.3 | 1.25 | 5.24 | 0.87 | 3.33 | 1080 | 22.3407 |
| 1 | 14.1 | 2.02 | 2.4 | 18.8 | 103 | 2.75 | 2.92 | 0.32 | 2.38 | 6.2 | 1.07 | 2.75 | 1060 | 24.7602 |
| 1 | 14.38 | 3.59 | 2.28 | 16 | 102 | 3.25 | 3.17 | 0.27 | 2.19 | 4.9 | 1.04 | 3.44 | 1065 | 25.0947 |
好的! 第一行是最近鄰,這是它自己 - `Distance`中值為零,和預期一樣。 所有五個最近鄰都屬于第一類,這與我們先前的觀察結果一致,即第一類葡萄酒集中在某些維度。
### 實現步驟 2 和 3
接下來,我們需要獲取最近鄰的“最大計數”,并把我們的點分配給大多數的相同類別。
```py
def majority(topkclasses):
ones = topkclasses.where('Class', are.equal_to(1)).num_rows
zeros = topkclasses.where('Class', are.equal_to(0)).num_rows
if ones > zeros:
return 1
else:
return 0
def classify(training, new_point, k):
closestk = closest(training, new_point, k)
topkclasses = closestk.select('Class')
return majority(topkclasses)
classify(wine, special_wine, 5)
1
```
如果將`special_wine`改為數據集中的最后一個,我們的分類器是否能夠判斷它在第零類中嘛?
```py
special_wine = wine.drop('Class').row(177)
classify(wine, special_wine, 5)
0
```
是的! 分類器弄對了。
但是我們還不知道它對于所有其它葡萄酒如何,而且無論如何我們都知道,測試已經屬于訓練集的葡萄酒可能過于樂觀了。 在本章的最后部分,我們將葡萄酒分為訓練集和測試集,然后測量分類器在測試集上的準確性。
## 分類器的準確性
為了看看我們的分類器做得如何,我們可以將 50% 的數據放入訓練集,另外 50% 放入測試集。基本上,我們保留一些數據以便以后使用,所以我們可以用它來測量分類器的準確性。我們始終將這個稱為測試集。有時候,人們會把你留下用于測試的數據叫做保留集,他們會把這個估計準確率的策略稱為保留方法。
請注意,這種方法需要嚴格的紀律。在開始使用機器學習方法之前,你必須先取出一些數據,然后放在一邊用于測試。你必須避免使用測試集來開發你的分類器:你不應該用它來幫助訓練你的分類器或者調整它的設置,或者用頭腦風暴的方式來改進你的分類器。相反,在最后你已經完成分類器之后,當你想要它的準確率的無偏估計時,你應該僅僅使用它使用一次。
### 測量我們的葡萄酒分類器的準確率
好吧,讓我們應用保留方法來評估 K 最近鄰分類器識別葡萄酒的有效性。數據集有 178 個葡萄酒,所以我們將隨機排列數據集,并將其中的 89 個放在訓練集中,其余 89 個放在測試集中。
```py
shuffled_wine = wine.sample(with_replacement=False)
training_set = shuffled_wine.take(np.arange(89))
test_set = shuffled_wine.take(np.arange(89, 178))
```
我們將使用訓練集中的 89 個葡萄酒來訓練分類器,并評估其在測試集上的表現。 為了讓我們更輕松,我們將編寫一個函數,在測試集中每個葡萄酒上評估分類器:
```py
def count_zero(array):
"""Counts the number of 0's in an array"""
return len(array) - np.count_nonzero(array)
def count_equal(array1, array2):
"""Takes two numerical arrays of equal length
and counts the indices where the two are equal"""
return count_zero(array1 - array2)
def evaluate_accuracy(training, test, k):
test_attributes = test.drop('Class')
def classify_testrow(row):
return classify(training, row, k)
c = test_attributes.apply(classify_testrow)
return count_equal(c, test.column('Class')) / test.num_rows
```
現在到了答案揭曉的時候了,我們來看看我們做得如何。 我們將任意使用`k = 5`。
```py
evaluate_accuracy(training_set, test_set, 5)
0.9213483146067416
```
對于一個簡單的分類器來說,這個準確率完全不差。
### 乳腺癌診斷
現在我想展示乳腺癌診斷的例子。我受到布列塔尼·溫格(Brittany Wenger)的啟發,他在 2012 年贏得了谷歌科學競賽,還是一位 17 歲的高中生。這是布列塔尼:
布列塔尼的科學競賽項目是構建一個診斷乳腺癌的分類算法。由于她構建了一個精度接近 99% 的算法,她獲得了大獎。
讓我們看看我們能做得如何,使用我們在這個課程中學到的思路。
所以,讓我告訴你一些數據集的信息。基本上,如果一個女性的乳房存在腫塊,醫生可能想要進行活檢,看看它是否是癌癥。有幾個不同的過程用于實現它。布列塔尼專注于細針抽吸(FNA),因為它比替代方案的侵襲性小。醫生得到一塊樣本,放在顯微鏡下,拍攝一張照片,一個訓練有素的實驗室技術人員分析圖像,來確定是否是癌癥。我們得到一張圖片,像下面這樣:
不幸的是,區分良性和惡性可能是棘手的。因此,研究人員已經研究了機器學習的用法,來幫助完成這項任務。我們的想法是,我們要求實驗室技術人員分析圖像并計算各種屬性:諸如細胞的通常大小,細胞大小之間有多少變化等等。然后,我們將嘗試使用這些信息來預測(分類)樣本是否是惡性的。我們有一套來自女性的過去樣本的訓練集,其中正確的診斷已知,我們希望我們的機器學習算法可以使用它們來學習如何預測未來樣本的診斷。
我們最后得到了以下數據集。對于`Class`列,1 表示惡性(癌癥);0 意味著良性(不是癌癥)。
```py
patients = Table.read_table('breast-cancer.csv').drop('ID')
patients
```
| Clump Thickness | Uniformity of Cell Size | Uniformity of Cell Shape | Marginal Adhesion | Single Epithelial Cell Size | Bare Nuclei | Bland Chromatin | Normal Nucleoli | Mitoses | Class |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 5 | 1 | 1 | 1 | 2 | 1 | 3 | 1 | 1 | 0 |
| 5 | 4 | 4 | 5 | 7 | 10 | 3 | 2 | 1 | 0 |
| 3 | 1 | 1 | 1 | 2 | 2 | 3 | 1 | 1 | 0 |
| 6 | 8 | 8 | 1 | 3 | 4 | 3 | 7 | 1 | 0 |
| 4 | 1 | 1 | 3 | 2 | 1 | 3 | 1 | 1 | 0 |
| 8 | 10 | 10 | 8 | 7 | 10 | 9 | 7 | 1 | 1 |
| 1 | 1 | 1 | 1 | 2 | 10 | 3 | 1 | 1 | 0 |
| 2 | 1 | 2 | 1 | 2 | 1 | 3 | 1 | 1 | 0 |
| 2 | 1 | 1 | 1 | 2 | 1 | 1 | 1 | 5 | 0 |
| 4 | 2 | 1 | 1 | 2 | 1 | 2 | 1 | 1 | 0 |
(省略了 673 行)
所以我們有 9 個不同的屬性。 我不知道如何制作它們全部的 9 維散點圖,所以我要挑選兩個并繪制它們:
```py
color_table = Table().with_columns(
'Class', make_array(1, 0),
'Color', make_array('darkblue', 'gold')
)
patients_with_colors = patients.join('Class', color_table)
patients_with_colors.scatter('Bland Chromatin', 'Single Epithelial Cell Size', colors='Color')
```

這個繪圖完全是誤導性的,因為有一堆點的`x`坐標和`y`坐標都有相同的值。 為了更容易看到所有的數據點,我將為`x`和`y`值添加一點點隨機抖動。 這是看起來的樣子:

例如,你可以看到有大量的染色質為 2 和上皮細胞大小為 2 的樣本;所有都不是癌癥。
請記住,抖動僅用于可視化目的,為了更容易感知數據。 我們現在已經準備好使用這些數據了,我們將使用原始數據(沒有抖動)。
首先,我們將創建一個訓練集和一個測試集。 數據集有 683 名患者,因此我們將隨機排列數據集,并將其中的 342 個放在訓練集中,其余的 341 個放在測試集中。
```py
shuffled_patients = patients.sample(683, with_replacement=False)
training_set = shuffled_patients.take(np.arange(342))
test_set = shuffled_patients.take(np.arange(342, 683))
```
讓我們選取 5 個最近鄰,并觀察我們的分類器如何。
```py
evaluate_accuracy(training_set, test_set, 5)
0.967741935483871
```
準確性超過 96%。不錯!這樣一個簡單的技術再一次相當不錯。
作為腳注,你可能已經注意到布列塔尼·溫格做得更好了。 她使用了什么技術? 一個關鍵的創新是,她將置信評分納入了結果:她的算法有一種方法來確定何時無法做出有把握的預測,對于那些患者,甚至不嘗試預測他們的診斷。 她的算法對于做出預測的病人是 99% 準確的,所以這個擴展看起來有點幫助。
## 多元回歸
現在我們已經探索了使用多個屬性來預測類別變量的方法,讓我們返回來預測定量變量。 預測數值量被稱為回歸,多個屬性進行回歸的常用方法稱為多元線性回歸。
### 房價
下面的房價和屬性數據集在愛荷華州埃姆斯市收集了數年。 數據集的描述在線顯示。 我們將僅僅關注列的一個子集。 我們將嘗試從其它列中預測價格列。
```py
all_sales = Table.read_table('house.csv')
sales = all_sales.where('Bldg Type', '1Fam').where('Sale Condition', 'Normal').select(
'SalePrice', '1st Flr SF', '2nd Flr SF',
'Total Bsmt SF', 'Garage Area',
'Wood Deck SF', 'Open Porch SF', 'Lot Area',
'Year Built', 'Yr Sold')
sales.sort('SalePrice')
```
| SalePrice | 1st Flr SF | 2nd Flr SF | Total Bsmt SF | Garage Area | Wood Deck SF | Open Porch SF | Lot Area | Year Built | Yr Sold |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 35000 | 498 | 0 | 498 | 216 | 0 | 0 | 8088 | 1922 | 2006 |
| 39300 | 334 | 0 | 0 | 0 | 0 | 0 | 5000 | 1946 | 2007 |
| 40000 | 649 | 668 | 649 | 250 | 0 | 54 | 8500 | 1920 | 2008 |
| 45000 | 612 | 0 | 0 | 308 | 0 | 0 | 5925 | 1940 | 2009 |
| 52000 | 729 | 0 | 270 | 0 | 0 | 0 | 4130 | 1935 | 2008 |
| 52500 | 693 | 0 | 693 | 0 | 0 | 20 | 4118 | 1941 | 2006 |
| 55000 | 723 | 363 | 723 | 400 | 0 | 24 | 11340 | 1920 | 2008 |
| 55000 | 796 | 0 | 796 | 0 | 0 | 0 | 3636 | 1922 | 2008 |
| 57625 | 810 | 0 | 0 | 280 | 119 | 24 | 21780 | 1910 | 2009 |
| 58500 | 864 | 0 | 864 | 200 | 0 | 0 | 8212 | 1914 | 2010 |
(省略了 1992 行)
銷售價格的直方圖顯示出大量的變化,分布顯然不是正態。 右邊的長尾包含幾個價格非常高的房屋。 左邊的短尾不包含任何售價低于 35,000 美元的房屋。
```py
sales.hist('SalePrice', bins=32, unit='$')
```

### 相關性
沒有單個屬性足以預測銷售價格。 例如,第一層面積(平方英尺)與銷售價格相關,但僅解釋其一些變化。
```py
sales.scatter('1st Flr SF', 'SalePrice')
correlation(sales, 'SalePrice', '1st Flr SF')
0.64246625410302249
```

事實上,沒有任何單個屬性與銷售價格的相關性大于 0.7(銷售價格本身除外)。
```py
for label in sales.labels:
print('Correlation of', label, 'and SalePrice:\t', correlation(sales, label, 'SalePrice'))
Correlation of SalePrice and SalePrice: 1.0
Correlation of 1st Flr SF and SalePrice: 0.642466254103
Correlation of 2nd Flr SF and SalePrice: 0.35752189428
Correlation of Total Bsmt SF and SalePrice: 0.652978626757
Correlation of Garage Area and SalePrice: 0.638594485252
Correlation of Wood Deck SF and SalePrice: 0.352698666195
Correlation of Open Porch SF and SalePrice: 0.336909417026
Correlation of Lot Area and SalePrice: 0.290823455116
Correlation of Year Built and SalePrice: 0.565164753714
Correlation of Yr Sold and SalePrice: 0.0259485790807
```
但是,組合屬性可以提供更高的相關性。 特別是,如果我們總結一樓和二樓的面積,那么結果的相關性就比任何單獨的屬性都要高。
```py
both_floors = sales.column(1) + sales.column(2)
correlation(sales.with_column('Both Floors', both_floors), 'SalePrice', 'Both Floors')
0.7821920556134877
```
這種高度相關性表明,我們應該嘗試使用多個屬性來預測銷售價格。 在具有多個觀測屬性和要預測的單個數值(這里是銷售價格)的數據集中,多重線性回歸可能是有效的技術。
## 多元線性回歸
在多元線性回歸中,通過將每個屬性值乘以不同的斜率,從數值輸入屬性預測數值輸出,然后對結果求和。 在這個例子中,第一層的斜率將代表房屋第一層面積的美元每平方英尺,它應該用于我們的預測。
在開始預測之前,我們將數據隨機分成一個相同大小的訓練和測試集。
```py
train, test = sales.split(1001)
print(train.num_rows, 'training and', test.num_rows, 'test instances.')
1001 training and 1001 test instances.
```
多元回歸中的斜率是一個數組,例子中每個屬性擁有一個斜率值。 預測銷售價格包括,將每個屬性乘以斜率并將結果相加。
```py
def predict(slopes, row):
return sum(slopes * np.array(row))
example_row = test.drop('SalePrice').row(0)
print('Predicting sale price for:', example_row)
example_slopes = np.random.normal(10, 1, len(example_row))
print('Using slopes:', example_slopes)
print('Result:', predict(example_slopes, example_row))
Predicting sale price for: Row(1st Flr SF=1092, 2nd Flr SF=1020, Total Bsmt SF=952.0, Garage Area=576.0, Wood Deck SF=280, Open Porch SF=0, Lot Area=11075, Year Built=1969, Yr Sold=2008)
Using slopes: [ 9.99777721 9.019661 11.13178317 9.40645585 11.07998556
11.03830075 10.26908341 10.42534332 11.00103437]
Result: 195583.275784
```
結果是估計的銷售價格,可以將其與實際銷售價格進行比較,以評估斜率是否提供準確的預測。 由于上面的`example_slopes`是隨機選取的,我們不應該期望它們提供準確的預測。
```py
print('Actual sale price:', test.column('SalePrice').item(0))
print('Predicted sale price using random slopes:', predict(example_slopes, example_row))
Actual sale price: 206900
Predicted sale price using random slopes: 195583.275784
```
### 最小二乘回歸
執行多元回歸的下一步是定義最小二乘目標。 我們對訓練集中的每一行執行預測,然后根據實際價格計算預測的均方根誤差(RMSE)。
```py
train_prices = train.column(0)
train_attributes = train.drop(0)
def rmse(slopes, attributes, prices):
errors = []
for i in np.arange(len(prices)):
predicted = predict(slopes, attributes.row(i))
actual = prices.item(i)
errors.append((predicted - actual) ** 2)
return np.mean(errors) ** 0.5
def rmse_train(slopes):
return rmse(slopes, train_attributes, train_prices)
print('RMSE of all training examples using random slopes:', rmse_train(example_slopes))
RMSE of all training examples using random slopes: 69653.9880638
```
最后,我們使用`minimize `函數來找到使 RMSE 最低的斜率。 由于我們想要最小化的函數`rmse_train`需要一個數組而不是一個數字,所以我們必須向`minimize`函數傳遞`array = True`參數。 當使用這個參數時,`minimize`也需要斜率的初始猜測,以便知道輸入數組的維數。 最后,為了加速優化,我們使用`smooth = True`屬性,指出`rmse_train`是一個平滑函數。 計算最佳斜率可能需要幾分鐘的時間。
```py
best_slopes = minimize(rmse_train, start=example_slopes, smooth=True, array=True)
print('The best slopes for the training set:')
Table(train_attributes.labels).with_row(list(best_slopes)).show()
print('RMSE of all training examples using the best slopes:', rmse_train(best_slopes))
The best slopes for the training set:
```
| 1st Flr SF | 2nd Flr SF | Total Bsmt SF | Garage Area | Wood Deck SF | Open Porch SF | Lot Area | Year Built | Yr Sold |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| 73.7779 | 72.3057 | 51.8885 | 46.5581 | 39.3267 | 11.996 | 0.451265 | 538.243 | -534.634 |
```py
RMSE of all training examples using the best slopes: 31146.4442711
```
### 解釋多元線性回歸
讓我們來解釋這些結果。 最佳斜率為我們提供了一個方法,從其房屋屬性估算價格。 一樓的面積約為 75 美元每平方英尺(第一個斜率),而二樓的面積約為 70 元每平方英尺(第二個斜率)。 最后的負值描述了市場:最近幾年的價格平均較低。
大約 3 萬美元的 RMSE 意味著,我們基于所有屬性的銷售價格的最佳線性預測,在訓練集上平均差了大約 3 萬美元。 當預測測試集的價格時,我們發現了類似的誤差,這表明我們的預測方法可推廣到來自同一總體的其他樣本。
```py
test_prices = test.column(0)
test_attributes = test.drop(0)
def rmse_test(slopes):
return rmse(slopes, test_attributes, test_prices)
rmse_linear = rmse_test(best_slopes)
print('Test set RMSE for multiple linear regression:', rmse_linear)
Test set RMSE for multiple linear regression: 31105.4799398
```
如果預測是完美的,那么預測值和實際值的散點圖將是一條斜率為 1 的直線。我們可以看到大多數點落在該線附近,但預測中存在一些誤差。
```py
def fit(row):
return sum(best_slopes * np.array(row))
test.with_column('Fitted', test.drop(0).apply(fit)).scatter('Fitted', 0)
plots.plot([0, 5e5], [0, 5e5]);
```

多元回歸的殘差圖通常將誤差(殘差)與預測變量的實際值進行比較。 我們在下面的殘差圖中看到,我們系統性低估了昂貴房屋的值,由圖右側的許多正的殘差值所示。
```py
test.with_column('Residual', test_prices-test.drop(0).apply(fit)).scatter(0, 'Residual')
plots.plot([0, 7e5], [0, 0]);
```

就像簡單的線性回歸一樣,解釋預測結果至少和預測一樣重要。 很多解釋多元回歸的課程不包含在這個課本中。 完成這門課之后的下一步自然是深入研究線性建模和回歸。
## 最近鄰回歸
另一種預測房屋銷售價格的方法是使用類似房屋的價格。 這個最近鄰的方法與我們的分類器非常相似。 為了加速計算,我們將只使用與原始分析中銷售價格相關性最高的屬性。
```py
train_nn = train.select(0, 1, 2, 3, 4, 8)
test_nn = test.select(0, 1, 2, 3, 4, 8)
train_nn.show(3)
```
| SalePrice | 1st Flr SF | 2nd Flr SF | Total Bsmt SF | Garage Area | Year Built |
| --- | --- | --- | --- | --- | --- |
| 240000 | 1710 | 0 | 1710 | 550 | 2004 |
| 229000 | 1302 | 735 | 672 | 472 | 1996 |
| 136500 | 864 | 0 | 864 | 336 | 1978 |
(省略了 998 行)
最近鄰的計算與最近鄰分類器相同。 在這種情況下,我們將從距離計算中排除`'SalePrice'`而不是`'Class'`列。 第一個測試行的五個最近鄰如下所示。
```py
def distance(pt1, pt2):
"""The distance between two points, represented as arrays."""
return np.sqrt(sum((pt1 - pt2) ** 2))
def row_distance(row1, row2):
"""The distance between two rows of a table."""
return distance(np.array(row1), np.array(row2))
def distances(training, example, output):
"""Compute the distance from example for each row in training."""
dists = []
attributes = training.drop(output)
for row in attributes.rows:
dists.append(row_distance(row, example))
return training.with_column('Distance', dists)
def closest(training, example, k, output):
"""Return a table of the k closest neighbors to example."""
return distances(training, example, output).sort('Distance').take(np.arange(k))
example_nn_row = test_nn.drop(0).row(0)
closest(train_nn, example_nn_row, 5, 'SalePrice')
```
| SalePrice | 1st Flr SF | 2nd Flr SF | Total Bsmt SF | Garage Area | Year Built | Distance |
| --- | --- | --- | --- | --- | --- |
| 150000 | 1299 | 0 | 967 | 494 | 1954 | 51.9711 |
| 144000 | 1344 | 0 | 1024 | 484 | 1958 | 60.8358 |
| 183500 | 1299 | 0 | 1001 | 486 | 1979 | 68.6003 |
| 140000 | 1283 | 0 | 931 | 506 | 1962 | 76.5049 |
| 173000 | 1287 | 0 | 957 | 541 | 1977 | 77.2464 |
預測價格的一個簡單方法是計算最近鄰的價格均值。
```py
def predict_nn(example):
"""Return the majority class among the k nearest neighbors."""
return np.average(closest(train_nn, example, 5, 'SalePrice').column('SalePrice'))
predict_nn(example_nn_row)
158100.0
```
最后,我們可以使用一個測試樣本,檢查我們的預測是否接近真實銷售價格。 看起來很合理!
```py
print('Actual sale price:', test_nn.column('SalePrice').item(0))
print('Predicted sale price using nearest neighbors:', predict_nn(example_nn_row))
Actual sale price: 146000
Predicted sale price using nearest neighbors: 158100.0
```
### 尾注
為了為整個測試集評估這個方法的性能,我們將`predict_nn`應用于每個測試示例,然后計算預測的均方根誤差。 預測的計算可能需要幾分鐘的時間。
```py
nn_test_predictions = test_nn.drop('SalePrice').apply(predict_nn)
rmse_nn = np.mean((test_prices - nn_test_predictions) ** 2) ** 0.5
print('Test set RMSE for multiple linear regression: ', rmse_linear)
print('Test set RMSE for nearest neighbor regression:', rmse_nn)
Test set RMSE for multiple linear regression: 30232.0744208
Test set RMSE for nearest neighbor regression: 31210.6572877
```
對于這些數據,這兩種技術的誤差非常相似! 對于不同的數據集,一種技術可能會勝過另一種。 通過計算兩種技術在同一數據上的均方根誤差,我們可以公平比較這些方法。值得注意的是:表現的差異可能不完全由于技術;這可能由于隨機變化,由于首先對訓練和測試集進行抽樣。
最后,我們可以為這些預測畫出一個殘差圖。 我們仍然低估了最昂貴房屋的價格,但偏差似乎并不像系統性的。 然而,較低價格的殘差非常接近零,這表明較低價格的預測準確性非常高。
```py
test.with_column('Residual', test_prices-nn_test_predictions).scatter(0, 'Residual')
plots.plot([0, 7e5], [0, 0]);
```

