# 十七、更新預測 > 原文：[Updating Predictions](https://github.com/data-8/textbook/tree/gh-pages/chapters/17) > 譯者：[飛龍](https://github.com/wizardforcel) > 協議：[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 我們知道如何使用訓練數據將一個點劃分為兩類之一。 我們的分類只是對類別的預測，基于最接近我們的新點的，訓練點中最常見的類別。 假設我們最終發現了我們的新點的真實類別。 然后我們會知道我們的分類是否正確。 另外，我們將會有一個新點，可以加入到我們的訓練集中，因為我們知道它的類別。 這就更新了我們的訓練集。 所以，我們自然希望，根據新的訓練集更新我們的分類器。 本章將介紹一些簡單的情況，其中新的數據會使我們更新我們的預測。 雖然本章中的例子在計算方面較簡單，但是更新方法可以推廣到復雜的設定，是機器學習最強大的工具之一。 ## “更可能”的二分類器 讓我們嘗試使用數據，將一個點劃分為兩個類別之一，選擇我們認為更可能的類別。 為此，我們不僅需要數據，而且還要清楚地描述幾率是什么樣。 我們將從一個簡單的人造情況開始，開發主要的技術，然后跳到更有趣的例子。 假設有個大學班級，其組成如下： + 60% 的學生為二年級，其余的 40% 是三年級 + 50% 二年級學生已經聲明了他們的專業 + 80% 三年級學生已經聲明了他們的專業 現在假設我從班上隨機挑選一個學生。 你能否用“更可能”的標準，將學生劃分為二年級或三年級？ 你可以，因為這個學生是隨機挑選的，所以你知道這個學生是二年級的幾率是 60%。 這比三年級的 40% 的可能性更大，所以你會把學生劃分為二年級。 專業的信息是無關緊要的，因為我們已經知道班上二，三年的比例。 我們有了非常簡單的分類器！ 但是現在假設我給了你一些被挑選的學生的更多信息： 這個學生已經聲明了專業。 這個知識會改變你的分類嗎？ ## 基于新信息更新預測 現在我們知道學生已經宣布了專業，重要的是要看看年級和專業聲明的關系。 二年級的學生比三年級多，這仍然正確。 但是，三年級的學生，比二年級的學生，聲明專業的比例更高，這也是事實。 我們的分類器必須考慮到這兩個觀察。 為了使這個可視化，我們將使用`students`表，它包含 100 個學生，每個學生一行，學生的年級和專業比例和數據中相同。 ```py students.show(3) ``` | Year | Major | | --- | --- | | Second | Undeclared | | Second | Undeclared | | Second | Undeclared | （省略了 97 行） 為了檢查比例是否正確，我們使用`pivot`，按照這兩個變量對每個學生進行交叉分類。 ```py students.pivot('Major', 'Year') ``` | Year | Declared | Undeclared | | --- | --- | --- | | Second | 30 | 30 | | Third | 32 | 8 |  總人數為 100 人，其中二年級 60 人，三年級 40 人。 二年級中，每個專業類別有 50%。 三年級的 40 人中，20% 是未聲明的，80% 已聲明。 因此，這 100 人的比例和我們問題中的班級相同，我們可以假定，我們的學生是從 100 名學生中隨機抽取的。 我們必須選擇學生最可能進入的那一行。當我們對這個學生一無所知時，他或她可能在四個單元格中的任何一個，因此更可能在第一行（二年級），因為那里包含更多的學生。 但是現在我們知道這個學生已經聲明了專業，所以可能結果的空間已經減少了：現在學生只能在兩個已聲明的單元格中的一個。 這些單元格共有 62 名學生，其中 32 名是三年級。 這是一半以上，即使不是太多。 所以，考慮到學生專業的新信息，我們必須更新我們的預測，現在將學生劃分為三年級。 我們的分類的正確幾率是多少？ 對于所有聲明了專業的 32 個三年級，我們是正確的，對于那 30 個二年級，我們是錯誤的。 因此，我們的正確幾率大約是 0.516。 換句話說，我們正確幾率是聲明專業的學生中三年級的比例。 ```py 32/(30+32) 0.5161290322580645 ``` ## 樹形圖 我們剛剛計算的比例基于 100 名學生。 但是班級沒有理由沒有 200 名學生，只要單元格中的所有比例都是正確的。 那么我們的計算就變成了`64 /(60 + 64)`，就是 0.516。 所以計算只取決于不同類別的比例，而不是計數。 為了便于比較，比例可以用樹形圖可視化，直接顯示在數據透視表下方。 ```py students.pivot('Major', 'Year') ``` | Year | Declared | Undeclared | | --- | --- | --- | | Second | 30 | 30 | | Third | 32 | 8 | 像數據透視表一樣，該圖將學生分成四個不同的組，稱為“分支”。請注意，“三年級已聲明”分支中的學生比例為`0.4 x 0.8 = 0.32`，對應于數據透視表中“三年級已聲明”單元格中的 32 名學生。 “二年級已聲明”分支中包含學生的`0.6 x 0.5 = 0.3`，對應于數據透視表中“二年級已聲明”單元格中的 30 個。 我們知道，被挑選的學生屬于“已聲明”分支。也就是說，學生在兩個頂層分支之一。這兩個分支現在形成了我們的簡化概率空間，所有幾率的計算必須相對于這個簡化空間的總概率。 所以，考慮到學生已聲明專業，他們是三年級的幾率可以直接從樹中計算出來。答案是相對于兩個“已聲明”分類的總比例，“三年級已聲明”分類的比例。 也就是說，答案是和以前一樣，已聲明的學生中三年級的比例。 ```py (0.4 * 0.8)/(0.6 * 0.5 + 0.4 * 0.8) 0.5161290322580645 ``` ### 貝葉斯法則 我們剛剛使用的方法來源于托馬斯·貝葉斯牧師（1701-1761）。他的方法解決了所謂的“逆向概率”問題：假設有了新的數據，如何更新之前發現的幾率？雖然貝葉斯生活在三個世紀之前，但他的方法現在在機器學習中廣泛使用。 我們將在學生總體的背景下講述這個規則。首先，一些術語： 先驗概率。在我們知道所選學生的專業聲明狀態之前，學生是二年級的幾率是 60%，學生是三年級的幾率是 40%。這是兩個類別的先驗概率。 可能性。這是專業狀態在給出學生類別情況下的幾率；因此可以從樹形圖中讀出。例如，假設學生是二年級，已聲明的可能性是 0.5。 后驗概率。這些是考慮專業聲明狀態的信息后，二年級的概率。我們計算了其中的一個： 假設學生已經聲明，學生是三年級的后驗概率表示為 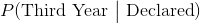，計算如下。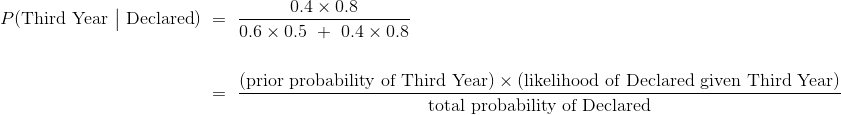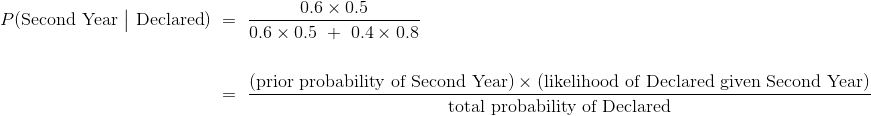  另一個后驗概率是：  ```py (0.6 * 0.5)/(0.6 * 0.5 + 0.4 * 0.8) 0.4838709677419354 ``` 這大概是 0.484，還不到一半，與我們三年的分類一致。 請注意，兩個后驗概率的分母相同：新信息，也就是學生已聲明的幾率。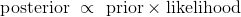 正因為如此，貝葉斯方法有時被歸納為比例陳述：  公式非常便于高效地描述計算。 但是在我們的學生示例這樣的情況中，不用公式來思考更簡單。 我們僅僅使用樹形圖。 ## 做出決策 貝葉斯規則的一個主要用途，是基于不完整的信息做出決策，并在新的信息到來時納入它們。本節指出了在決策時保持你的假設的重要性。 許多疾病的醫學檢測都會返回陽性或陰性結果。陽性結果意味著，根據檢測患者有疾病。陰性結果意味著，檢測的結論是患者沒有這種疾病。 醫學檢測經過精心設計，非常準確。但是很少有檢測是 100% 準確的。幾乎所有檢測都有兩種錯誤： 假陽性是，檢測結果為陽性，但患者沒有該疾病的錯誤。 假陰性是，檢測結果為陰性，但患者確實有這種疾病的錯誤。 這些錯誤可能會影響人們的決策。假陽性可能引起焦慮和不必要的治療（在某些情況下，這是昂貴的或危險的）。如果由于其陰性檢測結果，患者未接受治療，則假陰性可能具有更嚴重的后果。 ### 罕見疾病的檢測 假設總體很大，疾病只占總體的一小部分。 下面的屬性圖總結了這種疾病的信息，以及它的醫學檢測。  總的來說，只有千分之四的總體有這種疾病。 檢測相當準確：假陽性幾率非常小，為 5/1000，但是假陰性更大（盡管還是很小），為 1/100。 個體可能知道也可能不知道他們是否患有這種疾病；通常情況下，人們會進行檢測來確認他們是否擁有。 所以假設隨機從總體中挑選一個人并進行檢測。 如果檢測結果是陽性的，你會如何分類：患病還是沒有患病？ 我們可以通過應用貝葉斯規則，和使用我們的“更可能”的分類器來回答這個問題。 鑒于該人已經檢測出陽性，他或她患病的幾率是相對于`Test Positive`分支中的總比例，頂層分支的比例。 ```py (0.004 * 0.99)/(0.004 * 0.99 + 0.996*0.005 ) 0.44295302013422816 ``` 鑒于這個人已經檢測出陽性，他或她有這種疾病的幾率是大約 44%。 所以我們將它們分類為：沒有疾病。 這是一個奇怪的結論。 我們有一個相當準確的檢測，一個人檢測出陽性，我們的分類是...他們沒有這種疾病？ 這似乎沒有任何意義。 面對一個令人不安的答案，首先要做的是檢查計算。 上面的算法是正確的。 我們來看看是否可以用不同的方式得到相同的答案。 函數`population`群體返回 100,000 名患者的結果表格，它的列展示了實際情況和檢測結果。 檢測與樹中描述的相同。 但是有這種疾病的比例是這個函數的參數。 我們將 0.004 用作參數來調用`population`，然后調用`pivot `，對這十萬人中的每一個人進行交叉分類。 ```py population(0.004).pivot('Test Result', 'True Condition') ``` | True Condition | Negative | Positive | | --- | --- | --- | | Disease | 4 | 396 | | No Disease | 99102 | 498 | 表的單元格計數正確。 例如，根據總體的描述，一千人中有四人患有這種疾病。 表格中有十萬人，所以 400 人應該有這種病。 這就是表格所顯示的：`4 + 396 = 400`。在這 400 認中，99% 獲得了陽性檢測結果：`0.99 x 400 = 396`。 ```py 396/(396 + 498) 0.4429530201342282 ``` 這就是我們通過使用貝葉斯規則得到的答案。`Positives`列中的計數顯示為什么它小于 1/2。 在陽性的人中，更多的人沒有疾病而不是有疾病。 原因是，很大一部分人沒有這種疾病。檢測出假陽性的一小部分人比真陽性要多。 這在樹形圖中更容易可視化：  真陽性的比例是總體一小部分（0.004）的很大一部分（0.99）。 假陽性的比例是總體很大一部分（0.996）的一小部分（0.005）。 這兩個比例是可比的；第二個大一點。 所以，鑒于隨機選擇的人檢測為陽性，我們將他們劃分為，更有可能沒有疾病，是正確的。 ### 主觀先驗 正確并不總令人滿意。將陽性患者劃分為不患有該疾病似乎仍然有些錯誤，對于這樣的精確檢測來說。由于計算是正確的，我們來看看我們的概率計算的基礎：隨機性假設。 我們的假設是，一個隨機選擇的人進行了檢測，并得到了陽性結果。但是這在現實中并沒有發生。因為他們認為他們可能有疾病，或者因為他們的醫生認為他們可能有疾病，人們去接受檢測。被檢測的人不是隨機選擇的總體的成員。 這就是為什么，我們對被檢測者的直覺與我們得到的答案不太相符。我們正在想象一個病人接受檢測的現實情況，因為有一些理由讓他們這樣做，而計算基于隨機選擇的人進行檢測。 所以讓我們在更現實的假設下重做我們的計算，即病人正在接受檢測，因為醫生認為病人有發病的機會。 這里需要注意的是，“醫生認為有機會”是指醫生的意見，而不是總體中的比例。這被稱為主觀概率。在病人是否患有這種疾病的情況下，這也是主觀的先驗概率。 一些研究人員堅持認為，所有的概率必須是相對的頻率，但主觀概率導出都是。候選人贏得下一次選舉的幾率，大地震在下一個十年將會襲擊灣區的幾率，某個國家贏得下一屆足球世界杯的幾率：這些都不是基于相對頻率或長期的頻率。每個都包含主觀因素。涉及它們的所有計算也都有主觀因素。 假設醫生的主觀意見是，患者有 5% 的幾率患病。那么樹形圖中的先驗概率將會改變：  鑒于病人檢測為陽性，他或她有這種疾病的幾率是由貝葉斯規則給出。 ```py (0.05 * 0.99)/(0.05 * 0.99 + 0.95 * 0.005) 0.9124423963133641 ``` 改變先驗的效果是驚人的。 即使病人患病的醫生的先驗概率（5%）很低，一旦患者檢測出陽性，患病的后驗概率高達 91% 以上。 如果患者檢測出陽性，醫生認為患者患病是合理的。 ### 確認結果 雖然醫生的意見是主觀的，但我們可以產生一個人造總體，5% 的人患有這種疾病，并且使用相同的檢測來進行檢測。 然后，我們可以計算不同類別的人數，看看這些計數是否與我們使用貝葉斯規則得到的答案一致。 我們可以使用`population(0.05)`和`pivot`構建相應的總體，并看看四個單元格中的計數。 ```py population(0.05).pivot('Test Result', 'True Condition') ``` | True Condition | Negative | Positive | | --- | --- | --- | | Disease | 50 | 4950 | | No Disease | 94525 | 475 | 在這個人工創建的 10 萬人的總體中，有 5000 人（5%）患有這種疾病，其中 99% 的人檢測為陽性，導致 4950 人為真陽性。 將其與 475 個假陽性相比：在陽性中，擁有疾病的比例與我們通過貝葉斯規則得到的結果相同。 ```py 4950/(4950 + 475) 0.9124423963133641 ``` 因為我們可以一個具有合適比例的總體，我們也可以使用模擬來確認我們的答案是否合理。 `pop_05`表包含 10 萬人的總體，使用醫生的先驗患病概率 5%，以及檢測的錯誤率來生成。 我們從總體中抽取一個規模為 10,000 的簡單隨機樣本，并提取`positive`表，僅包含樣本中陽性檢測結果的個體。 ```py pop_05 = population(0.05) sample = pop_05.sample(10000, with_replacement=False) positive = sample.where('Test Result', are.equal_to('Positive')) ``` 在這些陽性結果中，真實比例是多少？ 那是擁有這種疾病的陽性的比例： ```py positive.where('True Condition', are.equal_to('Disease')).num_rows/positive.num_rows 0.9131205673758865 ``` 運行這兩個單元格幾次，你會發現，陽性中真陽性的比例位于我們通過貝葉斯規則計算的值 0.912 周圍。 你也可以以不同參數調用`population`函數，來改變先驗患病概率，并查看后驗概率如何受到影響。