# 十、假設檢驗
> 原文:[Testing Hypotheses](https://github.com/data-8/textbook/tree/gh-pages/chapters/10)
> 譯者:[飛龍](https://github.com/wizardforcel)
> 協議:[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/)
> 自豪地采用[谷歌翻譯](https://translate.google.cn/)
數據科學家們經常面對世界的是或不是的問題。你在這個課程中看到了一些這樣的問題的例子:
+ 巧克力對你有好處嗎?
+ Broad Street 水泵的水是否會導致霍亂?
+ 加州的人口統計在過去的十年中有所改變嗎?
我們是否回答這些問題取決于我們的數據。加州的人口普查數據可以解決人口統計的問題,而答案幾乎沒有任何不確定性。我們知道 Broad Street 水泵的水源受到霍亂病人的污染,所以我們可以很好地猜測它是否會引起霍亂。
巧克力還是其他任何實驗對你有好處,幾乎肯定要由醫學專家來決定,但是第一步是使用數據科學分析來自研究和隨機實驗的數據。
在本章中,我們將試圖回答這樣的問題,根據樣本和經驗分布的結論。我們將以北加利福尼亞州公民自由聯盟(ACLU)2010 年進行的一項研究為例。
## 陪審團選拔
2010 年,ACLU 在加利福尼亞州阿拉米達縣提交了一份陪審團選擇的報告。報告得出的結論是,在阿拉米達縣的陪審團小組成員中,某些族裔人數不足,并建議對專家組進行一些改革,來合理分配陪審員。在本節中,我們將自己分析數據,并檢查出現的一些問題。
### 陪審團
陪審團是一群被選為準陪審員的人;終審的陪審團是從他們中挑選的。陪審團可以由幾十人或幾千人組成,具體情況取決于審判情況。根據法律,陪審團應該是審判所在社區的代表。加州“民事訴訟法(California's Code of Civil Procedure)”第 197 條規定:“All persons selected for jury service shall be selected at random, from a source or sources inclusive of a representative cross section of the population of the area served by the court.”
最終的陪審團是通過故意納入或排除,從陪審團中挑選出來的。法律允許潛在的陪審員出于醫療原因而被免責;雙方的律師可以從名單上挑選一些潛在的陪審員進行所謂的“先制性反對(peremptory challenges)”。初審法官可以根據陪審團填寫的問卷進行選擇;等等。但最初的陪審團似乎是合格陪審員的總體的隨機樣本。
### 阿拉米達縣的陪審團構成
ACLU 的研究重點是阿拉米達縣陪審團的種族組成。 ACLU 編輯了 2009 年和 2010 年在阿拉米達縣進行的 11 次重罪審判中陪審團的種族組成的數據。在這些陪審團中,報告出庭的陪審員的總人數是 1453 人。ACLU 收集了所有人口的統計數據,并將這些數據與該縣所有合格陪審員的組成進行比較。
數據列在下面的表格中,稱為`jury`。 對于每個種族來說,第一個值就是該種族所有合格的陪審員候選人的比例。 第二個值是出現在出現在陪審團選拔過程的人中,那個種族的人的比例。
```py
jury = Table().with_columns(
'Ethnicity', make_array('Asian', 'Black', 'Latino', 'White', 'Other'),
'Eligible', make_array(0.15, 0.18, 0.12, 0.54, 0.01),
'Panels', make_array(0.26, 0.08, 0.08, 0.54, 0.04)
)
jury
```
| Ethnicity | Eligible | Panels |
| --- | --- | --- |
| Asian | 0.15 | 0.26 |
| Black | 0.18 | 0.08 |
| Latino | 0.12 | 0.08 |
| White | 0.54 | 0.54 |
| Other | 0.01 | 0.04 |
研究中的一些種族代表性過多,一些代表性不足。 條形圖有助于顯示差異。
```py
jury.barh('Ethnicity')
```

### 兩個分布的距離
可視化使我們能夠快速了解,兩個分布之間的相似性和差異。 為了更準確地說出這些差異,我們必須首先量化兩個分布之間的差異。 這將使我們的分析能夠基于更多東西,不僅僅是我們能夠通過眼睛做出的評估。
為了測量兩個分布之間的差異,我們將計算一個數量,稱之為它們之間的總變異距離(total variation distance)。
為了計算總變異距離,我們首先考慮每個類別中兩個比例之間的差異。
```py
# Augment the table with a column of differences between proportions
jury_with_diffs = jury.with_column(
'Difference', jury.column('Panels') - jury.column('Eligible')
)
jury_with_diffs
```
| Ethnicity | Eligible | Panels | Difference |
| --- | --- | --- | --- |
| Asian | 0.15 | 0.26 | 0.11 |
| Black | 0.18 | 0.08 | -0.1 |
| Latino | 0.12 | 0.08 | -0.04 |
| White | 0.54 | 0.54 | 0 |
| Other | 0.01 | 0.04 | 0.03 |
```py
jury_with_diffs.column('Abs. Difference').sum()/2
0.14000000000000001
```
這個數量 0.14 是合格陪審員總體中種族分布與陪審團分布情況之間的總變異距離(TVD)。
只要加上正的差異,我們就可以得到相同的結果。 但是,我們的方法包含所有絕對差異,不需要追蹤哪些差異是正的而哪些不是。
### 計算 TVD 的函數
函數`total_variation_distance`返回兩個數組中的分布的 TVD。
```py
def total_variation_distance(distribution_1, distribution_2):
return np.abs(distribution_1 - distribution_2).sum()/2
```
函數`table_tvd `使用函數`total_variation_distance`來返回表的兩列中的分布的 TVD。
```py
def table_tvd(table, label, other):
return total_variation_distance(table.column(label), table.column(other))
table_tvd(jury, 'Eligible', 'Panels')
0.14000000000000001
```
### 陪審團是否是總體的代表?
現在我們將轉到合格的陪審員和陪審團的 TVD 的值。我們如何解釋 0.14 的距離呢?要回答這個問題,請回想一下,陪審團應該是隨機選擇的。因此,將 0.14 的值與合格的陪審員和隨機選擇的陪審團的 TVD 進行比較,會有幫助。
為了這樣做,我們將在模擬中使用我們的技能。研究共有 1453 名準陪審員。所以讓我們從合格的陪審員的總體中隨機抽取大小為 1453 的樣本。
技術注解。準陪審員的隨機樣本將會不放回地選中。但是,如果樣本的大小相對于總體的大小較小,那么無放回的取樣類似于放回的取樣;總體中的比例在幾次抽取之間變化不大。阿拉米達縣的合格陪審員的總體超過一百萬,與此相比,約 1500 人的樣本量相當小。因此,我們將帶放回地抽樣。
### 從合格的陪審員中隨機抽樣
到目前為止,我們已經使用`np.random.choice`從數組元素中隨機抽樣,并使用`sample `對表的行進行抽樣。 但是現在我們必須從一個分布中抽樣:一組種族以及它們的比例。
為此,我們使用函數`proportions_from_distribution`。 它有三個參數:
+ 表名
+ 包含比例的列的標簽
+ 樣本大小
該函數執行帶放回地隨機抽樣,并返回一個新的表,該表多出了一列`Random Sample`,是隨機樣本中所出現的比例。
所有陪審團的總大小是 1453,所以讓我們把這個數字賦給給一個名成,然后調用:
```py
proportions_from_distribution.
panel_size = 1453
panels_and_sample = proportions_from_distribution(jury, 'Eligible', panel_size)
panels_and_sample
```
| Ethnicity | Eligible | Panels | Random Sample |
| --- | --- | --- | --- |
| Asian | 0.15 | 0.26 | 0.14797 |
| Black | 0.18 | 0.08 | 0.193393 |
| Latino | 0.12 | 0.08 | 0.116311 |
| White | 0.54 | 0.54 | 0.532691 |
| Other | 0.01 | 0.04 | 0.00963524 |
從結果中可以清楚地看出,隨機樣本的分布與合格總體的分布非常接近,與陪審團的分布不同。
和之前一樣,可視化會有幫助。
```py
panels_and_sample.barh('Ethnicity')
```

灰色條形與藍色條形比金色條形更接近。 隨機樣本類似于合格的總體,而不是陪審團。
我們可以通過計算合格總體的分布與隨機樣本之間的 TVD,來量化這一觀察結果。
```py
table_tvd(panels_and_sample, 'Eligible', 'Random Sample')
0.013392980041293877
```
將其與陪審團的距離 0.14 進行比較,可以看到我們在條形圖中看到的數值。 合格總體與陪審團之間的 TVD 為 0.14,但合格總體與隨機樣本之間的 TVD 小得多。
當然,隨機樣本和合格陪審員的分布之間的距離取決于樣本。 再次抽樣可能會給出不同的結果。
### 隨機樣本和總體之間有多少差異?
隨機樣本與合格陪審員的分布之間的 TVD,是我們用來衡量兩個分布之間距離的統計量。 通過重復抽樣過程,我們可以看到不同隨機樣本的統計量是多少。 下面的代碼根據抽樣過程的大量重復,來計算統計量的經驗分布。
```py
# Compute empirical distribution of TVDs
panel_size = 1453
repetitions = 5000
tvds = make_array()
for i in np.arange(repetitions):
new_sample = proportions_from_distribution(jury, 'Eligible', panel_size)
tvds = np.append(tvds, table_tvd(new_sample, 'Eligible', 'Random Sample'))
results = Table().with_column('TVD', tvds)
results
```
| TVD |
| --- |
| 0.0247075 |
| 0.0141569 |
| 0.0138403 |
| 0.0214384 |
| 0.012278 |
| 0.017309 |
| 0.0219752 |
| 0.0192017 |
| 0.02351 |
| 0.00818995 |
(省略了 4990 行)
上面每一行包含大小為 1453 的隨機樣本與合格的陪審員的 TVD。
這一列的直方圖顯示,從合格候選人中隨機抽取 1453 名陪審員的結果是,偏離合格陪審員的種族分布的分布幾乎不超過 0.05。
```py
results.hist(bins=np.arange(0, 0.2, 0.005))
```

### 陪審團和隨機樣本比如何?
然而,研究中的陪審團與合格總體并不十分相似。陪審團和總體之間的 TVD 是 0.14,這距離上面的直方圖的尾部很遠。這看起來不像是隨機樣本和合格總體之間的典型距離。
所以我們的分析支持 ACLU 的計算,即陪審團不是合格陪審員的分布的代表。然而,與大多數這樣的分析一樣,它并沒有說明分布為什么不同,或者差異可能暗示了什么。
ACLU 報告討論了這些差異的幾個可能的原因。例如,一些少數群體在選民登記記錄和機動車輛部門(選擇陪審員的兩個主要來源)的代表性不足。在進行研究時,該縣沒有一個有效的程序,用于跟蹤那些被選中但未出庭的準陪審員。ACLU 列舉了其他幾個原因。不管出于何種原因,似乎很明顯,陪審團的組成與我們對隨機樣本的預期不同,它來自`Eligible`列的分布。
### 數據上的問題
我們已經開發出一種強大的技術,來幫助決定一個分布是否像另一個分布的隨機樣本。但是數據科學不僅僅是技術。特別是數據科學總是需要仔細研究如何收集數據。
合格的陪審員。首先,重要的是要記住,不是每個人都有資格擔任陪審團的職位。阿拉米達縣高級法院在其網站上說:“如果你是18 歲的美國公民,和傳召所在的縣或區的居民,你可能會被要求擔任職位。你必須能夠理解英語,身體上和精神上都有能力擔任,此外,你在過去 12 個月內不得擔任任何類型的陪審員,也沒有被判重罪。
人口普查沒有保存所有這些類別的人口記錄。因此 ACLU 必須以其他方式獲得合格陪審員的人口統計資料。以下是他們對自己所遵循的過程的描述,以及它可能包含的一些缺陷。
“為了確定阿拉米達縣具有陪審團資格的人口的統計數據,我們使用了一個聲明,它為阿拉米達縣人民起訴斯圖亞特·亞歷山大的審判而準備。在聲明中,圣地亞哥州立大學的人口統計學家 Weeks 教授,根據 2000 年的人口普查數據估算了阿拉米達縣的具有陪審團資格的人口,為了得出這個估計值,Weeks 教授考慮到了不符合陪審團擔任條件的人數,因為他們不會說英文,不是公民,因此,他的估計應該是對阿拉米達縣實際具有陪審團資格的人口的準確評估,而不僅僅是審查居住在阿拉米達的所有人口的種族和族裔的人口普查報告。應該指出的是,Weeks 教授所依據的人口普查數據現在已經有十年了,縣的人口統計數據的某些類別,可能已經改變了兩到三個百分點。”
因此,分析中使用的合格陪審員的種族分布本身就是一個估計,可能有點過時。
陪審團。 此外,陪審團并不從整個合格總體中選出。 阿拉米達縣高等法院說:“法院的目標是提供縣人口的準確的橫截面,陪審員的名字是從登記選民和/或車管局發出的駕駛執照中隨機抽取的”。
所有這些都產生了復雜問題,就是如何準確估計阿拉米達縣合格陪審員的種族構成。
目前還不清楚,1453 個陪審團成員如何劃分為不同的種族類別(ACLU 報告稱“律師......合作收集陪審團數據”)。 存在嚴重的社會,文化和政治因素,影響誰被歸類或自我分類到每個種族類別。 我們也不知道陪審團中這些類別的定義,是否與 Weeks 教授所使用的定義相同,Weeks 教授又在它的估算過程中使用了人口普查類別。 因此被比較的兩個分布的對應關系,也存在問題。
### 美國最高法院,1965年:斯溫 VS 阿拉巴馬州
在二十世紀六十年代初期,阿拉巴馬州的塔拉迪加縣,一個名叫羅伯特·斯溫的黑人被指控強奸一名白人婦女,并被判處死刑。
他援引所有陪審團是白人的其他因素,對他的判決提出上訴。當時,只有 21 歲或以上的男子被允許在塔拉迪加縣的陪審團中任職。 在縣里,合格的陪審員中有 26% 是黑人,但在 Swain 的審判中選出的 100 名陪審團中只有 8 名黑人男子。 審判陪審團沒有選定黑人。
1965 年,美國最高法院駁回了斯溫的上訴。 法院在其裁決中寫道:“整體百分比差距很小,沒有反映出包括或排除特定數量的黑人的嘗試”。(... the overall percentage disparity has been small and reflects no studied attempt to include or exclude a specified number of Negroes.)
讓我們用我們開發的方法來檢查,陪審團中的 100 名黑人中的 8 名與合格陪審員的分布之間的差異。
```py
swain_jury = Table().with_columns(
'Ethnicity', make_array('Black', 'Other'),
'Eligible', make_array(0.26, 0.74),
'Panel', make_array(0.08, 0.92)
)
swain_jury
```
| Ethnicity | Eligible | Panel |
| --- | --- | --- |
| Black | 0.26 | 0.08 |
| Other | 0.74 | 0.92 |
```py
table_tvd(swain_jury, 'Eligible', 'Panel')
0.18000000000000002
```
兩個分布之間的 TVD 是 0.18。 這與合格總體的分布和隨機樣本之間的 TVD 比較如何?
為了回答這個問題,我們可以模擬從隨機樣本中計算的 TVD。
```py
# Compute empirical distribution of TVDs
panel_size = 100
repetitions = 5000
tvds = make_array()
for i in np.arange(repetitions):
new_sample = proportions_from_distribution(swain_jury, 'Eligible', panel_size)
tvds = np.append(tvds, table_tvd(new_sample, 'Eligible', 'Random Sample'))
results = Table().with_column('TVD', tvds)
results.hist(bins = np.arange(0, 0.2, 0.01))
```

隨機樣本的 TVD 小于我們所得的值 0.18,它是陪審團和合格陪審員的 TVD。
在這個分析中,數據并沒有像我們以前的分析那樣被問題蓋住 - 涉及的人總數相對較少,而且最高法院案件的統計工作也很仔細。
因此,我們的分析有了明確的結論,那就是陪審團不是總體的代表。 最高法院的判決“整體百分比差距很小”是很難接受的。
## 檢驗的術語
在陪審團選擇的例子的背景下,我們已經形成了一些假設統計檢驗的基本概念。使用統計檢驗作為決策的一種方法是許多領域的標準,并且存在標準的術語。以下是大多數統計檢驗中的步驟順序,以及一些術語和示例。
### 第一步:假設
所有的統計檢驗都試圖在世界的兩種觀點中進行選擇。具體而言,選擇是如何生成數據的兩種觀點之間的選擇。這兩種觀點被稱為假設。
原(零)假設。這就是說,數據在明確指定的假設條件下隨機生成,這些假設使計算幾率成為可能。 “零”一詞強化了這樣一個觀點,即如果數據看起來與零假設的預測不同,那么這種差異只是偶然的。
在阿拉米達縣陪審團選擇的例子中,原假設是從合格的陪審員人群中,隨機抽取這些陪審團。雖然審團的種族組成與合格的陪審員的總體不同,但除了機會變異以外,沒有任何理由存在差異。
備選假設。這就是說,除了幾率以外的某些原因使數據與原假設所預測的數據不同。非正式而言,備選假設認為觀察到的差異是“真實的”。
在我們阿拉米達縣陪審團選擇的例子中,備選假設是,這些小組不是隨機選出來的。除了幾率以外的事情導致了,陪審團的種族組成和合格陪審員總體的種族組成之間存在差異。
### 第二步:檢驗統計量
為了在這兩個假設之間作出決策,我們必須選擇一個統計量作為我們決策的依據。 這被稱為檢驗統計量。
在阿拉米達縣陪審團的例子中,我們使用的檢驗統計量是,陪審團與合格陪審員的總體的種族分布之間的總變異距離。
計算檢驗統計量的觀察值通常是統計檢驗中的第一個計算步驟。 在我們的例子中,陪審團與總體之間的總變異距離的觀察值是 0.14。
### 第三步:檢驗統計量的概率分布,在原假設下
這個步驟把檢驗統計量的觀察值放在一邊,而是把重點放在,如果原假設為真,統計量的值是什么。 在原假設下,由于幾率,樣本可能出現不同的情況。 所以檢驗統計量可能會有所不同。 這個步驟包括在隨機性的原假設下,計算出所有可能的檢驗統計量及其所有概率。
換句話說,在這個步驟中,我們假設原假設為真,并計算檢驗統計量的概率分布。 對于許多檢驗統計量來說,這在數學和計算上都是一項艱巨的任務。 因此,我們通過抽樣過程的大量重復,通過統計量的經驗分布來近似檢驗統計量的概率分布。
在我們的例子中,我們通過直方圖可視化了這個分布。
### 第四步 檢驗的結論
原假設和備選假設之間的選擇,取決于步驟 2 和 3 的結果之間的比較:檢驗統計量的觀察值以及它的分布,就像由原假設預測的那樣。
如果二者一致,則觀察到的檢驗統計量與原假設的預測一致。 換句話說,這個檢驗并不偏向備選假設;數據更加支持原假設。
但如果兩者不一致,就像我們阿拉米達縣陪審團的例子那樣,那么數據就不支持原假設。 這就是為什么我們得出結論,陪審團不是隨機挑選的。 幾率之外的東西影響了他們的構成。
如果數據不支持原假設,我們說檢驗拒絕了原假設。
## 孟德爾的豌豆花
格雷戈·孟德爾(1822-1884)是一位奧地利僧侶,被公認為現代遺傳學領域的奠基人。 孟德爾對植物進行了仔細而大規模的實驗,提出遺傳學的基本規律。
他的許多實驗都在各種豌豆上進行。 他提出了一系列每個品種的假設。 這些被稱為模型。 然后他通過種植植物和收集數據來測試他的模型的有效性。
讓我們分析這樣的實驗的數據,看看孟德爾的模型是否好。
在一個特定的品種中,每個植物具有紫色或白色的花。 每個植物的顏色不受其他植物顏色的影響。 孟德爾推測,植物應隨機具有紫色或白色的花,比例為 3:1。
原假設。 對于每種植物,75% 的幾率是紫色的花,25% 的幾率是白色的花,無論其他植物的顏色如何。
也就是說,原假設是孟德爾的模型是好的。 任何觀察到的模型偏差都是機會變異的結果。
當然,有一個相反的觀點。
備選假設。 孟德爾的模型是無效的。
讓我們看看孟德爾收集的數據更加支持這些假設中的哪一個。
`flowers`表包含了由模型預測的比例,以及孟德爾種植的植物數據。
```py
flowers = Table().with_columns(
'Color', make_array('Purple', 'White'),
'Model Proportion', make_array(0.75, 0.25),
'Plants', make_array(705, 224)
)
flowers
```
| Color | Model Proportion | Plants |
| --- | --- | --- |
| Purple | 0.75 | 705 |
| White | 0.25 | 224 |
共有 929 株植物。 為了觀察顏色的分布是否接近模型預測的結果,我們可以找到觀察到的比例和模型比例之間的總變異距離,就像我們之前那樣。 但是只有兩個類別(紫色和白色),我們有一個更簡單的選擇:我們可以查看紫色的花的比例。 白色的比例沒有新的信息,因為它只是 1 減去紫色的比例。
```py
total_plants = flowers.column('Plants').sum()
total_plants
929
observed_proportion = flowers.column('Plants').item(0)/total_plants
observed_proportion
0.7588805166846071
```
檢驗統計量。 由于該模型預測 75% 的植物花為紫色,相關的統計量是 0.75 與觀察到的花為紫色的植物的比例之間的差異。
```py
observed_statistic = abs(observed_proportion - 0.75)
observed_statistic
0.0088805166846070982
```
這個值與原假設所說的應該的情況相比如何? 為了回答這個問題,我們需要使用模型來模擬植物的新樣本并計算每個樣本的統計量。
我們將首先創建數組`model_colors`,包含顏色,比例由模型給定。 然后我們可以使用`np.random.choice`從這個數組中,帶放回地隨機抽樣 929 次。 根據孟德爾的模型,這就是植物的生成過程。
```py
model_colors = make_array('Purple', 'Purple', 'Purple', 'White')
new_sample = np.random.choice(model_colors, total_plants)
```
> 譯者注:這里可以使用`np.random.choice`的`p`參數來簡化編程。
> ```py
> new_sample = np.random.choice(['Purple', 'White'], total_plants, p=[0.75, 0.25])
> ```
為了與我們觀察到的統計量進行比較,我們需要知道這個新樣本中,花為紫色的植物的比例與 0.75 的差。
```py
proportion_purple = np.count_nonzero(new_sample == 'Purple')/total_plants
abs(proportion_purple - 0.75)
0.016953713670613602
```
檢驗統計量的經驗分布,在原假設為真的情況下。 毫不奇怪,我們得到的值與我們觀察到的統計量之間的差約為 0.00888。 但是如果我們又取了一個樣本,會有多大的不同呢? 你可以通過重新運行上面的兩個單元格來回答這個問題,或者使用`for`循環來模擬統計量。
```py
repetitions = 5000
sampled_stats = make_array()
for i in np.arange(repetitions):
new_sample = np.random.choice(model_colors, total_plants)
proportion_purple = np.count_nonzero(new_sample == 'Purple')/total_plants
sampled_stats = np.append(sampled_stats, abs(proportion_purple - 0.75))
results = Table().with_column('Distance from 0.75', sampled_stats)
results.hist()
```

檢驗的結論。 根據孟德爾的數據,統計量的觀測值是 0.00888,剛好 0.01 以下。 這正好在這個分布的中心。
```py
results.hist()
#Plot the observed statistic as a large red point on the horizontal axis
plots.scatter(observed_statistic, 0, color='red', s=30);
```

基于孟德爾數據的統計量,與我們基于孟德爾模型的模擬的分布是一致的。 因此,與備選假設相比,數據更加支持原假設 - 孟德爾的模型是好的。
## P 值和“一致”的含義
在阿拉米達縣陪審團的例子中,我們觀察到的檢驗統計量顯然與原假設的預測差距很大。在豌豆花的例子中,觀察到的統計量與原假設所預測的分布一致。所以在這兩個例子中,選擇哪個假設是明顯的。
但是有時候這個決策還不是很明顯。觀察到的檢驗統計量是否與原假設預測的分布一致,是一個判斷問題。我們建議你使用檢驗統計量的值以及原假設預測的分布圖,來做出判斷。這將使你的讀者可以自己判斷兩者是否一致。
如果你不想做出自己的判斷,你可以遵循一些慣例。這些慣例基于所謂的觀察到的顯著性水平,或簡稱 P 值。 P 值是一個幾率,使用檢驗統計量的概率分布計算,可以用步驟 3 中的經驗分布來近似。
求出 P 值的實用說明。現在,我們只是給出一個求出該值的機械的方法;意義和解釋放到下一節中。方法:將觀察到的檢驗統計量放在直方圖的橫軸上,求出從以該點起始的尾部比例。這就是 P 值,或者是基于經驗分布的 P 值的相當好的近似值。
```py
empirical_P = np.count_nonzero(sampled_stats >= observed_statistic)/repetitions
empirical_P
0.5508
```
觀察到的統計量 0.00888 非常接近孟德爾模型下所有統計量的中位數。 你可以把它看作是我們之前評論的一個量化,即觀察到的統計量正好在原假設的分布中心。
但是如果離得更遠呢? 例如,如果觀察到的統計量是 0.035 呢? 那么我們會得出什么結論呢?
```py
np.count_nonzero(sampled_stats >= 0.035)/repetitions
0.0122
```
這個比例就很小了。 如果 P 值較小,那就意味著它的尾部很小,所以觀察到的統計量遠離原假設的預測。 這意味著數據支持備選假設而不是支持原假設。
所以如果我們觀察到的統計量是 0.035 而不是 0.00888,我們會選擇備選假設。
那么多小算“小”呢? 這里有個約定。
+ 如果 P 值小于 5%,結果稱為“統計學顯著”。
+ 如果 P 值更小 - 小于 1%,結果被稱為“高度統計學顯著”。
在這兩種情況下,檢驗的結論是數據支持備選假設。
### 約定的歷史注解
上面定義的統計學顯著性的確定,已經在所有應用領域的統計分析中成為標準。當一個約定被如此普遍遵循時,研究它是如何產生的就有趣了。
統計檢驗方法 - 基于隨機樣本數據在假設之間選擇 - 由 Ronald Fisher 爵士在 20 世紀初開發。在 1925 年出版的《寫給研究工作者的統計學方法》(Statistical Methods for Research Workers)一書中的下列陳述中,Ronald 爵士可能在不知情的情況下建立了統計學顯著的約定。對于 5% 的水平,他寫道:“判斷一個偏差是否顯著的時候,將它當做一個極限非常方便。
Ronald 爵士覺得“方便”的東西變成了截斷,獲得了普適常數的地位。無論羅納德爵士如何選出了這個點,這個值是他在眾多值中的個人選擇:在 1926 年的一篇文章中,他寫道:“如果二十分之一看起來還是不夠高,如果我們愿意的話, 我們可以把線畫在百分之二的地方,或者百分之一。個人來說,作者更傾向于把顯著的較低標準設為 5%...”
Fisher 知道“低”是一個判斷問題,沒有獨特的定義。我們建議你遵循他的優秀例子。提供你的數據,作出判斷,并解釋你為什么這樣做。
### GSI 的辯護
假設檢驗是最廣泛使用的統計推斷方法之一。我們已經看到,它的用途十分廣泛,例如審團選擇和豌豆花。在本節的最后一個例子中,我們將在另一個完全不同的語境中對假設進行測試。
伯克利統計班的 350 名學生被分為 12 個討論小組,由研究生導師(GSI)帶領。期中之后后,第三組的學生注意到,他們的成績平均上低于班上的其他人。
在這種情況下,學生們往往會抱怨這一組的 GSI 。他們肯定覺得,GSI 的教學一定是有問題的。否則為什么他們組會比別人做得更差呢?
GSI 通常有更多的統計學經驗,他們的觀點往往是不同的:如果你只是從全班隨機抽取一部分學生,他們的平均分數就可能與學生不滿意的分數相似。
GSI 的立場是一個明確的幾率模型。我們來檢驗一下。
原假設:第三組的平均成績類似于從班上隨機抽取的相同數量的學生的平均成績。
備選假設:不是,太低了。
`scores`包含整個班級的每個學生的小組編號和期中成績。期中成績是 0 到 25 的整數;0 的意思是學生沒來考試。
```py
scores = Table.read_table('scores_by_section.csv')
scores
```
| Section | Midterm |
| --- | --- |
| 1 | 22 |
| 2 | 12 |
| 2 | 23 |
| 2 | 14 |
| 1 | 20 |
| 3 | 25 |
| 4 | 19 |
| 1 | 24 |
| 5 | 8 |
| 6 | 14 |
(省略了 349 行)
這是 12 個小組的平均成績。
```py
scores.group('Section', np.mean).show()
```
| Section | Midterm mean |
| --- | --- |
| 1 | 15.5938 |
| 2 | 15.125 |
| 3 | 13.6667 |
| 4 | 14.7667 |
| 5 | 17.4545 |
| 6 | 15.0312 |
| 7 | 16.625 |
| 8 | 16.3103 |
| 9 | 14.5667 |
| 10 | 15.2353 |
| 11 | 15.8077 |
| 12 | 15.7333 |
第三組平均成績比其他組低一點。 這看起來像機會變異?
我們知道如何找出答案。 我們首先從全班隨機挑選一個“第三組”,看看它的平均得分是多少;然后再做一遍又一遍。
首先,我們需要第三組的學生人數:
```py
scores.group('Section')
```
| Section | count |
| --- | --- |
| 1 | 32 |
| 2 | 32 |
| 3 | 27 |
| 4 | 30 |
| 5 | 33 |
| 6 | 32 |
| 7 | 24 |
| 8 | 29 |
| 9 | 30 |
| 10 | 34 |
(省略了 2 行)
現在我們的計劃是,從班上隨機挑選 27 名學生,并計算他們的平均分數。
所有學生的成績都在一張表上,每個學生一行。 因此,我們將使用`sample`來隨機選擇行,使用`with_replacement = False`選項,以便我們無放回地抽樣。 (稍后我們會看到,結果幾乎與我們通過放回取樣所得到的結果相同)。
```py
scores.sample(27, with_replacement=False).column('Midterm').mean()
13.703703703703704
```
我們已經準備好,模擬隨機的“第三組”的均值的經驗分布。
```py
section_3_mean = 13.6667
repetitions = 10000
means = make_array()
for i in np.arange(repetitions):
new_mean = scores.sample(27, with_replacement=False).column('Midterm').mean()
means = np.append(means, new_mean)
emp_p_value = np.count_nonzero(means <= section_3_mean)/repetitions
print('Empirical P-value:', emp_p_value)
results = Table().with_column('Random Sample Mean', means)
results.hist()
#Plot the observed statistic as a large red point on the horizontal axis
plots.scatter(section_3_mean, 0, color='red', s=30);
Empirical P-value: 0.0581
```

從直方圖來看,第三組的較低均值看起來有些不尋常,但 5% 截斷值的慣例更加偏向 GSI 的假設。 有了這個截斷值,我們說這個結果不是統計學顯著的。
## 錯誤概率
在我們決定我們的數據更加支持哪個假設的過程中,最后一步涉及數據的原假設的一致性判斷。 雖然絕大多數時候這一步都能產生正確的決策,但有時也會讓我們誤入歧途。 原因是機會變異。 例如,即使當原假設為真時,機會變異也可能導致樣本看起來與原假設的預測完全不同。
在本節中,我們將研究假設的統計檢驗如何可能得出這樣的結論,也就是實際上原假設為真時,數據支持備選假設。
由于我們根據 P 值做出決策,現在應該給出一個更正式的定義,而不是“在經驗直方圖的橫坐標上放置觀察到的統計量,并且求出大于它的尾部區域”的機械方法。
### P 值的定義
P 值是在原假設下,檢驗統計量等于在數據中觀察到的值,或甚至在備選假設方向上更進一步的幾率。
讓我們先看看這個定義如何與前一節的計算結果一致。
### 回顧孟德爾的豌豆花
在這個例子中,我們評估孟德爾的豌豆物種的遺傳模型是否良好。 首先回顧一下我們如何建立決策過程,然后在這個背景下考察 P 值的定義。
原假設。 孟德爾的模型是好的:植物的花是紫色或白色,類似于來自總體紫色,紫色,紫色,白色的帶放回隨機樣本。
備選假設。 孟德爾的模型是錯誤的。
檢驗統計量。0.75 與花為紫色的植物的觀察比例的距離:
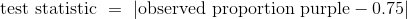
樣本量較大(929),所以如果孟德爾的模型好,那么觀察到的紫色花的比例應該接近 0.75。 如果孟德爾的模型是錯誤的,則觀察到的紫色比例不應該接近0.75,從而使統計值量更大。
因此,在這種情況下,“備選假設的方向”意味著“更大”。
檢驗統計量的觀測值(四舍五入到小數點后五位)是 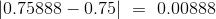。根據定義,P 值是從孟德爾的模型中抽取的樣本,產生 0.00888 或更大的統計量的幾率。
雖然我們還沒有學會如何精確地計算這個幾率,但我們可以通過模擬來逼近它,這就是我們在前一節中所做的。 以下是該部分的所有相關代碼。
```py
# The model and the data
model_colors = make_array('Purple', 'Purple', 'Purple', 'White')
total_plants = 929
observed_statistic = 0.0088805166846070982
# Simulating the test statistic under the null hypothesis
repetitions = 5000
sampled_stats = make_array()
for i in np.arange(repetitions):
new_sample = np.random.choice(model_colors, total_plants)
proportion_purple = np.count_nonzero(new_sample == 'Purple')/total_plants
sampled_stats = np.append(sampled_stats, abs(proportion_purple - 0.75))
# The P-value (an approximation based on the simulation)
empirical_P = np.count_nonzero(sampled_stats >= observed_statistic)/repetitions
# Displaying the results
results = Table().with_column('Distance from 0.75', sampled_stats)
print('Empirical P-value:', empirical_P)
results.hist()
plots.scatter(observed_statistic, 0, color='red', s=30);
Empirical P-value: 0.5436
```

注意 P 值的計算根據孟德爾的模型,基于所有抽取樣本的重復,并且每次都計算檢驗統計量:
```py
empirical_P = np.count_nonzero(sampled_stats >= observed_statistic)/repetitions
empirical_P
0.5436
```
這是統計量大于等于觀測值 0.00888 的樣本比例。
計算結果表明,如果孟德爾的假設是真實的,那么得到一個植物樣本,它的檢驗統計量大于等于孟德爾的觀測值,這個幾率大概是 54%。 這是一個很大的幾率(并且比“較小”的慣例上的 5% 截斷值要大得多)。 因此,孟德爾的數據產生了一個統計量,基于他的模型是不足為奇的,這個數據支持他的模型而不是支持備選假設。
### 回顧 GSI 的辯護
在這個例子中,第三組由一個班級 12 個組中的 27 個學生組成,期中分數均值低于其他組。 我們試圖在以下假設之間作出決策:
原假設:第三組的平均分數類似于從班上隨機挑選的 27 名學生的平均分數。
備選假設:不是,太低了。
檢驗統計量。 抽樣分數的均值。
在這里,備選假設說了,觀察到的平均值太低,并不從隨機抽樣中產生 - 第三組里面有些東西使得平均值較低。
所以在這里,“備選假設的方向”是指“較小”。
檢驗統計量的觀測值是第三組的平均分 13.6667。因此,根據定義,P 值是 27 位隨機選取的學生的平均分 13.6667 或更小的幾率。
這是我們通過近似來模擬的幾率。 這是上一節的代碼。
```py
# The data
scores = Table.read_table('scores_by_section.csv')
sec_3_mean = 13.6667
sec_3_size = 27
# Simulating the test statistic under the null hypothesis
repetitions = 10000
means = make_array()
for i in np.arange(repetitions):
new_mean = scores.sample(sec_3_size, with_replacement=False).column('Midterm').mean()
means = np.append(means, new_mean)
# The P-value (an empirical approximation based on the simulation)
empirical_P = np.count_nonzero(means <= sec_3_mean)/repetitions
# Displaying the results
print('Empirical P-value:', empirical_P)
results = Table().with_column('Random Sample Mean', means)
results.hist()
plots.scatter(sec_3_mean, 0, color='red', s=30);
Empirical P-value: 0.0569
```

經驗 P 值的計算在下面的單元格中。
```py
empirical_P = np.count_nonzero(means <= sec_3_mean)/repetitions
empirical_P
0.0569
```
這是隨機樣本的比例,其中樣本均值小于等于第三組的均值 13.667。
模擬結果顯示,隨機抽樣組的 27 名學生平均分數低于第三組的均值,幾率為大約 6% ??。如果按照傳統的 5% 截斷值作為“較小” P 值的定義,那么 6% 不小了,結果不是統計學顯著的。換句話說,你沒有足夠的證據來拒絕原假設的隨機性。
你可以盡管違背約定,選擇不同的截斷值。如果你這樣做,請記住以下幾點:
+ 始終提供檢驗統計量的觀察值和 P 值,以便讀者可以自行決定 P 值是否小。
+ 只有當傳統的所得結果不符合你的喜好時,才需要違背約定。
+ 即使你的檢驗結論為,第三組平均分數低于隨機抽樣的學生的平均分數,也沒有為什么它較低的信息。
### 做出錯誤決策的概率
這種平均分數的分析產生了一個重要的觀測,關于我們的檢驗做出錯誤結論的概率。
假設你決定使用 5% 的截斷值作為 P 值。 也就是說,如果 P 值低于 5%,那么假設你會選擇備選假設,否則保持原假設。
那么從樣本均值的經驗直方圖可以看出,如果第三組的平均值是 12,那么你會說“太低了”。12 左側的面積不足 5%。
```py
results.hist()
```

13 左邊的面積也不到 5%。 左側面積小于 5% 的所有樣本均值以紅色顯示。

你可以看到,如果第三組的平均值接近 13,并且你使用 5% 的截斷值作為 P 值,那么你應該說小組的均值不像隨機樣本的均值。
你也可以看到,隨機樣本的均值可能在 13 左右(盡管不太可能)。事實上,在我們的模擬中,5000 個隨機樣本中有幾個的均值與 13 相差 0.01 以內。
```py
results.where('Random Sample Mean', are.between(12.99, 13.01)).num_rows
13
```
你看到的是檢驗做出錯誤結論的可能性。
如果你使用了 10% 的截斷值而不是 5%,那么這里的紅色部分意味著,你可能得出結論,它太低了,不能從隨機樣本中產生,即使在你不知情的情況下,它們是來自隨機樣本。

### 做出錯誤決策的幾率
假設你想測試一個硬幣是否均勻。 那么假設是:
原假設:硬幣是均勻的。 也就是說,結果是來自正面和反面的隨機樣本。
備選假設:硬幣不均勻。
假設你的數據基于 400 個硬幣的投擲。 你會預計平等的硬幣能夠在 400 個次投擲中擁有 200 個正面,所以合理的檢驗統計量就是使用 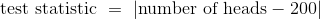。
我們可以在均勻的原假設下模擬統計量。
```py
coin = make_array('Heads', 'Tails')
num_tosses = 400
repetitions = 10000
heads = make_array()
for i in np.arange(repetitions):
tosses = np.random.choice(coin, 400)
heads = np.append(heads, np.count_nonzero(tosses == 'Heads'))
sampled_stats = abs(heads - 200)
results = Table().with_column('|Number of Heads - 200|', sampled_stats)
results.hist(bins = np.arange(0, 45, 5))
```

如果硬幣是不均勻的,那么你預計硬幣的數量就不是 200,或者換句話說,如果硬幣是均勻的,那么你預計,檢驗統計量就會大一些。
因此,正如在孟德爾的豌豆花的例子中,P 值是統計量經驗分布的右側尾部的區域。
假設你決定使用 3.5% 的截斷值作為 P 值。 那么即使硬幣碰巧是均勻的,對于模擬中的 10000 個檢驗統計量的前 3.5%,你也會得出“不均勻”的結論。
換句話說,如果你用3.5% 的 P 值作為臨界值,而硬幣恰好是均勻的,那么大概有 3.5% 的概率你會認為硬幣是不均勻的。
### P 值的截斷值是錯誤概率
上面的例子是一個普遍事實的特例:
如果對 P 值使用`p%`的截斷值,并且原假設恰好是真的,那么大約有`p%`的概率,你的檢驗就會得出結論:備選假設是正確的。
因此,1% 的截斷值比 5% 更保守 - 如果原假設恰好是真的,那么結論為“備選假設”的可能性就會降低。出于這個原因,醫學治療隨機對照試驗通常使用 1% 作為決定以下兩個假設之間的臨界值:
原假設:實驗沒有效果;患者的實驗組和對照組的結果之間的觀察到的差異,是由于隨機性造成的。
備選假設:實驗有效果。
這個想法是,控制結論為實驗有效,而實際上無效的幾率。這減少了給予患者無效治療的風險。
盡管如此,即使你將截斷值設置為 1% 那樣低,并且實驗沒有任何效果,但有大約 1% 的幾率得出結論:實驗是有效的。這由于機會變異。來自隨機樣本的數據很可能最終導致你誤入歧途。
### 數據窺探
上面的討論意味著,如果我們進行 500 個單獨的隨機對照實驗,其中實驗實際上沒有效果,并且每個實驗使用 1% 的截斷值,那么通過機會變異,500 個實驗中的約 5 個將得出結論:實驗確實有效果。
我們可以希望,沒有人會對一無所獲的實驗進行 500 次。但研究人員使用相同的數據測試多個假設并不罕見。例如,在一項關于藥物作用的隨機對照試驗中,研究人員可能會測試該藥物是否對各種不同疾病有影響。
現在假設藥物對任何東西都沒有影響。只是機會變異,一小部分的測試可能會得出結論,它確實有效果。所以,當你閱讀一篇使用假設檢驗的研究,并得出實驗有效的結論時,總是詢問研究人員,在發現所報告的效果之前,究竟檢驗了多少種不同的效果。
如果研究人員在找到給出“高度統計學顯著”的結論之前,進行了多個不同的檢驗,請謹慎使用結果。這項研究可能會受到數據窺探的影響,這實際上意味著將數據捏造成一個假象。
在這種情況下,驗證報告結果的一種方法是,復制實驗并單獨檢驗該特定效果。如果它再次表現為顯著,就驗證了原來的結論。
### 技術注解:其他類型的錯誤
當然,還有另外一種錯誤:認為治療什么也不做,事實上它做了一些事情。近似這個錯誤超出了本節的范圍。要知道,如果你建立你的測試來減少兩個錯誤之一,你幾乎總是增加另一個。
### 技術注解:識別拒絕域
在上面的硬幣投擲的例子中,我們基于 400 次投擲,使用 P 值的 3.5 倍的截斷值來測試硬幣的平等性。檢驗統計量是 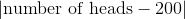。我們在平等的原假設下模擬了這個統計量。
由于所有統計數據的前 3.5%,檢驗的結論是硬幣是不平等的,在下面展示為紅色。

從圖中可以看出,在平等的原假設下,大約前 3.5% 的檢驗統計量的值大于 20。你也可以通過求出這些值的比例來確認:
```py
results.where('|Number of Heads - 200|', are.above_or_equal_to(21)).num_rows/results.num_rows
0.0372
```
也就是說,如果檢驗統計量是 21 或更高,那么以 3.5% 的截斷點,你會得出結論:硬幣是不公平的。
也就是說,如果檢驗統計量是 21 或更高,你將拒絕原假設。因此,“21 以上”的范圍被稱為該檢驗的拒絕域。它對應的正面數量是 221 及以上,或者是 179 及以下。
如果你沒有在直方圖上將其標記為紅色,你將如何找到這些值?百分位數函數在這里派上用場。它需要你嘗試查找的百分比水平以及包含數據的數組。統計量的“前 3.5%”對應于統計量的第 96.5 個百分點:
```py
percentile(96.5, results.column(0))
21.0
```
注意。由于“重復”(即數據中的幾個相同的值)和數據數組的任意長度,百分位數并不總是那么整齊。在本課程的后面,我們將給出一個涵蓋所有情況的百分位數的精確定義。就目前而言,只要認為`percentile `函數返回一個答案,與你直覺上看做百分點的東西相近即可。
## 示例:漏風門
2015 年 1 月 18 日,印第安納波利斯小馬隊(Indianapolis Colts)和新英格蘭愛國者隊(New England Patriots)進行了美式橄欖球大會(AFC)冠軍賽,來確定哪支球隊將晉級超級碗(Super Bowl)。比賽結束后,有人指責愛國者的橄欖球沒有按照規定的要求膨脹,并且更軟。這可能是一個優勢,因為較軟的球可能更容易被捕獲。
幾個星期以來,美國橄欖球界充滿了指責,否認,理論和懷疑:在 20 世紀 70 年代水門事件的政治丑聞之后,新聞界標記了“漏風門”這個話題。國家橄欖球聯盟(NFL)委托了獨立分析小組。在這個例子中,我們將執行我們自己的數據分析。
壓強通常以磅/平方英寸(psi)來衡量。 NFL 規則規定了比賽用球必須充氣為 12.5psi 到 13.5psi 的壓強。每個隊都擁有 12 個球。球隊有責任保持自己的球的壓強,但比賽官方會檢查球。在 AFC 比賽開始之前,所有愛國者的球都在 12.5psi 左右。小馬隊的大部分球在大約 13.0psi。但是,這些賽前數據沒有被記錄下來。
在第二節,小馬隊攔截了一個愛國者的球。在邊線上,他們測量了球的壓強,并確定它低于 12.5psi 的閾值。他們及時通知了官方。
中場休息時,所有的比賽用球都被收集起來檢查。兩名官方人員 Clete Blakeman 和 Dyrol Prioleau 測量了每個球的壓強。這里是數據;壓強的單位是磅/平方英寸。被小馬隊攔截的愛國者的球在這個時候沒有被檢查。大多數小馬隊的球也沒有 - 官方只是耗完了時間,為了下半場的開始,不得不交出了這些球。
```py
football = Table.read_table('football.csv')
football = football.drop('Team')
football.show()
```
| Ball | Blakeman | Prioleau |
| --- | --- | --- |
| Patriots 1 | 11.5 | 11.8 |
| Patriots 2 | 10.85 | 11.2 |
| Patriots 3 | 11.15 | 11.5 |
| Patriots 4 | 10.7 | 11 |
| Patriots 5 | 11.1 | 11.45 |
| Patriots 6 | 11.6 | 11.95 |
| Patriots 7 | 11.85 | 12.3 |
| Patriots 8 | 11.1 | 11.55 |
| Patriots 9 | 10.95 | 11.35 |
| Patriots 10 | 10.5 | 10.9 |
| Patriots 11 | 10.9 | 11.35 |
| Colts 1 | 12.7 | 12.35 |
| Colts 2 | 12.75 | 12.3 |
| Colts 3 | 12.5 | 12.95 |
| Colts 4 | 12.55 | 12.15 |
對于被檢查的 15 個球中的每一個,兩名官員獲得了不同的結果。 在同一物體上重復測量得到不同的結果并不少見,特別是當測量由不同的人進行時。 所以我們將每個球賦為這個球上進行的兩次測量的平均值。
```py
football = football.with_column(
'Combined', (football.column(1)+football.column(2))/2
)
football.show()
```
| Ball | Blakeman | Prioleau | Combined |
| --- | --- | --- | --- |
| Patriots 1 | 11.5 | 11.8 | 11.65 |
| Patriots 2 | 10.85 | 11.2 | 11.025 |
| Patriots 3 | 11.15 | 11.5 | 11.325 |
| Patriots 4 | 10.7 | 11 | 10.85 |
| Patriots 5 | 11.1 | 11.45 | 11.275 |
| Patriots 6 | 11.6 | 11.95 | 11.775 |
| Patriots 7 | 11.85 | 12.3 | 12.075 |
| Patriots 8 | 11.1 | 11.55 | 11.325 |
| Patriots 9 | 10.95 | 11.35 | 11.15 |
| Patriots 10 | 10.5 | 10.9 | 10.7 |
| Patriots 11 | 10.9 | 11.35 | 11.125 |
| Colts 1 | 12.7 | 12.35 | 12.525 |
| Colts 2 | 12.75 | 12.3 | 12.525 |
| Colts 3 | 12.5 | 12.95 | 12.725 |
| Colts 4 | 12.55 | 12.15 | 12.35 |
一眼望去,愛國者隊的壓強顯然低于小馬隊。 由于一些放氣在比賽過程中是正常的,獨立分析師決定計算距離比賽開始的壓強下降值。 回想一下,愛國者的球開始時是大約 12.5psi,小馬隊的球是大約 13.0psi。 因此愛國者球的壓強下降值計算為 12.5 減中場時的壓強,小馬隊的球的壓強下降值為 13.0 減半場的壓強。
我們來構建兩張表,一張是愛國者的數據,一張是小馬的。 每張表的最后一列是距離開始的壓強下降值。
```py
patriots = football.where('Ball', are.containing('Patriots'))
patriots = patriots.with_column('Drop', 12.5-patriots.column('Combined'))
patriots.show()
```
| Ball | Blakeman | Prioleau | Combined | Drop |
| --- | --- | --- | --- | --- |
| Patriots 1 | 11.5 | 11.8 | 11.65 | 0.85 |
| Patriots 2 | 10.85 | 11.2 | 11.025 | 1.475 |
| Patriots 3 | 11.15 | 11.5 | 11.325 | 1.175 |
| Patriots 4 | 10.7 | 11 | 10.85 | 1.65 |
| Patriots 5 | 11.1 | 11.45 | 11.275 | 1.225 |
| Patriots 6 | 11.6 | 11.95 | 11.775 | 0.725 |
| Patriots 7 | 11.85 | 12.3 | 12.075 | 0.425 |
| Patriots 8 | 11.1 | 11.55 | 11.325 | 1.175 |
| Patriots 9 | 10.95 | 11.35 | 11.15 | 1.35 |
| Patriots 10 | 10.5 | 10.9 | 10.7 | 1.8 |
| Patriots 11 | 10.9 | 11.35 | 11.125 | 1.375 |
```py
colts = football.where('Ball', are.containing('Colts'))
colts = colts.with_column('Drop', 13.0-colts.column('Combined'))
colts
```
| Ball | Blakeman | Prioleau | Combined | Drop |
| --- | --- | --- | --- | --- |
| Colts 1 | 12.7 | 12.35 | 12.525 | 0.475 |
| Colts 2 | 12.75 | 12.3 | 12.525 | 0.475 |
| Colts 3 | 12.5 | 12.95 | 12.725 | 0.275 |
| Colts 4 | 12.55 | 12.15 | 12.35 | 0.65 |
看起來好像愛國者的漏氣比小馬隊更大。 自然統計量是兩個平均漏氣之間的差異。 我們將處理它,但你可以自由地用其他自然統計量重復分析,例如整體平均漏氣與愛國者之間的差異。
```py
patriots_mean = patriots.column('Drop').mean()
colts_mean = colts.column('Drop').mean()
observed_statistic = patriots_mean - colts_mean
observed_statistic
0.73352272727272805
```
這種正面的差異反映了這樣的事實,即愛國者的球的平均壓強下降值大于小馬隊。
難道這個差異是偶然的,還是愛國者的下降值太大? 這個問題非常類似于我們之前問過的問題,關于一個大班中的一個小組的成績。就像我們在這個例子中所做的那樣,我們將建立原假設。
原假設:愛國者的下降值就是 15 次下降值中的,大小為 11 的隨機樣本。 由于機會變異,均值比小馬隊高。
備選假設:愛國者的下降值太大,并不僅僅是機會變異的結果。
如果原假設是真的,那么愛國者的下降值就可以對比從 15 次下降值隨機不帶放回抽取的 11 個。 所以讓我們創建一個,含有所有 15 個下降值,并從中隨機抽取。
```py
drops = Table().with_column(
'Drop', np.append(patriots.column('Drop'), colts.column('Drop'))
)
drops.show()
```
| Drop |
| --- |
| 0.85 |
| 1.475 |
| 1.175 |
| 1.65 |
| 1.225 |
| 0.725 |
| 0.425 |
| 1.175 |
| 1.35 |
| 1.8 |
| 1.375 |
| 0.475 |
| 0.475 |
| 0.275 |
| 0.65 |
```py
drops.sample(with_replacement=False).show()
```
| Drop |
| --- |
| 1.225 |
| 1.175 |
| 1.175 |
| 0.475 |
| 1.375 |
| 0.425 |
| 0.85 |
| 0.65 |
| 1.35 |
| 1.65 |
| 0.725 |
| 0.475 |
| 1.475 |
| 1.8 |
| 0.275 |
注意`sample`的使用沒有帶樣本大小。 這是因為`sample`使用的默認樣本大小是表格的行數;如果你不指定樣本大小,則會返回與原始表格大小相同的樣本。 這對于我們的目的非常理想,因為當你不放回抽樣時(通過指定`with_replacement = False`),并且次數與行數相同,最終會對所有行進行隨機洗牌。 運行幾次該單元格來查看輸出如何變化。
我們現在可以使用打亂表的前 11 行作為原假設下的愛國者的下降值的模擬。 剩下的四行形成了對應的小馬隊的下降值的模擬。 我們可以使用這兩個模擬數組來模擬我們在原假設下的檢驗統計量。
```py
shuffled = drops.sample(with_replacement=False)
new_patriots = shuffled.take(np.arange(11))
new_patriots_mean = new_patriots.column(0).mean()
new_colts = shuffled.take(np.arange(11, drops.num_rows))
new_colts_mean = new_colts.column(0).mean()
simulated_stat = new_patriots_mean - new_colts_mean
simulated_stat
-0.70681818181818212
```
運行幾次該單元格來查看檢驗統計量的變化情況。 請記住,模擬是在原假設下,即愛國者的下降值類似于隨機抽樣的 15 個下降值。
現在是我們熟悉的步驟了。 我們將在院假設下重復模擬檢驗統計量。 模擬結束時,數組的`simulated_statistics`將包含所有模擬的檢驗統計量。
```py
simulated_statistics = make_array()
repetitions = 10000
for i in np.arange(repetitions):
shuffled = drops.sample(with_replacement=False)
new_patriots_mean = shuffled.take(np.arange(11)).column(0).mean()
new_colts_mean = shuffled.take(np.arange(11, drops.num_rows)).column(0).mean()
new_statistic = new_patriots_mean - new_colts_mean
simulated_statistics = np.append(simulated_statistics, new_statistic)
```
現在對于經驗 P 值,這是一個幾率(在原假設下計算),所得的檢驗統計量等于觀察到統計量,或者更加偏向備選假設方向。 為了弄清楚如何計算它,重要的是要回憶另一個假設:
備選假設:愛國者的下降值太大,并不僅僅是機會變異的結果。
“備選假設的方向”是愛國者的下降值很大,對應我們的檢驗統計量,“愛國者的均值減去小馬隊的均值”較大。 所以 P 值是幾率(在原假設下計算),所得檢驗統計量大于等于我們 0.73352272727272805。
```py
empirical_P = np.count_nonzero(simulated_statistics >= observed_statistic)/repetitions
empirical_P
0.0027
```
這是一個非常小的 P 值。 為了觀察它,下面是原假設下檢驗統計量的經驗分布,其中觀察到的統計量標在橫軸上。
```py
print('Observed Statistic:', observed_statistic)
print('Empirical P:', empirical_P)
results = Table().with_column('Simulated Statistic', simulated_statistics)
results.hist()
plots.scatter(observed_statistic, 0, color='red', s=30);
Observed Statistic: 0.733522727273
Empirical P: 0.0027
```

請注意,分布大部分集中在 0 左右。在原假設下,愛國者的下降值是所有 15 下降值的隨機樣本,因此小馬對也是如此。 所以這兩組下降值的平均值應該大致相等,因此它們的差值應該在 0 左右。
但是檢驗統計量的觀察值離分布的中心還有很遠的距離。 使用什么是“小”的任何合理的截斷值,經驗 P 值都是小的。 所以我們最終拒絕原假設的隨機性,并得出結論,愛國者的下降值太大,并不單獨反映機會變異。
獨立的調查小組以數種不同的方式分析數據,并考慮到物理定律。最后的報告說:
> “愛國者比賽用球的平均壓降超過了小馬隊的球的平均壓降 0.45psi 至 1.02psi,這取決于所使用的測量儀的各種可能的假設,并假設愛國者的球的初始壓強為 12.5psi,小馬隊的球是 13.0psi。”
> - 2015 年 1 月 18 日,由 NFL 委托對 AFC 冠軍賽的調查報告
我們的分析顯示,平均壓降約為 0.73psi,接近“0.45 至 1.02psi”的中心,因此與官方分析一致。
請記住,我們對假設的檢驗并沒有確定差異不是偶然的原因。 建立因果關系通常比進行假設檢驗更為復雜。
但足球世界里最重要的問題是因果關系:問題是愛國者足球的壓強過大是否是故意的。 如果你對調查人員的答案感到好奇,這里是[完整的報告](https://nfllabor.files.wordpress.com/2015/05/investigative-and-expert-reports-re-footballs-used-during-afc-championsh.pdf)。
