# 十一、估計
> 原文:[Estimation](https://github.com/data-8/textbook/tree/gh-pages/chapters/11)
> 譯者:[飛龍](https://github.com/wizardforcel)
> 協議:[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/)
> 自豪地采用[谷歌翻譯](https://translate.google.cn/)
在前一章中,我們開始開發推斷思維的方法。特別是,我們學會了如何使用數據,在世界的兩個假設之間做決策。但是我們通常只想知道,某件事情有多大。
例如,在前面的章節中,我們調查了敵人可能擁有的戰機數量。在選舉年,我們可能想知道有多少選民贊成特定候選人。為了評估目前的經濟狀況,我們可能會對美國家庭年收入的中位數感興趣。
在本章中,我們將開發一種估計未知參數的方法。請記住,參數是總體相關的數值。
要弄清參數的值,我們需要數據。如果我們有整個人口的相關數據,我們可以簡單地計算參數。
但是,如果人口非常龐大(例如,如果它由美國的所有家庭組成),那么收集整個人口的數據可能過于昂貴和耗時。在這種情況下,數據科學家依賴從人口中隨機抽樣。
這導致了一個推斷問題:如何根據隨機樣本中的數據,對未知參數做出正確的結論?我們將用推斷思維來回答這個問題。
基于隨機樣本的統計量可能是總體中未知參數的合理估計。例如,你可能希望使用家庭樣本的年收入中位數,來估計美國所有家庭的年收入中位數。
但任何統計量的值都取決于樣本,樣本基于隨機抽取。所以每次數據科學家得到了一個基于隨機樣本的估計,他們都面臨一個問題:
“如果樣本是不同的,這個估計有多大的不同呢?”
在本章中,你將學習一種回答這個問題的方法。答案將為你提供工具來估算數值參數,并量化估算中的誤差量。
我們將以百分位數開始。最有名的百分位數是中位數,通常用于收入數據的摘要。在我們即將開發的估計方法中,其他百分位數也是非常重要的。所以我們一開始要仔細定義百分位數。
## 百分位數
數值數據可以按照升序或降序排序。因此,數值數據集的值具有等級順序。百分位數是特定等級的值。
例如,如果你的考試成績在第 95 個百分位,一個常見的解釋是只有 5% 的成績高于你的成績。中位數是第 50 個百分位;通常假定數據集中 50% 的值高于中值。
但是,給予百分位一個精確定義,適用于所有等級和所有列表,需要一些謹慎。為了明白為什么,考慮一個極端的例子,一個班級的所有學生在考試中得分為 75 分。那么 75 是中位數的自然候選,但是 50% 的分數高于 75 并不是真的。另外,75 同樣是第 95 個或第 25 個百分位數,或任何其他百分位數的自然候選。在定義百分位數時,必須將重復 - 也就是相同的數據值 - 考慮在內。
當相關的索引不明確時,你還必須小心列表到底有多長。例如,10 個值的集合的第 87 個百分位數是多少?有序集合的第 8 個值,還是第 9 個,還是其中的某個位置?
### 數值的例子
在給出所有百分位數的一般定義之前,我們將把數值集合的第80個百分點定義為集合中的(一定條件的)最小值,它至少與所有值的 80% 一樣大。
例如,考慮非洲,南極洲,亞洲,北美洲和南美洲五大洲的大小,四舍五入到最接近的百萬平方英里。
```py
sizes = make_array(12, 17, 6, 9, 7)
```
第 80 個百分位數是(一定條件的)最小值,至少和 80% 的值一樣大,也就是五個元素的五分之四。等于 12:
```py
np.sort(sizes)
array([ 6, 7, 9, 12, 17])
```
第 80 個百分位數是列表中的一個值,也就是 12。你可以看到,80% 的值小于等于它,并且它是列表中滿足這個條件的最小值。
與之類似,第 70 個百分位數是該集合中(一定條件的)最小值,至少與 70% 的元素一樣大。 現在 5 個元素中的 70% 是“3.5 個元素”,所以第 70 個百分位數是列表中的第 4 個元素。 它是 12,與這些數據的第 80 百分位數相同。
### `percentile`函數
`percentile`函數接受兩個參數:一個 0 到 100 之間的等級,和一個數組。它返回數組相應的百分位數。
```py
percentile(70, sizes)
12
```
### 一般定義
令`p`為 0 到 100 之間的數字。集合的第`p`個百分位數是集合中的(一定條件)的最小值,它至少與`p%`的所有值一樣大。
通過這個定義,可以計算任何值的集合的任何 0 到 100 之間的百分位數,并且它始終是集合的一個元素。
實際上,假設集合中有`n`個元素。 要找到第`p`個百分位數:
+ 對集合升序排序。
+ 計算`n`的`p%`:`(p/100) * n`。叫做`k`。
+ 如果`k`是一個整數,則取有序集合的第`k`個元素。
+ 如果`k`不是一個整數,則將其四舍五入到下一個整數,并采用有序集合的那個元素。
### 示例
`scores_and_sections`表包含 359 名學生,每個學生一行。 列是學生的討論分組和期中分數。
```py
scores_and_sections = Table.read_table('scores_by_section.csv')
scores_and_sections
```
| Section | Midterm |
| --- | --- |
| 1 | 22 |
| 2 | 12 |
| 2 | 23 |
| 2 | 14 |
| 1 | 20 |
| 3 | 25 |
| 4 | 19 |
| 1 | 24 |
| 5 | 8 |
| 6 | 14 |
(省略了 349 列)
```py
scores_and_sections.select('Midterm').hist(bins=np.arange(-0.5, 25.6, 1))
```

分數的第 85 個百分位數是多少? 為了使用`percentile`函數,創建包含期中分數的數組`scores`,并找到第 85 個百分位數:
```py
scores = scores_and_sections.column(1)
percentile(85, scores)
22
```
根據`percentile`函數,第 85 個百分點數是 22。為了檢查這是否符合我們的新定義,我們直接應用定義。
首先,把分數升序排列:
```py
sorted_scores = np.sort(scores_and_sections.column(1))
```
數組中有 359 個分數。所以下面,計算 359 的 85%,它是 305.15。
```py
0.85 * 359
305.15
```
這不是一個整數。 根據我們的定義,中位數是`sorted_scores`的第 306 個元素,按 Python 的索引約定,它是數組的第 305 項。
```py
# The 306th element of the sorted array
sorted_scores.item(305)
22
```
它和我們通過使用`percentile`得到的答案一樣。以后,我們會僅僅使用`percentile`。
### 四分位數
數值集合的第一個四分位數是第 25 個百分分數。 這個術語(quartile)來自第一個季度(quarter)。 第二個四分位數是中位數,第三個四分位數是第 75 個百分位數。
對于我們的分數數據,這些值是:
```py
percentile(25, scores)
11
percentile(50, scores)
16
percentile(75, scores)
20
```
分數的分布有時歸納為“中等 50%”區間,在第一和第三個四分位數之間。
## 自舉法
一個數據科學家正在使用隨機樣本中的數據來估計未知參數。她使用樣本來計算用作估計值的統計量。
一旦她計算出了統計量的觀察值,她就可以把它作為她的估計值,然后順其自然。 但她是一名數據科學家。 她知道她的隨機樣本只是眾多可能的隨機樣本之一,因此她的估計只是眾多合理估算之一。
這些估計的變化有多大? 為了回答這個問題,似乎她需要從總體中抽取另一個樣本,并根據新樣本計算一個新的估計值。 但是她沒有資源來回到總體中,再抽取一個樣本。
這個數據科學家看起來好像卡住了。
幸運的是,一個叫做自舉法的好主意可以幫助她。 由于從總體中生成新樣本是不可行的,自舉法通過稱為重采樣的方法生成新的隨機樣本:新樣本從原始樣本中隨機抽取。
在本節中,我們將看到自舉法的工作方式和原因。 在本章的其余部分,我們將使用自舉法進行推理。
### 舊金山市的雇員薪資
[SF OpenData](https://data.sfgov.org/) 是一個網站,舊金山市和縣在上面公開提供他們的一些數據。 其中一個數據集包含城市雇員的薪資數據。 其中包括市營醫院的醫療專業人員,警察,消防員,運輸工人,民選官員以及市內所有其他雇員。
2015 日歷年的薪資數據見表`sf2015`。
```py
sf2015 = Table.read_table('san_francisco_2015.csv')
sf2015
```
| Year Type | Year | Organization Group Code | Organization Group | Department Code | Department | Union Code | Union | Job Family Code | Job Family | Job Code | Job | Employee Identifier | Salaries | Overtime | Other Salaries | Total Salary | Retirement | Health/Dental | Other Benefits | Total Benefits | Total Compensation |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| Calendar | 2015 | 2 | Public Works, Transportation & Commerce | WTR | PUC Water Department | 21 | Prof & Tech Engineers - Miscellaneous, Local 21 | 2400 | Lab, Pharmacy & Med Techs | 2481 | Water Qualitytech I/II | 21538 | 82146 | 0 | 0 | 82146 | 16942.2 | 12340.9 | 6337.73 | 35620.8 | 117767 |
| Calendar | 2015 | 2 | Public Works, Transportation & Commerce | DPW | General Services Agency - Public Works | 12 | Carpet, Linoleum and Soft Tile Workers, Local 12 | 7300 | Journeyman Trade | 7393 | Soft Floor Coverer | 5459 | 32165.8 | 973.19 | 848.96 | 33987.9 | 0 | 4587.51 | 2634.42 | 7221.93 | 41209.8 |
| Calendar | 2015 | 4 | Community Health | DPH | Public Health | 790 | SEIU - Miscellaneous, Local 1021 | 1600 | Payroll, Billing & Accounting | 1636 | Health Care Billing Clerk 2 | 41541 | 71311 | 5757.98 | 0 | 77069 | 14697.6 | 12424.5 | 6370.06 | 33492.2 | 110561 |
| Calendar | 2015 | 4 | Community Health | DPH | Public Health | 351 | Municipal Executive Association - Miscellaneous | 0900 | Management | 2620 | Food Service Mgr Administrator | 26718 | 28430.2 | 0 | 763.07 | 29193.3 | 0 | 4223.14 | 5208.51 | 9431.65 | 38625 |
| Calendar | 2015 | 2 | Public Works, Transportation & Commerce | MTA | Municipal Transportation Agency | 790 | SEIU - Miscellaneous, Local 1021 | 8200 | Protection & Apprehension | 8201 | School Crossing Guard | 45810 | 7948.75 | 0 | 0 | 7948.75 | 0 | 2873.17 | 616.24 | 3489.41 | 11438.2 |
| Calendar | 2015 | 1 | Public Protection | POL | Police | 911 | Police Officers' Association | Q000 | Police Services | Q002 | Police Officer | 32906 | 2235 | 0 | 0 | 2235 | 490.36 | 286.72 | 176.57 | 953.65 | 3188.65 |
| Calendar | 2015 | 4 | Community Health | DPH | Public Health | 791 | SEIU - Staff and Per Diem Nurses, Local 1021 | 2300 | Nursing | 2328 | Nurse Practitioner | 7506 | 187247 | 0 | 11704.1 | 198951 | 37683.7 | 12424.5 | 11221.7 | 61329.9 | 260281 |
| Calendar | 2015 | 2 | Public Works, Transportation & Commerce | MTA | Municipal Transportation Agency | 253 | Transport Workers - Transit Operators, Local 250-A | 9100 | Street Transit | 9163 | Transit Operator | 36773 | 66988.5 | 3512.88 | 2770.39 | 73271.8 | 19127.2 | 13203 | 5455.1 | 37785.3 | 111057 |
| Calendar | 2015 | 6 | General Administration & Finance | CAT | City Attorney | 311 | Municipal Attorneys' Association | 8100 | Legal & Court | 8177 | Attorney (Civil/Criminal) | 12963 | 135190 | 0 | 1562.5 | 136752 | 27501.8 | 12424.5 | 10103 | 50029.3 | 186781 |
| Calendar | 2015 | 3 | Human Welfare & Neighborhood Development | DSS | Human Services | 535 | SEIU - Human Services, Local 1021 | 9700 | Community Development | 9703 | Emp & Training Spec 2 | 35179 | 70474.8 | 147.28 | 1647.24 | 72269.3 | 14650.3 | 10696.9 | 5993.11 | 31340.3 | 103610 |
(省略了 42979 行)
共有 42,979 名員工,每個人一行。 有許多列包含市政部門隸屬關系的信息,以及員工薪酬方案不同部分的詳細信息。 這是對應市長 Ed Lee 的一行。
```py
sf2015.where('Job', are.equal_to('Mayor'))
```
| Year Type | Year | Organization Group Code | Organization Group | Department Code | Department | Union Code | Union | Job Family Code | Job Family | Job Code | Job | Employee Identifier | Salaries | Overtime | Other Salaries | Total Salary | Retirement | Health/Dental | Other Benefits | Total Benefits | Total Compensation |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| Calendar | 2015 | 6 | General Administration & Finance | MYR | Mayor | 556 | Elected Officials | 1100 | Administrative & Mgmt (Unrep) | 1190 | Mayor | 22433 | 288964 | 0 | 0 | 288964 | 58117 | 12424.5 | 20293 | 90834.5 | 379798 |
我們要研究最后一欄,總薪酬。 這是員工的工資加上市政府對退休和福利計劃的貢獻。
日歷年的財務方案有時難以理解,因為它們取決于雇用日期,員工是否在城市內部換工作等等。 例如,`Total Compensation`列中的最低值看起來有點奇怪。
```py
sf2015.sort('Total Compensation')
```
| Year Type | Year | Organization Group Code | Organization Group | Department Code | Department | Union Code | Union | Job Family Code | Job Family | Job Code | Job | Employee Identifier | Salaries | Overtime | Other Salaries | Total Salary | Retirement | Health/Dental | Other Benefits | Total Benefits | Total Compensation |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| Calendar | 2015 | 1 | Public Protection | FIR | Fire Department | 798 | Firefighters - Miscellaneous, Local 798 | H000 | Fire Services | H002 | Firefighter | 43833 | 0 | 0 | 0 | 0 | 0 | 0 | -423.76 | -423.76 | -423.76 |
| Calendar | 2015 | 4 | Community Health | DPH | Public Health | 790 | SEIU - Miscellaneous, Local 1021 | 9900 | Public Service Aide | 9924 | PS Aide Health Services | 27871 | -292.4 | 0 | 0 | -292.4 | 0 | -95.58 | -22.63 | -118.21 | -410.61 |
| Calendar | 2015 | 1 | Public Protection | JUV | Juvenile Probation | 790 | SEIU - Miscellaneous, Local 1021 | 8300 | Correction & Detention | 8320 | Counselor, Juvenile Hall | 10517 | 0 | 0 | 0 | 0 | 0 | 0 | -159.12 | -159.12 | -159.12 |
| Calendar | 2015 | 6 | General Administration & Finance | CPC | City Planning | 21 | Prof & Tech Engineers - Miscellaneous, Local 21 | 1000 | Information Systems | 1053 | IS Business Analyst-Senior | 18961 | 0 | 0 | 0 | 0 | 0 | 0 | -26.53 | -26.53 | -26.53 |
| Calendar | 2015 | 6 | General Administration & Finance | CPC | City Planning | 21 | Prof & Tech Engineers - Miscellaneous, Local 21 | 5200 | Professional Engineering | 5277 | Planner 1 | 19387 | 0 | 0 | 0 | 0 | 0 | 0 | -9.51 | -9.51 | -9.51 |
| Calendar | 2015 | 2 | Public Works, Transportation & Commerce | PUC | PUC Public Utilities Commission | 21 | Prof & Tech Engineers - Miscellaneous, Local 21 | 1000 | Information Systems | 1044 | IS Engineer-Principal | 28988 | 0 | 0 | 0 | 0 | 0 | 0 | -3.1 | -3.1 | -3.1 |
| Calendar | 2015 | 1 | Public Protection | JUV | Juvenile Probation | 39 | Stationary Engineers, Local 39 | 7300 | Journeyman Trade | 7335 | Senior Stationary Engineer | 19125 | 0 | 0 | 0 | 0 | 0 | 0 | -0.01 | -0.01 | -0.01 |
| Calendar | 2015 | 1 | Public Protection | ECD | Department of Emergency Management | 351 | Municipal Executive Association - Miscellaneous | 0900 | Management | 0922 | Manager I | 30025 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Calendar | 2015 | 7 | General City Responsibilities | UNA | General Fund Unallocated | 790 | SEIU - Miscellaneous, Local 1021 | 3200 | Recreation | 3280 | Assistant Recreation Director | 49784 | 0 | 0 | 0 | 0 | 0 | 0 | 1.27 | 1.27 | 1.27 |
| Calendar | 2015 | 4 | Community Health | DPH | Public Health | 250 | SEIU - Health Workers, Local 1021 | 2600 | Dietary & Food | 2654 | Cook | 26768 | 0 | 0 | 2.21 | 2.21 | 0 | 0 | 0.17 | 0.17 | 2.38 |
(省略了 42979 行)
為了便于比較,我們將專注于那些工作時間相當于至少半年的人。 最低工資約為每小時 10 美元,52 周每周 20 小時,工資約為 1 萬美元。
```py
sf2015 = sf2015.where('Salaries', are.above(10000))
sf2015.num_rows
36569
```
### 總體和參數
讓這張超過 36500 行的表格成為我們的總體。 這是總薪資的直方圖。
```py
sf_bins = np.arange(0, 700000, 25000)
sf2015.select('Total Compensation').hist(bins=sf_bins)
```

雖然大部分值都低于 300,000 美元,但有一些還是比較高的。 例如,首席投資官的總薪資不多是 65 萬美元。 這就是為什么橫軸延伸到了 700,000 美元。
```py
sf2015.sort('Total Compensation', descending=True).show(2)
```
| Year Type | Year | Organization Group Code | Organization Group | Department Code | Department | Union Code | Union | Job Family Code | Job Family | Job Code | Job | Employee Identifier | Salaries | Overtime | Other Salaries | Total Salary | Retirement | Health/Dental | Other Benefits | Total Benefits | Total Compensation |
| --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- | --- |
| Calendar | 2015 | 6 | General Administration & Finance | RET | Retirement System | 351 | Municipal Executive Association - Miscellaneous | 1100 | Administrative & Mgmt (Unrep) | 1119 | Chief Investment Officer | 46881 | 507832 | 0 | 0 | 507832 | 105053 | 12424.5 | 23566.2 | 141044 | 648875 |
| Calendar | 2015 | 6 | General Administration & Finance | ADM | General Services Agency - City Admin | 164 | Physicians and Dentists - Miscellaneous | 2500 | Med Therapy & Auxiliary | 2598 | Asst Med Examiner | 1016 | 279311 | 3829.36 | 114434 | 397574 | 56211.6 | 12424.5 | 14299.1 | 82935.2 | 480509 |
(省略了 36567 行)
現在讓參數為總薪資的中位數。
既然我們有能力從總體中得到所有數據,我們可以簡單計算參數:
```py
pop_median = percentile(50, sf2015.column('Total Compensation'))
pop_median
110305.78999999999
```
所有員工的薪酬總額的中位數剛剛超過 110,300 美元。
從實際的角度來看,我們沒有理由抽取樣本來估計這個參數,因為我們只是知道它的值。 但在本節中,我們假裝不知道這個值,看看我們如何根據隨機樣本來估計它。
在后面的章節中,我們將回到現實,在參數未知的情況下工作。 就目前而言,我們是無所不知的。
### 隨機樣本和估計
讓我們無放回地隨機抽取 500 名員工的樣本,并將所選員工的總薪酬的中位數作為我們的參數估計量。
```py
our_sample = sf2015.sample(500, with_replacement=False)
our_sample.select('Total Compensation').hist(bins=sf_bins)
```

```py
est_median = percentile(50, our_sample.column('Total Compensation'))
est_median
113598.99000000001
```
樣本量很大。 根據平均定律,樣本的分布與總體的分布相似,因此樣本中位數與總體中位數相差不大(盡管當然并不完全相同)。
所以現在我們有了參數的估計。 但是,如果樣本是不同的,估計的值也會不同。 我們希望能夠量化估計的值在不同樣本間的差異。 這個變化的測量將有助于我們衡量我們可以將參數估計得多么準確。
為了查看樣本有多么不同,我們可以從總體中抽取另一個樣本,但這樣做就作弊了。 我們正試圖模仿現實生活,我們不能掌握所有的人口數據。
用某種方式,我們必須得到另一個隨機樣本,而不從總體中抽樣。
### 自舉法:從樣本中重采樣
我們所做的是,從樣本中隨機抽樣。 我們知道了,大型隨機樣本可能類似于用于抽取的總體。 這一觀察使得數據科學家可以通過自舉來提升自己:抽樣過程可以通過從樣本中抽樣來復制。
以下是自舉法的步驟,用于生成類似總體的另一個隨機樣本:
+ 將原始樣本看做總體。
+ 從樣本中隨機抽取樣本,與原始樣本大小相同。
二次樣本的大小與原始樣本相同很重要。 原因是估計量的變化取決于樣本的大小。 由于我們的原始樣本由 500 名員工組成,我們的樣本中位數基于 500 個值。 為了看看樣本變化多少,我們必須將其與 500 個其他樣本的中位數進行比較。
如果我們從大小為 500 的樣本中,無放回地隨機抽取了 500 次,我們只會得到相同的樣本。 通過帶放回抽取,我們就可以讓新樣本與原始樣本不同,因為有些員工可能會被抽到一次以上,其他人則完全不會。
為什么這是一個好主意? 按照平均定律,原始樣本的分布可能與總體相似,所有“二次樣本”的分布可能與原始樣本相似。 因此,所有二次樣本的分布也可能與總體相似。

### 二次樣本的中位數
回想一下,使用`sample`方法而沒有指定樣本大小時,默認情況下樣本大小等于用于抽取樣本的表的行數。 這是完美的自舉! 這是從原始樣本中抽取的一個新樣本,以及相應的樣本中位數。
```py
resample_1 = our_sample.sample()
resample_1.select('Total Compensation').hist(bins=sf_bins)
```

```py
resampled_median_1 = percentile(50, resample_1.column('Total Compensation'))
resampled_median_1
110001.16
```
通過重采樣,我們有了總體中位數的另一個估計。 通過一次又一次的重采樣,我們得到許多這樣的估計,因此有了估計的經驗分布。
```py
resample_2 = our_sample.sample()
resampled_median_2 = percentile(50, resample_2.column('Total Compensation'))
resampled_median_2
110261.39999999999
```
### 自舉樣本中位數的經驗分布
讓我們定義一個函數`bootstrap_median`,該函數接受我們的原始樣本,包含變量的列的標簽,以及我們想要的自舉樣本的數量,并返回二次樣本的相應中值的數組。
每次我們重采樣并找到中位數,我們重復自舉過程。 所以自舉樣本的數量將被稱為重復數量。
```py
def bootstrap_median(original_sample, label, replications):
"""Returns an array of bootstrapped sample medians:
original_sample: table containing the original sample
label: label of column containing the variable
replications: number of bootstrap samples
"""
just_one_column = original_sample.select(label)
medians = make_array()
for i in np.arange(replications):
bootstrap_sample = just_one_column.sample()
resampled_median = percentile(50, bootstrap_sample.column(0))
medians = np.append(medians, resampled_median)
return medians
```
我們現在將自舉過程重復 5000 次。 數組`bstrap_medians`包含所有 5,000 個自舉樣本的中位數。 注意代碼的運行時間比我們以前的代碼要長。 因為要做很多重采樣!
```py
bstrap_medians = bootstrap_median(our_sample, 'Total Compensation', 5000)
```
這是 5000 個中位數的直方圖。 紅點是總體的參數:它是整個總體的中位數,我們碰巧知道但沒有在自舉過程中使用。
```py
resampled_medians = Table().with_column('Bootstrap Sample Median', bstrap_medians)
#median_bins=np.arange(100000, 130000, 2500)
#resampled_medians.hist(bins = median_bins)
resampled_medians.hist()
plots.scatter(pop_median, 0, color='red', s=30);
```

重要的是要記住,紅點是固定的:110,305.79 美元,總體的中位數。 經驗直方圖是隨機抽取的結果,將相對于紅點隨機定位。
請記住,所有這些計算的重點是估計人口中位數,它是紅點。我們的估計是所有隨機生成的樣本中位數,它們的直方圖你在上面看到了。 我們希望這些估計量包含參數 - 如果沒有,它們就脫線了。
### 估計量是否捕獲了參數
紅點正好落在二次樣本的中位數的經驗直方圖中間,而不是尾部的幾率有多少? 要回答這個問題,我們必須定義“中間”。 讓我們將它看做“紅點落在二次樣本的中位數的中間 95%”。
以下是二次采樣中位數的“中間 95%”的兩端:
```py
left = percentile(2.5, bstrap_medians)
left
107652.71000000001
right = percentile(97.5, bstrap_medians)
right
119256.73
```
總體中位數 110,305 美元在這兩個數中間。下面的直方圖展示了區間和總體中位數。
```py
#median_bins=np.arange(100000, 130000, 2500)
#resampled_medians.hist(bins = median_bins)
resampled_medians.hist()
plots.plot(make_array(left, right), make_array(0, 0), color='yellow', lw=3, zorder=1)
plots.scatter(pop_median, 0, color='red', s=30, zorder=2);
```

我們例子中,估計量的“中間 95%”的區間捕獲了參數。 但是,這是一個偶然嗎?
要查看區間包含參數的頻率,我們必須一遍又一遍地運行整個過程。具體而言,我們將重復以下過程 100 次:
+ 從總體中抽取一個大小為 500 的原始樣本。
+ 執行 5000 次重復的自舉過程,并生成二次樣本的中位數的“中間 95%”的區間。
+ 我們最后得到了 100 個區間,并計算其中有多少個包含總體中位數。
劇透警告:自舉的統計理論表明,這個數字應該在 95 左右。它可能高于或低于 95,但不會離得太遠。
```py
# THE BIG SIMULATION: This one takes several minutes.
# Generate 100 intervals, in the table intervals
left_ends = make_array()
right_ends = make_array()
total_comps = sf2015.select('Total Compensation')
for i in np.arange(100):
first_sample = total_comps.sample(500, with_replacement=False)
medians = bootstrap_median(first_sample, 'Total Compensation', 5000)
left_ends = np.append(left_ends, percentile(2.5, medians))
right_ends = np.append(right_ends, percentile(97.5, medians))
intervals = Table().with_columns(
'Left', left_ends,
'Right', right_ends
)
```
對于 100 個重復中的每個,我們得到了一個中位數估計量的區間。
```py
intervals
```
| Left | Right |
| --- | --- |
| 100547 | 115112 |
| 98788.4 | 112129 |
| 107981 | 121218 |
| 100965 | 114796 |
| 102596 | 112056 |
| 105386 | 113909 |
| 105225 | 116918 |
| 102844 | 116712 |
| 106584 | 118054 |
| 108451 | 118421 |
(省略了 90 行)
良好的區間是那些包含我們試圖估計的參數的區間。 通常參數是未知的,但在本節中,我們碰巧知道參數是什么。
```py
pop_median
110305.78999999999
```
100 個區間中有多少個包含總體中位數? 這是左端低于且右端高于總體中位數的區間數量。
```py
intervals.where('Left', are.below(pop_median)).where('Right', are.above(pop_median)).num_rows
95
```
構建所有區間需要花費幾分鐘時間,但如果你有耐心,請再試一次。最有可能的是,100 個區間中有大約 95 個將是良好的:它們將包含參數。
因為它們有較大的重疊,所以很難在橫軸上顯示所有的區間 - 畢竟,它們都試圖估計相同的參數。下圖通過豎直堆疊,在相同軸域上展示的每個區間。縱軸簡單地是重復的序號,區間從中生成。
紅線是參數所在的位置。良好的區間覆蓋了參數;通常有大約 95 個。
如果一個區間不能覆蓋這個參數,就是個糟糕的事情。在這個地方,你可以看到紅線周圍的“亮光”。他們中只有很少 - 通常是大約 5 個 - 但是他們確實存在。
任何基于抽樣的方法都有可能脫線。基于隨機抽樣的方法的優點是,我們可以量化它們可能脫線的頻率。

為了總結模擬所示的內容,假設你通過以下過程來估計總體中位數:
從總體中隨機抽取一個大樣本。
自舉你的隨機樣本,并從新的隨機樣本中獲取估計量。
重復上述步驟數千次,并獲得數千個估計量。
挑選所有估計量的“中間 95%”的區間。
這給了你一個估計量的區間。現在,如果重復整個過程 100 次,會得到 100 個區間,那么 100 個區間中的大約 95 個將包含總體的參數。
換句話說,95% 的時間內,這個估計過程捕獲了參數。
你可以用一個不同的值代替 95%,只要它不是 100。假設你用 80% 代替了 95%,并保持樣本大小為 500。那么你的估計量的區間將比我們這里的模擬要短,因為“中間 80%”是比“中間 95%”更小的范圍。只有大約 80% 的區間將包含參數。
## 置信區間
我們已經開發了一種方法,通過使用隨機抽樣和自舉來估計參數。我們的方法產生一個估計區間,來解釋隨機樣本的機會變異。通過提供一個估計區間而不是一個估計量,我們給自己一些回旋的余地。
在前面的例子中,我們看到我們的估計過程在 95% 的時間內產生了一個良好的區間,一個“良好”的區間就是包含這個參數的區間。對于這個過程的結果很好,我們說我們有 95% 的置信度(信心)。我們的估計區間稱為參數的 95% 置信區間,95% 稱為區間的置信度。
前一個例子中的情況有點不尋常。因為我們碰巧知道參數的值,所以我們能夠檢查一個區間是好還是不好,這反過來又幫助我們看到,我們的估計過程每 100 次中有 95 次捕獲了參數。
但通常情況下,數據科學家不知道參數的值。這就是他們首先想要估計的原因。在這種情況下,他們通過使用一些方法,類似我們開發的方法,獲得未知參數的估計區間。由于統計理論,和我們所看到的演示,數據科學家可以確信,他們產生區間的過程,會以已知百分比的幾率,產生一個良好的區間。
### 總體中位數的置信區間:自舉百分位數方法
現在我們使用自舉法來估計未知總體的中位數。 數據來自大型醫院系統中的新生兒樣本; 我們將把它看作是一個簡單的隨機樣本,雖然抽樣分多個階段完成。 Deborah Nolan 和 Terry Speed 的 Stat Labs 擁有一個大數據集的詳細信息,這個樣本是從中抽取的。
`baby`表中包含以下母嬰偶對的數量:嬰兒的出生體重(盎司),孕期天數,母親的年齡,母親身高(英寸),孕期體重(磅),母親是否在孕期吸煙。
```py
baby = Table.read_table('baby.csv')
baby
```
| Birth Weight | Gestational Days | Maternal Age | Maternal Height | Maternal Pregnancy Weight | Maternal Smoker |
| --- | --- | --- | --- | --- | --- |
| 120 | 284 | 27 | 62 | 100 | False |
| 113 | 282 | 33 | 64 | 135 | False |
| 128 | 279 | 28 | 64 | 115 | True |
| 108 | 282 | 23 | 67 | 125 | True |
| 136 | 286 | 25 | 62 | 93 | False |
| 138 | 244 | 33 | 62 | 178 | False |
| 132 | 245 | 23 | 65 | 140 | False |
| 120 | 289 | 25 | 62 | 125 | False |
| 143 | 299 | 30 | 66 | 136 | True |
| 140 | 351 | 27 | 68 | 120 | False |
(省略了 1164 行)
出生體重是新生兒健康的一個重要因素 - 較小的嬰兒比較大的嬰兒在初期需要更多的醫療護理。 因此,在嬰兒出生前估計出生體重是有幫助的。 一種方法是檢查出生體重和懷孕天數之間的關系。
這種關系的一個簡單的衡量標準是出生體重與懷孕天數的比值。`ratios`表包含`baby`的前兩列,以及一列`ratios`。 這一列的第一個條目按以下方式計算:
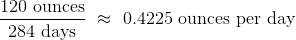
```py
ratios = baby.select('Birth Weight', 'Gestational Days').with_column(
'Ratio BW/GD', baby.column('Birth Weight')/baby.column('Gestational Days')
)
ratios
```
| Birth Weight | Gestational Days | Ratio BW/GD |
| --- | --- | --- | --- |
| 120 | 284 | 0.422535 |
| 113 | 282 | 0.400709 |
| 128 | 279 | 0.458781 |
| 108 | 282 | 0.382979 |
| 136 | 286 | 0.475524 |
| 138 | 244 | 0.565574 |
| 132 | 245 | 0.538776 |
| 120 | 289 | 0.415225 |
| 143 | 299 | 0.478261 |
| 140 | 351 | 0.39886 |
(省略了 1164 行)
```py
ratios.select('Ratio BW/GD').hist()
```

一眼望去,直方圖看起來相當對稱,密度在 4opd 到 4.5opd 的區間內是最大的。 但仔細一看,就可以看出一些比例相當大。 比率的最大值剛好超過 0.78opd,幾乎是通常值的兩倍。
```py
ratios.sort('Ratio BW/GD', descending=True).take(0)
```
| Birth Weight | Gestational Days | Ratio BW/GD |
| --- | --- | --- |
| 116 | 148 | 0.783784 |
中位數提供了通常比例的感覺,因為它不受非常大或非常小的比例的影響。 樣本(比值)的中位數約為 0.429opd。
```py
np.median(ratios.column(2))
0.42907801418439717
```
但是總體中位數是多少? 我們不知道,所以我們會估計它。
我們的方法將與前一節完全相同。 我們將自舉樣本 5000 次,結果是 5000 個中位數的估計量。 我們 95% 的置信區間將是我們所有估計量的“中間 95%”。
回憶前一節定義的`bootstrap_median`函數。 我們將調用這個函數,并構造總體(比值)中位數的 95% 置信區間。請記住,`ratios`表包含來自我們的原始樣本的相關數據。
```py
def bootstrap_median(original_sample, label, replications):
"""Returns an array of bootstrapped sample medians:
original_sample: table containing the original sample
label: label of column containing the variable
replications: number of bootstrap samples
"""
just_one_column = original_sample.select(label)
medians = make_array()
for i in np.arange(replications):
bootstrap_sample = just_one_column.sample()
resampled_median = percentile(50, bootstrap_sample.column(0))
medians = np.append(medians, resampled_median)
return medians
# Generate the medians from 5000 bootstrap samples
bstrap_medians = bootstrap_median(ratios, 'Ratio BW/GD', 5000)
# Get the endpoints of the 95% confidence interval
left = percentile(2.5, bstrap_medians)
right = percentile(97.5, bstrap_medians)
make_array(left, right)
array([ 0.42545455, 0.43262411])
```
95% 置信區間是 0.425opd 到 0.433opd。 我們估計的總體(出生重量與懷孕天數的比值)中位數,在 0.425opd 到 0.433opd 的范圍內。
基于原始樣本的估計量 0.429 恰好在區間兩端的中間,盡管這通常不是真的。
為了使我們的結果可視化,讓我們畫出我們自舉的中位數的經驗直方圖,并將置信區間置于橫軸上。
```py
resampled_medians = Table().with_column(
'Bootstrap Sample Median', bstrap_medians
)
resampled_medians.hist(bins=15)
plots.plot(make_array(left, right), make_array(0, 0), color='yellow', lw=8);
```

這個直方圖和區間就像我們在前一節中繪制的直方圖和區間,只有一個很大的區別 - 沒有顯示參數的紅點。 我們不知道這個點應該在哪里,或者它是否在區間中。
我們只是有一個估計區間。 這是估計量的 95% 置信區間,因為生成它的過程在 95% 的時間中產生了良好的區間。 那肯定是在隨機猜測!
請記住,這個區間是一個大約 95% 的置信區間。 計算中涉及到很多近似值。 近似值并不差,但并不準確。
### 總體均值的置信區間:自舉百分位數方法
我們為中位數所做的事情也可以用于均值。 假設我們想估計總體中的母親的平均年齡。 自然估計量是樣本中的母親的平均年齡。 這是他們的年齡分布,他們的平均年齡大約是 27.2 歲。
```py
baby.select('Maternal Age').hist()
```

```py
np.mean(baby.column('Maternal Age'))
27.228279386712096
```
母親的平均年齡是多少? 我們不知道這個參數的值。
我們用自舉法來估計未知參數。 為此,我們將編輯`bootstrap_median`的代碼,而不是定義函數`bootstrap_mean`。 代碼是相同的,除了統計量是代替中位數的均值,并且收集在一個名為`means`而不是`medians`的數組中。
```py
def bootstrap_mean(original_sample, label, replications):
"""Returns an array of bootstrapped sample means:
original_sample: table containing the original sample
label: label of column containing the variable
replications: number of bootstrap samples
"""
just_one_column = original_sample.select(label)
means = make_array()
for i in np.arange(replications):
bootstrap_sample = just_one_column.sample()
resampled_mean = np.mean(bootstrap_sample.column(0))
means = np.append(means, resampled_mean)
return means
# Generate the means from 5000 bootstrap samples
bstrap_means = bootstrap_mean(baby, 'Maternal Age', 5000)
# Get the endpoints of the 95% confidence interval
left = percentile(2.5, bstrap_means)
right = percentile(97.5, bstrap_means)
make_array(left, right)
array([ 26.89778535, 27.55962521])
```
95% 置信區間是約 26.9 歲到約 27.6 歲。 也就是說,我們估計的母親的平均年齡在 26.9 歲到 27.6 歲之間。
注意兩端距原始樣本均值 27.2 歲的距離。 樣本量非常大 - 1174 個母親 - 所以樣本均值變化不大。 我們將在下一章進一步探討這個觀察。
下面顯示了 5000 個自舉均值的經驗直方圖,以及總體均值的 95% 置信區間。
```py
resampled_means = Table().with_column(
'Bootstrap Sample Mean', bstrap_means
)
resampled_means.hist(bins=15)
plots.plot(make_array(left, right), make_array(0, 0), color='yellow', lw=8);
```

原始樣本的均值(27.23 歲)同樣接近區間中心。 這并不奇怪,因為每個自舉樣本都是從相同的原始樣本中抽取的。 自舉樣本的均值大約對稱分布原始樣本(從其中抽取)的均值的兩側。
還要注意,即使所采樣的年齡的直方圖完全不是對稱的,二次樣本的均值的經驗直方圖也是大致對稱的鐘形:
```py
baby.select('Maternal Age').hist()
```

這是概率統計的中心極限定理的結果。 在后面的章節中,我們將看到這個定理是什么。
### 80% 置信區間
你可以使用自舉法來構建任意水平的置信區間。 例如,要為總體中的平均年齡構建 80% 置信區間,可以選取二次樣本的均值的“中間 80%”。 所以你會希望為兩個尾巴的每一個分配 10%,因此端點是二次樣本的均值的第 10 和第 90 個百分位數。
```py
left_80 = percentile(10, bstrap_means)
right_80 = percentile(90, bstrap_means)
make_array(left_80, right_80)
array([ 27.01192504, 27.439523 ])
resampled_means.hist(bins=15)
plots.plot(make_array(left_80, right_80), make_array(0, 0), color='yellow', lw=8);
```

這個 80% 置信區間比 95% 置信區間要短得多。 它只是約定 27.0 歲到約 27.4 歲。 雖然這是估計量的較窄區間,你知道這個過程在 80% 的時間內產生良好的區間。
之前過程產生了較寬的區間,但是我們對產生它的過程擁有更高的置信度。
為了以較高的置信度獲得較窄的置信區間,你必須從較大的樣本開始。 我們將在下一章看到為什么。
### 總體比例的置信區間:自舉百分位數方法
在樣本中,39% 的母親在懷孕期間吸煙。
```py
baby.where('Maternal Smoker', are.equal_to(True)).num_rows/baby.num_rows
0.3909710391822828
```
以下對觀察很實用,這個比例也可以通過數組操作來計算:
```py
smoking = baby.column('Maternal Smoker')
np.count_nonzero(smoking)/len(smoking)
0.3909710391822828
```
> 譯者注:
> `np.count_nonzero(arr)`等價于`np.sum(arr != 0)`。
總體中有百分之多少的母親在懷孕期間吸煙? 這是一個未知的參數,我們可以通過自舉置信區間來估計。 這個過程中的步驟與我們用來估計總體均值和中位數的步驟相似。
我們將首先定義一個函數`bootstrap_proportion`,返回一個自舉樣本的比例的數組。 我們再一次通過編輯`bootstrap_median`的定義來實現它。 計算中唯一的變化是用二次樣本的吸煙者比例代替中位數。 該代碼假定數據列由布爾值組成。 其他的改變只是數組的名字,來幫助我們閱讀和理解我們的代碼。
```py
def bootstrap_proportion(original_sample, label, replications):
"""Returns an array of bootstrapped sample proportions:
original_sample: table containing the original sample
label: label of column containing the Boolean variable
replications: number of bootstrap samples
"""
just_one_column = original_sample.select(label)
proportions = make_array()
for i in np.arange(replications):
bootstrap_sample = just_one_column.sample()
resample_array = bootstrap_sample.column(0)
resampled_proportion = np.count_nonzero(resample_array)/len(resample_array)
proportions = np.append(proportions, resampled_proportion)
return proportions
```
讓我們使用`bootstrap_proportion`來構建總體的母親吸煙者百分比的 95% 置信區間。 該代碼類似于均值和中位數的相應代碼。
```py
# Generate the proportions from 5000 bootstrap samples
bstrap_props = bootstrap_proportion(baby, 'Maternal Smoker', 5000)
# Get the endpoints of the 95% confidence interval
left = percentile(2.5, bstrap_props)
right = percentile(97.5, bstrap_props)
make_array(left, right)
array([ 0.36286201, 0.41908007])
```
置信區間是 36% 到 42%。原始樣本的百分比 39% 非常接近于區間的中心。你可以在下面看到:
```py
resampled_proportions = Table().with_column(
'Bootstrap Sample Proportion', bstrap_props
)
resampled_proportions.hist(bins=15)
plots.plot(make_array(left, right), make_array(0, 0), color='yellow', lw=8);
```

### 自舉法的注意事項
自舉法是一個優雅而強大的方法。在使用之前,記住一些要點非常重要。
以大型隨機樣本開始。如果你不這樣做,該方法可能無法正常工作。它的成功基于大型隨機樣本(因此也從樣本中重采樣)。平均定律說,如果隨機樣本很大,這很可能是真的。
為了近似統計量的概率分布,最好多次復制重采樣過程。數千次重復將產生樣本中位數分布的正確近似,特別是如果總體分布存在峰值并且不是非常不對稱的話。在我們的例子中,我們使用了 5000 次重復,但一般會推薦 10000 次。
自舉百分位數方法適用于基于大型隨機樣本,估計總體中位數或均值。但是,它也有其局限性,所有的估計方法也是如此。例如,在以下情況下,它預期沒有效果。
+ 目標是估計總體中的最小值或最大值,或非常低或非常高的百分位數,或受總體中稀有元素影響較大的參數。
+ 統計量的概率分布不是近似鐘形的。
+ 原始樣本非常小,比如 10 或 15。
## 使用置信區間
```py
def bootstrap_median(original_sample, label, replications):
"""Returns an array of bootstrapped sample medians:
original_sample: table containing the original sample
label: label of column containing the variable
replications: number of bootstrap samples
"""
just_one_column = original_sample.select(label)
medians = make_array()
for i in np.arange(replications):
bootstrap_sample = just_one_column.sample()
resampled_median = percentile(50, bootstrap_sample.column(0))
medians = np.append(medians, resampled_median)
return medians
def bootstrap_mean(original_sample, label, replications):
"""Returns an array of bootstrapped sample means:
original_sample: table containing the original sample
label: label of column containing the variable
replications: number of bootstrap samples
"""
just_one_column = original_sample.select(label)
means = make_array()
for i in np.arange(replications):
bootstrap_sample = just_one_column.sample()
resampled_mean = np.mean(bootstrap_sample.column(0))
means = np.append(means, resampled_mean)
return means
def bootstrap_proportion(original_sample, label, replications):
"""Returns an array of bootstrapped sample proportions:
original_sample: table containing the original sample
label: label of column containing the Boolean variable
replications: number of bootstrap samples
"""
just_one_column = original_sample.select(label)
proportions = make_array()
for i in np.arange(replications):
bootstrap_sample = just_one_column.sample()
resample_array = bootstrap_sample.column(0)
resampled_proportion = np.count_nonzero(resample_array)/len(resample_array)
proportions = np.append(proportions, resampled_proportion)
return proportions
```
置信區間只有一個目的 - 根據隨機樣本中的數據估計未知參數。在最后一節中,我們說區間`(36%, 42%)`是總體中吸煙者百分比的約 95% 的置信區間。正式的表述方式為,據我們估計,總體中的吸煙者比例在 36% 到 42% 之間,我們的估計過程在 95% 的時間內是正確的。
克制住將置信區間用于其他目的的沖動,這很重要。例如,回想一下,我們計算了區間`(26.9 yr, 27.6 yr)`,作為母親平均年齡的約 95% 的置信區間。區間的一個令人驚訝的常見誤用是得出這樣的結論,約 95% 的女性在 26.9 歲至 27.6 歲之間。你不需要怎么了解置信區間,來查看這是不是正確的 - 你不會預計 95% 的母親的年齡在這個較小的范圍內。實際上,抽樣年齡的直方圖顯示出相當多的變化。
```py
baby = Table.read_table('baby.csv')
baby.select('Maternal Age').hist()
```

抽樣年齡的一小部分在`(26.9, 27.6)`的區間內,你可能會預計總體中的百分比很小。 區間只是估計一個數字:總體中所有年齡的平均值。
但是,除了僅僅告訴我們這個參數有多大之外,用置信區間來估計一個參數確實有重要的用處。
### 使用置信區間來檢驗假設
我們總體(年齡)均值的 95% 置信區間是 26.9 歲到 27.6 歲。假設有人想要測試以下假設:
原假設。人口的平均年齡是 30 歲。
備選假設。人口的平均年齡不是 30 歲。
那么,如果你使用 5% 的截斷值作為 P 值,則會拒絕原假設。這是因為總體平均值 30 不在 95% 置信區間內。在 5% 的顯著性水平上,30 對于人口平均值并不合理。
置信區間的使用是置信區間和檢驗之間二元性結果:如果你正在測試總體平均值是否是特定值 x,并且你使用的 5% 截斷值作為 P 值,那么如果 x 不在平均值的 95% 置信區間內,你將拒絕原零假設。
這可以由統計理論來確定。在實踐中,它只是歸結為,檢查原假設中指定的值是否在置信區間內。
如果你使用 1% 的截斷值作為 P 值,你必須檢查,原假設中指定的值是否在總體均值的 99% 置信區間內。
粗略地說,如果樣本量很大,這些陳述也適用于總體比例。
雖然我們現在有一種方法,使用置信區間來檢驗一種特定假設,但是你可能想知道,測試總體(年齡)的均值是否等于 30 的意義。實際上,這個意義并不清楚。但是在某些情況下,對這種假設的檢驗既自然又有用。
我們將在數據的背景下來研究它,這些數據是霍奇金病治療的隨機對照試驗中收集的信息的子集。霍奇金病是一種通常影響年輕人的癌癥。這種疾病是可以治愈的,但治療可能非常艱難。該試驗的目的是找出治療癌癥的劑量,并且將對患者的不利影響最小化。
這張表格包含治療對 22 名患者肺部的影響的數據。這些列是:
+ 身高(厘米)
+ 覆蓋物輻射的測量(頸部,胸部,手臂下)
+ 化療的測量
+ 基線下,即在治療開始時的肺健康得分;較高的分數對應于更健康的肺
+ 治療后 15 個月,相同的肺的健康得分
```py
hodgkins = Table.read_table('hodgkins.csv')
hodgkins
```
| height | rad | chemo | base | month15 |
| --- | --- | --- | --- | --- |
| 164 | 679 | 180 | 160.57 | 87.77 |
| 168 | 311 | 180 | 98.24 | 67.62 |
| 173 | 388 | 239 | 129.04 | 133.33 |
| 157 | 370 | 168 | 85.41 | 81.28 |
| 160 | 468 | 151 | 67.94 | 79.26 |
| 170 | 341 | 96 | 150.51 | 80.97 |
| 163 | 453 | 134 | 129.88 | 69.24 |
| 175 | 529 | 264 | 87.45 | 56.48 |
| 185 | 392 | 240 | 149.84 | 106.99 |
| 178 | 479 | 216 | 92.24 | 73.43 |
(省略了 12 行)
我們將比較基準和 15 個月的得分。 由于每行對應一個病人,我們說基線得分的樣本和 15 個月得分的樣本是成對的 - 它們不是每組 22 個值的兩組,而是 22 對值,每個病人一個。
一眼望去,你可以看到,15 個月的得分往往低于基線得分 - 抽樣患者的肺似乎在治療后 15 個月更差。 這個由`drop`列主要是正值來證實,它是基線得分減去 15 個月的得分。
```py
hodgkins = hodgkins.with_column(
'drop', hodgkins.column('base') - hodgkins.column('month15')
)
hodgkins
```

| height | rad | chemo | base | month15 | drop |
| --- | --- | --- | --- | --- | --- |
| 164 | 679 | 180 | 160.57 | 87.77 | 72.8 |
| 168 | 311 | 180 | 98.24 | 67.62 | 30.62 |
| 173 | 388 | 239 | 129.04 | 133.33 | -4.29 |
| 157 | 370 | 168 | 85.41 | 81.28 | 4.13 |
| 160 | 468 | 151 | 67.94 | 79.26 | -11.32 |
| 170 | 341 | 96 | 150.51 | 80.97 | 69.54 |
| 163 | 453 | 134 | 129.88 | 69.24 | 60.64 |
| 175 | 529 | 264 | 87.45 | 56.48 | 30.97 |
| 185 | 392 | 240 | 149.84 | 106.99 | 42.85 |
| 178 | 479 | 216 | 92.24 | 73.43 | 18.81 |
(省略了 12 行)
```py
hodgkins.select('drop').hist(bins=np.arange(-20, 81, 20))
```
```py
np.mean(hodgkins.column('drop'))
28.615909090909096
```
但是,這可能是機會變異的結果嗎? 似乎并不如此,但數據來自隨機樣本。 難道在整個人群中,平均下降值只有 0 嗎?
為了回答這個問題,我們可以設定兩個假設:
原假設:總體(下降值)均值為 0。
備選假設:總體(下降值)均值不為 0。
為了使用 1% 的截斷值作為 P 值來驗證這個假設,讓我們為總體(下降值)均值構建近似 99% 置信區間。
```py
bstrap_means = bootstrap_mean(hodgkins, 'drop', 10000)
left = percentile(0.5, bstrap_means)
right = percentile(99.5, bstrap_means)
make_array(left, right)
array([ 17.25045455, 40.60136364])
resampled_means = Table().with_column(
'Bootstrap Sample Mean', bstrap_means
)
resampled_means.hist()
plots.plot(make_array(left, right), make_array(0, 0), color='yellow', lw=8);
```

總體均值的 99% 置信區間是約 17 到約 40。區間不包含 0。因此,我們拒絕原假設。
但是請注意,我們所做的不僅僅是簡單得出結論:總體均值不是 0,我們估計了均值的幅度是多大。這比僅僅說“不是 0”更有用。
對于準確性的注解:我們的置信區間相當寬泛,主要有兩個原因:
+ 置信水平很高(99%)。
+ 與我們之前的例子相比,樣本量相對較小。
在下一章中,我們將研究樣本大小如何影響準確性。我們還將研究,樣本均值的經驗分布為何經常出現鐘形,盡管底層數據的分布根本不是鐘形的。
### 尾注
一個領域的術語通常來自該領域的主要研究人員。首先提出自舉技術的 [Brad Efron](https://en.wikipedia.org/wiki/Bradley_Efron) 用了一個[美國血統的術語](https://en.wikipedia.org/wiki/Bootstrapping)。中國統計學家不甘示弱,[提出了自己的方法](http://econpapers.repec.org/article/eeestapro/v_3a37_3ay_3a1998_3ai_3a4_3ap_3a321-329.htm)。
