# 九、經驗分布 > 原文：[Empirical Distributions](https://github.com/data-8/textbook/tree/gh-pages/chapters/09) > 譯者：[飛龍](https://github.com/wizardforcel) > 協議：[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 大部分數據科學都涉及來自大型隨機樣本的數據。 在本節中，我們將研究這些樣本的一些屬性。 我們將從一個簡單的實驗開始：多次擲骰子并跟蹤出現的點數。 `die `表包含骰子面上的點數。 所有的數字只出現一次，因為我們假設骰子是平等的。 ```py die = Table().with_column('Face', np.arange(1, 7, 1)) die ``` | Face | | --- | | 1 | | 2 | | 3 | | 4 | | 5 | | 6 | ### 概率分布 下面的直方圖幫助我們可視化，每個面出現概率為 1/6 事實。 我們說直方圖顯示了所有可能的面的概率分布。 由于所有的條形表示相同的百分比幾率，所以這個分布成為整數 1 到 6 上的均勻分布。 ```py die_bins = np.arange(0.5, 6.6, 1) die.hist(bins = die_bins) ```  遞增值由相同的固定量分隔，例如骰子面上的值（遞增值由 1 分隔），這樣的變量被稱為離散值。上面的直方圖被稱為離散直方圖。它的桶由數組`die_bins`指定，并確保每個條形的中心是對應的整數值。 重要的是要記住，骰子不能顯示 1.3 個點或 5.2 個點 - 總是顯示整數個點。但是我們的可視化將每個值的概率擴展到條形區域。雖然在本課程的這個階段這看起來有些隨意，但是稍后當我們在離散直方圖上疊加平滑曲線時，這將變得很重要。 在繼續之前，讓我們確保軸域上的數字是有意義的。每個面的概率是 1/6，四舍五入到小數點后兩位的概率是 16.67%。每個桶的寬度是 1 個單位。所以每個條形的高度是每單位 16.67%。這與圖形的水平和垂直比例一致。 ### 經驗分布 上面的分布由每個面的理論概率組成。 這不基于數據。 不投擲任何骰子，它就可以被研究和理解。 另一方面，經驗分布是觀測數據的分布。 他們可以通過經驗直方圖可視化。 讓我們通過模擬一個骰子的投擲來獲得一些數據。 這可以通過 1 到 6 的整數的帶放回隨機抽樣來完成。為了使用 Python 來實現，我們將使用`Table`的`sample`方法，它帶放回地隨機抽取表中的行。它的參數是樣本量，它返回一個由選定的行組成的表。 `with_replacement=False`的可選參數指定了應該抽取樣本而不放回，但不適用于投擲骰子。 這是一個十次骰子投擲的結果。 ```py die.sample(10) ``` | Face | | --- | | 5 | | 3 | | 3 | | 4 | | 2 | | 2 | | 4 | | 1 | | 6 | | 6 | 我們可以使用相同的方法來模擬盡可能多的投擲，然后繪制結果的經驗直方圖。 因為我們要反復這樣做，所以我們定義了一個函數`empirical_hist_die`，它以樣本量為參數；該函數根據其參數多次投擲骰子，然后繪制直方圖。 ```py def empirical_hist_die(n): die.sample(n).hist(bins = die_bins) ``` ### 經驗直方圖 這是十次投擲的經驗直方圖。 它看起來不像上面的概率直方圖。 運行該單元格幾次，看看它如何變化。 ```py empirical_hist_die(10) ```  當樣本量增加時，經驗直方圖開始看起來更像是理論概率的直方圖。 ```py empirical_hist_die(100) ```  ```py empirical_hist_die(1000) ```  當我們增加模擬中的投擲次數時，每個條形的面積接近 16.67%，這是概率直方圖中每個條形的面積。 我們在實例中觀察到了一般規則： ### 平均定律 如果偶然的實驗在相同的條件下獨立重復，那么從長遠來看，事件發生的頻率越來越接近事件的理論概率。 例如，從長遠來看，四點的比例越來越接近 1/6。 這里“獨立地且在相同的條件下”意味著，無論所有其他重復的結果如何，每個重復都以相同的方式執行。 ## 從總體中取樣 當隨機樣本來自較大總體時，平均定律也成立。 作為一個例子，我們將研究航班延誤時間的總體。 `united `表包含 2015 年夏天從舊金山出發的美聯航國內航班的數據。數據由[美國運輸部運輸統計局](http://www.transtats.bts.gov/Fields.asp?Table_ID=293)公布。 這里有 13,825 行，每行對應一個航班。 列是航班日期，航班號，目的地機場代碼和以分鐘為單位的出發延誤時間。有些延誤時間是負的；那些航班提前離開。 ```py united = Table.read_table('united_summer2015.csv') united ``` | Date | Flight Number | Destination | Delay | | --- | --- | --- | --- | | 6/1/15 | 73 | HNL | 257 | | 6/1/15 | 217 | EWR | 28 | | 6/1/15 | 237 | STL | -3 | | 6/1/15 | 250 | SAN | 0 | | 6/1/15 | 267 | PHL | 64 | | 6/1/15 | 273 | SEA | -6 | | 6/1/15 | 278 | SEA | -8 | | 6/1/15 | 292 | EWR | 12 | | 6/1/15 | 300 | HNL | 20 | | 6/1/15 | 317 | IND | -10 | （省略了 13815 行） 一個航班提前 16 分鐘起飛，另一個航班延誤 580 分鐘。 其他延遲時間幾乎都在 -10 分鐘到 200 分鐘之間，如下面的直方圖所示。 ```py united.column('Delay').min() -16 united.column('Delay').max() 580 delay_bins = np.append(np.arange(-20, 301, 10), 600) united.select('Delay').hist(bins = delay_bins, unit = 'minute') ```  就本節而言，僅僅關注部分數據就足夠了，我們忽略延遲超過 200 分鐘的 0.8% 的航班。 這個限制只是為了視覺便利。 該表仍然保留所有的數據。 ```py united.where('Delay', are.above(200)).num_rows/united.num_rows 0.008390596745027125 delay_bins = np.arange(-20, 201, 10) united.select('Delay').hist(bins = delay_bins, unit = 'minute') ```  `[0,10)`的條形高度不到每分鐘 3%，這意味著只有不到 30% 的航班延誤了 0 到 10 分鐘。 這是通過行的計數來確認的： ```py united.where('Delay', are.between(0, 10)).num_rows/united.num_rows 0.2935985533453888 ``` ### 樣本的經驗分布 現在讓我們將這 13,825 個航班看做一個總體，并從中帶放回地抽取隨機樣本。 將我們的分析代碼打包成一個函數是有幫助的。 函數`empirical_hist_delay`以樣本量為參數，繪制結果的經驗直方圖。 ```py def empirical_hist_delay(n): united.sample(n).select('Delay').hist(bins = delay_bins, unit = 'minute') ``` 正如我們用骰子所看到的，隨著樣本量的增加，樣本的經驗直方圖更接近于總體的直方圖。 將這些直方圖與上面的總體直方圖進行比較。 ```py empirical_hist_delay(10) ```  ```py empirical_hist_delay(100) ```  最一致的可見差異在總體中罕見的值之中。 在我們的示例中，這些值位于分布的最右邊。 但隨著樣本量的增加，這些值以大致正確的比例，開始出現在樣本中。 ```py empirical_hist_delay(1000) ```  ### 樣本的經驗直方圖的總結 我們在本節中觀察到的東西，可以總結如下： 對于大型隨機樣本，樣本的經驗直方圖類似于總體的直方圖，概率很高。 這證明了，在統計推斷中使用大型隨機樣本是合理的。 這個想法是，由于大型隨機樣本可能類似于從中抽取的總體，從樣本中計算出的數量可能接近于總體中相應的數量。 ## 輪盤賭 上面的分布讓我們對整個隨機樣本有了印象。但有時候我們只是對基于樣本計算的一個或兩個量感興趣。 例如，假設樣本包含一系列投注的輸贏。那么我們可能只是對贏得的總金額感興趣，而不是輸贏的整個序列。 使用我們的幾率長期行為的新知識，讓我們探索賭博游戲。我們將模擬輪盤賭，它在拉斯維加斯和蒙特卡洛等賭場中受歡迎。 在內華達，輪盤賭的主要隨機器是一個帶有 38 個口袋的輪子。其中兩個口袋是綠色的，十八個黑色，十八個紅色。輪子在主軸上，輪子上有一個小球。當輪子旋轉時，球體跳起來，最后落在其中一個口袋里。這就是獲勝的口袋。 `wheel`表代表內華達輪盤賭的口袋。 ```py wheel ``` | Pocket | Color | | --- | --- | | 0 | green | | 00 | green | | 1 | red | | 2 | black | | 3 | red | | 4 | black | | 5 | red | | 6 | black | | 7 | red | | 8 | black | （省略了 28 行） 你可以對輪盤賭桌上展示的幾個預先指定的口袋下注。 如果你對“紅色”下注，如果球落在紅色的口袋里，你就贏了。 紅色的下注返回相等的錢。 也就是說，它支付一比一。為了理解這是什么意思，假設你在“紅色”下注一美元。 第一件事情發生之前，即使在車輪旋轉之前，你必須交出你的一美元。 如果球落在綠色或黑色的口袋里，你就失去它了。 如果球落在紅色的口袋里，你會把你的錢拿回來（讓你不輸不贏），再加上另外一美元的獎金。 函數`red_winnings`以一個顏色作為參數，如果顏色是紅色，則返回`1`。 對于所有其他顏色，它返回`-1`。 我們將`red_winnings`應用于`wheel`的`Color`列，來獲得新的表`bets`，如果你對紅色下注一美元，它顯示每個口袋的凈收益。 ```py def red_winnings(color): if color == 'red': return 1 else: return -1 bets = wheel.with_column( 'Winnings: Red', wheel.apply(red_winnings, 'Color') ) bets ``` | Pocket | Color | Winnings: Red | | --- | --- | --- | | 0 | green | -1 | | 00 | green | -1 | | 1 | red | 1 | | 2 | black | -1 | | 3 | red | 1 | | 4 | black | -1 | | 5 | red | 1 | | 6 | black | -1 | | 7 | red | 1 | | 8 | black | -1 | （省略了 28 行） 假設我們決定對紅色下注一美元，會發生什么呢？ 這里是一輪的模擬。 ```py one_spin = bets.sample(1) one_spin ``` | Pocket | Color | Winnings: Red | | --- | --- | --- | | 14 | red | 1 | 這輪的顏色是`Color`列中的值。 無論你的賭注如何，結果可能是紅色，綠色或黑色。 要看看這些事件發生的頻率，我們可以模擬許多這樣的單獨輪次，并繪制出我們所看到的顏色的條形圖。 （我們可以稱之為經驗條形圖。） 為了實現它，我們可以使用`for`循環。 我們在這里選擇了重復 5000 次，但是當你運行這個單元格時，你可以改變它。 ```py num_simulations = 5000 colors = make_array() winnings_on_red = make_array() for i in np.arange(num_simulations): spin = bets.sample(1) new_color = spin.column("Color").item(0) colors = np.append(colors, new_color) new_winnings = spin.column('Winnings: Red') winnings_on_red = np.append(winnings_on_red, new_winnings) Table().with_column('Color', colors)\ .group('Color')\ .barh('Color') ```  38 個口袋里有 18 個是紅色的，每個口袋都是等可能的。 因此，在 5000 次模擬中，我們預計大致（但可能不是完全）看到`18/38*5000`或者 2,368 次紅色。模擬證明了這一點。 在模擬中，我們也記錄了你的獎金。 這些經驗直方圖顯示了，你對紅色下注的不同結果的（近似）幾率。 ```py Table().with_column('Winnings: Red', winnings_on_red)\ .hist(bins = np.arange(-1.55, 1.65, .1)) ```  每個模擬的唯一可能的結果是，你贏了一美元或輸了一美元，這反映在直方圖中。 我們也可以看到，你贏的次數要比輸的次數少一點。 你喜歡這個賭博策略嗎？ ### 多次游戲 大多數輪盤賭玩家玩好幾輪。 假設你在 200 次獨立輪次反復下注一美元。 你總共會賺多少錢？ 這里是一套 200 輪的模擬。 `spins`表包括所有 200 個賭注的結果。 你的凈收益是`Winnings: Red`列中所有 +1 和 -1 的和。 ```py spins = bets.sample(200) spins.column('Winnings: Red').sum() -26 ``` 運行幾次單元格。 有時你的凈收益是正的，但更多的時候它似乎是負的。 為了更清楚地看到發生了什么，讓我們多次模擬 200 輪，就像我們模擬一輪那樣。 對于每次模擬，我們將記錄來自 200 輪的總獎金。 然后我們將制作 5000 個不同的模擬總獎金的直方圖。 ```py num_spins = 200 net_gain = make_array() for i in np.arange(num_simulations): spins = bets.sample(num_spins) new_net_gain = spins.column('Winnings: Red').sum() net_gain = np.append(net_gain, new_net_gain) Table().with_column('Net Gain on Red', net_gain).hist() ```  注意橫軸上 0 的位置。 這就是你不賺不賠的地方。 通過使用這個賭博策略，你喜歡這個賺錢幾率嗎？ 如果對紅色下注不吸引人，也許值得嘗試不同的賭注。 “分割”（Split）是輪盤賭桌上兩個相鄰號碼的下注，例如 0 和 00。分割的回報是 17 比 1。 `split_winnings`函數將口袋作為參數，如果口袋是 0 或 00，則返回 17。對于所有其他口袋，返回 -1。 表格`more_bets`是投注表格的一個版本，擴展的一列是對 0/00 分割下注的情況下，每個口袋的獎金。 ```py def split_winnings(pocket): if pocket == '0': return 17 elif pocket == '00': return 17 else: return -1 more_bets = wheel.with_columns( 'Winnings: Red', wheel.apply(red_winnings, 'Color'), 'Winnings: Split', wheel.apply(split_winnings, 'Pocket') ) more_bets ``` | Pocket | Color | Winnings: Red | Winnings: Split | | --- | --- | --- | --- | | 0 | green | -1 | 17 | | 00 | green | -1 | 17 | | 1 | red | 1 | -1 | | 2 | black | -1 | -1 | | 3 | red | 1 | -1 | | 4 | black | -1 | -1 | | 5 | red | 1 | -1 | | 6 | black | -1 | -1 | | 7 | red | 1 | -1 | | 8 | black | -1 | -1 | （省略了 28 行） 下面的代碼模擬了兩個投注的結果 - 紅色和 0/00 分割 - 在 200 輪中。 代碼與以前的模擬相同，除了添加了 Split。 （注意：`num_simulations`和`num_spins`之前分別定義為 5,000 和 200，所以我們不需要再次定義它們。） ```py net_gain_red = make_array() net_gain_split = make_array() for i in np.arange(num_simulations): spins = more_bets.sample(num_spins) new_net_gain_red = spins.column('Winnings: Red').sum() net_gain_red = np.append(net_gain_red, new_net_gain_red) new_net_gain_split = spins.column('Winnings: Split').sum() net_gain_split = np.append(net_gain_split, new_net_gain_split) Table().with_columns( 'Net Gain on Red', net_gain_red, 'Net Gain on Split', net_gain_split ).hist(bins=np.arange(-200, 200, 20)) ```  橫軸上 0 的位置表明，無論你選擇哪種賭注，你都更有可能賠錢而不是賺錢。在兩個直方圖中，不到 50% 的區域在 0 的右側。 然而，分割的賭注賺錢幾率更大，賺取超過 50 美元的機會也是如此。 金色直方圖有很多區域在五十美元的右側，而藍色直方圖幾乎沒有。 那么你應該對分割下注嗎？ 這取決于你愿意承擔多少風險，因為直方圖還表明，如果你對分割下注，你比對紅色下注更容易損失超過 50 美元。 輪盤賭桌上，所有賭注的單位美元的預期凈損失相同（除了線注，這是更糟的）。 但一些賭注的回報比其他賭注更為可變。 你可以選擇這些賭注，只要你準備好可能會大輸一場。 ## 統計量的經驗分布 平均定律意味著，大型隨機樣本的經驗分布類似于總體的分布，概率相當高。 在兩個直方圖中可以看到相似之處：大型隨機樣本的經驗直方圖很可能類似于總體的直方圖。 提醒一下，這里是所有美聯航航班延誤的直方圖，以及這些航班的大小為 1000 的隨機樣本的經驗直方圖。 ```py united = Table.read_table('united_summer2015.csv') delay_bins = np.arange(-20, 201, 10) united.select('Delay').hist(bins = delay_bins, unit = 'minute') plots.title('Population'); ```  ```py sample_1000 = united.sample(1000) sample_1000.select('Delay').hist(bins = delay_bins, unit = 'minute') plots.title('Sample of Size 1000'); ```  兩個直方圖明顯相似，雖然他們并不等價。 ### 參數 我們經常對總體相關的數量感興趣。 在選民的總體中，有多少人會投票給候選人 A 呢？ 在 Facebook 用戶的總體中，用戶最多擁有的 Facebook 好友數是多少？ 在美聯航航班的總體中，起飛延誤時間的中位數是多少？ 與總體相關的數量被稱為參數。 對于美聯航航班的總體，我們知道參數“延誤時間的中位數”的值： ```py np.median(united.column('Delay')) 2.0 ``` NumPy 函數`median`返回數組的中值（中位數）。 在所有的航班中，延誤時間的中位數為 2 分鐘。 也就是說，總體中約有 50% 的航班延誤了 2 分鐘以內： ```py united.where('Delay', are.below_or_equal_to(2)).num_rows/united.num_rows 0.5018444846292948 ``` 一半的航班在預定起飛時間的 2 分鐘之內起飛。 這是非常短暫的延誤！ 注意。 由于“重復”，百分比并不完全是 50，也就是說，延誤了 2 分鐘的航班有 480 個。數據集中的重復很常見，我們不會在這個課程中擔心它。 ```py united.where('Delay', are.equal_to(2)).num_rows 480 ``` ### 統計 在很多情況下，我們會感興趣的是找出未知參數的值。 為此，我們將依賴來自總體的大型隨機樣本的數據。 統計量（注意是單數！）是使用樣本中數據計算的任何數字。 因此，樣本中位數是一個統計量。 請記住，`sample_1000`包含來自`united`的 1000 個航班的隨機樣本。 樣本中位數的觀測值是： ```py np.median(sample_1000.column('Delay')) 2.0 ``` 我們的樣本 - 一千個航班 - 給了我們統計量的觀測值。 這提出了一個重要的推論問題： 統計量的數值可能會有所不同。 使用基于隨機樣本的任何統計量時，首先考慮的事情是，樣本可能不同，因此統計量也可能不同。 ```py np.median(united.sample(1000).column('Delay')) 3.0 ``` 運行單元格幾次來查看答案的變化。 通常它等于 2，與總體參數值相同。 但有時候不一樣。 統計量有多么不同？ 回答這個問題的一種方法是多次運行單元格，并記下這些值。 這些值的直方圖將告訴我們統計量的分布。 我們將使用`for`循環來“多次運行單元格”。 在此之前，讓我們注意模擬中的主要步驟。 ### 模擬統計量 我們將使用以下步驟來模擬樣本中位數。 你可以用任何其他樣本量來替換 1000 的樣本量，并將樣本中位數替換為其他統計量。 第一步：生成一個統計量。 抽取大小為 1000 的隨機樣本，并計算樣本的中位數。 注意中位數的值。 第二步：生成更多的統計值。 重復步驟 1 多次，每次重新抽樣。 第三步：結果可視化。 在第二步結束時，你將會記錄許多樣本中位數，每個中位數來自不同的樣本。 你可以在表格中顯示所有的中位數。 你也可以使用直方圖來顯示它們 - 這是統計量的經驗直方圖。 我們現在執行這個計劃。 正如在所有的模擬中，我們首先創建一個空數組，我們在其中收集我們的結果。 + 上面的第一步是`for`循環的主體。 + 第二步，重復第一步“無數次”，由循環完成。 我們“無數次”是5000次，但是你可以改變這個。 + 第三步是顯示表格，并在后面的單元格中調用`hist`。 該單元格需要大量的時間來運行。 那是因為它正在執行抽取大小為 1000 的樣本，并計算其中位數的過程，重復 5000 次。 這是很多抽樣和重復！ ```py medians = make_array() for i in np.arange(5000): new_median = np.median(united.sample(1000).column('Delay')) medians = np.append(medians, new_median) Table().with_column('Sample Median', medians) ``` | Sample Median | | --- | | 3 | | 2 | | 2 | | 3 | | 2 | | 2 | | 2 | | 3 | | 1 | | 3 | （省略了 4990 行） ```py Table().with_column('Sample Median', medians).hist(bins=np.arange(0.5, 5, 1)) ```  你可以看到樣本中位數很可能接近 2，這是總體中位數的值。 由于 1000 次航班延誤的樣本可能與延誤總體相似，因此這些樣本的延誤中位數應接近總體的延誤中位數，也就不足為奇了。 這是一個例子，統計量如何較好估計參數。 ### 模擬的威力 如果我們能夠生成所有可能的大小為 1000 的隨機樣本，我們就可以知道所有可能的統計量（樣本中位數），以及所有這些值的概率。我們可以在統計量的概率直方圖中可視化所有值和概率。 但在許多情況下（包括這個），所有可能的樣本數量足以超過計算機的容量，概率的純粹數學計算可能有些困難。 這是經驗直方圖的作用。 我們知道，如果樣本量很大，并且如果重復抽樣過程無數次，那么根據平均定律，統計量的經驗直方圖可能類似于統計量的概率直方圖。 這意味著反復模擬隨機過程是一種近似概率分布的方法，不需要在數學上計算概率，或者生成所有可能的隨機樣本。因此，計算機模擬成為數據科學中的一個強大工具。他們可以幫助數據科學家理解隨機數量的特性，這些數據會以其他方式進行分析。 這就是這種的模擬的經典例子。 ### 估計敵軍飛機的數量 在第二次世界大戰中，為盟軍工作的數據分析師負責估算德國戰機的數量。 這些數據包括盟軍觀察到的德國飛機的序列號。 這些序列號為數據分析師提供了答案。 為了估算戰機總數，數據分析人員必須對序列號做出一些假設。 這里有兩個這樣的假設，大大簡化，使我們的計算更容易。 + 戰機有`N`架，編號為 `1,2, ..., N`。 + 觀察到的飛機從`N`架飛機中均勻、隨機帶放回地抽取。 目標是估計數字`N`。 這是未知的參數。 假設你觀察一些飛機并記下他們的序列號。 你如何使用這些數據來猜測`N`的值？ 用于估計的自然和簡單的統計量，就是觀察到的最大的序列號。 讓我們看看這個統計量如何用于估計。 但首先是另一個簡化：現在一些歷史學家估計，德國的飛機制造業生產了近 10 萬架不同類型的戰機，但在這里我們只能想象一種。 這使得假設 1 更易于證明。 假設實際上有`N = 300 `個這樣的飛機，而且你觀察到其中的 30 架。 我們可以構造一個名為`serialno`的表，其中包含序列號`1`到`N`。 然后，我們可以帶放回取樣 30 次（見假設 2），來獲得我們的序列號樣本。 我們的統計量是這 30 個數字中的最大值。 這就是我們用來估計參數`N`的東西。 ```py N = 300 serialno = Table().with_column('serial Number', np.arange(1, N+1)) serialno ``` | serial number | | --- | | 1 | | 2 | | 3 | | 4 | | 5 | | 6 | | 7 | | 8 | | 9 | | 10 | （省略了 290 行） ```py serialno.sample(30).column(0).max() 291 ``` 與所有涉及隨機抽樣的代碼一樣，運行該單元幾次；來查看變化。你會發現，即使只有 300 個觀測值，最大的序列號通常在 250-300 范圍內。 原則上，最大的序列號可以像 1 那樣小，如果你不幸看到了 30 次 1 號機。如果你至少觀察到一次 300 號機，它可能會增大到 300。但通常情況下，它似乎處于非常高的 200 以上。看起來，如果你使用最大的觀測序列號作為你對總數的估計，你不會有太大的錯誤。 ### 模擬統計 讓我們模擬統計，看看我們能否證實它。模擬的步驟是： 第一步。從 1 到 300 帶放回地隨機抽樣 30 次，并注意觀察到的最大數量。這是統計量。 第二步。重復步驟一 750 次，每次重新取樣。你可以用任何其他的大數值代替 750。 第三步。創建一個表格來顯示統計量的 750 個觀察值，并使用這些值繪制統計量的經驗直方圖。 ```py sample_size = 30 repetitions = 750 maxes = make_array() for i in np.arange(repetitions): sampled_numbers = serialno.sample(sample_size) maxes = np.append(maxes, sampled_numbers.column(0).max()) Table().with_column('Max Serial Number', maxes) ``` | Max Serial Number | | --- | | 280 | | 253 | | 294 | | 299 | | 298 | | 237 | | 296 | | 297 | | 293 | | 295 | （省略了 740 行） ```py every_ten = np.arange(1, N+100, 10) Table().with_column('Max Serial Number', maxes).hist(bins = every_ten) ```  這是 750 個估計值的直方圖，每個估計值是統計量“觀察到的最大序列號”的觀測值。 正如你所看到的，盡管在理論上它們可能會小得多，但估計都在 300 附近。直方圖表明，作為飛機總數的估計，最大的序列號可能低了大約 10 到 25 個。但是，飛機的真實數量低了 50 個是不太可能的。 ### 良好的近似 我們前面提到過，如果生成所有可能的樣本，并計算每個樣本的統計量，那么你將準確了解統計量可能有多么不同。事實上，你將會完整地列舉統計量的所有可能值及其所有概率。 換句話說，你將得到統計量的概率分布和概率直方圖。 統計量的概率分布也稱為統計量的抽樣分布，因為它基于所有可能的樣本。 但是，我們上面已經提到，可能的樣本總數往往非常大。例如，如果有 300 架飛機，你可以看到的，30 個序列號的可能序列總數為： ```py 300**30 205891132094649000000000000000000000000000000000000000000000000000000000000 ``` 這是很多樣本。 幸運的是，我們不必生成所有這些。 我們知道統計量的經驗直方圖，基于許多但不是全部可能的樣本，是概率直方圖的很好的近似。 因此統計量的經驗分布讓我們很好地了解到，統計量可能有多么不同。 確實，統計量的概率分布包含比經驗分布更準確的統計量信息。 但是，正如在這個例子中一樣，通常經驗分布所提供的近似值，足以讓數據科學家了解統計量可以變化多少。 如果你有一臺計算機，經驗分布更容易計算。 因此，當數據科學家試圖理解統計的性質時，通常使用經驗分布而不是精確的概率分布。 ### 參數的不同估計 這里舉一個例子來說明這一點。 到目前為止，我們已經使用了最大的觀測序號作為飛機總數的估計。 但還有其他可能的估計，我們現在將考慮其中之一。 這個估計的基本思想是觀察到的序列號的平均值可能在1到`N`之間。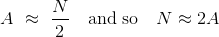 因此，如果`A`是平均值，那么：  因此，可以使用一個新的統計量化來估計飛機總數：取觀測到的平均序列號并加倍。 與使用最大的觀測數據相比，這種估計方法如何？ 計算新統計量的概率分布并不容易。 但是和以前一樣，我們可以模擬它來近似得到概率。 我們來看看基于重復抽樣的統計量的經驗分布。 為了便于比較，重復次數選擇為 750，與之前的模擬相同。 ```py maxes = make_array() twice_ave = make_array() for i in np.arange(repetitions): sampled_numbers = serialno.sample(sample_size) new_max = sampled_numbers.column(0).max() maxes = np.append(maxes, new_max) new_twice_ave = 2*np.mean(sampled_numbers.column(0)) twice_ave = np.append(twice_ave, new_twice_ave) results = Table().with_columns( 'Repetition', np.arange(1, repetitions+1), 'Max', maxes, '2*Average', twice_ave ) results ``` | Repetition | Max | 2*Average | | --- | --- | --- | | 1 | 296 | 312.067 | | 2 | 283 | 290.133 | | 3 | 290 | 250.667 | | 4 | 296 | 306.8 | | 5 | 298 | 335.533 | | 6 | 281 | 240 | | 7 | 300 | 317.267 | | 8 | 295 | 322.067 | | 9 | 296 | 317.6 | | 10 | 299 | 308.733 | （省略了 740 行） 請注意，與所觀察到的最大數字不同，新的估計值（“平均值的兩倍”）可能會高估飛機的數量。 當觀察到的序列號的平均值接近于`N`而不是`1`時，就會發生這種情況。 下面的直方圖顯示了兩個估計的經驗分布。 ```py results.drop(0).hist(bins = every_ten) ```  你可以看到，原有方法幾乎總是低估; 形式上，我們說它是有偏差的。 但它的變異性很小，很可能接近真正的飛機總數。 新方法高估了它，和低估的頻率一樣，因此從長遠來看，平均而言大致沒有偏差。 然而，它比舊的估計更可變，因此容易出現較大的絕對誤差。 這是一個偏差 - 變異性權衡的例子，在競爭性估計中并不罕見。 你決定使用哪種估計取決于對你最重要的誤差種類。 就敵機而言，低估總數可能會造成嚴重的后果，在這種情況下，你可能會選擇使用更加可變的方法，它一半幾率都是高估的。 另一方面，如果高估導致了防范不存在的飛機的不必要的高成本，那么你可能會對低估的方法感到滿意。 ### 技術注解 事實上，“兩倍均值”不是無偏的。平均而言，它正好高估了 1。例如，如果`N`等于 3，來自`1,2,3`的抽取結果的均值是`2`，`2 x 2 = 4`，它比`N`多了 1。“兩倍均值”減 1 是`N`的無偏估計量。