二、簡單數字的奇特技巧 · 面向機器學習的特征工程

# 二、簡單數字的奇特技巧 > 譯者：[@coboe](https://github.com/coboe) > > 校對者：[@ZiseonJiao](https://github.com/emengjzs) 在深入研究諸如文本和圖像這樣的復雜數據類型之前，讓我們先從最簡單的數字數據開始。它們可能來自各種來源：地理位置或人、購買的價格、傳感器的測量、交通計數等。數字數據已經是數學模型容易消化的格式。這并不意味著不再需要特征工程。好的特征不僅代表數據的顯著方面，而且符合模型的假設。因此，轉換常常是必要的。數字特征工程技術是基礎。當原始數據被轉換為數字特征時，它們可以被應用。數值數據的第一個健全檢查是大小是否重要。我們只需要知道它是正面的還是負面的？或者我們只需要知道一個非常粗粒度的大小？這一明智的檢查對于自動累積數尤其重要，比如統計，每天訪問網站的次數，餐館所獲得的評論數量等等。接下來，考慮特征的規模。最大值和最小值是什么？它們跨越幾個數量級嗎？輸入特性平滑的模型對輸入的尺度敏感。例如，3x+ 1是輸入X的簡單線性函數，其輸出的規模直接取決于輸入的比例。其他例子包括k-均值聚類，最近鄰居方法，RBF內核，以及使用歐幾里得距離的任何東西。對于這些模型和建模組件，通常規范化特征以使輸出保持在預期的規模上通常是一個好主意。另一方面，邏輯函數對輸入特征量表不敏感。無論輸入是什么，它們的輸出都是二進制的。例如，邏輯，并采取任何兩個變量和輸出1，當且僅當兩個輸入均為真。邏輯函數的另一個例子是階躍函數“輸入x大于5”。決策樹模型由輸入特征的階躍函數組成。因此，基于空間劃分樹（決策樹、梯度提升機、隨機森林）的模型對尺度不敏感。唯一的例外是如果輸入的規模隨著時間的增長而增長，那么如果該特征是某種類型的累積計數。最終它將生長在樹被訓練的范圍之外。如果可能是這樣的話，那么就有必要周期性地重新調整輸入。另一個解決方案是第5章討論的bin計數方法。考慮數值特征的分布也是很重要的。分布總結了承擔特定價值的可能性。輸入特征的分布對某些模型比其他模型更重要。例如，線性回歸模型的訓練過程假定預測誤差分布得像高斯。這通常是好的，除非預測目標在幾個數量級上擴散。在這種情況下，高斯誤差假設可能不再成立。解決這一問題的一種方法是轉變產出目標，以馴服規模的增長。（嚴格地說，這將是目標工程，而不是特征工程。）對數變換，這是一種功率變換，將變量的分布接近高斯。另一個解決方案是第5章討論的bin計數方法。除了裁剪模型或培訓過程的假設, 多個功能可以組合成更復雜的功能。希望復雜的功能能夠更簡潔地捕捉原始數據中的重要信息。通過使輸入功能更加 "雄辯", 模型本身可以更簡單, 更容易進行培訓和評估, 并做出更好的預測。作為一個極端的, 復雜的特點本身可能是統計模型的輸出。這是一個稱為模型堆疊的概念, 我們將在7章和8章中更詳細地討論。在本章中, 我們給出了復雜特征的最簡單示例: 交互功能。交互特征易于制定，但特征的組合導致更多的輸入到模型中。為了減少計算開銷，通常需要使用自動特征選擇來修剪輸入特征。我們將從標量、向量和空間的基本概念開始，然后討論尺度、分布、交互特征和特征選擇。 ## 標量、向量和空間在我們開始之前, 我們需要定義一些基本概念, 這本書的其余部分。單個數字特征也稱為標量。標量的有序列表稱為向量。向量位于向量空間中。在絕大多數機器學習應用中, 對模型的輸入通常表示為數字向量。本書的其余部分將討論將原始數據轉換為數字向量的最佳實踐策略. 向量可以被可視化為空間中的一個點。（有時人們從原點到那一點畫一條線和一個箭頭。在這本書中，我們將主要使用這一點。例如，假設我們有一個二維向量v=[1，-1]。也就是說，向量包含兩個數，在第一方向d1中，向量具有1的值，并且在第二方向d2中，它具有-1的值。我們可以在二維圖中繪制v。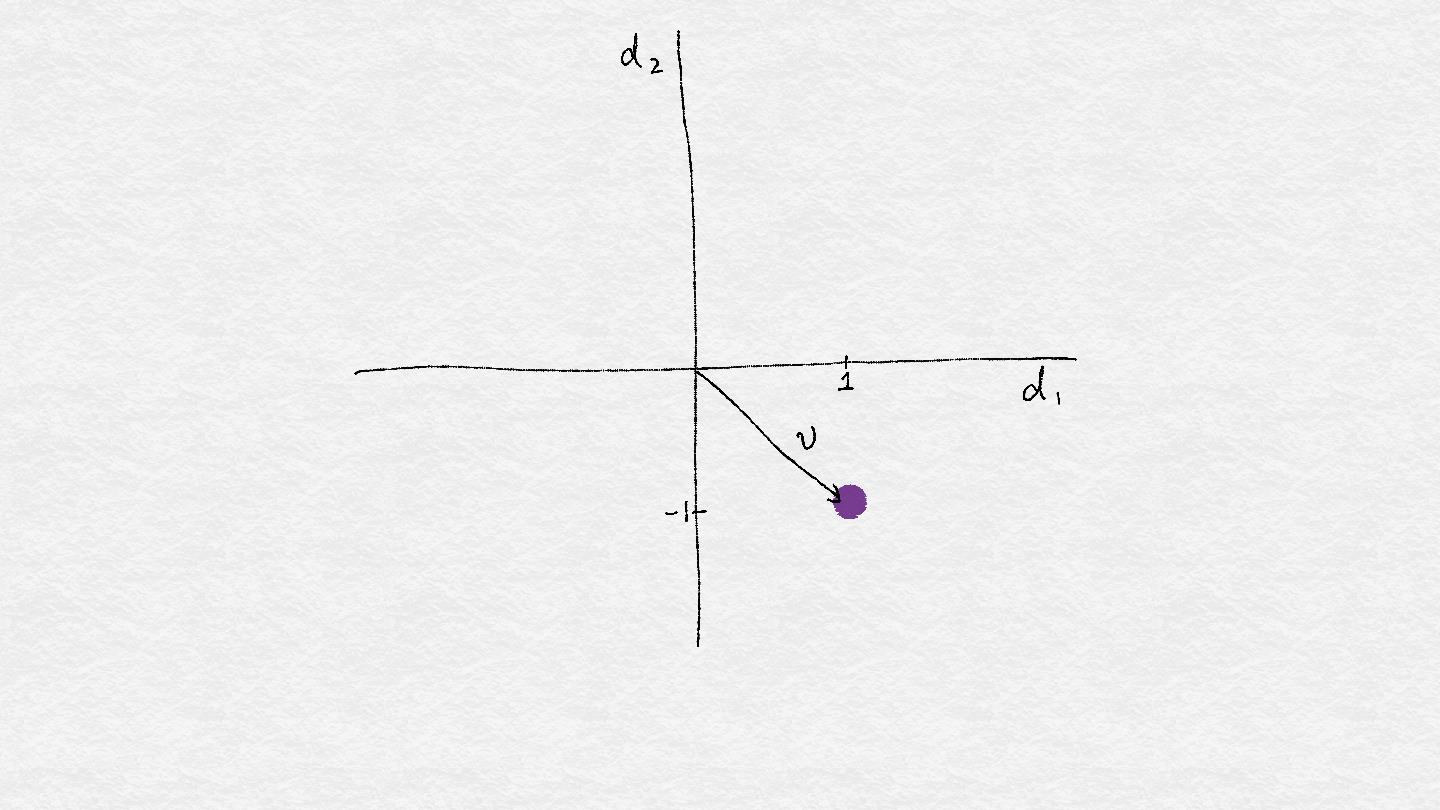 ![A single vector](https://img.kancloud.cn/9d/ba/9dba6d29ac24b4768508a206b806c5b7_1440x810.png) **Figure 2-1. A single vector.** 在數據世界中, 抽象向量及其特征維度具有實際意義。例如, 它可以代表一個人對歌曲的偏愛。每首歌都是一個特征, 其中1的值相當于大拇指向上,-1 個拇指向下。假設向量 v 表示一個聽眾 Bob 的喜好。Bob喜歡 Bob Dylan 的 “Blowin’ in the Wind” 和 Lady Gaga 的 "Poker Face"。其他人可能有不同的喜好。總的來說, 數據集合可以在特征空間中可視化為點云. 相反，一首歌可以由一組人的個人喜好來表示。假設只有兩個聽眾，Alice 和 Bob。Alice 喜歡 Leonard Cohen 的 “Poker Face”, “Blowin’ in the Wind” 和 “Hallelujah”，但討厭 Katy Perry 的 “Roar” 和 Radiohead 的 “Creep”。Bob 喜歡 “Roar", “Hallelujah”和“Blowin’ in the Wind”，但討厭 “Poker Face” 和 “Creep” 。在聽眾的空間里，每一首歌都是一個點。就像我們可以在特征空間中可視化數據一樣，我們可以在數據空間中可視化特征。圖2-2顯示了這個例子。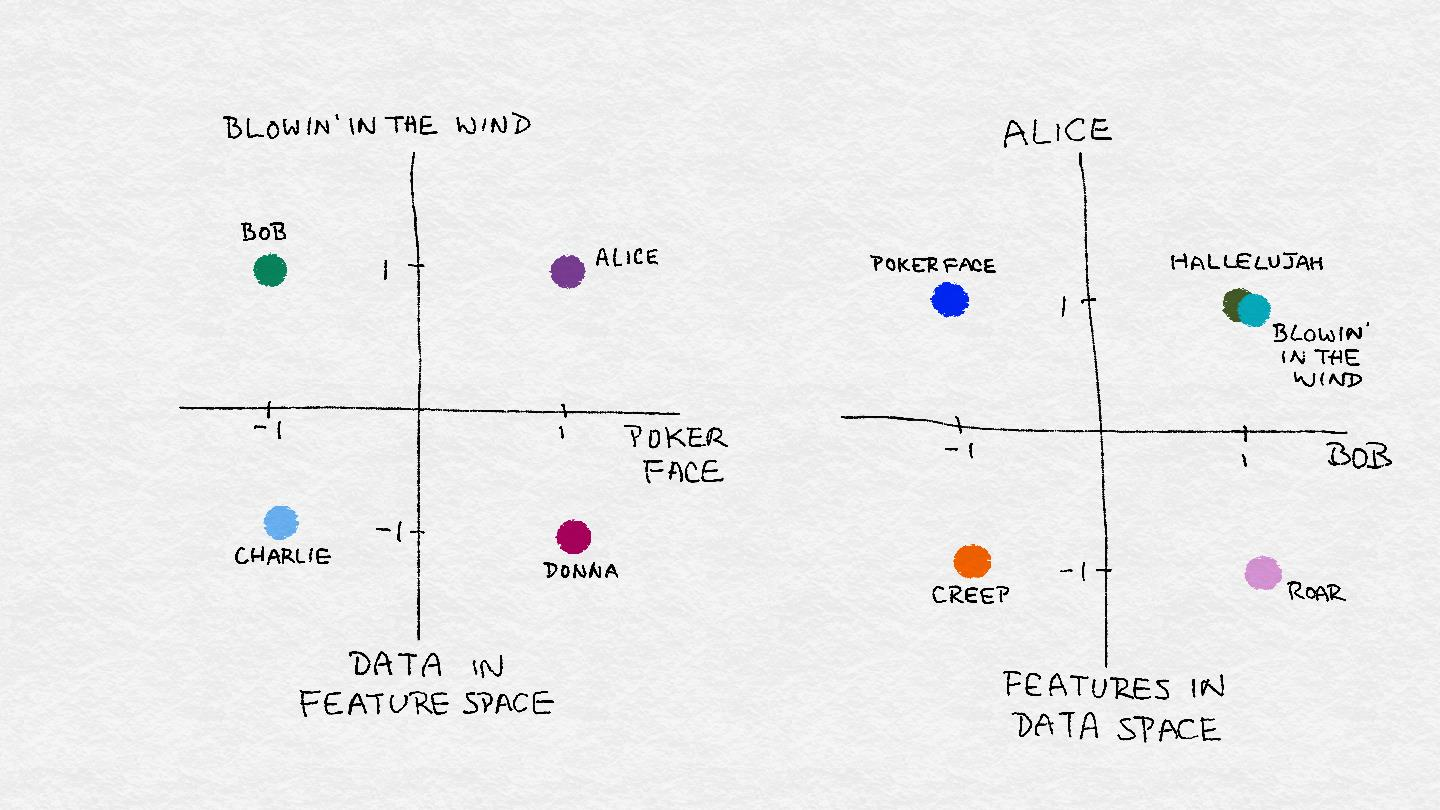 ![Illustration of feature space vs. data space](https://img.kancloud.cn/a4/06/a4069bc74c642b317352358d21e69268_1440x810.png) **Figure 2-2. Illustration of feature space vs. data space.** ## 處理計數在大數據時代，計數可以快速積累而不受約束。用戶可以將歌曲或電影放在無限播放中，或者使用腳本反復檢查流行節目的門票可用性，這會導致播放次數或網站訪問計數迅速上升。當數據可以以高的體積和速度產生時，它們很可能包含一些極值。這是一個好主意，檢查他們的規模，并確定是否保持它們作為原始數字，將它們轉換成二進制變量，以指示存在，或將它們放入粗粒度。 ## 二值化 Million Song 數據集中的用戶品味畫像包含了一百萬個用戶在 Echo Nest 的完整音樂聆聽歷史。下面是有關數據集的一些相關統計數據。 ### Echo Nest 品味畫像數據集的統計 - 有超過4800萬個用戶ID、音樂ID和監聽計數三元組。 - 完整的數據集包含1019318個獨特用戶和384546首獨特歌曲。 - 引文：Echo Nest 品味畫像的數據子集，官方的 Million Song 數據集的用戶數據集，可從這里獲得：http://labrosa.ee.columbia.edu/millionsong/tasteprofile 假設任務是建立一個推薦器向用戶推薦歌曲。推薦器的一個組件可以預測用戶將對一首特別的歌曲會有多少喜歡。由于數據包含實際的聽歌次數，這應該是預測的目標嗎？如果一個大的聽計數意味著用戶真的喜歡這首歌，反之亦然，那是正確的。然而，數據表明，雖然99%的聽計數是24或更低，也有一些聽計數數以千計，最大為9667。（如圖2-3所示，直方圖最接近于0的bin中的峰值。但是超過10000個三元組的計數更大，幾千個則有幾個。這些值異常大；如果我們試圖預測實際的聽計數，那么模型將被這些大的值拉離。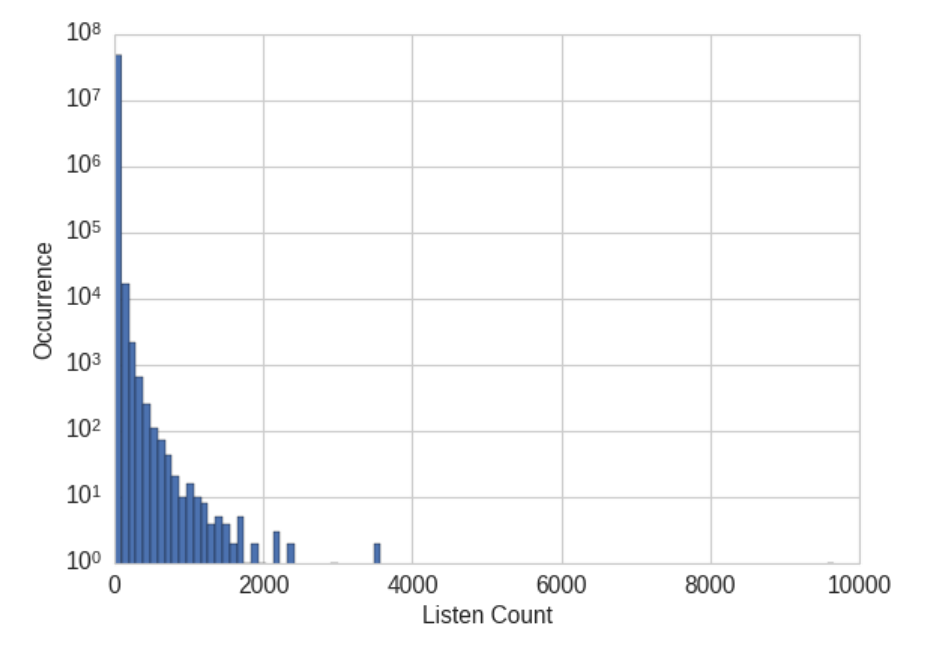 ![Histogram of listen counts in the user taste profile of the Million Song Dataset. Note that the y-axis is on a log scale.](https://img.kancloud.cn/c1/9c/c19cc34c47abe4056fa3631ea1596d5b_926x646.png) **Figure 2-3. Histogram of listen counts in the user taste profile of the Million Song Dataset. Note that the y-axis is on a log scale.** 在 Million Song 數據集中，原始監聽計數不是用戶口味的可靠度量。（在統計術語中，健壯性意味著該方法在各種各樣的條件下工作。）用戶有不同的聽力習慣。有些人可能把他們最喜歡的歌曲放在無限的循環中，而其他人可能只在特殊的場合品嘗它們。很難說聽一首歌20次的人一定喜歡聽10次的人的兩倍。用戶偏好的更健壯表示是使計數二元化和修剪所有大于1的計數為1。換句話說，如果用戶至少聽過一首歌，那么我們將其視為用戶喜歡歌曲。這樣，模型不需要花費周期來預測原始計數之間的微小差異。二進制目標是用戶偏好的簡單而穩健的度量。 ### 例子2-1。使 Million Song 數據集中聽歌計數二進制化。 ``` import pandas as pd listen_count = pd.read_csv('millionsong/train_triplets.txt.zip', header=None, delimiter='\t') # The table contains user-song-count triplets. Only non-zero counts are # included. Hence to binarize the count, we just need to set the entire # count column to 1. listen_count[2] = 1 ``` 這是我們設計模型目標變量的一個例子。嚴格地說, 目標不是一個特征, 因為它不是輸入。但有時我們確實需要修改目標以解決正確的問題。 ## 量化或裝箱對于本練習, 我們從第 6 輪 Yelp 數據集挑戰中采集數據, 并創建一個更小的分類數據集。Yelp 數據集包含用戶對來自北美和歐洲十個城市的企業的評論。每個商戶都標記為零個或多個類別。以下是有關數據集的相關統計信息。 ### 關于第 6 輪 Yelp 數據集的統計 - 有782種商戶類別。 - 完整的數據集包含 1569264 個（約1.6M）評論和 61184 個（61K）商戶。 - “餐廳”（990627個評論）和“夜生活”（210028個評論）是最流行的類別，評論計數是明智的。 - 沒有一個商戶同時屬于餐廳和夜生活分類。因此，這兩組評論之間沒有重疊。每個商戶都有一個評論計數。假設我們的任務是使用協同過濾來預測用戶可能給企業的評級。評論計數可能是一個有用的輸入特征，因為通常在流行和良好的評級之間有很強的相關性。現在的問題是，我們應該使用原始評論計數或進一步處理它嗎？圖2-4顯示了所有商戶評論計數的直方圖。我們看到和音樂聽歌計數一樣的模式。大部分的統計數字都很小，但一些企業有成千上萬的評論。 ### 例子2-2。在YELP數據集中可視化商戶評論計數。 ``` >>> import pandas as pd >>> import json ### Load the data about businesses >>> biz_file = open('yelp_academic_dataset_business.json') >>> biz_df = pd.DataFrame([json.loads(x) for x in biz_file.readlines()]) >>> biz_file.close() >>> import matplotlib.pyplot as plt >>> import seaborn as sns ### Plot the histogram of the review counts >>> sns.set_style('whitegrid') >>> fig, ax = plt.subplots() >>> biz_df['review_count'].hist(ax=ax, bins=100) >>> ax.set_yscale('log') >>> ax.tick_params(labelsize=14) >>> ax.set_xlabel('Review Count', fontsize=14) >>> ax.set_ylabel('Occurrence', fontsize=14) ``` ![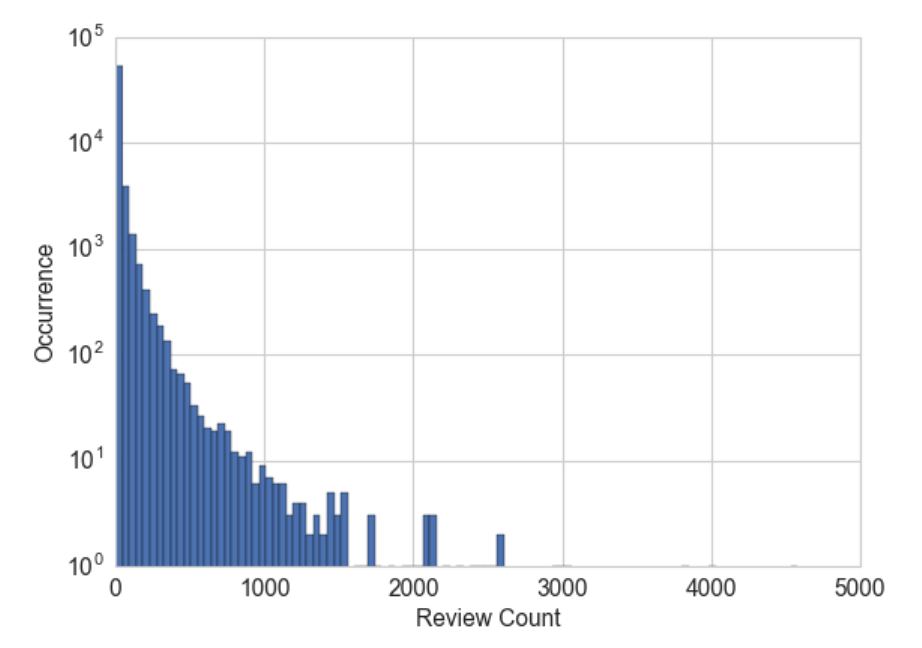review count](https://img.kancloud.cn/28/90/28909896018325aa5a8875813321cfc9_922x648.png) **Figure 2-4. Histogram of business review counts in the Yelp reviews dataset. The y-axis is on a log-scale.** 對于許多模型來說，跨越數個數量級的原始計數是有問題的。在線性模型中，相同的線性系數必須對計數的所有可能值工作。大量的計數也可能破壞無監督學習方法，如k-均值聚類，它使用相似性函數來測量數據點之間的相似性。k-均值使用數據點之間的歐幾里得距離。數據向量的一個元素中的大計數將超過所有其他元素中的相似性，這可能會丟棄整個相似性度量。一種解決方案是通過量化計數來包含標量。換句話說，我們將計數分組到容器中，并且去掉實際的計數值。量化將連續數映射成離散數。我們可以把離散化的數字看作是代表強度度量的容器的有序的序列。為了量化數據，我們必須決定每一個箱子應該有多寬。解決方案分為固定寬度或自適應兩種類型。我們將給出每個類型的例子。 ### 固定寬度裝箱對于固定寬度裝箱, 每個 bin 都包含一個特定的數值范圍。范圍可以是定制設計或自動分割, 它們可以線性縮放或指數縮放。例如, 我們可以將一個人的年齡分組為十年: 0-9 歲歸納到bin 1, 10-19 年歸納到 bin 2 等。要從計數映射到 bin, 只需除以 bin 的寬度并取整部分。也經常看到定制設計的年齡范圍更適合于生活的階段： - 0-12 歲 - 12-17 歲 - 18-24 歲 - 25-34 歲 - 35-44 歲 - 45-54 歲 - 55-64 歲 - 65-74 歲 - 75 歲以上當數字跨越多個數量級時，最好用10個冪（或任何常數的冪）來分組：0－9、10-99、100-999、100-9999等。容器寬度呈指數增長，從O（10）、O（100）到O（1000）和以上。要從計數映射到bin，取計數的log值。指數寬度的劃分與對數變換非常相關，我們在“對數變換”中討論。 ### 例子2-3。用固定寬度的箱進行量化計數 ``` >>> import numpy as np ### Generate 20 random integers uniformly between 0 and 99 >>> small_counts = np.random.randint(0, 100, 20) >>> small_counts array([30, 64, 49, 26, 69, 23, 56, 7, 69, 67, 87, 14, 67, 33, 88, 77, 75, 47, 44, 93]) ### Map to evenly spaced bins 0-9 by division >>> np.floor_divide(small_counts, 10) array([3, 6, 4, 2, 6, 2, 5, 0, 6, 6, 8, 1, 6, 3, 8, 7, 7, 4, 4, 9], dtype=int32) ### An array of counts that span several magnitudes >>> large_counts = [296, 8286, 64011, 80, 3, 725, 867, 2215, 7689, 11495, 91897, 44, 28, 7971, 926, 122, 22222] ### Map to exponential-width bins via the log function >>> np.floor(np.log10(large_counts)) array([ 2., 3., 4., 1., 0., 2., 2., 3., 3., 4., 4., 1., 1., 3., 2., 2., 4.]) ``` ### 分位數裝箱固定寬度裝箱很容易計算。但是如果計數有很大的差距, 那么將會有許多空的垃圾箱沒有數據。該問題可以通過基于數據分布的垃圾箱自適應定位來解決。這可以使用分發的分位數來完成。分位數是將數據劃分為相等部分的值。例如, 中位數將數據分成一半;一半的數據是較小的, 一半大于中位數。分位數把數據分成幾個部分, 十分位數把數據劃分成十份。示例2-4 演示如何計算 Yelp 商戶評論數的十等分, 圖2-5 覆蓋直方圖上的十等分。這就更清楚地說明了對更小的計數的歪斜。 ### 例子 2-4。計算 Yelp 商戶評論數的十分位數 ``` >>> deciles = biz_df['review_count'].quantile([.1, .2, .3, .4, .5, .6, .7, .8, .9]) >>> deciles 0.1 3.0 0.2 4.0 0.3 5.0 0.4 6.0 0.5 8.0 0.6 12.0 0.7 17.0 0.8 28.0 0.9 58.0 Name: review_count, dtype: float64 ### Visualize the deciles on the histogram >>> sns.set_style('whitegrid') >>> fig, ax = plt.subplots() >>> biz_df['review_count'].hist(ax=ax, bins=100) >>> for pos in deciles: ... 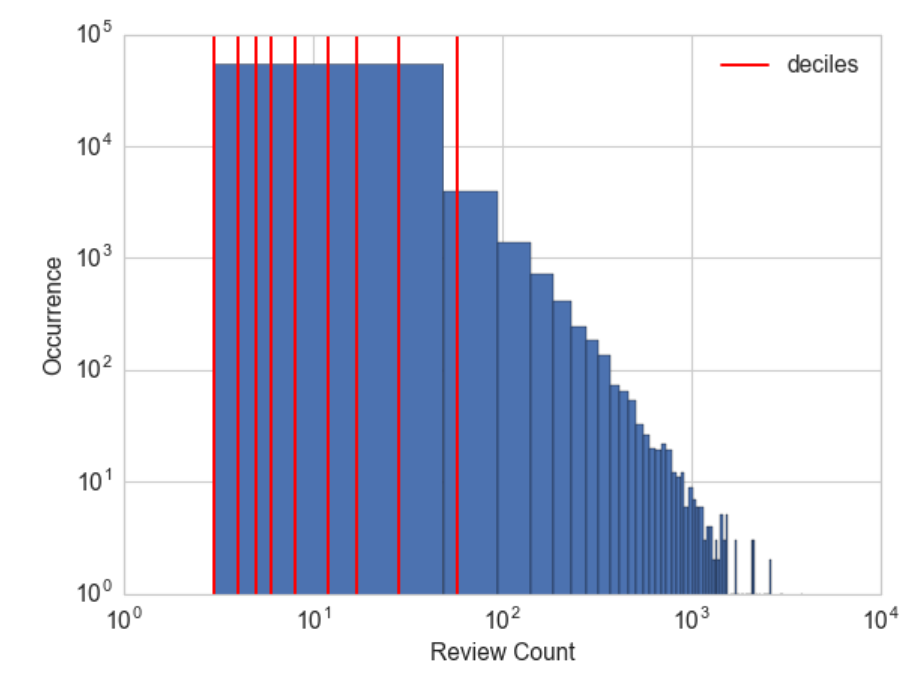handle = plt.axvline(pos, color='r') >>> ax.legend([handle], ['deciles'], fontsize=14) >>> ax.set_yscale('log') >>> ax.set_xscale('log') >>> ax.tick_params(labelsize=14) >>> ax.set_xlabel('Review Count', fontsize=14) >>> ax.set_ylabel('Occurrence', fontsize=14) ``` ![Deciles of the review counts in the Yelp reviews dataset](https://img.kancloud.cn/3c/72/3c72b006ecbf12924d5740f2b2c955d9_924x676.png) **Figure 2-5. Deciles of the review counts in the Yelp reviews dataset. Note that both x- and y-axes are in log scale.** 為了計算分位數和映射數據到分位數箱，我們可以使用 Pandas 庫。 pandas.DataFrame.quantile 和 pandas.Series.quantile 用于計算分位數。pandas.qcut將數據映射到所需數量的分位數。 ### 例子2-5。按分位數分箱計數。 ``` ### Continue example Example 2-3 with large_counts >>> import pandas as pd ### Map the counts to quartiles >>> pd.qcut(large_counts, 4, labels=False) array([1, 2, 3, 0, 0, 1, 1, 2, 2, 3, 3, 0, 0, 2, 1, 0, 3], dtype=int64) ### Compute the quantiles themselves >>> large_counts_series = pd.Series(large_counts) >>> large_counts_series.quantile([0.25, 0.5, 0.75]) 0.25 122.0 0.50 926.0 0.75 8286.0 dtype: float64 ``` ## 對數轉換在“量化或裝箱”中，我們簡要地介紹了把計數的對數映射到指數寬度箱的概念。讓我們現在再看一看。對數函數是指數函數的逆。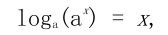它定義為 ![log function](https://img.kancloud.cn/2c/09/2c09c2921b6896a8394dce4dee9f3b6c_168x35.png) 其中 a 為正常數, x 可以是任何正數。由于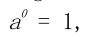![a exponential function](https://img.kancloud.cn/f4/f4/f4f4738be9c4ae898acb8ea263eb43f3_87x37.png)我們有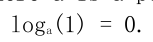![a log function](https://img.kancloud.cn/c6/e3/c6e3e7ea15645857e8102e5f9e234834_153x42.png)這意味著對數函數將小范圍的數字 (0、1) 映射到負數的整個范圍 (-∞, 0)。函數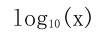![log function](https://img.kancloud.cn/e9/5c/e95cf2ffec10e35e123f9eba35627b1b_103x37.png) 將 [1、10] 映射到 [0、1]、將[10、100] 映射到 [1、2] 等等。換言之, 對數函數壓縮大數的范圍, 并擴展小數的范圍。越大的 x , log(x)的增量越慢。通過查看 log 函數的圖像, 可以更容易地消化這一點。(見圖2-6)。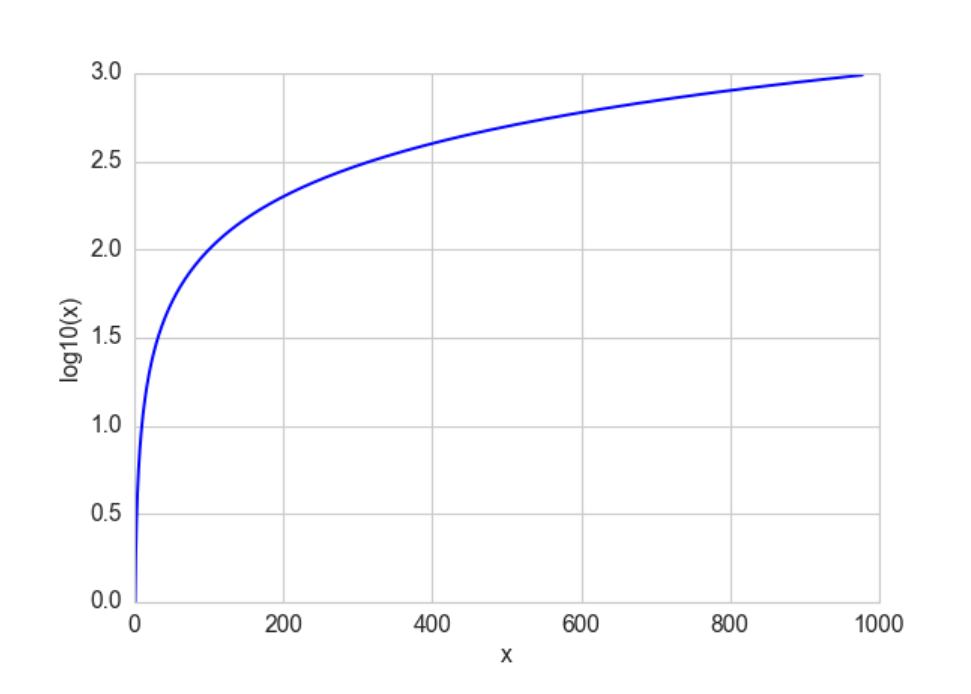 ![The log function](https://img.kancloud.cn/29/8c/298c7e50eba8f053599ff4b4b6fade77_971x694.png) **Figure 2-6. The log function compresses the high numeric range and expands the low range. Note how the horizontal x values from 100 to 1000 got compressed into just 2.0 to 3.0 in the vertical y range, while the tiny horizontal portion of x values less than 100 are mapped to the rest of the vertical range.** 對數變換是處理具有重尾分布的正數的有力工具。（重尾分布在尾部范圍內的概率比高斯分布的概率大）。它將分布在高端的長尾壓縮成較短的尾部，并將低端擴展成較長的頭部。圖2-7比較d對數轉換之前和之后的YELP商戶評論計數的直方圖。Y軸現在都在正常（線性）尺度上。在（0.5，1）范圍內的底部圖中增加的倉間隔是由于在1和10之間只有10個可能的整數計數。請注意，原始審查計數非常集中在低計數區域，離群值在4000以上。對數變換后，直方圖不集中在低端，更分散在X軸上。 ### 例子2-6。可視化對數變換前后評論數分布 ``` fig, (ax1, ax2) = plt.subplots(2,1) biz_df['review_count'].hist(ax=ax1, bins=100) ax1.tick_params(labelsize=14) ax1.set_xlabel('review_count', fontsize=14) ax1.set_ylabel('Occurrence', fontsize=14) biz_df['log_review_count'].hist(ax=ax2, bins=100) ax2.tick_params(labelsize=14) ax2.set_xlabel('log10(review_count))', fontsize=14) ax2.set_ylabel('Occurrence', fontsize=14) ``` ![](https://img.kancloud.cn/69/fd/69fd5cd98fdc37147f20b0dde1c6a019_942x962.png) **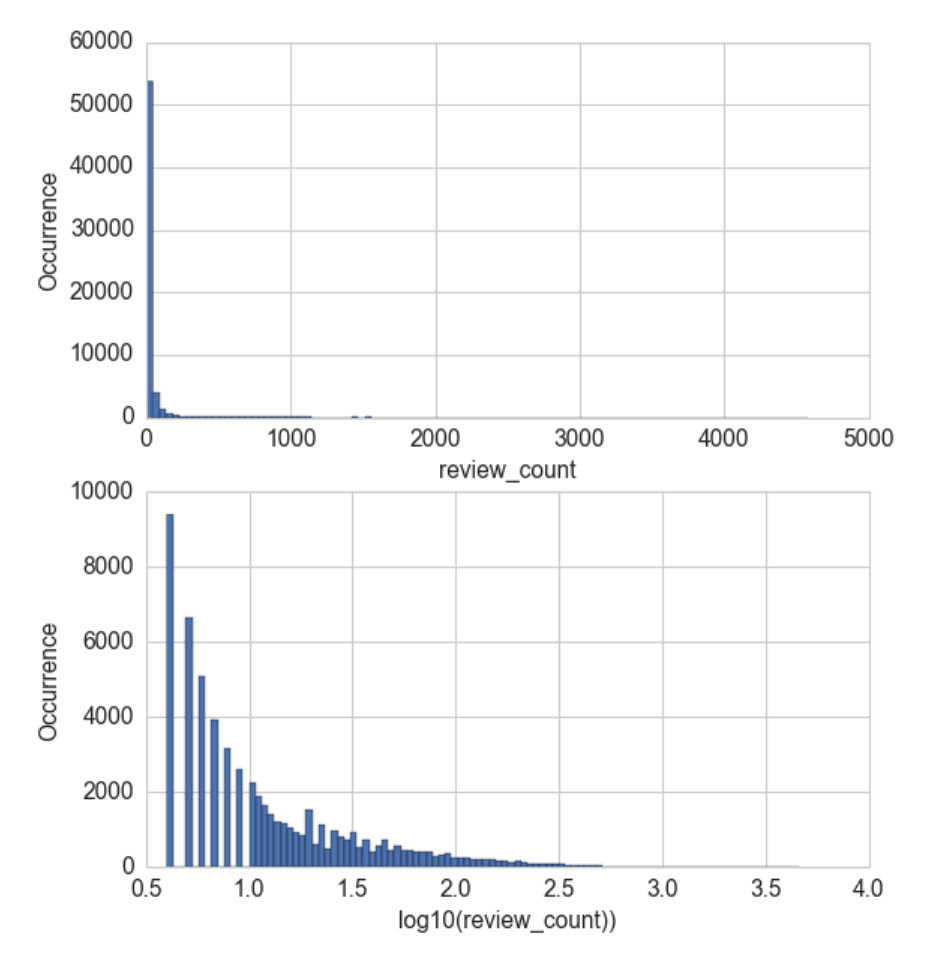Figure 2-7. Comparison of Yelp business review counts before (top) and after (bottom) log transformation.** 另一個例子是來自 UC Irvine 機器學習庫的在線新聞流行數據集。以下是有關數據集的相關統計信息。 ### 在線新聞流行數據集的統計 - 該數據集包括 MasHabor 在兩年的時間內出版的 39797 個新聞文章的60個特征。 - 引證: K. Fernandes, P. Vinagre 和 P. Cortez . 一種用于預測在線新聞的流行程度的主動智能決策支持系統。2015 第十七屆 EPIA 活動, 葡萄牙人工智能會議論文集, 9月, 葡萄牙科英布拉。目的是利用這些特征來預測文章在社交媒體上的用分享數量表示的流行度。在本例中, 我們將只關注一個特征——文章中的單詞數。圖2-8 顯示了對數轉換前后特征的直方圖。請注意, 在對數轉換后, 分布看起來更高斯, 除了長度為零的文章 (無內容) 的斷裂。 ### 例子2-7。可視化在有對數變換和沒有對數變換時新聞文章流行度的分布。 ``` fig, (ax1, ax2) = plt.subplots(2,1) df['n_tokens_content'].hist(ax=ax1, bins=100) ax1.tick_params(labelsize=14) ax1.set_xlabel('Number of Words in Article', fontsize=14) ax1.set_ylabel('Number of Articles', fontsize=14) df['log_n_tokens_content'].hist(ax=ax2, bins=100) ax2.tick_params(labelsize=14) ax2.set_xlabel('Log of Number of Words', fontsize=14) ax2.set_ylabel('Number of Articles', fontsize=14) ``` ![](https://img.kancloud.cn/d5/9c/d59cf196172cc0c63be7e28238b3fad3_993x840.png) **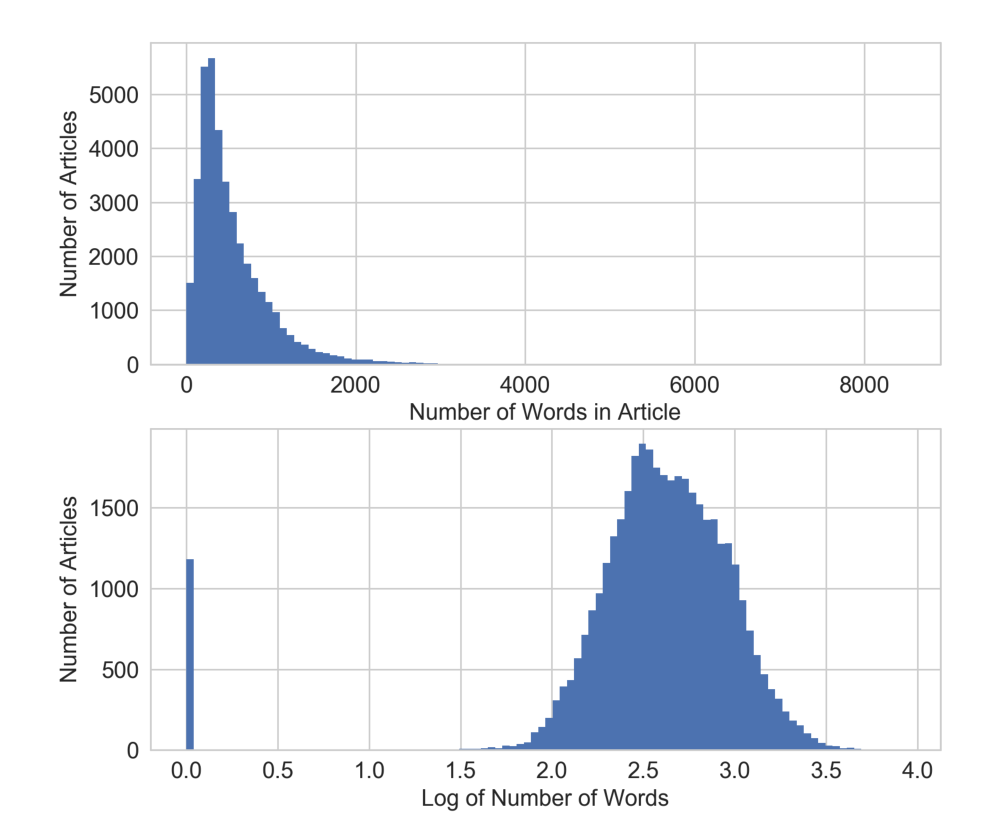Figure 2-8. Comparison of word counts in Mashable news articles before (top) and after (bottom) log transformation.** ## 對數轉換實戰讓我們看看在監督學習中對數轉換如何執行。我們將使用上面的兩個數據集。對于 Yelp 評論數據集, 我們將使用評論的數量來預測商戶的平均評級。對于 Mashable 的新聞文章, 我們將使用文章中的字數來預測其流行程度。由于輸出是連續的數字, 我們將使用簡單的線性回歸作為模型。我們在沒有對數變換和有對數變換的特色上，使用 Scikit Learn 執行10折交叉驗證的線性回歸。模型由 R 方評分來評估, 它測量訓練后的回歸模型預測新數據的良好程度。好的模型有較高的 R 方分數。一個完美的模型得到最高分1。分數可以是負的, 一個壞的模型可以得到一個任意低的負評分。通過交叉驗證, 我們不僅得到了分數的估計, 還獲得了方差, 這有助于我們判斷兩種模型之間的差異是否有意義。 ### 例子2-8。使用對數轉換 YELP 評論數預測平均商戶評級 ``` >>> import pandas as pd >>> import numpy as np >>> import json >>> from sklearn import linear_model >>> from sklearn.model_selection import cross_val_score ## Using the previously loaded Yelp reviews dataframe, ## compute the log transform of the Yelp review count. ## Note that we add 1 to the raw count to prevent the logarithm from ## exploding into negative infinity in case the count is zero. >>> biz_df['log_review_count'] = np.log10(biz_df['review_count'] + 1) ## Train linear regression models to predict the average stars rating of a business, ## using the review_count feature with and without log transformation ## Compare the 10-fold cross validation score of the two models >>> m_orig = linear_model.LinearRegression() >>> scores_orig = cross_val_score(m_orig, biz_df[['review_count']], biz_df['stars'], cv=10) >>> m_log = linear_model.LinearRegression() >>> scores_log = cross_val_score(m_log, biz_df[['log_review_count']], biz_df['stars'], cv=10) >>> print("R-squared score without log transform: %0.5f (+/- %0.5f)" % (scores_orig.mean(), scores_orig.std() * 2)) >>> print("R-squared score with log transform: %0.5f (+/- %0.5f)" % (scores_log.mean(), scores_log.std() * 2)) R-squared score without log transform: -0.03683 (+/- 0.07280) R-squared score with log transform: -0.03694 (+/- 0.07650) ``` 從實驗的結果來看, 兩個簡單的模型 (有對數變換和沒有對數變換) 在預測目標時同樣不好, 而有對數變換的特征表現略差。真令人失望!這并不奇怪, 他們都不是很好, 因為他們都只使用一個功能。但是, 人們本來希望日志轉換的功能執行得更好。讓我們看看對數轉換在線新聞流行數據集上如何表現。 ### 例子2-9。利用經過對數轉換在線新聞數據中的詞數量預測文章流行度 ``` ## Download the Online News Popularirty dataset from UCI, then use ## Pandas to load the file into a dataframe >>> df = pd.read_csv('OnlineNewsPopularity.csv', delimiter=', ') ## Take the log transform of the 'n_tokens_content' feature, which ## represents the number of words (tokens) in a news article. >>> df['log_n_tokens_content'] = np.log10(df['n_tokens_content'] + 1) ## Train two linear regression models to predict the number of shares ## of an article, one using the original feature and the other the ## log transformed version. >>> m_orig = linear_model.LinearRegression() >>> scores_orig = cross_val_score(m_orig, df[['n_tokens_content']], df['shares'], cv=10) >>> m_log = linear_model.LinearRegression() >>> scores_log = cross_val_score(m_log, df[['log_n_tokens_content']], df['shares'], cv=10) >>> print("R-squared score without log transform: %0.5f (+/- %0.5f)" % (scores_orig.mean(), scores_orig.std() * 2)) >>> print("R-squared score with log transform: %0.5f (+/- %0.5f)" % (scores_log.mean(), scores_log.std() * 2)) R-squared score without log transform: -0.00242 (+/- 0.00509) R-squared score with log transform: -0.00114 (+/- 0.00418) ``` 置信區間仍然重疊，但具有對數變換特征的模型比沒有對數變換的表現更好。為什么對數轉換在這個數據集上更成功？我們可以通過觀察輸入特征和目標值的散點圖來得到線索。如圖2-9的底部面板所示，對數變換重塑了X軸，將目標值（大于200000個份額）中的大離群值進一步拉向軸的右手側。這給線性模型在輸入特征空間的低端更多的“呼吸空間”。沒有對數轉換（上部面板），在輸入值變化下非常小的情況下，模型有更大的壓力下適應非常不同的目標值。 ### 示例2-10。可視化新聞流程度預測問題中輸入輸出相關性。 ``` fig2, (ax1, ax2) = plt.subplots(2,1) ax1.scatter(df['n_tokens_content'], df['shares']) ax1.tick_params(labelsize=14) ax1.set_xlabel('Number of Words in Article', fontsize=14) ax1.set_ylabel('Number of Shares', fontsize=14) ax2.scatter(df['log_n_tokens_content'], df['shares']) ax2.tick_params(labelsize=14) ax2.set_xlabel('Log of the Number of Words in Article', fontsize=14) ax2.set_ylabel('Number of Shares', fontsize=14) ``` ![](https://img.kancloud.cn/60/20/60206200018e5a6fe9e00511666b8396_957x831.png) **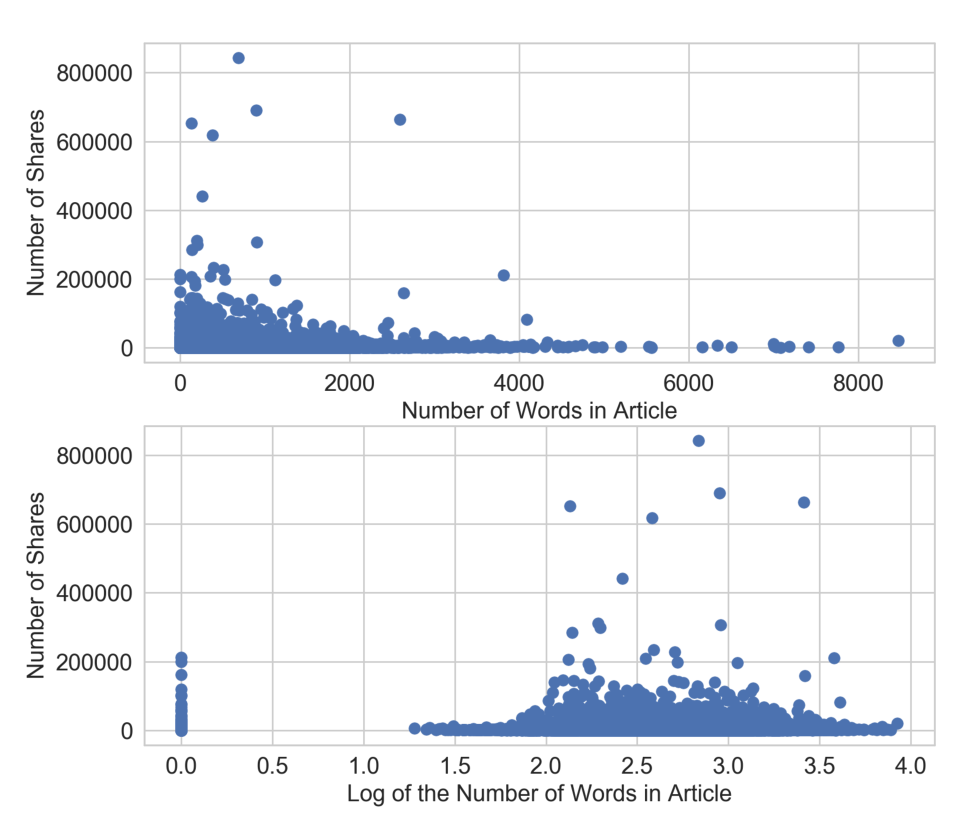Figure 2-9. Scatter plot of number of words (input) vs. number of shares (target) in the Online News dataset. The top plot visualizes the original feature, and the bottom plot shows the scatter plot after log transformation.** 將此與應用于YELP評論數據集的相同散點圖進行比較。圖2-10看起來與圖2-9非常不同。在1到5，步長0.5的區間，平均星級是離散的。高評論計數（大致＞2500評論）與較高的平均星級評級相關。但這種關系遠不是線性的。沒有一種清晰的方法可以根據輸入來預測平均星級。從本質上講，該圖表明，評論數及其對數都是平均星級的不良線性預測因子。 ### 例2-11。可視化 Yelp 商戶評論預測中輸入與輸出的相關性。 ``` fig, (ax1, ax2) = plt.subplots(2,1) ax1.scatter(biz_df['review_count'], biz_df['stars']) ax1.tick_params(labelsize=14) ax1.set_xlabel('Review Count', fontsize=14) ax1.set_ylabel('Average Star Rating', fontsize=14) ax2.scatter(biz_df['log_review_count'], biz_df['stars']) ax2.tick_params(labelsize=14) ax2.set_xlabel('Log of Review Count', fontsize=14) ax2.set_ylabel('Average Star Rating', fontsize=14) ``` ![](https://img.kancloud.cn/77/ac/77ac81176f91ba24e243749c29cda15b_930x813.png) **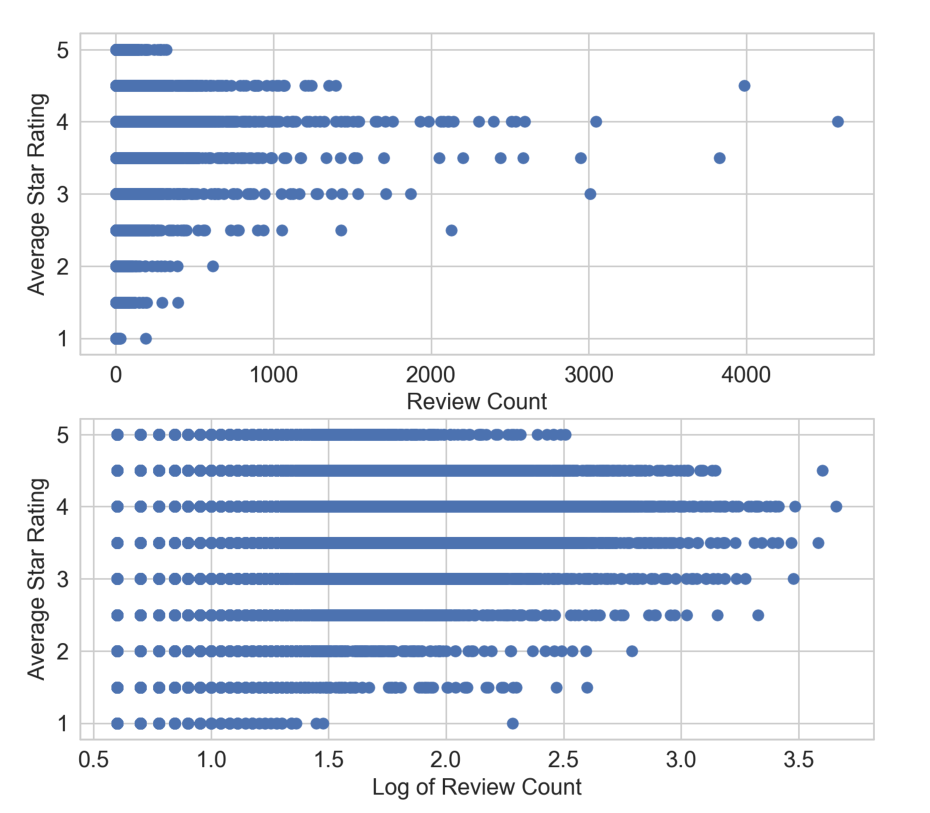Figure 2-10. Scatter plot of review counts (input) vs. average star ratings (target) in the Yelp Reviews dataset. The top panel plots the original review count, and the bottom panel plots the review count after log transformation.** ## 數據可視化的重要性對數變換在兩個不同數據集上的影響的比較，說明了可視化數據的重要性。在這里，我們故意保持輸入和目標變量簡單，以便我們可以很容易地可視化它們之間的關系。如圖2-10所示的曲線，立即顯示所選擇的模型（線性）不可能代表所選擇的輸入和目標之間的關系。另一方面，人們可以令人信服地在給定平均星級模擬評論數的分布。在建立模型時，最好直觀地檢查輸入和輸出之間的關系，以及不同輸入特征之間的關系。 ### 功率變換：對數變換的推廣對數變換是一個稱為功率變換的變換族的特殊例子。在統計方面，這些是方差穩定的變換。為了理解為什么方差穩定是好的，考慮泊松分布。這是一個方差等于它的平均值的重尾分布。因此，它的質量中心越大，其方差越大，尾部越重。功率變換改變變量的分布，使得方差不再依賴于平均值。例如，假設一個隨機變量X具有泊松分布。假如我們使用開平方根變換X, 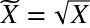![](https://img.kancloud.cn/88/a4/88a4347d36a9fbd32cb40521a2b3714c_90x28.png)的方差大致是恒定的, 而不是等于平均值。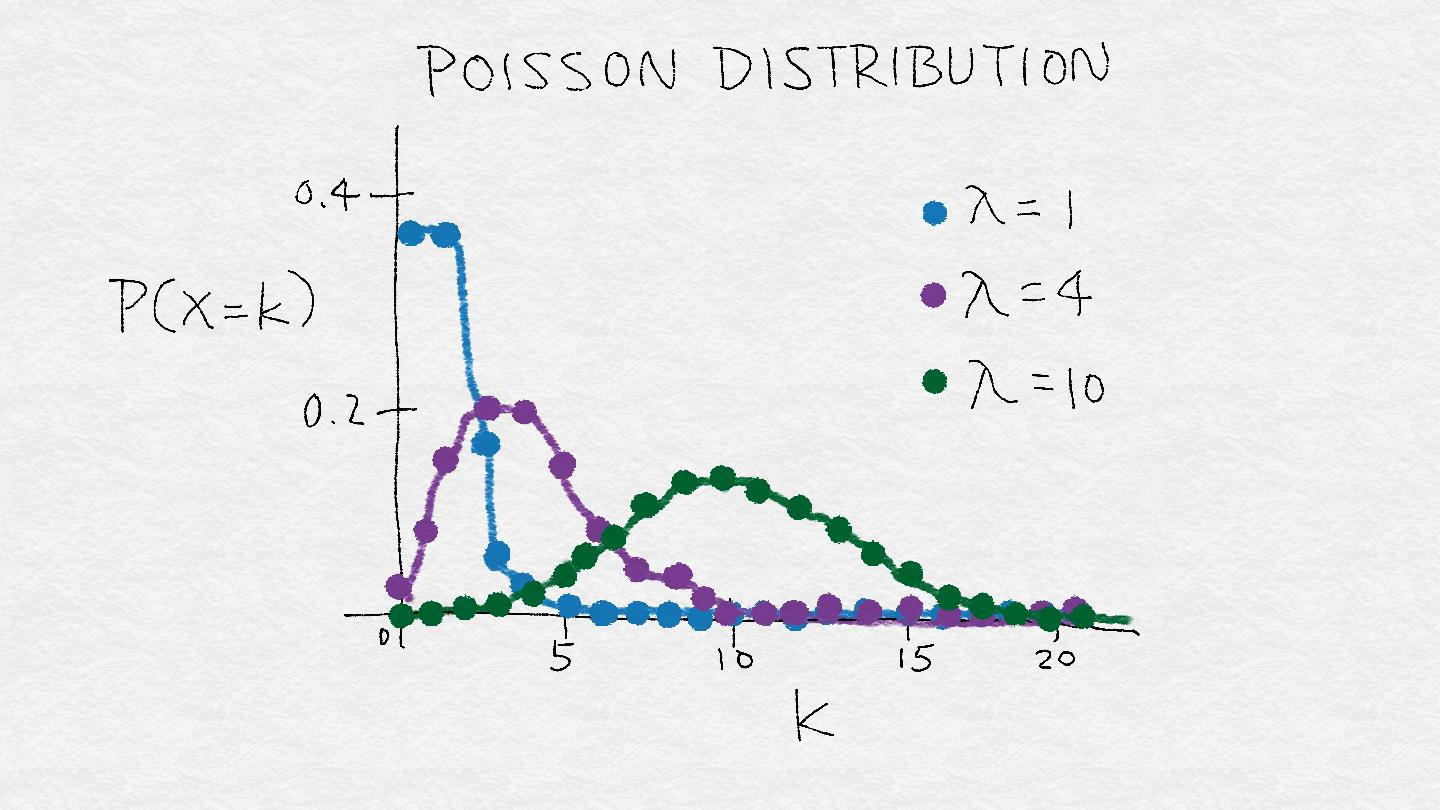 ![](https://img.kancloud.cn/5f/81/5f8199f1ef8211ba3000d790d2872e47_1440x810.png) **Figure 2-11. A rough illustration of the Poisson distribution. λ represents the mean of the distribution. As λ increases, not only does the mode of of the distribution shift to the right, but the mass spreads out and the variance becomes larger. 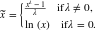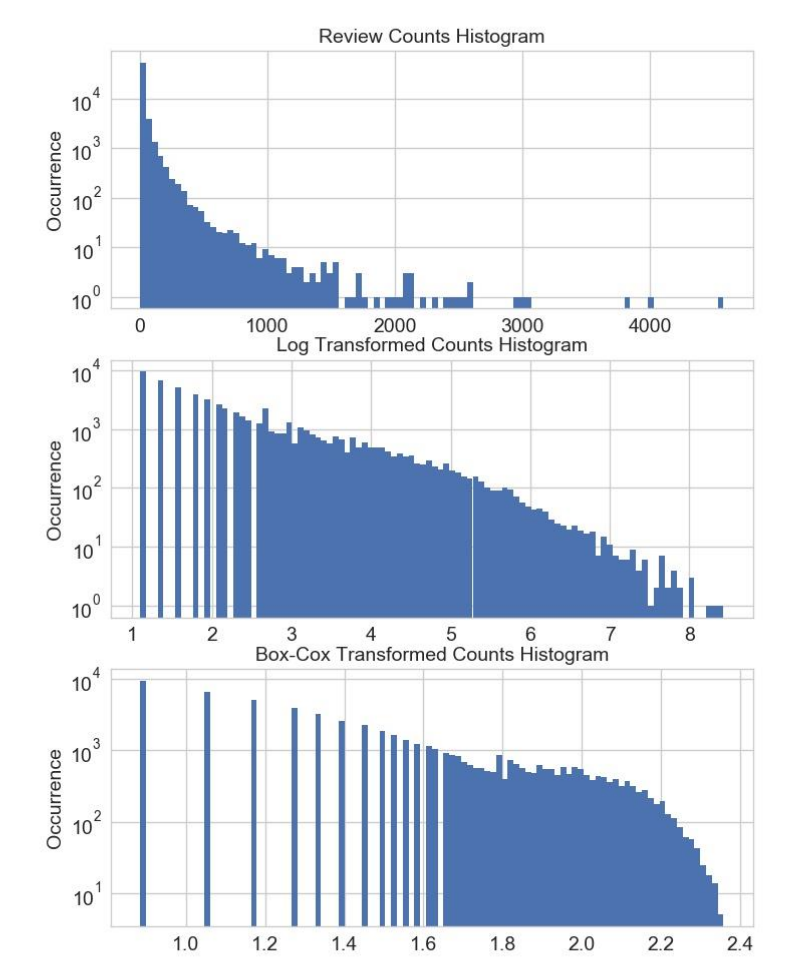The Poisson distribution is an example distribution where the variance increases along with the mean.** 平方根變換和對數變換的簡單推廣稱為Box-Cox變換： ![](https://img.kancloud.cn/fb/ee/fbee5691da696600f77a66ee56bdb7cc_95x30.png) 圖2-12，展示出了在 λ = 0 （log變換），λ = 0.25, λ = 0.5（平方根的縮放和移位版本），λ = 0.75, 和 λ = 1.5 時的Box-Cox變換。設置 λ 小于1時壓縮較高的值，并且設置 λ 大于1時具有相反的效果。 ![](https://img.kancloud.cn/54/69/546923833fee9814f53676136dfd8fc4_924x726.png) **Figure 2-12. Box-Cox transforms for different values of λ.** 只有當數據為正值時, Box-Cox 公式才能工作。對于非正數據, 可以通過加上固定常量來移動數值。當應用 Box-Cox 變換或更一般的功率變換時, 我們必須確定參數 λ 的值。這可能是通過最大似然(找到的λ,使產生的變換信號的高斯似然最大) 或貝葉斯方法。完全介紹 Box-Cox 和一般功率變換的使用超出了本書的范圍。感興趣的讀者可以通過 Jack Johnston 和John DiNardo (McGraw Hill) 編寫的Econometric Methods 找到更多關于冪轉換的信息。幸運的是, Scipy 的數據包包含了一個 Box-Cox 轉換的實現, 其中包括查找最佳變換參數。 ### 例子2-12。Yelp商戶評論數的 Box-Cox 變換。 ``` >>> from scipy import stats # Continuing from the previous example, assume biz_df contains # the Yelp business reviews data # Box-Cox transform assumes that input data is positive. # Check the min to make sure. >>> biz_df['review_count'].min() 3 # Setting input parameter lmbda to 0 gives us the log transform (without constant offset) >>> rc_log = stats.boxcox(biz_df['review_count'], lmbda=0) # By default, the scipy implementation of Box-Cox transform finds the lmbda parameter # that will make the output the closest to a normal distribution >>> rc_bc, bc_params = stats.boxcox(biz_df['review_count']) >>> bc_params -0.4106510862321085 ``` 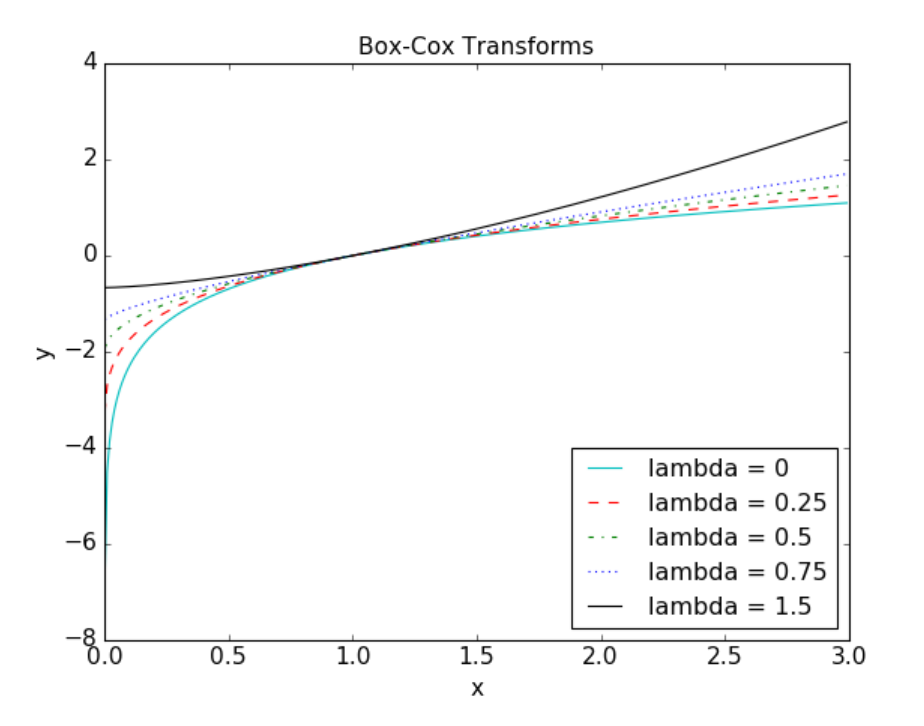圖2-13 提供了原始和轉換評論數分布的可視化比較。 ### 例2-13。可視化評論數的原始、對數轉換和 Box-Cox 轉換的直方圖。 ``` fig, (ax1, ax2, ax3) = plt.subplots(3,1) # original review count histogram biz_df['review_count'].hist(ax=ax1, bins=100) ax1.set_yscale('log') ax1.tick_params(labelsize=14) ax1.set_title('Review Counts Histogram', fontsize=14) ax1.set_xlabel('') ax1.set_ylabel('Occurrence', fontsize=14) # review count after log transform biz_df['rc_log'].hist(ax=ax2, bins=100) ax2.set_yscale('log') ax2.tick_params(labelsize=14) ax2.set_title('Log Transformed Counts Histogram', fontsize=14) ax2.set_xlabel('') ax2.set_ylabel('Occurrence', fontsize=14) # review count after optimal Box-Cox transform biz_df['rc_bc'].hist(ax=ax3, bins=100) ax3.set_yscale('log') ax3.tick_params(labelsize=14) ax3.set_title('Box-Cox Transformed Counts Histogram', fontsize=14) ax3.set_xlabel('') ax3.set_ylabel('Occurrence', fontsize=14) ``` ![](https://img.kancloud.cn/e6/10/e6109ea7bb1d41082893c7f8137ffb73_802x972.png) **Figure 2-13. Box-Cox transformation of Yelp business review counts.** 概率圖是一種直觀地比較數據分布與理論分布的簡單方法。這本質上是觀察到散點圖的與理論分位數。圖2-14顯示YELP評論數的原始數據和轉換后數據相對正態分布的概率圖。由于觀測數據是嚴格正的，高斯可以是負的，所以分位數在負端上永遠不會匹配。所以我們關注的是正數這的一邊。在這方面，原始評論數明顯比正常分布更重尾。（有序值上升到4000，而理論位數僅延伸到4）。簡單的對數變換和最優的 Box-Cox 變換都使正尾部接近正態分布。最優的 Box-Cox 變換比對數變換更縮小尾部，由于尾部在紅色對角線等值線下平展可以明顯看出。 ### 例子 2-14。原始和變換后的數據相對正態分布的概率圖。 ``` fig2, (ax1, ax2, ax3) = plt.subplots(3,1) prob1 = stats.probplot(biz_df['review_count'], dist=stats.norm, plot=ax1) ax1.set_xlabel('') ax1.set_title('Probplot against normal distribution') prob2 = stats.probplot(biz_df['rc_log'], dist=stats.norm, plot=ax2) ax2.set_xlabel('') ax2.set_title('Probplot after log transform') prob3 = stats.probplot(biz_df['rc_bc'], dist=stats.norm, plot=ax3) ax3.set_xlabel('Theoretical quantiles') ax3.set_title('Probplot after Box-Cox transform') ``` ![](https://img.kancloud.cn/88/df/88dfca7fda1634a575471aca48f5cfc5_789x918.png) **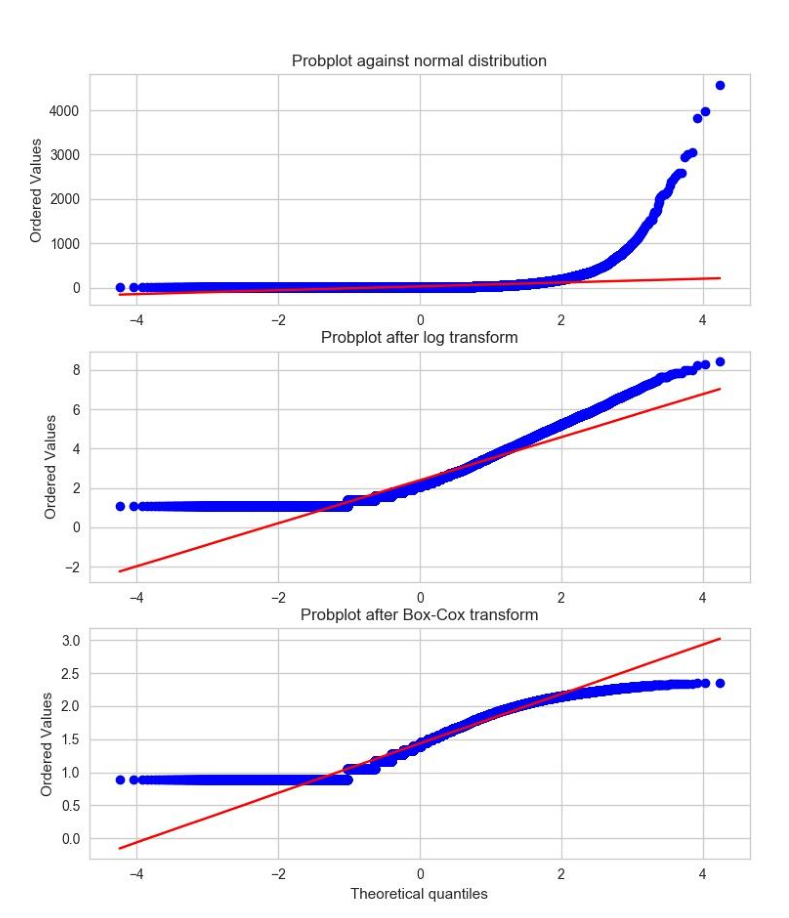Figure 2-14. Comparing the distribution of raw and transformed review counts against the Normal distribution.** ## 特征縮放或歸一化某些特征的值有界的，如緯度或經度。其他數值特征 (如數量) 可能會在無界的情況下增加。那些關于輸入是平滑函數的模型, 如線性回歸、邏輯回歸或任何涉及矩陣的東西, 都受輸入的數值范圍影響。另一方面, 基于樹的模型不太在意這個。如果你的模型對輸入特征的數值范圍敏感, 則特征縮放可能會有所幫助。顧名思義, 特征縮放會更改特征值的數值范圍。有時人們也稱它為特征規范化。功能縮放通常分別針對單個特征進行。有幾種常見的縮放操作, 每個類型都產生不同的特征值分布。 ### Min-max縮放設X是一個單獨的特征值（即，在某些數據點中的一個特征值），以及 min(x) 和 max(x) ，分別是整個數據集上該特征的最小值和最大值。Min-max縮放壓縮（或拉伸）所有特征值到[0, 1 ]的范圍內。圖2-15演示了這個概念。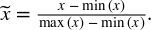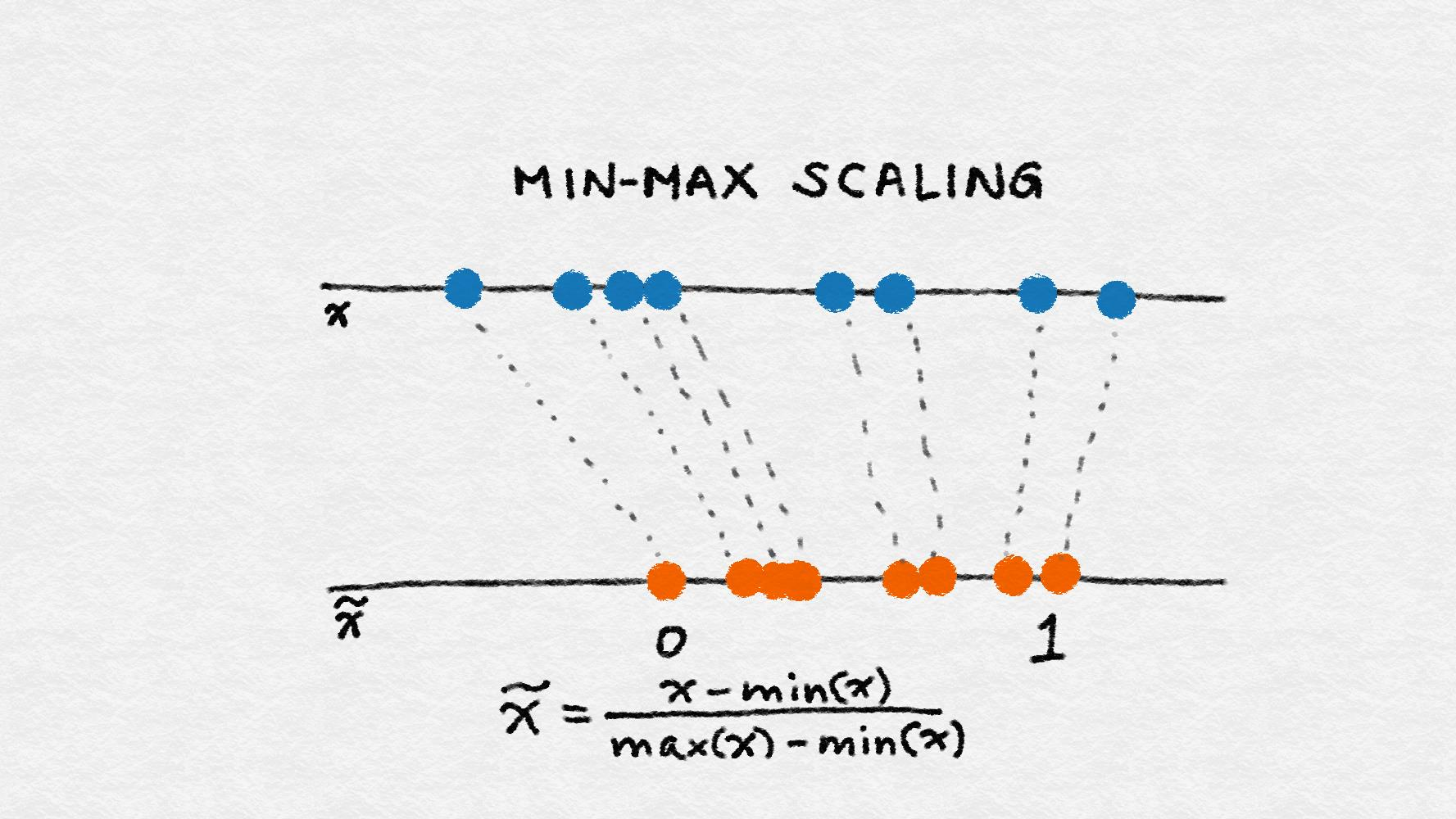最小最大尺度的公式是 ![](https://img.kancloud.cn/03/d8/03d8b359a724d629c01e86e0aeff6f4c_151x30.png) ![](https://img.kancloud.cn/ca/c6/cac693a5d77200a2f25edf8bc51def90_1777x1000.png) **Figure 2-15. 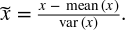Min-max scaling** ### 標準化（方差縮放）特征標準化的定義為： ![](https://img.kancloud.cn/03/4a/034aa4f040ddccf6f2d64be88692e84e_125x30.png) 減去特征 (所有數據點) 的平均值并除以方差。因此, 它也可以稱為方差縮放。縮放后的特征的平均值為0, 方差為1。如果原始特征具有高斯分布, 則縮放特征為標準高斯。圖2-16 包含了標準化的說明。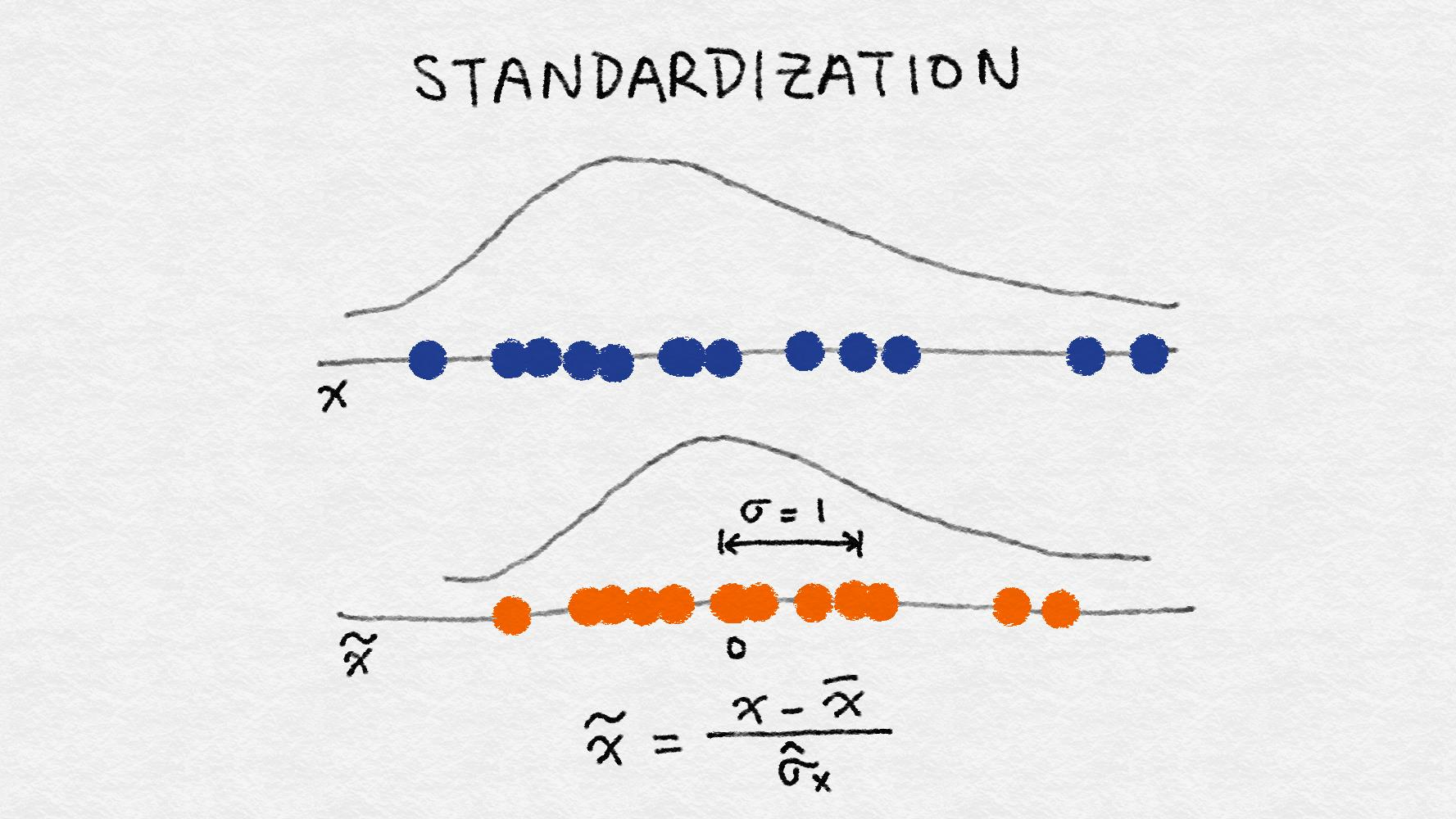 ![](https://img.kancloud.cn/51/8e/518e1895d61d941d5c8f798affdb787d_1777x1000.png) **Figure 2-16. Illustration of feature standardization** ## 不要中心化稀疏數據最小最大縮放和標準化都從原始特征值中減去一個數量。對于最小最大縮放, 移動量是當前特征的所有值中最小的。對于標準化, 移動的量是平均值。如果移動量不是零, 則這兩種轉換可以將稀疏特征（大部分值為零）的向量轉換為一個稠密的向量。這反過來會給分類器帶來巨大的計算負擔, 取決于它是如何實現的。詞袋是一種稀疏表示, 大多數分類庫都對稀疏輸入進行優化。如果現在的表示形式包含了文檔中沒有出現的每個單詞, 那就太可怕了。請謹慎對稀疏特征執行最小最大縮放和標準化操作。 ### L2 normalization 這項技術通過所謂的 L2 范數 (也稱為歐幾里德范數) 正常化 (劃分) 原始特征值。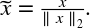 ![](https://img.kancloud.cn/bc/6b/bc6ba3427173f3b567cb16d9d0fb073d_90x28.png) L2范數度量向量在坐標空間中的長度。這個定義可以從眾所周知的勾股定理中得到，給出三角形兩邊的長度，可以得到斜邊長度。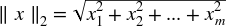 ![](https://img.kancloud.cn/37/d2/37d225eca784fb437bbaba615b53126d_226x28.png) L2 范數將求特征的各數據點的平方和, 然后取平方根。L2 規范化后, 該特征列具有范數1。它也可以稱為 L2 縮放。(不嚴謹的說, 縮放意味著和常量相乘, 而規范化可能涉及許多操作。）圖2-17說明了 L2 規范化。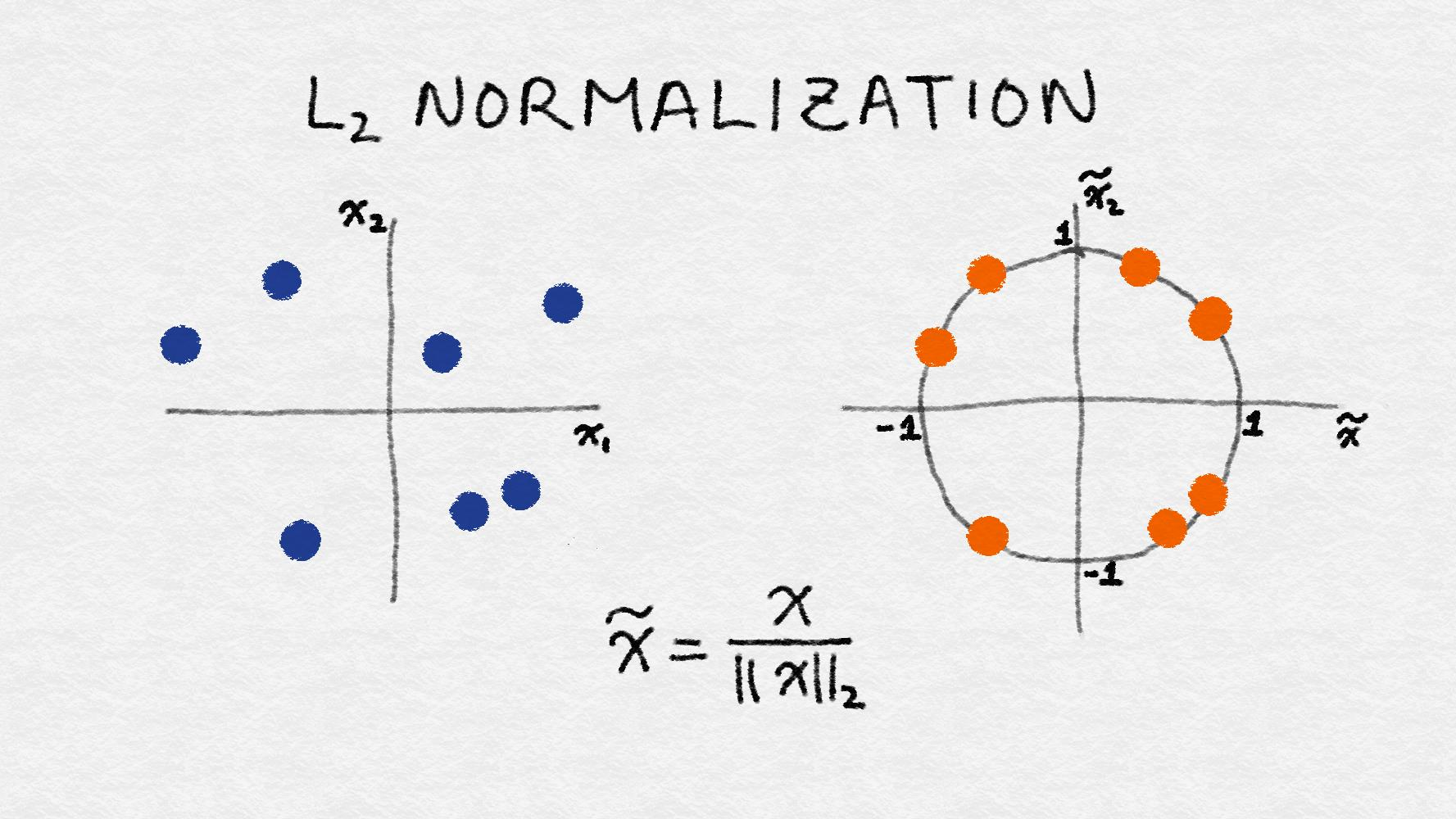 ![](https://img.kancloud.cn/5a/38/5a3887228b2e3ecbe3de322ba7badb07_1777x1000.png) **Figure 2-17. Illustration of L2 feature normalization** ## 數據空間與特征空間請注意，圖2-17中的說明是在數據空間中，而不是特征空間。還可以對數據點進行L2歸一化，而不是特征，這將導致具有單位范數（范數為1）的數據向量。（參見[詞袋](https://www.safaribooksonline.com/library/view/feature-engineering-for/9781491953235/ch03.html#sec-bag-of-words)中關于數據向量和特征向量的互補性質的討論）不管縮放方法如何，特征縮放總是將特征除以常數（也稱為歸一化常數）。因此，它不會改變單特征分布的形狀。我們將用在線新聞文章標記計數來說明這一點。 ### 例子 2-15。特征縮放示例。 ``` >>> import pandas as pd >>> import sklearn.preprocessing as preproc # Load the online news popularity dataset >>> df = pd.read_csv('OnlineNewsPopularity.csv', delimiter=', ') # Look at the original data - the number of words in an article >>> df['n_tokens_content'].as_matrix() array([ 219., 255., 211., ..., 442., 682., 157.]) # Min-max scaling >>> df['minmax'] = preproc.minmax_scale(df[['n_tokens_content']]) >>> df['minmax'].as_matrix() array([ 0.02584376, 0.03009205, 0.02489969, ..., 0.05215955, 0.08048147, 0.01852726]) # Standardization - note that by definition, some outputs will be negative >>> df['standardized'] = preproc.StandardScaler().fit_transform(df[['n_tokens_content']]) >>> df['standardized'].as_matrix() array([-0.69521045, -0.61879381, -0.71219192, ..., -0.2218518 , 0.28759248, -0.82681689]) # L2-normalization >>> df['l2_normalized'] = preproc.normalize(df[['n_tokens_content']], axis=0) >>> df['l2_normalized'].as_matrix() array([ 0.00152439, 0.00177498, 0.00146871, ..., 0.00307663, 0.0047472 , 0.00109283]) ``` 我們也可以可視化用不同的特征縮放方法后的數據的分布。如圖2-18所示，與對數變換不同，特征縮放不會改變分布的形狀；只有數據的規模發生變化。 ### 例2-16。繪制原始數據和縮放數據的直方圖。 ``` >>> fig, (ax1, ax2, ax3, ax4) = plt.subplots(4,1) >>> fig.tight_layout() >>> df['n_tokens_content'].hist(ax=ax1, bins=100) >>> ax1.tick_params(labelsize=14) >>> ax1.set_xlabel('Article word count', fontsize=14) >>> ax1.set_ylabel('Number of articles', fontsize=14) >>> df['minmax'].hist(ax=ax2, bins=100) >>> ax2.tick_params(labelsize=14) >>> ax2.set_xlabel('Min-max scaled word count', fontsize=14) >>> ax2.set_ylabel('Number of articles', fontsize=14) >>> df['standardized'].hist(ax=ax3, bins=100) >>> ax3.tick_params(labelsize=14) >>> ax3.set_xlabel('Standardized word count', fontsize=14) >>> ax3.set_ylabel('Number of articles', fontsize=14) >>> df['l2_normalized'].hist(ax=ax4, bins=100) >>> ax4.tick_params(labelsize=14) >>> ax4.set_xlabel('L2-normalized word count', fontsize=14) >>> ax4.set_ylabel('Number of articles', fontsize=14) ``` ![](https://img.kancloud.cn/38/65/386569131688412b7d42e981f9aa2f3a_888x615.png) **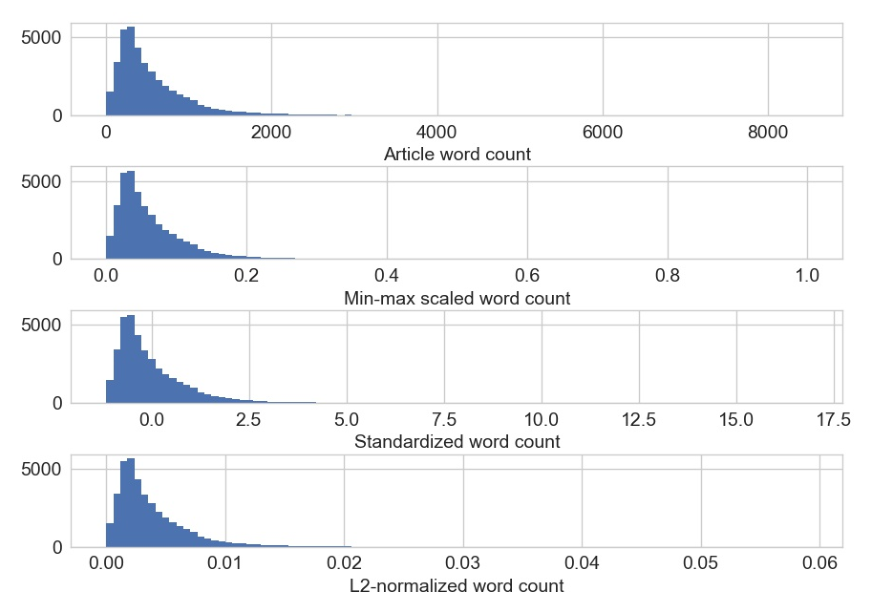Figure 2-18. Original and scaled news article word counts. Note that only the scale of the x-axis changes; the shape of the distribution stays the same with feature scaling.** 在一組輸入特征在比例上差異很大的情況下，特征縮放非常有用。例如，一個流行的電子商務網站的每日訪問者數量可能是十萬，而實際銷售額可能是幾千。如果這兩種功能都投入到模型中，那么該模型需要在確定要做什么的同時平衡它們的規模。輸入特征的極大變化會導致模型訓練算法的數值穩定性問題。在這些情況下，標準化功能是個好主意。第4章將詳細介紹處理自然文本時的特征縮放，包括使用示例。 ## 交互特征簡單的成對交互特征是兩個特征的積。類似邏輯與。它以成對條件表示結果：“購買來自郵政編碼98121”和“用戶的年齡在18到35之間”。這一點對基于決策樹的模型沒有影響，但發交互特征對廣義線性模型通常很有幫助。一個簡單的線性模型使用單個輸入特征線性組合x1，x2，... 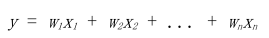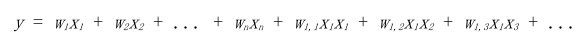xn來預測結果y ![](https://img.kancloud.cn/52/c7/52c7fbf9c11eafae2f2393f4546c6df8_269x38.png) 一個簡單的擴展線性模型的方法是包含輸入特征對的組合，如下所示： ![](https://img.kancloud.cn/84/af/84af440486c197d39b495ab05a2b0b00_584x40.png) 這使我們能夠捕獲特征之間的相互影響，因此它們被稱為交互特征。如果x1和x2是二元的，那么它們的積 x1x2 是邏輯函數 x1 AND x2 假設問題是根據他或她的個人資料信息預測客戶的偏好。在這種情況下，交互特征不是僅基于用戶的年齡或位置進行預測，而交互特征允許模型基于具有特定年齡和特定位置的用戶進行預測。在例2-17中，我們使用 UCI 在線新聞數據集中的成對交互特征來預測每篇新聞文章的分享數量。交互特征導致精度超過單身特征。兩者都比例2-9表現得更好，它使用文章正文中單詞數的單個預測器（有或沒有經過對數變換）。 ### 例子 2--17。用于預測的交互特征示例。 ``` >>> from sklearn import linear_model >>> from sklearn.model_selection import train_test_split >>> import sklearn.preprocessing as preproc ### Assume df is a Pandas dataframe containing the UCI online news dataset >>> df.columns Index(['url', 'timedelta', 'n_tokens_title', 'n_tokens_content', 'n_unique_tokens', 'n_non_stop_words', 'n_non_stop_unique_tokens', 'num_hrefs', 'num_self_hrefs', 'num_imgs', 'num_videos', 'average_token_length', 'num_keywords', 'data_channel_is_lifestyle', 'data_channel_is_entertainment', 'data_channel_is_bus', 'data_channel_is_socmed', 'data_channel_is_tech', 'data_channel_is_world', 'kw_min_min', 'kw_max_min', 'kw_avg_min', 'kw_min_max', 'kw_max_max', 'kw_avg_max', 'kw_min_avg', 'kw_max_avg', 'kw_avg_avg', 'self_reference_min_shares', 'self_reference_max_shares', 'self_reference_avg_sharess', 'weekday_is_monday', 'weekday_is_tuesday', 'weekday_is_wednesday', 'weekday_is_thursday', 'weekday_is_friday', 'weekday_is_saturday', 'weekday_is_sunday', 'is_weekend', 'LDA_00', 'LDA_01', 'LDA_02', 'LDA_03', 'LDA_04', 'global_subjectivity', 'global_sentiment_polarity', 'global_rate_positive_words', 'global_rate_negative_words', 'rate_positive_words', 'rate_negative_words', 'avg_positive_polarity', 'min_positive_polarity', 'max_positive_polarity', 'avg_negative_polarity', 'min_negative_polarity', 'max_negative_polarity', 'title_subjectivity', 'title_sentiment_polarity', 'abs_title_subjectivity', 'abs_title_sentiment_polarity', 'shares'], dtype='object') ### Select the content-based features as singleton features in the model, ### skipping over the derived features features = ['n_tokens_title', 'n_tokens_content', 'n_unique_tokens', 'n_non_stop_words', 'n_non_stop_unique_tokens', 'num_hrefs', 'num_self_hrefs', 'num_imgs', 'num_videos', 'average_token_length', 'num_keywords', 'data_channel_is_lifestyle', 'data_channel_is_entertainment', 'data_channel_is_bus', 'data_channel_is_socmed', 'data_channel_is_tech', 'data_channel_is_world'] >>> X = df[features] >>> y = df[['shares']] ### Create pairwise interaction features, skipping the constant bias term >>> X2 = preproc.PolynomialFeatures(include_bias=False).fit_transform(X) >>> X2.shape (39644, 170) ### Create train/test sets for both feature sets >>> X1_train, X1_test, X2_train, X2_test, y_train, y_test = train_test_split(X, X2, y, test_size=0.3, random_state=123) >>> def evaluate_feature(X_train, X_test, y_train, y_test): ... '''Fit a linear regression model on the training set and score on the test set''' ... model = linear_model.LinearRegression().fit(X_train, y_train) ... r_score = model.score(X_test, y_test) ... return (model, r_score) ### Train models and compare score on the two feature sets >>> (m1, r1) = evaluate_feature(X1_train, X1_test, y_train, y_test) >>> (m2, r2) = evaluate_feature(X2_train, X2_test, y_train, y_test) >>> print("R-squared score with singleton features: %0.5f" % r1) >>> print("R-squared score with pairwise features: %0.10f" % r2) R-squared score with singleton features: 0.00924 R-squared score with pairwise features: 0.0113276523 ``` 構造交互特征非常簡單，但它們使用起來很昂貴。使用成對交互特征的線性模型的訓練和得分時間將從O（n）到O（n2），其中n是單身特征的數量。圍繞高階交互特征的計算成本有幾種方法。可以在所有交互特征之上執行特征選擇，選擇前幾個。或者，可以更仔細地制作更少數量的復雜特征。兩種策略都有其優點和缺點。特征選擇采用計算手段來選擇問題的最佳特征。（這種技術不限于交互特征。）一些特征選擇技術仍然需要訓練多個具有大量特征的模型。手工制作的復雜特征可以具有足夠的表現力，所以只需要少量這些特征，這可以縮短模型的訓練時間。但是特征本身的計算可能很昂貴，這增加了模型評分階段的計算成本。手工制作（或機器學習）的復雜特征的好例子可以在第8章有關圖像特征中找到。現在讓我們看看一些特征選擇技巧。 ## 特征選擇特征選擇技術會刪除非有用的特征，以降低最終模型的復雜性。最終目標是快速計算的簡約模型，預測準確性降低很小或不會降低。為了得到這樣的模型，一些特征選擇技術需要訓練多個候選模型。換句話說，特征選擇并不是減少訓練時間，實際上有些技巧增加了整體訓練時間，但是減少了模型評分時間。粗略地說，特征選擇技術分為三類。 Filtering（過濾）: 預處理可以刪除那些不太可能對模型有用的特征。例如，可以計算每個特征與響應變量之間的相關或相互信息，并篩除相關信息或相互信息低于閾值的特征。第3章討論了文本特征的過濾技術的例子。過濾比下面的包裝（wrapper）技術便宜得多，但是他們沒有考慮到正在使用的模型。因此他們可能無法為模型選擇正確的特征。最好先保守地進行預過濾，以免在進行模型訓練步驟之前無意中消除有用的特征。 Wrapper methods（包裝方法）：這些技術是昂貴的，但它們允許您嘗試特征子集，這意味著你不會意外刪除自身無法提供信息但在組合使用時非常有用的特征。包裝方法將模型視為提供特征子集質量分數的黑盒子。shi一個獨立的方法迭代地改進子集。 Embedded methods（嵌入式方法）：嵌入式方法執行特征選擇作為模型訓練過程的一部分。例如，決策樹固有地執行特征選擇，因為它在每個訓練步驟選擇一個要在其上進行樹分裂的特征。另一個例子是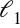![](https://img.kancloud.cn/8e/9e/8e9ead95aaed48f120653fab5ec0695d_20x28.png)正則，它可以添加到任何線性模型的訓練目標中。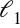![](https://img.kancloud.cn/8e/9e/8e9ead95aaed48f120653fab5ec0695d_20x28.png)鼓勵模型使用一些特征而不是許多特征。因此它也被稱為模型的稀疏約束。嵌入式方法將特征選擇作為模型訓練過程的一部分。它們不如包裝方法那么強大，但也遠不如包裝方法那么昂貴。與過濾相比，嵌入式方法會選擇特定于模型的特征。從這個意義上講，嵌入式方法在計算費用和結果質量之間取得平衡。特征選擇的全面處理超出了本書的范圍。有興趣的讀者可以參考 Isabelle Guyon 和 André Elisseeff 撰寫的調查報告“變量和特征選擇介紹”（“An Introduction to Variable and Feature Selection”）。 ## 總結本章討論了許多常見的數字特征工程技術：量化，縮放（又稱規范化），對數變換（一種功率變換），交互特征以及處理大量交互特征所需的特征選擇技術的簡要總結。在統計機器學習中，所有數據最終歸結為數字特征。因此，所有道路最終都會指向某種數字特征工程技術。為了結束特征工程這個游戲，保證這些工具方便使用！ ## 參考書目 Guyon, Isabell, and André Elisseeff. 2003. Journal of Machine Learning Research Special Issue on Variable and Feature Selection. 3(Mar):1157--1182. Johnston, Jack, and John DiNardo. 1997. Econometric Methods (Fourth Edition). New York: McGraw Hill.