# 附錄、線性模型和線性代數基
> 譯者:[@Sherlock-kid](https://github.com/Sherlock-kid)
## 線性分類概述
當我們有一個已經標記的數據集時,特征空間散布著來自不同類別的數據點。分類器的工作是將不同類別的數據點分開。它可以通過生成一個數據點與另一個數據點非常不同的輸出來實現。例如,當這里只有兩個類別的時候,一個好的分類器應該為一個類別產生大量的輸出,而另一個則為小的輸出。作為一個類別而不是另一個類別的點就形成了一個決策平面。
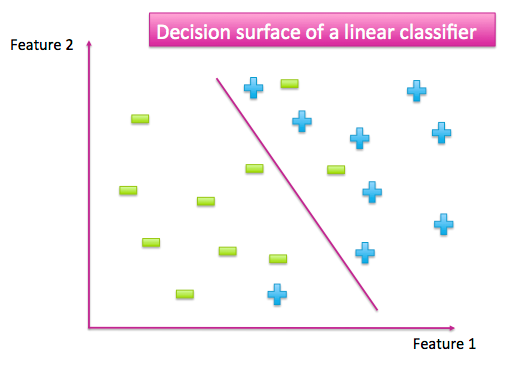
圖 A-1:簡單的二元分類找到了一個分離兩類數據點的曲面
許多函數能被當作分類器。這是一個尋找能完全分離不同類的簡單函數的好方法。首先,相比于尋找最復雜的分類器,尋找最簡單的分類器更容易。而且,簡單函數常常能更好地適應新數據,要將它們與訓練數據(特別是過度擬合)相比。一個簡單的模型也許會出錯,就像上圖一些數據點被分到了錯誤的一邊。但是我們犧牲了一些訓練的準確性,以便有一個更簡單的決策平面,可以達到更好的測試精度。最大限度減少復雜性和最大限度增加精度被叫做“奧卡姆剃刀”,廣泛適用于科學與工程。
最簡單的函數是一條直線。一個一元線性函數是我們最熟悉的。
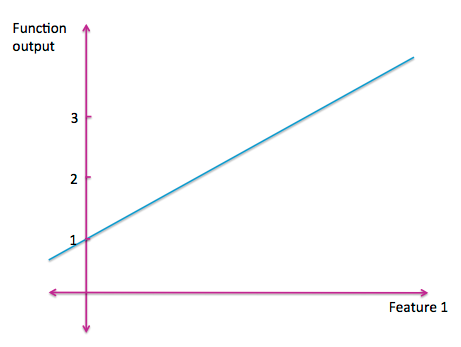
圖 A-2:一元線性函數
二元線性函數可以顯示為 3D 中的平面或 2D 中的等高線圖(如圖 A-3)。與拓撲地理圖一樣,等高線圖的每一行代表輸入空間中具有相同輸出的點。
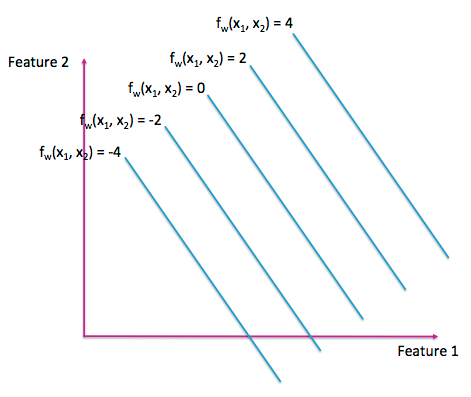
圖 A-3:二維線性函數的等高線圖
可視化更高維度的線性函數很難,它們被稱作超平面。但是寫出它們的代數公式還是很容易的。一個多維的線性模型有一個輸入集合`x1,x2,…,xn`和一個權重參數集合`w0,w1,…,wn`:`fw(x1,x2,…,xn) = w0+w1*x1+w2*x2+…+wn*xn`。這個公式能被寫成更簡潔的向量形式 $fw(X)=X^T W$。 我們遵循通常的數學符號慣例,它使用粗體來表示一個向量和非粗體來表示一個標量。向量`x`在開始處用一個額外的 1 填充,作為截距項`w0`的占位符。如果所有輸入特征都為零,那么函數的輸出是`w0`。 所以`w0`也被稱為偏差或截距項。
訓練線性分類器相當于在類之間挑出最佳分離超平面。這意味著找到在空間中精確定位的最佳矢量`w`。由于每個數據點都有一個目標標簽`y`,我們可以找到一個`w`,它試圖直接模擬目標的標簽 $x^T w=y$。
由于通常有多個數據點,我們需要一個`w`同時使所有的預測都接近目標標簽:
方程 A-1:線性模型公式`Aw=y`
這里,`A`被稱為數據矩陣(在統計中也被稱為設計矩陣)。它包含特定形式的數據:每行是數據點,每列都是一個特征。(有時人們也會看到它的轉置,其中的特征以行的形式顯示,數據以列的形式顯示。)
## 矩陣的解析
為了解決方程 A-1,我們需要一些線性代數的基本知識。為了系統地介紹這個主題,我們強烈推薦 Gilbert Strang 的書《Linear Algebra and Its Applications》(線性代數及其應用)。
方程 A-1 指出,當某個矩陣乘以某個向量時,會有一定的結果。一個矩陣也被叫做一個線性算子,這個名稱使得矩陣更像一臺小機器。該機器將一個矢量作為輸入,并使用多個關鍵操作的組合來推導出另一個矢量:一個矢量方向的旋轉,添加或減去維度,以及拉伸或壓縮其長度。這種組合在輸入空間中操縱形狀時非常有用(見圖 A-4)。
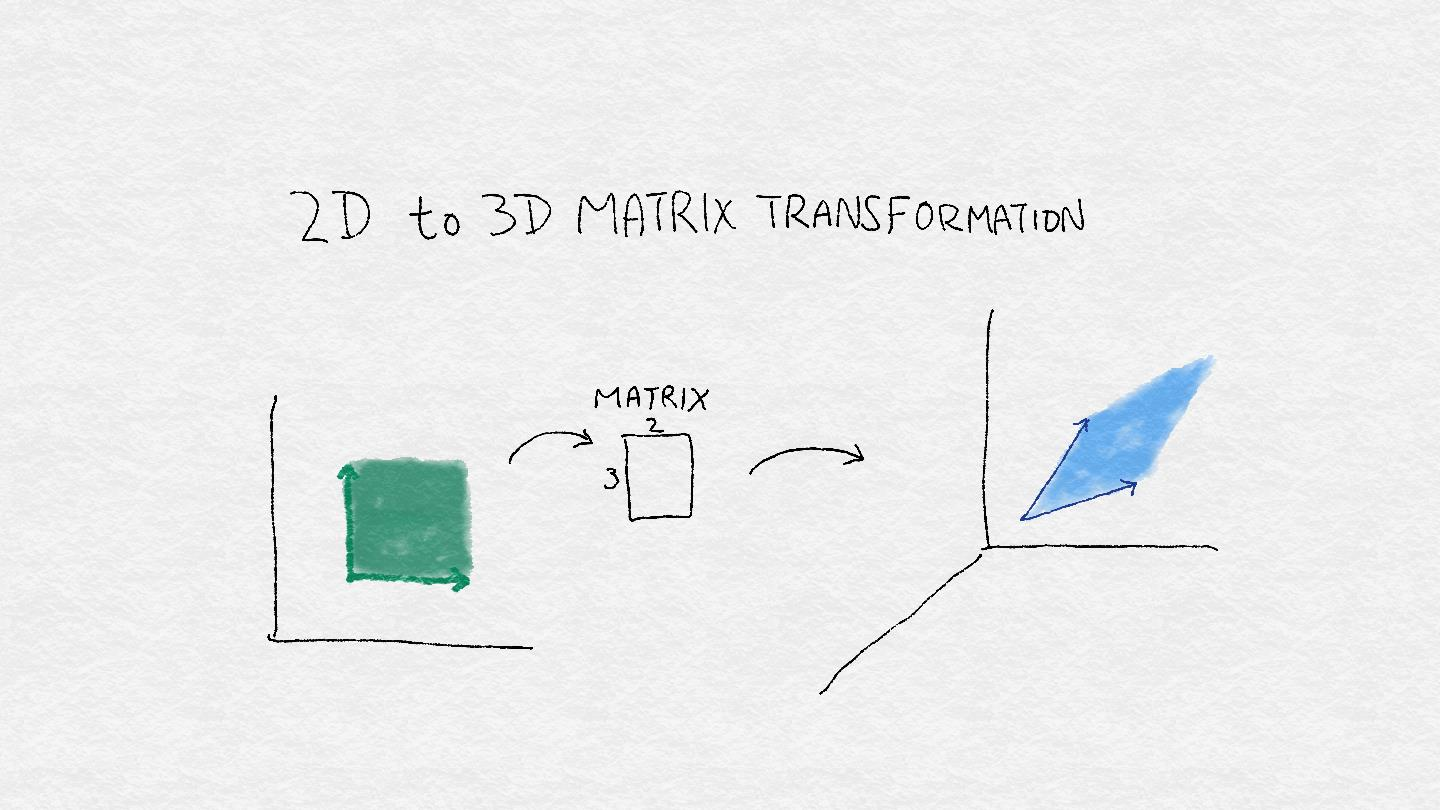
圖 A-4:`3 x 2`矩陣可以將 2D 中的正方形區域轉換為 3D 中的菱形區域。 它通過將輸入空間中的每個向量旋轉并拉伸到輸出空間中的新向量來實現。
## 從矢量到子空間
為了理解線性算子,我們必須看看它如何將輸入變為輸出。幸運的是,我們不必一次分析一個輸入向量。向量可以組織成子空間,而線性算子則可以處理向量子空間。子空間是一組滿足兩個標準的向量:(1)如果它包含一個向量,那么它包含通過原點和該點的直線,以及(2)如果它包含兩個點,則它包含所有線性組合 的這兩個向量。 線性組合是兩種操作類型的組合:將矢量與標量相乘,并將兩個矢量相加在一起。
子空間的一個重要屬性是它的秩或維度,它是這個空間中自由度的度量。一條線的秩為 1,2D 平面的秩為 2,依此類推。如果你可以想象在我們的多維空間中的多維鳥,那么子空間的秩告訴我們鳥可以飛行多少個“獨立”的方向。這里的“獨立”意思是“線性獨立性”:如果一個不是另一個的常數倍,那么兩個向量是線性獨立的,即它們并不指向完全相同或相反的方向。
子空間可以被定義為一組基向量的范圍。(跨度是描述一組向量的所有線性組合的技術術語。)一組向量的跨度在線性組合下是不變的(因為它是以這種方式定義的)。因此,如果我們有一組基向量,那么我們可以將這些向量乘以任何非零常數或者添加向量來獲得另一個基。
有一個更獨特和可識別的基來描述一個子空間將是很好的。標準正交基包含具有單位長度且彼此正交的矢量。正交性是另一個技術術語。(所有數學和科學中至少有50%是由技術術語組成的,如果你不相信我,請在本書中做一個袋裝詞)。如果兩個向量的內積是 零。 對于所有密集的目的,我們可以將正交矢量看作相互成 90 度角。(這在歐幾里得空間中是真實的,這與我們的物理三維現實非常相似。)將這些向量標準化為單位長度將它們變成一組統一的測量棒。
總而言之,一個子空間就像一個帳篷,正交基矢量是支撐帳篷所需的直角桿數。秩等于正交基向量的總數。
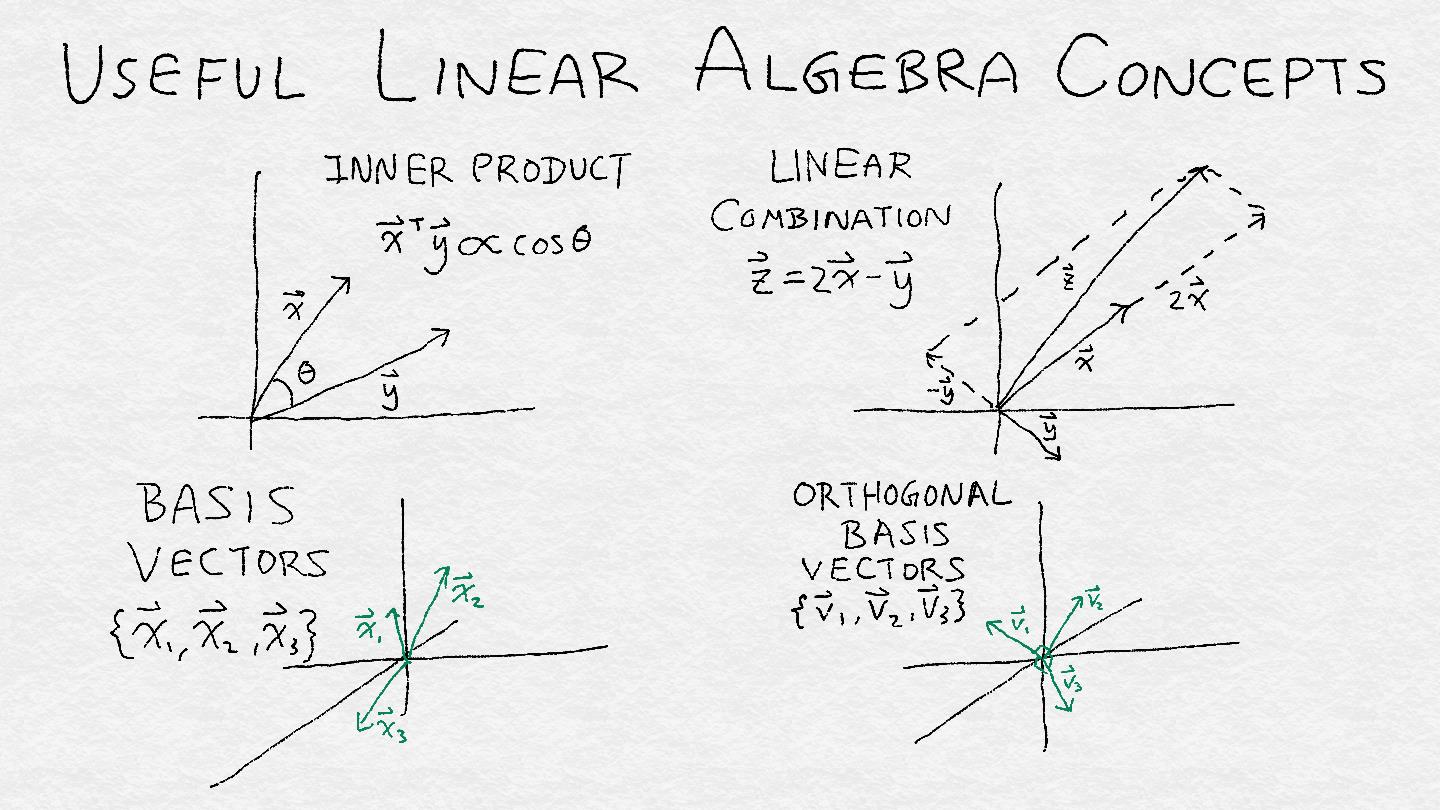
圖 A-5:四個有用的線性代數概念的插圖:內積,線性組合,基向量和正交基向量。
對于那些在數學中思考的人來說,這里有一些數學來描述我們的描述。
#### 有用的線性代數定義
+ 標量:一個數`c`,不是矢量
+ 向量:$x=(x_1,x_2,…,x_n)$
+ 線性組合:$ax+by=ax_1+by_1,ax_2+by_2,…,ax_n+by_n$
+ 向量組的范圍:向量組 $u=a_1 v_1+?+a_k v_k$,$a_1,…,a_k$ 任意
+ 線性獨立性:`x`和`y`相互獨立,如果`x≠cy`,`c`是任何標量常量
+ 內在產品:$x,y=x_1 y_1+x_2 y_2+?+x_n y_n$
+ 正交矢量:如果`x,y=0`,兩個向量`x,y`正交
+ 子空間:包含更大的矢量空間中的矢量子集,滿足這三個標準:
+ 包含 0 向量
+ 如果包含一個向量`v`,那么也包含所有向量`cv`,其中`c`是一個標量。
+ 如果包含兩個向量`u`和`v`,那么也包含`u+v`
+ 基:一組跨向子空間的向量
+ 正交基:一個基 ${v_1,v_2,…,v_d}$,$v_i,v_j=0$,`i,j`任意
+ 子空間的秩:跨越子空間的線性無關基向量的最小數目。
+
## 奇異值分解(SVD)
矩陣對輸入向量執行線性變換。線性變換非常簡單且受到限制。因此,矩陣不能無情地操縱子空間。線性代數最迷人的定理之一證明了每一個方陣,無論它包含什么數字,都必須將某一組矢量映射回自己,并進行一些縮放。在矩形矩陣的一般情況下,它將一組輸入向量映射為相應的一組輸出向量,其轉置將這些輸出映射回原始輸入。技術術語是正方形矩陣具有特征值的特征向量,矩形矩陣具有奇異值的左右奇異向量。
#### 特征向量和奇異向量
設`A`是一個`n*n`的矩陣。如果這里有一個向量`v`和一個標量`λ`,使`Av=λv`,`v`稱作特征向量,`λ`稱為`A`的一個特征值。
讓`A`成為一個長方形矩陣。如果這里有一個向量`u`和一個向量`v`和一個標量`σ`,那么`Av=σu`,$A^T u=σv$,`u`和`v`被叫做左右奇異向量,`σ`是`A`的奇異值。
代數上,矩陣的 SVD 看起來像這樣:
$A=U \Sigma V^T$
其中矩陣`U`和`V`的列分別形成輸入和輸出空間的正交基。`Σ`是一個一個包含奇異值的對角矩陣。
在幾何學上,矩陣執行以下的變換序列(見圖 A-6):
+ 將輸入向量映射到右奇異向量基V上
+ 通過相應的奇異值縮放每個坐標
+ 將此分數與每個左奇異向量相乘
+ 總結結果
當`A`是實矩陣(即所有元素都是實值)時,所有的奇異值和奇異向量都是實值的。奇異值可以是正數,負數或零。矩陣的有序奇異值集稱為譜,它揭示了很多矩陣。奇異值之間的差距會影響解的穩定性,最大絕對奇異值與最小絕對奇異值之間的比值(條件數)會影響迭代求解器的求解速度。這兩個屬性都對可找到的解決方案的質量產生顯著影響。
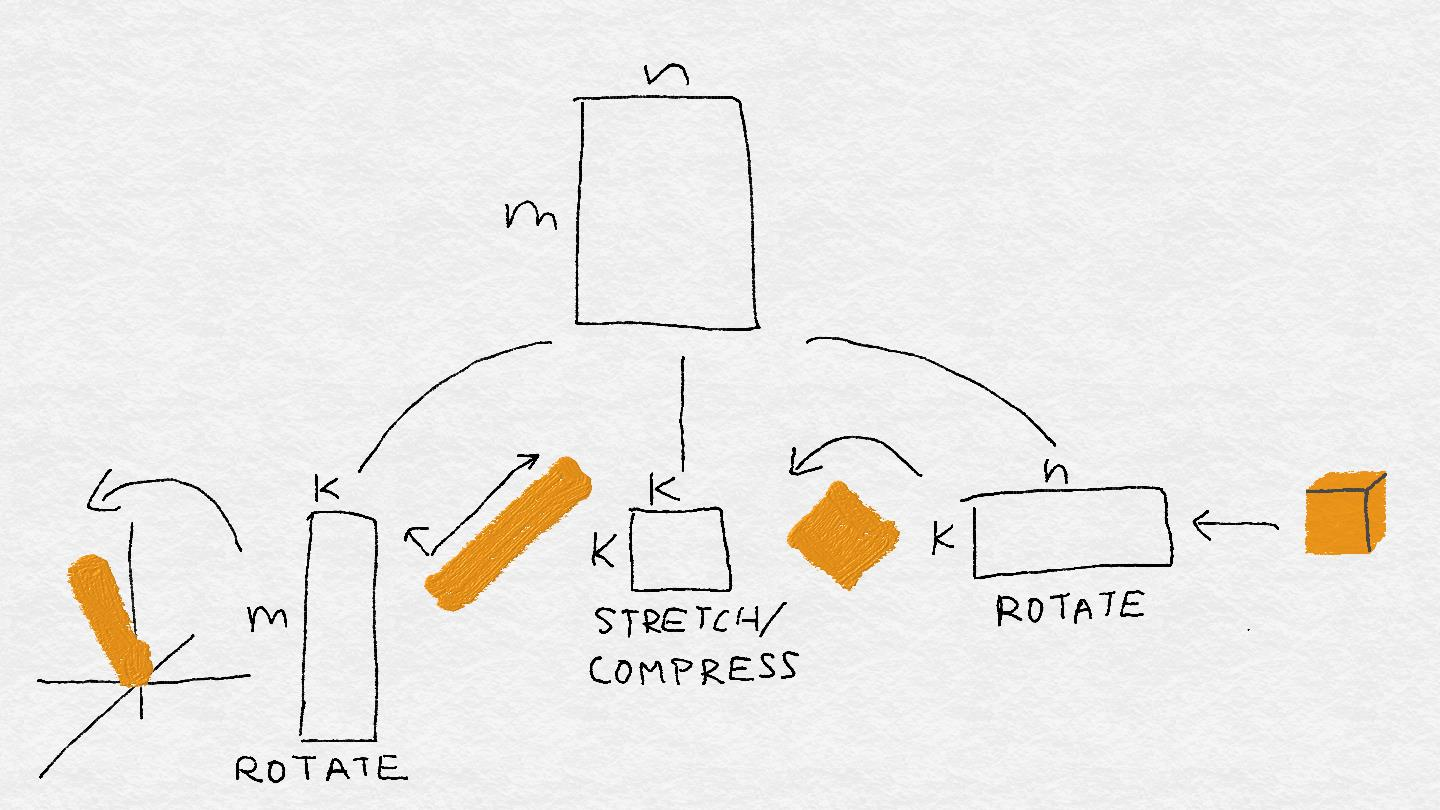
圖 A-6:矩陣分解成三個小機器:旋轉,縮放,旋轉。
操作從右到左進行矩陣向量乘法。最右邊的機器旋轉并潛在地將輸入投影到較低維空間中。在這個例子中,輸入立方體變成了一個扁平的正方形,并且也被旋轉了。下一臺機器在一個方向擠壓正方形,并將其拉伸到另一個方向;正方形變成矩形。最后一個最左邊的機器再次旋轉矩形,并將其投影回可能更高的空間。但它仍然是一個扁平的矩形,而不是一些更高維的對象。
## 數據矩陣的四個基本子空間
解析矩陣的另一種有用方法是通過四個基本子空間:列空間,行空間,右空間和左空間。這四個子空間完全刻畫了涉及`A`或 $A^T$ 的線性系統的解決方案。因此它們被稱為四個基本子空間。對于數據矩陣,可以根據數據和特征理解四個基本子空間。讓我們更詳細地看看它們。
#### 數據矩陣
`A`:行是數據點,列是特征。
### 列空間
數學定義:
當我們改變權值向量`w`時,輸出向量`s`的集合,其中`s=Aw`
數學解釋:
所有可能的列的組合。
數據解釋:
根據觀察到的特征,所有結果都是線性可預測的,向量`w`包含每個特征的權重。
基本原理:
對應非零奇異值的左奇異向量(`U`列的子集)。
### 行空間
數學定義:
當我們改變權值向量`u`時,輸出向量的集合 $r=u^T A$
數學解釋:
所有可能的行線性組合
數據解釋:
行空間中的向量可以表示為現有數據點的線性組合。因此,這可以解釋為已有數據的空間。向量`u`包含線性組合中每個數據點的權重。
基本原理:
對應非零奇異值的右奇異向量(`V`列的子集)
### 零空間
數學定義:
輸入向量`w`的集合,其中`Aw=0`。
數學解釋:
正交于`A`的所有行的向量。零空間被矩陣壓縮為 0。這是“fluff”,它增加了`Aw=y`的解空間的體積。
數據解釋:
新數據點,它不能被表示為現有數據點的任何線性組合
基本原理:
對應零奇異值的右奇異向量(`V`的其余列)
### 左零空間
數學定義:
輸入向量`u`的集合,其中 $u^T A=0$
數學解釋:
正交于`A`的所有列的向量。左零空間正交于列空間。
數據解釋:
不能用現有特征的線性組合來表示的新特征向量。
基本原理:
對應零奇異值的左奇異向量(`U`的其余列)
列空間和行空間包含根據觀察到的數據和特性所能表示的內容。列空間中的這些向量是非新特征。那些位于行空間中向量都是非新的數據點。
對于建模和預測的目的,非新奇性是好的。完整的列空間意味著特征集包含足夠的信息來建模我們的任何目標向量的愿望。一個完整的行空間意味著不同的數據點包含足夠的變化來覆蓋特性空間的所有可能的角落。我們要擔心的是新的數據點和特征,它們分別包含在零空間和左零空間中。
在建立數據線性模型的應用,零空間中也可以看作是“新”數據點的子空間。在這種情況下,新奇并不是一件好事。新數據點是訓練集不能線性表示的虛數據,同樣,左零空間包含的新特征不能用現有特征的線性組合表示。
零空間正交于行空間。原因很簡單,零空間的定義是`w`的內積為 0,每一個行向量都是`A`。因此,`w`正交于由這些行向量張成的空間即行空間。類似地,左零空間正交于列空間。
### 求解一個線性系統
讓我們把所有這些數學問題都歸結到手頭的問題上:訓練一個線性分類器,它與解決線性系統的任務密切相關。我們仔細看一個矩陣是如何運作的,因為我們要逆向設計它。為了建立一個線性模型,我們必須找到輸入權向量`w`映射到觀察到的輸出目標`y`在系統`Aw=y`,其中`A`是數據矩陣。讓我們試著把線性算子的機器反過來轉動。如果我們有`A`的 SVD 分解,那么我們可以把`y`映射到左奇異向量(`U`的列),反轉比例因子(乘以非零奇異值的逆)最后把它們映射回正確的奇異向量(`V`的列),很簡單,是吧?
這實際上是計算`a`的偽逆的過程,它利用了一個標準正交基的一個關鍵性質:轉置就是逆。這就是 SVD 如此強大的原因。(在實踐中,真正的線性系統求解器不使用 SVD,因為它們計算是相當昂貴。還有其他更便宜的方法來分解矩陣,比如 QR、LU 或喬列斯基分解)。
然而,我們在匆忙中漏掉了一個小細節。如果奇異值為零會怎樣?我們不能取零為倒數,因為`1/0=∞`。這就是為什么它叫偽逆。(矩形矩陣沒有真實逆的定義,只有方陣(只要所有特征值非零)。無論輸入什么,它的奇異值都為零;沒有辦法重新跟蹤它的步驟并得出原始的輸入。
好吧,讓我們倒回來看這個小細節。讓我們帶著我們學到的,再往前走看看能不能把機器拆開。假設我們得到了`Aw=y`的答案,我們稱它為特定的`w`,因為它特別適合`y`。假設還有一堆輸入向量`A`被壓到 0。讓我們選一個,稱它為 Wsad-trumpet。因為wah。那么當我們把 Wparticular 添加到 Wsad-trumpet,您認為會發生什么呢?
```
A(Wparticular + Wsad-trumpet) = y
```
神奇!這也是一個解。事實上,任何被壓縮到零的輸入都可以被添加到一個特定的解中,并解決方案是這樣的:
```
Wgeneral = Wparticular + Whomogeneous
```
Wparticular 是方程`Aw=y`的精確解,可能有也可能沒有這樣的解。如果沒有,那么系統只能近似地解決。如果有,那么`y`屬于已知的`a`的列空間,列空間是`A`可以映射到的向量集合,通過它的列的線性組合。
Whomogeneous 是方程`Aw = 0`的解。(Wsadd-trumpet 的完整名稱是“Whomogeneous”。)這一點現在應該很熟悉了。所有的廣義向量的集合構成了`a`的零空間,這是具有奇異值為 0 的右奇異向量張成的空間。
“零空間”這個名字聽起來像是一場生死攸關的危機的結局。如果零空間包含除零向量之外的任何向量,那么就有方程`Aw = y`有無窮多個解,有太多的解可供選擇
來自本身并不是一件壞事。有時任何解決方案都可以。
但是如果有許多可能的答案,那么就有許多對分類任務有用的特性集。很難理解哪些是真正重要的。
解決大零空間問題的一種方法是通過添加來調節模型
額外的約束:
Aw = y,其中ww = c
這種正則化形式使得權向量具有一定的范數。這種正則化的強度是由正則化參數控制的,正則化參數必須進行調整,就像我們在實驗中所做的那樣。
一般來說,特性選擇方法處理選擇最有用的特性來減少計算負擔,減少模型的混亂程度,并使學習的模式更獨特。這是“特性選擇”的重點。
另一個問題是數據矩陣的“不均勻性”。當我們訓練一個線性分類器時,我們不僅關心線性系統有一個通解,而且關心我們能輕易地找到它。通常,訓練過程使用一個求解器,它通過計算損失函數的梯度和以小步驟下坡來工作。當某些奇異值非常大,而另一些非常接近于零時,求解者需要仔細地遍歷較長的奇異向量(那些對應于較大奇異值的向量),并花費大量時間挖掘較短的奇異向量以找到真正的答案。在光譜中這種“不均勻性”是由矩陣的條件數來衡量的,它基本上是最大和最小絕對值之間的比值。
綜上所述,為了有一個相對獨特的好的線性模型,為了讓它容易被發現,我們希望:
1、標簽向量可以通過特征子集(列向量)的線性組合很好地逼近。更好的是,特性集應該是線性無關的。
2、為了使零空間很小,行空間必須很大。(這是因為這兩個子空間是正交的。)數據點(行向量)的集合越線性無關,零空間就越小。
?為了便于求解,數據矩陣的條件數——最大奇異值與最小奇異值之比——應該很小。
## 分類器的概述
使用統計分類或分類器的方法來識別一個或者一組新的觀察將屬于哪個類別。書中引用的大多數方法都屬于監督學習領域,在監督學習中,分類是通過使用預先確定的類別標記的訓練數據進行算法確定的。我們將在這里給出這些算法的高級視圖,僅僅足以理解它們在文本中的應用。(實際上,維基百科是你最好的朋友,因為它在每一種方法中都能找到很好的參考文獻。)
### 支持向量機的徑向基函數核
支持向量機徑向基函數核(RBF SVM)
在Scikit Learn的sklearn.gaussian_process.kernes.RBF包
### K-最近鄰
K-最近鄰(kNN)
Scikit Learn的sklearn-neighbors包
### 隨機森林
隨機森林(RF)
隨機森林分類器在Scikit Learn的sklearn.ensembles包中
### 梯度提升樹
梯度提升樹(GBT)
梯度提升樹分類器在Scikit Learn的 sklearn.ensembles包中
嚴格地說,這里給出的公式是線性回歸,而不是線性分類。不同的是,回歸允許實值目標變量,而分類目標通常是表示不同類的整數。一個回歸子可以通過非線性的變換轉化為一個分類器。例如,logistic回歸分類器通過logistic函數傳遞輸入的線性變換。這些模型被稱為廣義線性模型,其核心是線性函數。雖然這個例子是關于分類的,但是我們使用線性回歸公式作為教學工具,因為它更容易分析。直覺容易映射到廣義線性分類器
實際上,它比那要復雜一些。$y$可能不在它的列空間中,所以這個方程可能沒有解。統計機器學習不是放棄,而是尋找一個近似的解決方案。它定義了一個量化解決方案質量的損失函數。如果解是精確的,那么損失是0。小錯誤,小損失;大錯誤,大損失等等。然后,訓練過程尋找最佳參數來最小化這個損失函數。在普通線性回歸中,損失函數稱為平方剩余損失,它本質上是將$y$映射到列空間中$A$的最近點。邏輯回歸最小化了日志丟失。在這兩種情況下,以及一般的線性模型中,線性系統$Aw = y$通常位于核心。因此,我們的分析是非常相關的。
