# 六、降維:用 PCA 壓縮數據集
> 譯者:[@cn-Wziv](https://github.com/cn-Wziv)
>
> 校對者:[@HeYun](https://github.com/KyrieHee)
通過自動數據收集和特征生成技術,可以快速獲得大量特征,但并非所有這些都有用。在[第 3 章](https://www.safaribooksonline.com/library/view/feature-engineering-for/9781491953235/ch03.html#chap-basic-text)和
在[第 4 章](https://www.safaribooksonline.com/library/view/feature-engineering-for/9781491953235/ch04.html#chap-tfidf)中,我們討論了基于頻率的濾波和特征縮放修剪無信息的特征。現在我們來仔細討論一下使用*主成分分析*(PCA)進行數據降維。
本章標志著進入基于模型的特征工程技術。在這之前,大多數技術可以在不參考數據的情況下定義。對于實例中,基于頻率的過濾可能會說“刪除所有小于`n`的計數“,這個程序可以在沒有進一步輸入的情況下進行數據本身。 另一方面,基于模型的技術則需要來自數據的信息。例如,PCA 是圍繞數據的主軸定義的。 在之前的技術中,數據,功能和模型之間從來沒有明確的界限。從這一點前進,差異變得越來越模糊。這正是目前關于特征學習研究的興奮之處。
## 引言
降維是關于擺脫“無信息的信息”的同時保留關鍵點。有很多方法可以定義“無信息”。PCA 側重于線性依賴的概念。在“[矩陣的剖析](https://www.safaribooksonline.com/library/view/feature-engineering-for/9781491953235/app01.html#sec-basic-linalg)”中,我們將數據矩陣的列空間描述為所有特征向量的跨度。如果列空間與特征的總數相比較小,則大多數特征是幾個關鍵特征的線性組合。如果在下一步管道是一個線性模型,然后線性相關的特征會浪費空間和計算能力。為了避免這種情況,主成分分析嘗試去通過將數據壓縮成更低維的線性來減少這種“絨毛”子空間。
在特征空間中繪制一組數據點。每個數據點都是一個點,整個數據點集合形成一個 blob。在[圖 6-1(a) ](https://www.safaribooksonline.com/library/view/feature-engineering-for/9781491953235/ch06.html#fig-data-blobs)中,數據點在兩個特征維度上均勻分布,blob 填充空間。在這個示例中,列空間具有完整的等級。但是,如果其中一些特征是其他特征的線性組合,那么該 blob 看起來不會那么豐滿; 它看起來更像[圖 6-1(b)](https://www.safaribooksonline.com/library/view/feature-engineering-for/9781491953235/ch06.html#fig-data-blobs),這是一個平面斑點,其中特征 1 是特征 2 的重復(或標量倍數)。在這種情況下,我們說該 blob 的本征維數是 1,即使它位于二維空間之中。
在實踐中,事情很少完全相同。這更可能是我們看到非常接近平等但不完全相同的特征。在這種情況下,數據 blob 可能如[圖 6-1(c) ](https://www.safaribooksonline.com/library/view/feature-engineering-for/9781491953235/ch06.html#fig-data-blobs)所示。這是一個憔悴的一團。要是我們想要減少傳遞給模型的特征的數量,那么我們可以用一個新特征替換特征 1 和特征 2,可能稱之為位于兩個特征之間的對線的 1.5 特征。原始數據集可以是用一個數字充分表示——沿著特征方 1.5 的方向——而不是兩個維度`f1`和`f2`。
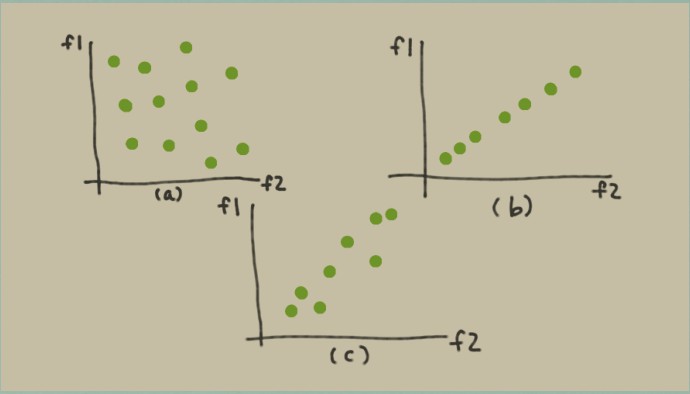
**圖 6-1 特征空間中的數據 blobs(a) 滿秩數據 blob(b) 低維數據 blob(c) 近似低維的數據 blob**
這里的關鍵思想是**用一些充分總結原始特征空間中包含的信息的新特征取代冗余特征**。當只有兩個特征的時候新特征很容易得到。這在當原始特征空間具有數百或數千個維度時將變得很難。我們需要一種數學描述我們正在尋找的新功能的方法。這樣我們就可以使用優化技術來找到它們。
數學上定義“充分總結信息”的一種方法要求就是這樣說新數據 blob 應該保留盡可能多的原來的列。我們是將數據塊壓扁成平坦的數據餅,但我們希望數據餅盡可能在正確的方向上。這意味著我們需要一種衡量特征列的方法。特征列與距離有關。但是在一些數據點中距離的概念有些模糊。可以測量任意兩對之間的最大距離點。但事實證明,這是一個非常困難的數學優化功能。另一種方法是測量任意一對點之間的平均距離,或者等價地,每個點與它們的平均值之間的平均距離,即方差。事實證明,這優化起來要容易得多。(生活很難,統計學家已經學會了采取簡便方法)在數學上,這體現為最大化新特征空間中數據點的方差。
## 導航線性代數公式的提示
為了保持面向線性代數的世界,保持跟蹤哪些數量標量,它們是向量,向量的方向是垂直還是水平。知道你的矩陣的維度,因為他們經常告訴你感興趣的向量是否在行或列中。繪制矩陣和向量作為頁面上的矩形,并確保形狀匹配。就像通過記錄測量單位(距離以英里,速度以英里/小時計)一樣,在代數中可以得到很大的代數,在線性代數中,所有人都需要的是尺寸。
## 求導
#
# 提示和符號
如前所述,讓`X`表示`n×d`數據矩陣,其中`n`是數據點的數量`d`是特征的數量。令`X`是包含單個數據點的列向量(所以`x`是`X`中其中一行的轉置)。設`W`表示我們試圖找到的新的特征向量或主要分量之一。
### 矩陣的奇異值分解(SVD)
任何矩形矩陣都可以分解為三個特定形狀和特征的矩陣:

這里, 和 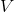 是正交矩陣(即  并且 ,
 是對角線包含`X`的奇異值的矩陣,它可以是正的,零的或負的。
假設  有`n`行`d`列且`n≥d`,那么  的大小為`n x d`, 和 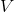 的大小為`d x d`。(請參閱[“奇異值分解(SVD)”](https://www.safaribooksonline.com/library/view/feature-engineering-for/9781491953235/app01.html#sec-svd)來獲得矩陣的 SVD 和特征分解的完整評論。)
公式 6-1 有用的平方和標識

## 線性投影
讓我們逐步分解 PCA 的推導。PCA 使用線性投影將數據轉換為新的特征空間。 [圖 6-2(c)](https://www.safaribooksonline.com/library/view/feature-engineering-for/9781491953235/ch06.html#fig-pca)說明了線性投影是什么樣子。當我們將  投影到 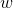 時,投影的長度與兩者之間的內積成正比,用`w`(它與它本身的內積)進行規范歸一化。稍后,我們將`w`單位化。所以只有相關部分是分子。
公式 6-2 投影坐標

請注意,`z`是一個標量,而  和  是列向量。由于有一堆的數據點,我們可以制定所有投影坐標的向量在新特征 。這里, 是熟悉的數據矩陣,其中每行是數據點,得到的  是一個列向量。
公式6-4 投影坐標向量

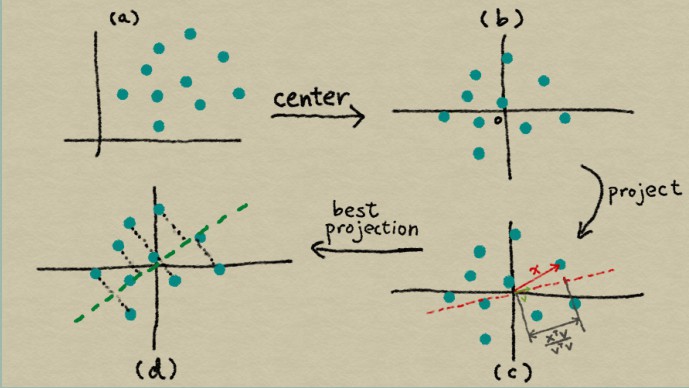
圖 6-2 PCA 的插圖
(a)特征空間中的原始數據,(b)以數據為中心 (c)將數據向量`x`投影到另一向量`v`上,(d)使投影坐標的方差最大化的方向是  的主要特征向量。
## 方差和經驗方差
下一步是計算投影的方差。方差定義為到均值的距離的平方的期望。
公式 6-6 隨機變量`Z`的方差
![Var(Z)=E[Z-E(Z)]^2](https://img.kancloud.cn/86/7e/867e4b0a043b8fa335215aadce870084_192x21.gif)
有一個小問題:我們提出的問題沒有提到平均值 ;它是一個自由變量。一個解決方案是從公式中刪除它,從每個數據點中減去平均值。結果數據集的平均值為零,這意味著方差僅僅是  幾何的期望值,減去平均值會產生數據居中效應。 (見[圖 6-2](https://www.safaribooksonline.com/library/view/feature-engineering-for/9781491953235/ch06.html#fig-pca)(`a-b`))。密切相關的量是兩個隨機變量`Z1`和`Z2`之間的協方差。把它看作是方差思想的擴展(單個隨機變量)到兩個隨機變量。
公式 6-8 兩個隨機變量`Z1`和`Z2`之間的協方差
![Cov(Z_1,Z_2)=E[(Z_1-E(Z_1))(Z_2-E(Z_2))]](https://img.kancloud.cn/7a/e6/7ae66429c66936e8d09c035914a3f7fa_346x19.gif)
當隨機變量的均值為零時,它們的協方差與它們的線性相一致相關性 ![E[Z_1,Z_2]](https://img.kancloud.cn/45/45/4545cce7a9fb015e1a0ca045f0489dbe_69x18.gif)。 稍后我們會聽到更多關于這個概念的信息。
數據上定義了統計量,如方差和期望值分配。 在實踐中,我們沒有真正的分布,但只有一堆觀察數據點`z1, ..., z n`。這被稱為經驗分布,它給我們一個方差的經驗估計。
公式 6-10 基于觀察`z`得到`Z`的經驗方差
## 公式法:第一個要素
結合[公式 6-2](https://www.safaribooksonline.com/library/view/feature-engineering-for/9781491953235/ch06.html#projection-coordinate)中  的定義,我們有以下公式用于最大化投影數據的方差。(我們從中刪除分母`n-1`經驗方差的定義,因為它是一個全局常數而不是影響價值最大化的地方。)
公式 6-12 主成分的目標函數
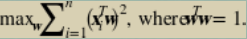
這里的約束迫使 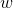 與其自身的內積為 1,這是相當于說向量必須有單位長度。這是因為我們只關心 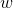 的方向而不是 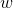 的大小。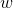 的大小是 1 不必要的自由度,所以我們把它設置為任意的值。
## 主要成分:矩陣-向量表達式
接下來是棘手的一步。[公式 6-12](https://www.safaribooksonline.com/library/view/feature-engineering-for/9781491953235/ch06.html#pca1)中的平方和是相當的繁瑣。它在矩陣向量格式中會更清晰。我們能做到嗎?答案是肯定的。關鍵在于平方和的同一性:一組平方項的和等于向量的平方范數,其元素是那些項,這相當于向量的內積。有了這個標識,我們可以用矩陣向量表示法重寫[公式 6-12](https://www.safaribooksonline.com/library/view/feature-engineering-for/9781491953235/ch06.html#pca1)。
6-4 主成分的目標函數,矩陣-向量表達式

PCA 的這種表述更明確地提出了目標:我們尋找一個輸入最大化輸出的標準的方向。這聽起來很熟悉嗎? 答案在于`X`的奇異值分解(SVD)。最優 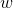 是  的主要左奇異向量,它也是  的主特征向量。投影數據被稱為原始數據的主成分。
## 主成分的一般解決方案
這個過程可以重復。一旦找到第一個主成分,我們就可以重新運行[公式 6-14](https://translate.google.cn/#en/zh-CN/This%20process%20can%20be%20repeated.%20Once%20we%20find%20the%20first%20principal%20component%2C%20we%20can%0Arerun%20Equation%206-14%20with%20the%20added%20constraint%20that%20the%20new%20vector%20be%20orthogonal%20to%0Athe%20previously%20found%20vectors),并添加新向量與之正交的約束條件先前發現的向量.
公式 6-16 目標函數的`k + 1`個主成分
, where \, 
該解是`X`的第`k+1`個左奇異向量,按奇異值降序排序。因此,前`k`個主成分對應于前`k`個`X`的左奇異向量。
## 轉換功能
一旦找到主成分,我們可以使用線性轉換特征投影。令  是`X`和`S`的 SVD,第`k`列中包含的矩陣前`k`個左奇異向量。`X`的維數為`nxd`,其中`d`是個數原始特征,并且  具有尺寸`d×k`。 而不是單個投影如[公式 6-4 ](https://www.safaribooksonline.com/library/view/feature-engineering-for/9781491953235/ch06.html#projection-vector)中的向量,我們可以同時投影到`a`中的多個向量投影矩陣。
公式 6-18 PCA 投影矩陣

投影坐標矩陣易于計算,并且可以使用奇異向量彼此正交的事實來進一步簡化。
公式 6-19 簡單的 PCA 轉換
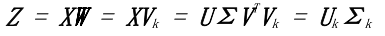
投影值僅僅是第一個按比例縮放的前k個右向奇異向量`k`個奇異值。因此,整個 PCA 解決方案,成分和投影可以通過`X`的 SVD 方便地獲得。
## 實現 PCA
PCA 的許多推導涉及首先集中數據,然后采取特征協方差矩陣的分解。但實現 PCA 的最簡單方法是通對中心數據矩陣進行奇異值分解。
### PCA 實現步驟
公式 6-20 數據矩陣中心化
,其中`1`是全部是 1 的列向量,并且`μ`是包含`X`的平均行數的列向量。
公式 6-21 計算 SVD

公式 6-22 主成分
前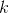個主分量是 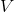 的前`k`列,即右奇異向量對應于`k`個最大奇異值。
公式 6-23 轉換數據
轉換后的數據只是`U`的前`k`列。(如果需要 whitening,然后通過逆奇異值對向量進行縮放。這需要選擇奇異值不為零。參見[“whitening 和 ZCA”](https://www.safaribooksonline.com/library/view/feature-engineering-for/9781491953235/ch06.html#sec-whitening))
## PCA 執行
讓我們更好地了解 PCA 如何將其應用于某些圖像數據。[MNIST](http://yann.lecun.com/exdb/mnist/) 數據集包含從 0 到 9 的手寫數字的圖像。原始圖像是`28 x 28`像素。使用 scikit-learn 分發圖像的較低分辨率子集,其中每個圖像被下采樣為`8×8`像素。原始數據在 scikit 學習有 64 個維度。我們應用 PCA 并使用第一個可視化數據集三個主要部分。
示例 6-1 scikit-learn 數字數據集(MNIST 數據集的一個子集)的主成分分析。
```py
>>> from sklearn import datasets
>>> from sklearn.decomposition import PCA
# Load the data
>>> digits_data = datasets.load_digits()
>>> n = len(digits_data.images)
# Each image is represented as an 8-by-8 array.
# Flatten this array as input to PCA.
>>> image_data = digits_data.images.reshape((n, -1))
>>> image_data.shape(1797, 64)
# Groundtruth label of the number appearing in each image
>>> labels = digits_data.target
>>> labels
array([0, 1, 2, ..., 8, 9, 8])
# Fit a PCA transformer to the dataset.
# The number of components is automatically chosen to account for
# at least 80% of the total variance.
>>> pca_transformer = PCA(n_components=0.8)
>>> pca_images = pca_transformer.fit_transform(image_data)
>>> pca_transformer.explained_variance_ratio_
array([ 0.14890594, 0.13618771, 0.11794594, 0.08409979, 0.05782415,
0.0491691 , 0.04315987, 0.03661373, 0.03353248, 0.03078806
,
0.02372341, 0.02272697, 0.01821863])
>>> pca_transformer.explained_variance_ratio_[:3].sum()
0.40303958587675121
# Visualize the results
>>> import matplotlib.pyplot as plt
>>> from mpl_toolkits.mplot3d import Axes3D
>>> %matplotlib notebook
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111, projection='3d')
>>> for i in range(100):
... ax.scatter(pca_images[i,0], pca_images[i,1], pca_images[i,2],
... marker=r''.format(labels[i]), s=64)
>>> ax.set_xlabel('Principal component 1')
>>> ax.set_ylabel('Principal component 2')
>>> ax.set_zlabel('Principal component 3')
```
前 6 個投影圖像的圖片顯示在[圖 6-3 ](http://https://www.safaribooksonline.com/library/view/feature-engineering-for/9781491953235/ch06.html#fig-mnist-pca)的 3D 圖中。標記對應于標簽。前三個主成分大約占數據集總差的 40%。這絕不是完美的,但它允許方便的低維可視化。我們看到 PCA 組類似數字彼此接近。數字 0 和 6 位于同一區域,如同 1 和 17,3 和 9。該空間大致分為 0,4 和 6 一側,其余數字是其他類的。

圖 6-3 PCA 預測 MNIST 數據的子集。標記對應于圖像標簽。
由于數字之間有相當多的重疊,因此很難清楚的將它們在投影空間中使用線性分類器分開。因此,如果任務是分類手寫數字并且選擇的模型是一個線性分類器,前三個主成分不足以作為功能。盡管如此有趣的是只有 3 個可以捕獲多少個 64 維數據集尺寸。
## 白化和 ZCA
由于目標函數中的正交性約束,PCA 變換產生了很好的附帶作用:轉換后的特征不再相關。再換句話說,特征向量對之間的內積是零。這很容易使用奇異向量的正交性來證明這一點:結果是包含奇異值的平方的對角矩陣表示每個特征向量與其自身的相關性,也稱為其 L2 規范。
有時候,將特征的比例標準化為1.在信號中是有用的處理方式,這就是所謂的*白化*。 它產生了一組與自身具有單位相關性,并且彼此之間的相關性為零的結果。在數學上,*白化*可以通過將 PCA 變換乘以反奇異值。
公式 6-24 PCA 白化
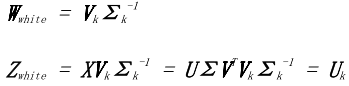
白化與維度降低無關;可以獨立執行不受其他的干擾。例如,零相分量分析(ZCA)(Bell 和 Sejnowski,1996)是一種與 PCA 密切相關的白化轉化,但事實并非減少特征的數量。ZCA 白化使用全套主要特征  沒有減少,并且包括一個額外的乘法回到 。
公式 6-25 ZCA 白化
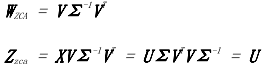
簡單的 PCA 投影([公式 6-19](https://www.safaribooksonline.com/library/view/feature-engineering-for/9781491953235/ch06.html#pca-projection))在新特征中產生坐標空間,主成分作為基礎。這些坐標表示只有投影向量的長度,而不是方向。乘以主成分給我們的長度和方向。另一個有效解釋是,多余的乘法將坐標旋轉回原點原始特征空間。(`V`是正交矩陣,并且正交矩陣旋轉他們的輸入不拉伸或壓縮)。所以 ZCA 白化產生的數據盡可能接近原始數據(歐幾里德距離)。
## 主成分分析的局限性
當使用 PCA 進行降維時,必須解決使用多少個主成分(`k`)的問題。像所有的超參數一樣,這個數字可以根據最終模型的質量進行調整。但也有啟發式算法不涉及高度的計算方法。
一種可能性是選擇`k`來解釋總方差的所需比例。(該選項在 scikit-learn 軟件包的 PCA 中可用)投影到第k個分量上:=,這是正方形  的第`k`個最大奇異值。`a`的奇異值的有序列表矩陣被稱為其頻譜。因此,為了確定要使用多少個成分,人們可以對數據矩陣進行簡單的頻譜分析并選擇閾值保留足夠的差異。
## 基于占用方差的k選擇
要保留足夠的成分覆蓋數據總方差的80%,請這樣選擇`k`:。
另一種選擇k的方法涉及數據集的固有維度。這個是一個更朦朧的概念,但也可以從頻譜中確定。基本上,如果譜包含一些很大的奇異值和一些小奇異值,那么可能只是收獲最大的奇異值并丟棄其余的值。有時候其余的頻譜不是很小,但頭部和尾部值之間有很大差距。這也是一個合理的截止點。 該方法需要光譜進行視覺檢查,因此不能作為自動化管線的一部分執行。
對 PCA 的一個關鍵批評是轉變相當復雜,并且結果因此很難解釋。主成分和投影向量是真實的價值,可能是積極的或消極的。主成分是(居中)行的基本線性組合,以及投影值為列的線性組合。例如,在股票申報中,每個因素都是股票收益時間片的線性組合。那是什么意思?學習因素很難附加人為的理解原因。因此,分析師很難相信結果。如果你不能解釋你為什么正在把數十億其他人的錢放在特定的股票上,你可能會這樣做將不會選擇使用該模型。
PCA 在計算上是繁雜的的。它依賴于 SVD,這是一個昂貴的過程。計算一個矩陣的全 SVD 需要  操作 [Golub 和 Van Loan,2012],假設`n≥d`,即數據點比特征更多。即使我們只需要`k`個主成分,計算截斷 SVD(`k`個最大奇異值和向量)仍然需要 操作。這是令人望而生畏的當有大量數據點或特征時。
以流媒體方式,批量更新或者從 PCA 執行 PCA是 很困難的完整數據的樣本。SVD 的流式計算,更新 SVD 和從一個子樣本計算 SVD 都是很難研究的問題。算法存在,但代價是精度降低。一個含義是人們應該期待將測試數據投影到主成分上時代表性較低在訓練集上找到。隨著數據分布的變化,人們不得不這樣做重新計算當前數據集中的主成分。
最后,最好不要將 PCA 應用于原始計數(字數,音樂播放次數,電影觀看次數等)。這是因為這種計數通常包含在內大的異常值。(這個概率非常高,有粉絲觀看了 314,582 次“指環王”,這讓其余的人望而生畏計數)。正如我們所知,PCA 在特征中查找線性相關性。相關性和方差統計對大的異常值非常敏感; 單一大量的數據可能會改變很多。 所以,首先修剪是個好主意大數值的數據(“[基于頻率的濾波](https://www.safaribooksonline.com/library/view/feature-engineering-for/9781491953235/ch03.html#sec-freq-filter)”)或應用縮放變換如 tf-idf([第 4 章](https://www.safaribooksonline.com/library/view/feature-engineering-for/9781491953235/ch04.html#chap-tfidf))或日志轉換(“[日志轉換](https://www.safaribooksonline.com/library/view/feature-engineering-for/9781491953235/ch02.html#sec-log-transform)”)。
## 用例
PCA 通過查找線性相關模式來減少特征空間維度功能之間。由于涉及 SVD,PCA 計算數千個功能的代價很高。但是對于少量的實值特征而言,它非常重要值得嘗試。
PCA 轉換會丟棄數據中的信息。因此,下游模型可能會訓練成本更低,但可能不太準確。在 MNIST 數據集上,有一些觀察到使用來自 PCA 的降維數據導致不太準確分類模型。在這些情況下,使用 PCA 有好處和壞處。
PCA 最酷的應用之一是時間序列的異常檢測。Lakhina,Crovella 和 Diot [2004] 使用 PCA 來檢測和診斷異常互聯網流量。他們專注于數量異常情況,即當出現波動或波動時減少從一個網絡區域到另一個網絡區域的通信量。這些突然更改可能表示配置錯誤的網絡或協調的拒絕服務攻擊。無論哪種方式,知道何時何地發生這種變化對互聯網都是有價值的運營商。
由于互聯網上的交通總量非常之多,孤立的激增規模很小地區很難被發現。一個相對較小的主干鏈路處理很多交通。 他們的重要見解是,數量異常會影響到多個鏈接同時(因為網絡數據包需要跳過多個節點才能到達他們的網絡目的地)。將每個鏈接視為一項功能,并將每個鏈接的流量數量對待時間步驟作為測量。數據點是流量測量的時間片跨越網絡上的所有鏈接。這個矩陣的主成分表明了網絡上的整體流量趨勢。其余的成分代表了剩余信號,其中包含異常。
PCA 也經常用于金融建模。在這些用例中,它作為一種類型工作因子分析,一組旨在描述觀察結果的統計方法使用少量未觀察因素的數據變異性。在因素分析中應用程序,目標是找到解釋性成分,而不是轉換數據。
像股票收益這樣的財務數量往往是相互關聯的。股票可以同時上下移動(正相關),也可以相反移動方向(負相關)。為了平衡波動和降低風險,投資組合需要多種不相關的股票其他。(如果籃子要下沉,不要把所有的雞蛋放在一個籃子里)尋找強大的相關模式有助于決定投資策略。
股票關聯模式可能在行業范圍內。 例如,科技股可能會上漲并一起下跌,而當油價高企時,航空股往往下跌。 但行業可能不是解釋結果的最好方式。 分析師也在尋找觀察到的統計數據中意外的相關性 特別是*文體因素模型* [Connor,1995] 在個體股票時間序列矩陣上運行 PCA 返回尋找共同變化的股票。 在這個用例中,最終目標是主成分本身,而不是轉換后的數據。
從圖像中學習時,ZCA 可作為預處理步驟。在自然的圖像中,相鄰像素通常具有相似的顏色。ZCA 白化可以消除這種相關性,這允許后續的建模工作集中在更有趣的圖像上結構。Alex Krizhevsky 的“[學習多層特征](http://www.cs.toronto.edu/~kriz/learning-features-2009-TR.pdf)”的論文圖像“包含很好的示例,說明 ZCA 影響自然圖片。
許多深度學習模型使用 PCA 或 ZCA 作為預處理步驟,但事實并非如此總是顯示是必要的。在“Factored 3-Way Restricted Boltzmann Machines forModeling Natural Images”中,Ranzato et al,評論,“白化不是必要的,但加快了算法的收斂速度。在“[An Analysis of Single-Layer Networks in Unsupervised Feature Learning](http://ai.stanford.edu/~ang/papers/aistats11-AnalysisSingleLayerUnsupervisedFeatureLearning.pdf)”中,Coates 等人 發現 ZCA 白化是有幫助的對于某些號,但不是全部。(請注意,本文中的模型是無監督功能學習模型。 所以 ZCA 被用作其他功能的特征方法工程方法。方法的堆疊和鏈接在機器中很常見學習管道。)
## 總結
這結束了對 PCA 的討論。關于 PCA 需要記住的兩件事是其機制(線性投影)和目標(最大化方差預計數據)。該解決方案涉及協方差的特征分解矩陣,它與數據矩陣的 SVD 密切相關。人們還可以記住 PCA 的精神圖像將數據擠壓成像蓬松一樣的煎餅可能。PCA 是模型驅動特征工程的一個示例。(應該立即懷疑當一個目標函數進入時,一個模型潛伏在背景中場景)。這里的建模假設是方差充分代表了包含在數據中的信息。等價地,該模型尋找線性特征之間的相關性。這在幾個應用程序中用于減少相關性或在輸入中找到共同因素。PCA 是一種眾所周知的降維方法。但它有其局限性作為高計算成本和無法解釋的結果。它作為一個預先定義好處理步驟,特別是在特征之間存在線性相關時。當被看作是一種消除線性相關的方法時,PCA 與其相關白化的概念。其表兄 ZCA 以可解釋的方式使數據變白,但是不會降低維度。
## 參考書目
Bell, Anthony J. and Terrence J. Sejnowski. 1996. “Edges are the ‘Independent
Components’ of Natural Scenes.” Proceedings of the Conference on Neural Information Processing Systems (NIPS) .
Coates, Adam, Andrew Y. Ng, and Honglak Lee. 2011. “An Analysis of Single-Layer
Networks in Unsupervised Feature Learning." International conference on artificial intelligence and statistics .
Connor, Gregory. 1995. “The Three Types of Factor Models: A Comparison of Their Explanatory Power." Financial Analysts Journal 51, no. 3: 42-46. http://www.jstor.org/stable/4479845.
Golub, Gene H., and Charles F. Van Loan. 2012. Matrix Computations . Baltimore and London: Johns Hopkins University Press; fourth edition.
Krizhevsky, Alex. 2009. “Learning Multiple Layers of Features from Tiny Images.”
MSc thesis, University of Toronto.
Lakhina, Anukool, Mark Crovella, and Christophe Diot. 2004. “Diagnosing network-wide traffic anomalies.” Proceedings of the 2004 conference on Applications, technologies,architectures, and protocols for computer communications (SIGCOMM ’04). DOI=http://dx.doi.org/10.1145/1015467.1015492
Ranzato, Marc’Aurelio, Alex Krizhevsky, and Geoffrey E. Hinton. 2010. “Factored 3-Way Restricted Boltzmann Machines for Modeling Natural Images." Proceedings of the 13-th International Conference on Artificial Intelligence and Statistics (AISTATS 2010)
