# 五、類別特征：機器雞時代的雞蛋計數 > 譯者：[@ZhenLeiXu](https://github.com/HadXu) 一個類別特征，見名思義，就是用來表達一種類別或標簽。比如，一個類別特征能夠表達世界上的主要城市，一年四季，或者說一個公司的產品(石油、路程、技術)。在真實世界的數據集中，類別值的數量總是無限的。同時這些值一般可以用數值來表示。但是，與其他數值變量不一樣的是，類別特征的數值變量無法與其他數值變量進行比較大小。(作為行業類型，石油與旅行無法進行比較)它們被稱之為非序的。 一個簡單的問題可以作為測試是否應該是一個分類變量的試金石測試：“兩個價值有多么不同，或者只是它們不同？”500美元的股票價格比100美元的價格高5倍。 所以股票價格應該用一個連續的數字變量表示。 另一方面，公司的產業（石油，旅游，技術等）應該無法被比較的，也就是類別特征。 大的分類變量在交易記錄中特別常見。 對于實例中，許多Web服務使用id作為分類變量來跟蹤用戶具有數百至數百萬的值，取決于唯一的數量服務的用戶。 互聯網交易的IP地址是另一個例子一個很大的分類變量。 它們是分類變量，因為即使用戶ID和IP地址是數字，它們的大小通常與任務無關在眼前。 例如，在進行欺詐檢測時，IP地址可能是相關的個人交易。 某些IP地址或子網可能會產生更多欺騙性交易比其他人。 但是164.203.x.x的子網本質上并不多欺詐性比164.202.x.x; 子網的數值無關緊要。 文檔語料庫的詞匯可以被解釋為一個大的分類變量，類別是唯一的單詞。 它可能在計算上很昂貴代表如此多的不同類別。 如果一個類別（例如，單詞）出現多個數據點（文檔）中的時間，然后我們可以將它表示為一個計數并表示所有的類別通過他們的統計數字。 這被稱為bin-counting。 我們用分類變量的共同表示開始討論，并且最終蜿蜒曲折地討論了大范圍的bin-counting問題變量，這在現代數據集中非常普遍。 ## 對類別特征進行編碼 分類變量的類別通常不是數字。例如，眼睛的顏色可以是“黑色”，“藍色”，“棕色”等。因此，需要使用編碼方法將這些非數字類別變為數字。 簡單地將一個整數（比如1到k）分配給k個可能的類別中的每一個都是誘人的。 但是，由此產生的價值觀可以互相授權，這在類別中不應該被允許。 ## One-hot 編碼 將類別特征進行表示一個最好的辦法就是使用一組比特位來表達。每一位代表一個可能的類別。 如果該變量不能一次成為多個類別，那么該組中只有一位可以是1。 這被稱為獨熱編碼，它在Scikit Learn中實現[sklearn.preprocessing.OneHotEncoder](http://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.OneHotEncoder.html)。 每個位都是一個特征。 因此是一個絕對的具有k個可能類別的變量被編碼為長度為k的特征向量。 表5-1 對3個城市的類別進行獨熱編碼 |City|e1|e2|e3| |:-:|:-:|:-:|:-:| |San Francisco|1|0|0| |New York|0|1|0| |Seattle|0|0|1| 獨熱編碼非常易于理解。 但它使用的是比嚴格必要的更多的一點。 如果我們看到k-1位是零，那么最后一位必須是1，因為變量必須具有k個值中的一個。 在數學上，可以寫下這個約束條件為“所有位的和必須等于1”。 等式 5-1. 獨熱編碼```e1,e2,e3```限制條件。 ```e1+e2+e3+...+ek=1``` 因此，我們有一個線性的依賴性。 線性相關特征，就像我們一樣在```tfidf```中發現，有點煩人，因為它意味著訓練線性模型不會是唯一的。 特征的不同線性組合可以做出同樣的預測，所以我們需要跳過額外條件的來理解特征對預測的影響。 ## dummy編碼 獨熱編碼的問題是它允許k個自由度，其中變量本身只需要k-1。 虛擬編碼通過僅使用表示中的k-1個特征來消除額外的自由度。 公共汽車下面有一個特征，由全零矢量表示。 這被稱為參考類別。 虛擬編碼和獨熱編碼都是在Pandas中以[pandas.get_dummies](http://pandas.pydata.org/pandas-docs/stable/generated/pandas.get_dummies.html)的形式實現的。 表5-2 對3個城市的類別進行dummy編碼 |City|e1|e2| |:-:|:-:|:-:| |San Francisco|1|0| |New York|0|1| |Seattle|0|0| 使用虛擬編碼進行建模的結果比單編碼更易解釋。這很容易在簡單的線性回歸問題中看到。 假設我們有一些數據關于三個城市的公寓租賃價格：舊金山，紐約和西雅圖。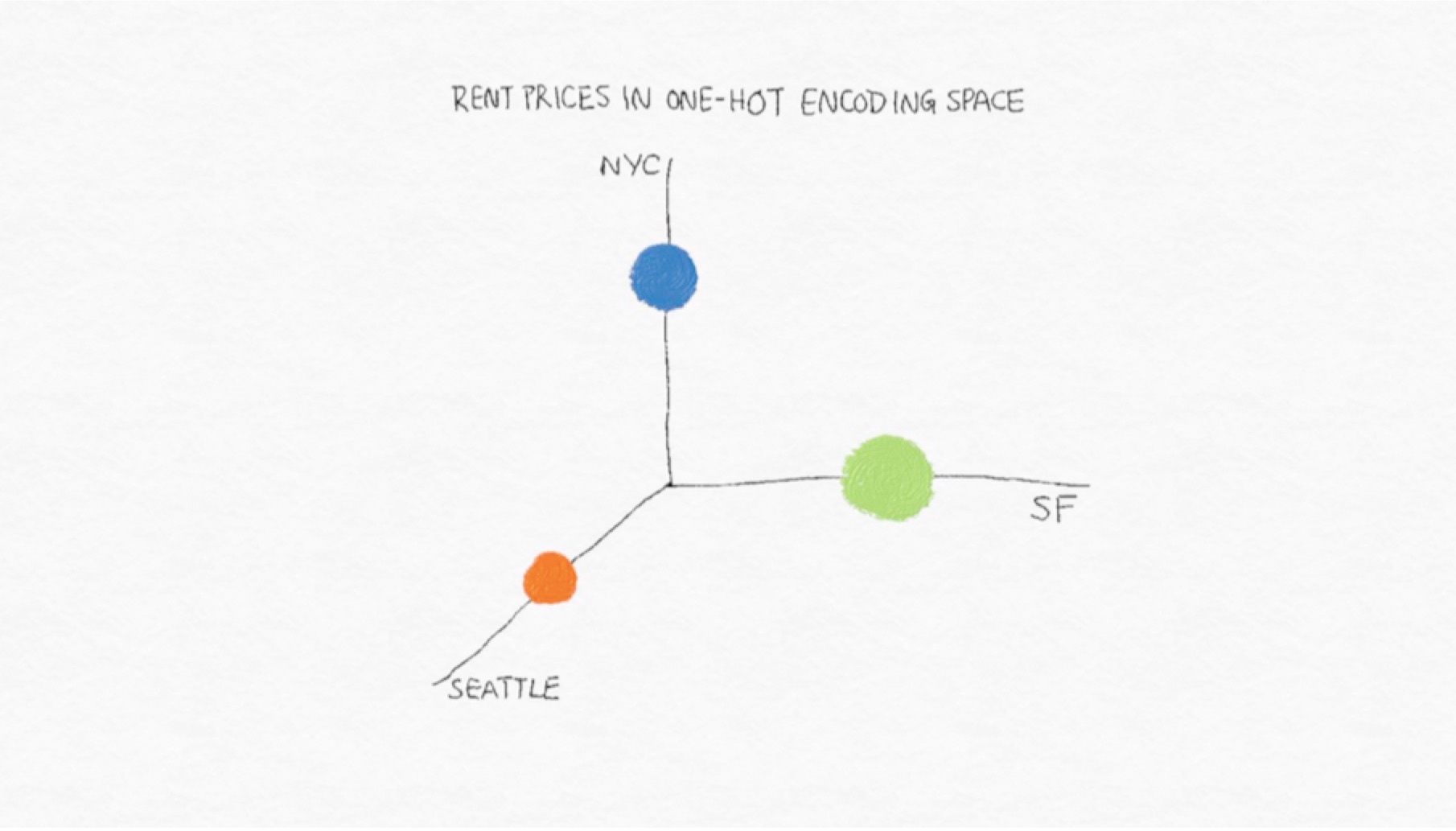（見表5-3） 表5-3 三個不同城市的公寓價格數據集 |id|city|Rent| |:-:|:-:|:-:| |0|SF|3999| |1|SF|4000| |2|SF|4001| |3|NYC|3499| |4|NYC|3500| |5|NYC|3501| |6|Seattle|2499| |7|Seattle|2500| |8|Seattle|2501|  圖5-1 公寓租金價格在one-hot編碼中的向量空間表示。點的大小表達了數據集中租金不同價格的平均數。 我們這時能夠僅僅依靠城市這一個變量來建立線性回歸來預測租金的價格。 線性回歸模型可以這樣寫 ```y=w1x1+w2x2+w3x3+...+wnxn``` 習慣上我們還添加一個常量來，這樣的話當x全部為0，y不會為0. 例5-1.在獨熱編碼上的線性回歸 ```python import pandas as pd from sklearn import linear_model df = pd.DataFrame({'City': ['SF', 'SF', 'SF', 'NYC', 'NYC', 'NYC','Seattle', 'Seattle', 'Seattle'], 'Rent': [3999, 4000, 4001, 3499, 3500, 3501, 2499,2500,2501]}) >>> df['Rent'].mean() 3333.3333333333335 one_hot_df = pd.get_dummies(df, prefix=['city']) >>> one_hot_df Rent city_NYC city_SF city_Seattle 0 3999 0 1 0 1 4000 0 1 0 2 4001 0 1 0 3 3499 1 0 0 4 3500 1 0 0 5 3501 1 0 0 6 2499 0 0 1 7 2500 0 0 1 8 2501 0 0 1 model = linear_model.LinearRegression() model.fit(one_hot_df[['city_NYC', 'city_SF', 'city_Seattle']], one_hot_df[['Rent']]) >>> model.coef_ array([[ 166.66666667, 666.66666667, -833.33333333]]) >>> model.intercept_ array([ 3333.33333333]) ``` 使用dummy code進行回歸 ```python dummy_df = pd.get_dummies(df, prefix=['city'], drop_first=True) >>> dummy_df Rent city_SF city_Seattle 0 3999 1 0 1 4000 1 0 2 4001 1 0 3 3499 0 0 4 3500 0 0 5 3501 0 0 6 2499 0 1 7 2500 0 1 8 2501 0 1 >>> model.fit(dummy_df[['city_SF', 'city_Seattle']], dummy_df['Rent']) LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False) >>> model.coef_ array([ 500., -1000.]) >>> model.intercept_ 3500.0 ``` 通過獨熱編碼，截距項表示目標變量的全局均值租金價格，并且每個線性系數表示該城市的平均租金與全局平均值的差異。 通過虛擬編碼，偏差系數代表響應的平均值參考類別的變量y，在這個例子中是紐約市。該第i個特征的系數等于平均響應之間的差異第i類別的值和參考類別的平均值。 表5-4：線性回歸學得的系數 |id|x1|x2|x3|b| |:-:|:-:|:-:|:-:|:-:| |one-hot|166.67|666.67|-833.33|3333.33| |dummy coding|0|500|-1000|3500| ## Effect編碼 分類變量編碼的另一種變體稱為Effect編碼。 Effect編碼與虛擬編碼非常相似，區別在于參考類別現在由所有-1的向量表示。 表5-5: Effect編碼表示3個城市 |City|e1|e2| |:-:|:-:|:-:| |San Francisco|1|0| |New York|0|1| |Seattle|-1|-1| Effect編碼與虛擬編碼非常相似，但是在線性回歸中更容易被擬合。例子5-2表達了運行機理。截距項表示目標的全球平均值變量，單個系數表示各個類別的平均值與全球平均值有多少差異。 （這被稱為類別或級別的主要效果，因此名稱為“效果編碼”。）獨熱編碼實際上具有相同的截距和系數，但在這種情況下，每個城市都有線性系數。 在效果編碼中，沒有單一特征代表參考類別。 因此，參考類別的影響需要分別計算為所有其他類別的系數的負和。(查看[what is effect coding?](https://stats.idre.ucla.edu)) 例子5-2 Effect編碼的線性回歸 ```python >>> effect_df = dummy_df.copy() >>> effect_df.ix[3:5, ['city_SF', 'city_Seattle']] = -1.0 >>> effect_df Rent city_SF city_Seattle 0 3999 1.0 0.0 1 4000 1.0 0.0 2 4001 1.0 0.0 3 3499 -1.0 -1.0 4 3500 -1.0 -1.0 5 3501 -1.0 -1.0 6 2499 0.0 1.0 7 2500 0.0 1.0 8 2501 0.0 1.0 >>> model.fit(effect_df[['city_SF', 'city_Seattle']], effect_df['Rent']) LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False) >>> model.coef_ array([ 666.66666667, -833.33333333]) >>> model.intercept_ 3333.3333333333335 ``` 類別變量的優點和缺點 獨熱，虛擬和效果編碼非常相似。 他們每個人都有優點和缺點。 獨熱編碼是多余的，它允許多個有效模型一樣的問題。 非唯一性有時候對解釋有問題。該優點是每個特征都明顯對應于一個類別。 此外，失蹤數據可以編碼為全零矢量，輸出應該是整體目標變量的平均值。 虛擬編碼和效果編碼不是多余的。 他們產生獨特和可解釋的模型。 虛擬編碼的缺點是它不能輕易處理缺少數據，因為全零矢量已經映射到參考類別。它還編碼每個類別相對于參考類別的影響，其中看起來很奇怪。 效果編碼通過使用不同的代碼來避免此問題參考類別。 但是，所有-1的矢量都是一個密集的矢量，對于存儲和計算來說都很昂貴。 因此，Pandas和Scikit Learn等流行的ML軟件包選擇了虛擬編碼或獨熱編碼，而不是效應編碼。當類別數量變得非常多時，所有三種編碼技術都會失效大。 需要不同的策略來處理非常大的分類變量。 ## 處理大量的類別特征 互聯網上的自動數據收集可以生成大量的分類變量。這在諸如定向廣告和欺詐檢測等應用中很常見。 在有針對性的廣告中，任務是根據用戶的搜索查詢或當前頁面將用戶與一組廣告進行匹配。 功能包括用戶ID，廣告的網站域，搜索查詢，當前頁面以及這些功能的所有可能的成對連詞。 （查詢是一個文本字符串，可以切分成常用的文本特征，但查詢通常很短，通常由短語組成，因此在這種情況下最好的行為通常是保持完整，或 通過哈希函數來簡化存儲和比較，我們將在下面更詳細地討論哈希。）其中每一個都是一個非常大的分類變量。 我們面臨的挑戰是如何找到一個能夠提高內存效率的優秀特征表示，并生成訓練速度快的準確模型。 對于這種類別特征處理的方案有： 1. 對編碼不做任何事情。 使用便宜的訓練簡單模型。 在許多機器上將獨熱編碼引入線性模型（邏輯回歸或線性支持向量機）。 2. 壓縮編碼，有兩種方式 a. 對特征進行哈希--在線性回歸中特別常見 b. bin-counting--在線性回歸中與樹模型都常見 使用one-hot編碼是可行的。在微軟搜索廣告研究中，Graepel等人 [2010]報告在貝葉斯概率回歸模型中使用這種二值特征，可以使用簡單更新在線進行培訓。 與此同時，其他組織則爭論壓縮方法。 來自雅虎的研究人員 通過特征散列發誓[Weinberger et al。2009年]。 盡管McMahan等人[2013]在谷歌的廣告引擎上嘗試了功能哈希，并沒有找到顯著的改進。 然而，微軟的其他人則被認為是計數[Bilenko，2015]。 我們將會看到，所有這些想法都有利有弊。 我們將首先描述解決方案本身，然后討論他們的權衡。 ## 特征哈希 散列函數是一個確定性函數，它映射一個潛在的無界整數到有限整數范圍[1，m]。 由于輸入域可能大于輸出范圍，多個數字可能會映射到相同的輸出。 這被稱為a碰撞。 統一的散列函數可確保大致相同數量的數字被映射到每個m箱。 在視覺上，我們可以將散列函數視為一臺機器可以吸入編號的球并將它們傳送到一個m箱。 球與相同的號碼將始終被路由到同一個bin。 散列函數可以為任何可以用數字表示的對象構造（對于可以存儲在計算機上的任何數據都是如此）：數字，字符串，復雜的結構等。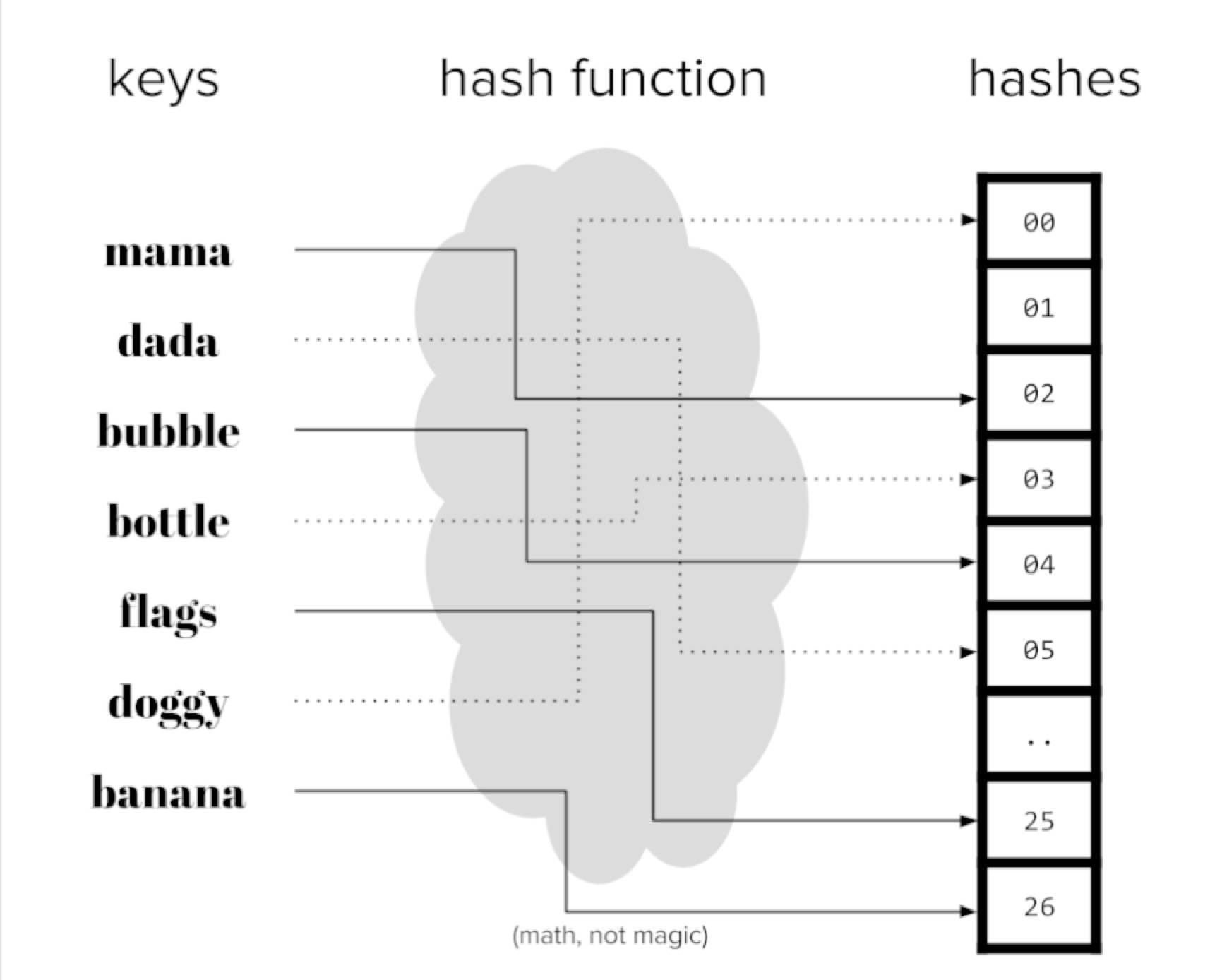  圖5-2 哈希編碼 當有很多特征時，存儲特征向量可能占用很多空間。 特征散列將原始特征向量壓縮為m維通過對特征ID應用散列函數來創建矢量。 例如，如果原件特征是文檔中的單詞，那么散列版本將具有固定的詞匯大小為m，無論輸入中有多少獨特詞匯。 例5-3 對單詞的特征哈希 ```python def hash_features(word_list,m): output = [0]*m for word in word_list: index = hash_fcn(word)%m output[index] += 1 return output ``` 功能散列的另一個變體添加了一個符號組件，因此計數也是從哈希箱中增加或減少。 這確保了內部產品之間散列特征與原始特征的期望值相同。 ```python def hash_features(word_list,m): output = [0]*m for word in word_list: index = hash_fcn(word)%m sign_bit = sign_hash(word) % 2 if(sign_bit==0): output[index] -= 1 else: output[index] += 1 return output ``` 哈希后內積的值在時間復雜度在```O(1/(m**0.5))```.所以哈希表m的大小可以根據可接受的錯誤來選擇。在實踐中，選擇合適的m可能需要一些試驗和錯誤。特征哈希可以用于涉及特征內積的模型矢量和系數，例如線性模型和核心方法。 它一直證明在垃圾郵件過濾任務中取得成功[Weinberger等，2009]。在有針對性的廣告案例中，McMahan et al。 [2013年]報告不能將預測誤差降低到可接受的水平，除非m的數量級為數十億。散列特征的一個缺點是散列特征是聚合的原始特征，不再可解釋。 在這個例子中，我們將使用Yelp評論數據集來演示存儲和,解釋性使用的為sklearn的庫```FeatureHasher```。在有針對性的廣告案例中，McMahan ```python import pandas as pd import json js = [] with open('yelp_academic_dataset_review.json') as f: for i in range(10000): js.append(json.loads(f.readline())) review_df = pd.DataFrame(js) m = len(review_df.business_id.unique()) >>>m 4174 In [4]: from sklearn.feature_extraction import FeatureHasher ...: ...: h = FeatureHasher(n_features=m, input_type='string') ...: ...: f = h.transform(review_df['business_id']) ...: In [5]: review_df['business_id'].unique().tolist()[0:5] Out[5]: ['9yKzy9PApeiPPOUJEtnvkg', 'ZRJwVLyzEJq1VAihDhYiow', '6oRAC4uyJCsJl1X0WZpVSA', '_1QQZuf4zZOyFCvXc0o6Vg', '6ozycU1RpktNG2-1BroVtw'] In [6]: f.toarray() Out[6]: array([[ 0., 0., 0., ..., 0., 0., 0.], [ 0., 0., 0., ..., 0., 0., 0.], [ 0., 0., 0., ..., 0., 0., 0.], ..., [ 0., 0., 0., ..., 0., 0., 0.], [ 0., 0., 0., ..., 0., 0., 0.], [ 0., 0., 0., ..., 0., 0., 0.]]) ``` 我們看看特征的存儲 ```python print('Our pandas Series, in bytes: ', getsizeof(review_df['business_id'])) print('Our hashed numpy array, in bytes: ', getsizeof(f)) >>>790104 >>>56 ``` 我們可以清楚地看到如何使用特征散列會以計算方式使我們受益，犧牲直接的用戶解釋能力。 這是一個容易的權衡來接受何時從數據探索和可視化發展到機器學習管道對于大型數據集。 ## bin-counting Bin-counting是機器學習中常見的重新發現之一。 從廣告點擊率預測到硬件分支預測，它已經被重新創建并用于各種應用[Yeh and Patt，1991; Lee等人，1998; Pavlov等，2009; 李等人，2010]。 然而，因為它是一種特征工程技術，而不是一種建模或優化方法，所以沒有關于該主題的研究論文。 關于該技術最詳細的描述可以在Misha Bilenko的博客文章“Big Learning Made with Easy”以及相關的幻燈片中找到。 bin-counting的想法非常簡單：而不是使用分類變量作為特征，而不是使用條件概率的目標在該價值下。 換句話說，而不是編碼的身份分類值，計算該值和該值之間的關聯統計量我們希望預測的目標。 對于那些熟悉Na?veBayes分類器的人來說，這個統計學應該敲響一下鐘，因為它是該類的條件概率假設所有功能都是獨立的。 最好用一個例。 表5-6. bin-counting的例子 |User|Number of clicks|Number of non-clicks|probability of click|QueryHash,AdDomain|Number of clicks|Number of non-clicks|probability of click| |:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:| |Alice|5|120|0.0400|0x598fd4fe,foo.com|5000|30000|0.167| |bob|20|230|0.0800|0x50fa3cc0,bar.org|100,900,0.100| |...| |joe|2|3|0.400|0x437a45e1,qux.net|6,18,0.250| Bin-counting假定歷史數據可用于計算統計。 表5-6包含分類變量每個可能值的匯總歷史計數。 根據用戶點擊任何廣告的次數以及未點擊的次數，我們可以計算用戶“Alice”點擊任何廣告的概率。 同樣，我們可以計算任何查詢 - 廣告 - 域組合的點擊概率。 在訓練時，每當我們看到“愛麗絲”時，都使用她的點擊概率作為模型的輸入特征。 QueryHash-AdDomain對也是如此，例如“0x437a45e1，qux.net”。 假設有10,000個用戶。 獨熱編碼會生成一個稀疏矢量長度為10,000，在列中對應于值的單個1當前數據點。 Bin-counting將所有10,000個二進制列編碼為一個功能的真實值介于0和1之間。 除了歷史點擊概率外，我們還可以包含其他功能：原始計數本身（點擊次數和非點擊次數），對數比率或任何其他概率的衍生物。 我們的例子是預測廣告點擊率，通過率。 但該技術很容易應用于一般的二元分類。 它也可以使用通常的技術容易地擴展到多級分類將二元分類器擴展到多個類，即通過一對多優勢比或其他多類標簽編碼。 ## Bin-counting的優勢比和對數比 比值比通常定義在兩個二元變量之間。 它通過提出這樣一個問題來看待他們的聯想強度：“當X為真時，Y有多大可能是真的”。例如，我們可能會問，“Alice點擊廣告的可能性大于 一般人口？“在這里，X是二進制變量”是Alice是當前用戶“，而Y是變量”點擊廣告與否“。 該計算使用所謂的雙向列聯表（基本上，四個數字對應于X和Y的四種可能組合）。 表5-7. 偶然發生的用戶點擊事件 ||click|Non-Click|Total| |:-:|:-:|:-:|:-:| |Alice|5|120|125| |Not Alice|995|18880|19875| |Total|1000|19000|20000| 給定輸入變量X和目標變量Y，優勢比定義為優勢比=(P(Y=1|X=1)/(P(Y=0|X=1))/(P(Y=1|X=0)/(P(Y=0|X=0)))) 在我們的例子中，這意味著“愛麗絲點擊廣告而不是點擊的可能性”和“其他人點擊而非點擊的可能性有多大”之間的比率。在這種情況下，數字是  更簡單地說，我們可以看看分子，它檢查多少可能性單個用戶（Alice）是否點擊廣告而不是點擊。 這適合大型具有許多值的分類變量，而不僅僅是兩個。  概率比率可能很容易變得非常小或非常大。 （例如，將會有幾乎不會點擊廣告的用戶，也可能是點擊廣告的用戶更頻繁得多）日志轉換再次來到我們的救援。 另一個對數的有用特性是它將一個劃分變為一個減法。  簡而言之，bin-counting將分類變量轉換為有關的統計信息值。 它變成了一個大的，稀疏的分類變量的二進制表示變成一個非常小，密集的實值數值表示。  圖5-3 分類變量的獨熱編碼與二進制計數統計的說明。 在實施方面，垃圾箱計數需要在每個類別之間存儲地圖及其相關計數。 （其余的統計數據可以從中得到原始計數）。因此它需要O（k）空間，其中k是唯一值的數量的分類變量。 我們采用Kaggle的比賽[Avazu](https://www.kaggle.com/c/avazu-ctr-prediction)舉個例子. #### Avazu Click數據集 * 有24個變量，包括'點擊'，一個二進制點擊/不點擊計數器和'device_id'，用于跟蹤顯示廣告的設備。 * 完整的數據集包含4,0428,967個觀測值，其中有2,686,408個獨特的設備。 Avazu競賽使用廣告數據來預測點擊率，但我們將使用它來演示如何bin計數可以大大減少大的特征空間流數據量。 例子5-6 Bin-counting例子 ```python import pandas as pd #讀取前面的10k行 df = pd.read_csv('data/train_subset.csv') #有多少獨立的特征 len(df['device_id'].unique()) #對于每一個類別，我們想計算 # Theta = [counts, p(click), p(no click), p(click)/p(no click)] def click_counting(x, bin_column): clicks = pd.Series(x[x['click'] > 0][bin_column].value_counts(), name='clicks') no_clicks = pd.Series(x[x['click'] < 1][bin_column].value_counts(), name='no_clicks') counts = pd.DataFrame([clicks,no_clicks]).T.fillna('0') counts['total_clicks'] = counts['clicks'].astype('int64') + counts['no_clicks'].astype('int64') return counts def bin_counting(counts): counts['N+'] = counts['clicks'].astype('int64').divide(counts['total_clicks'].astype('int64')) counts['N-'] = counts['no_clicks'].astype('int64').divide(counts['total_clicks'].astype('int64')) counts['log_N+'] = counts['N+'].divide(counts['N-']) bin_column = 'device_id' device_clicks = click_counting(df.filter(items= [bin_column, 'click']), bin_column) device_all, device_bin_counts = bin_counting(device_clicks) device_all.sort_values(by = 'total_clicks', ascending=False).head(4) clicks no_clicks total N+ N- log_N+ a99f214a 15729 71206 86935 0.180928 0.819072 0.220894 c357dbff 33 31da1bd0 0 936e92fb 5 134 167 62 62 54 59 0.197605 0.802395 0.246269 0.000000 1.000000 0.000000 0.084746 0.915254 0.092593 ``` ## 關于稀有類別 就像罕見的詞，罕見的類別需要特殊的處理。 想想一個用戶每年登錄一次：幾乎沒有數據可以可靠估計她廣告的點擊率。 而且，稀有類別會在計數表中浪費空間。解決這個問題的一種方法是通過補償，一種積累的簡單技術一個特殊垃圾箱中所有稀有類別的數量。 如果計數大于a一定的門檻，那么這個類別就有自己的統計數字。 否則，使用來自回退箱的統計數據。 這基本上會恢復單個的統計信息罕見類別與所有罕見類別的統計數據進行比較。 當使用back-off方法，它有助于為統計信息添加二進制指標來自后退箱。  圖5-4 如果罕見類別獲得收益，它可以使用自己的統計數據進行建模，從而超過回退庫的閾值。 還有另一種方法來處理這個問題，稱為count-min sketch [Cormode和Muthukrishnan，2005]。 在這種方法中，所有類別，罕見或頻繁類似通過多個散列函數進行映射，輸出范圍為m，遠小于類別的數量，k。 當檢索一個統計量時，計算所有的哈希值該類別，并返回最小的統計量。 擁有多個散列函數減輕單個散列函數內碰撞的可能性。 該計劃有效因為可以做出散列函數次數m，散列表大小小于k，類別的數量，仍然保持較低的整體碰撞可能性。  由于二進制計數依賴于歷史數據來生成必要的統計數據需要通過數據收集期等待，導致了數據收集時間的輕微延遲學習管道。 這也意味著當數據分布發生變化時，計數需要更新。 數據變化越快，計數需要的次數越多重新計算。 這對于目標應用程序尤其重要廣告，用戶偏好和熱門查詢變化非常快，而且缺乏適應當前的分布可能意味著廣告的巨大損失平臺。 有人可能會問，為什么不使用相同的數據集來計算相關統計量并訓練模型？這個想法看起來很無辜。這里最大的問題是統計涉及目標變量，這是模型試圖預測的。使用輸出來計算輸入特征會導致一個稱為泄漏的有害問題。簡而言之，泄漏意味著信息被揭示給模型，從而使它有更好的預測的不切實際的優勢。當測試數據泄露到訓練集中，或者未來的數據泄漏到過去時，可能會發生這種情況。任何時候都會向模型提供在生產中實時進行預測時應該無法訪問的信息，這會導致泄漏。 Kaggle的維基提供了更多泄漏示例以及為什么它對機器學習應用程序不利。 如果二進制計數程序使用當前數據點的標簽來計算輸入統計量的一部分，則這構成直接泄漏。防止這種情況的一種方法是在計數收集（用于計算箱計數統計）和訓練之間進行嚴格分離，即使用較早批次的數據點進行計數，將當前數據點用于訓練（將分類變量映射到歷史統計我們剛剛收集），并使用未來的數據點進行測試。這解決了泄漏問題，但引入了上述延遲（輸入統計信息，因此模型將跟蹤當前數據）。 事實證明，還有另一種基于差別隱私的解決方案。 如果統計數據的分布保持大致相同或不存在任何一個數據點，則該統計近似是防漏的。 在實踐中，增加一個分布拉普拉斯（0,1）的小隨機噪聲足以掩蓋單個數據點的任何潛在泄漏。 這個想法可以結合一次性計算來制定當前數據的統計數據。 Owen Zhang在他的“贏得數據科學競賽”的演講中詳細介紹了這個技巧。 ## Counts without bounds 如果在越來越多的歷史數據下統計數據不斷更新，原始數量將無限增長。這可能是模型的問題。訓練有素的模型“知道”輸入數據直至觀察到的比例。一個訓練有素的決策樹可能會說“當x大于3時，預測為1”。一個經過訓練的線性模型可能會說“乘以0.7的多個x并查看結果是否大于全局平均值”。這些可能是x介于0和5之間。但是除此之外會發生什么？沒有人知道。 當輸入計數增加時，模型將需要重新訓練以適應當前的比例。如果計數積累得相當緩慢，那么有效量表不會變得太快，并且模型不需要過于頻繁地重新訓練。但是當計數增加很快時，頻繁的再培訓將是一個麻煩。 出于這個原因，使用標準化計數通常會更好 以已知的時間間隔為界。例如，估計的點擊率是 有界[0，1]之間。另一種方法是采取對數變換，即施加一個 嚴格的限制，但是當數量非常大時，增加速度會很慢。 這兩種方法都不能防止轉移投入分布，例如，去年的芭比娃娃現在已經過時，人們將不再點擊這些廣告。該模型需要重新訓練以適應輸入數據分布中的這些更根本性的變化，否則整個流程將需要遷移到模型不斷適應輸入的在線學習環境。 ## 總結 #### Plain one-hot encoding 空間使用：O(n) 時間復雜度：O(nk) 優點: * 容易實現 * 更高的精度 * 在線學習特別容易擴展 缺點 * 計算不足 * 如果類別增加則不能夠使用 * 對線性模型以外的任何其他方法都不可行 * 對于大數據集需要分布式訓練 #### Feature hashing 空間使用：O(n) 時間復雜度：O(nm) 優點: * 容易實現 * 容易訓練 * 容易擴展到新類別 * 容易處理稀有類別 * 在線學習容易擴展 缺點 * 只能夠使用線性或核模型 * 哈希編碼很難解釋 * 精度有爭議 ## Bin-counting 空間使用：O(n+k) 時間復雜度：O(n) 優點: * 訓練快 * 能夠使用樹模型 * 容易擴展到新列類別 * 容易處理稀有類別 * 可解釋 缺點 * 需要利用歷史信息 * 對于在線學習有困難 * 會有數據泄露 正如我們所看到的，沒有任何方法是完美的。 選擇使用哪一個取決于所需的型號。 線性模型比較便宜，因此可以進行訓練處理非壓縮表示，例如獨熱編碼。 基于樹的模型，另一方面，需要反復搜索右側分割的所有特征，并且是因此限于小型表示，如箱計數。 功能哈希處于在這兩個極端之間，但是由此產生的精確度有不同的報道。