# 八、自動化特征提取器：圖像特征提取和深度學習 > 譯者：[@friedhelm739](https://github.com/friedhelm739) 視覺和聲音是人類固有的感覺輸入。我們的大腦是可以迅速進化我們的能力來處理視覺和聽覺信號的，一些系統甚至在出生前就對刺激做出反應。另一方面，語言技能是學習得來的。他們需要幾個月或幾年的時間來掌握。許多人天生就具有視力和聽力的天賦，但是我們所有人都必須有意訓練我們的大腦去理解和使用語言。 有趣的是，機器學習的情況是相反的。我們已經在文本分析應用方面取得了比圖像或音頻更多的進展。以搜索問題為例。人們在信息檢索和文本檢索方面已經取得了相當多年的成功，而圖像和音頻搜索仍在不斷完善。在過去五年中，深度學習模式的突破最終預示著期待已久的圖像和語音分析的革命。 進展的困難與從相應類型的數據中提取有意義特征的困難直接相關。機器學習模型需要語義上有意義的特征進行語義意義的預測。在文本分析中，特別是對于英語這樣的語言，其中一個基本的語義單位（一個詞）很容易提取，可以很快地取得進展。另一方面，圖像和音頻被記錄為數字像素或波形。圖像中的單個“原子”是像素。在音頻數據中，它是波形強度的單一測量。它們包含的語義信息遠少于數據文本。因此，在圖像和音頻上的特征提取和工程任務比文本更具挑戰性。 在過去的二十年中，計算機視覺研究已經集中在人工標定上，用于提取良好的圖像特征。在一段時間內，圖像特征提取器，如 SIFT 和 HOG 是標準步驟。深度學習研究的最新發展已經擴展了傳統機器學習模型的范圍，將自動特征提取作為基礎層。他們本質上取代手動定義的特征圖像提取器與手動定義的模型，自動學習和提取特征。人工標定仍然存在，只是進一步深入到建模中去。 在本章中，我們將從流行的圖像特征提取SIFT和HOG入手，深入研究本書所涵蓋的最復雜的建模機制：深度學習的特征工程。 ## 最簡單的圖像特征（為什么他們不好使） 從圖像中提取的哪些特征是正確的呢？答案當然取決于我們試圖用這些特征來做什么。假設我們的任務是圖像檢索：我們得到一張圖片并要求從圖像數據庫中得到相似的圖片。我們需要決定如何表示每個圖像，以及如何測量它們之間的差異。我們可以看看圖像中不同顏色的百分比嗎？圖8-1展示了兩幅具有大致相同顏色輪廓但有著非常不同含義的圖片；一個看起來像藍色天空中的白云，另一個是希臘國旗。因此，顏色信息可能不足以表征圖像。  另一個比較簡單的想法是測量圖像之間的像素值差異。首先，調整圖像的寬度和高度。每個圖像由像素值矩陣表示。矩陣可以通過一行或一列被堆疊成一個長向量。每個像素的顏色（例如，顏色的 RGB 編碼）現在是圖像的特征。最后，測量長像素向量之間的歐幾里得距離。這絕對可以區分希臘國旗和白云。但作為相似性度量，它過于嚴格。云可以呈現一千種不同的形狀，仍然是一朵云。它可以移動到圖像的一邊，或者一半可能位于陰影中。所有這些轉換都會增加歐幾里得距離，但是他們不應該改變圖片仍然是云的事實。 問題是單個像素不攜帶足夠的圖像語義信息。因此，使用它們用于分析結果是非常糟糕的。在 1999 年，計算機視覺研究者想出了一種更好的方法來使用圖像的統計數據來表示圖像。它叫做 Scale Invariant Feature Transform（SIFT）。 SIFT最初是為對象識別的任務而開發的，它不僅涉及將圖像正確地標記為包含對象，而且確定其在圖像中的位置。該過程包括在可能的尺度金字塔上分析圖像，檢測可以指示對象存在的興趣點，提取關于興趣點的特征（通常稱為計算機視覺中的圖像描述符），并確定對象的姿態。 多年來，SIFT 的使用擴展到不僅提取興趣點，而且遍及整個圖像的特征。SIFT 特征提取過程非常類似于另一種稱為 Histogram of Oriented Gradients （HOG）的技術。它們都計算梯度方向的直方圖。現在我們詳細地描述一下。 ## 人工特征提取：SIFT 與 HOG ### 圖像梯度 要比原始像素值做得更好，我們必須以某種方式將像素組織成更多信息單元。相鄰像素之間的差異通常是非常有用的特征。通常情況下像素值在對象的邊界處是不同，當存在陰影、圖案內或紋理表面時。相鄰像素之間的差值稱為圖像梯度。 計算圖像梯度的最簡單的方法是分別計算圖像沿水平（`X`）和垂直（`Y`）軸的差異，然后將它們合成為二維矢量。這涉及兩個 1D 差分操作，可以用矢量掩模或濾波器方便地表示。掩碼`(1, 0, -1)`可以得到在左像素和右像素之間的差異或者上像素和下像素之間的差異，取決于我們應用掩碼的方向。當然也有二維梯度濾波器。但在本例中，1D 濾波器就足夠了。 為了對圖像應用濾波器，我們執行卷積。它涉及翻轉濾波器和內積與一小部分的圖像，然后移動到下一個塊。卷積在信號處理中很常見。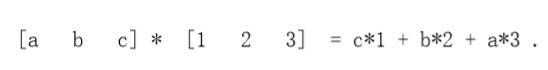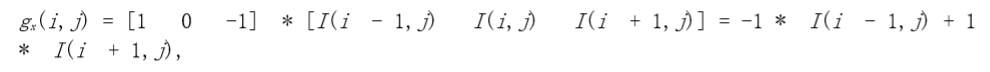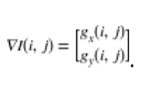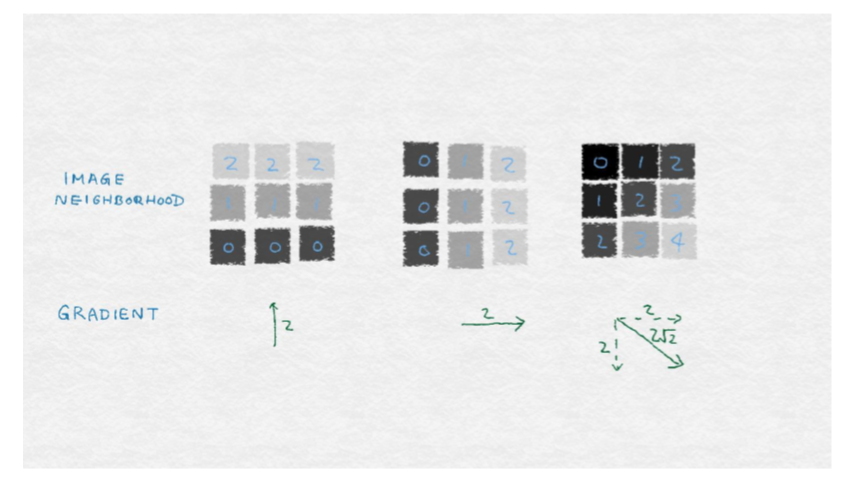我們將使用`*`來表示操作：  在像素點（i，j）的x梯度和y梯度為：  他們一起組成了梯度：  向量可以通過它的方向和大小來完全描述。梯度的大小等于梯度的歐幾里得范數，這表明像素值在像素周圍變化得多大。梯度的位置或方向取決于水平方向和垂直方向上的變化的相對大小；圖 8-2 說明了這些數學概念。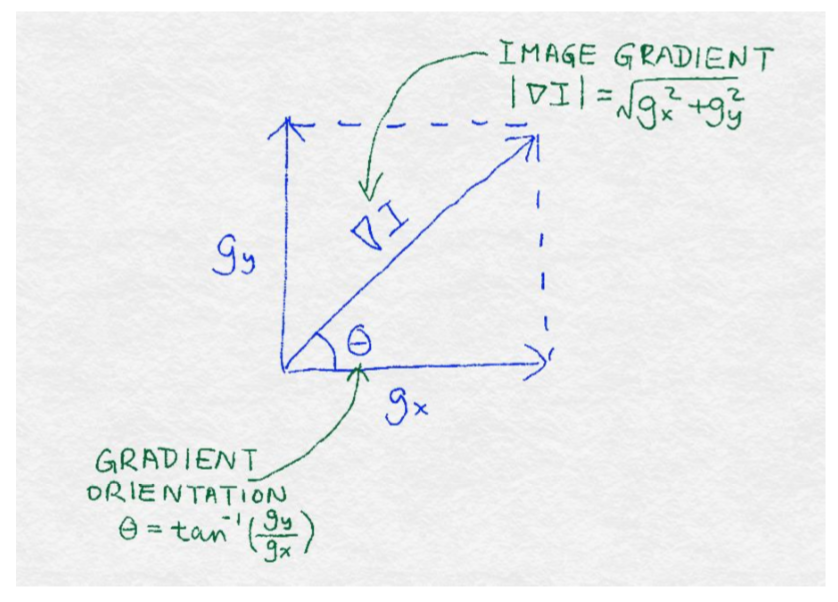  圖8—3展出了由垂直和水平梯度組成的圖像梯度的示例。每個示例是一個 9 像素的圖像。每個像素用灰度值標記。（較小的數字對應于較深的顏色）中心像素的梯度顯示在每個圖像下面。左側的圖像包含水平條紋，其中顏色僅垂直變化。因此，水平梯度為零，梯度垂直為非零。中心圖像包含垂直條紋，因此水平梯度為零。右邊的圖像包含對角線條紋，斜率也是對角線。  它們能在真實的圖像上發揮作用嗎？在例 8-1 中，我們使用圖 8-4 所示的貓的水平和垂直梯度上來實驗。由于梯度是在原始圖像的每個像素位置計算的，所以我們得到兩個新的矩陣，每個矩陣可以被可視化為圖像。  例 8-1 ```python import matplotlib.pyplot as plt import numpy as np from skimage import data, color # Load the example image and turn it into grayscale image = color.rgb2gray(data.chelsea()) # Compute the horizontal gradient using the centered 1D filter # This is equivalent to replacing each non-border pixel with the # difference between its right and left neighbors. The leftmost # and rightmost edges have a gradient of 0. gx = np.empty(image.shape, dtype=np.double) gx[:, 0] = 0 gx[:, -1] = 0 gx[:, 1:-1] = image[:, :-2] - image[:, 2:] # Same deal for the vertical gradient gy = np.empty(image.shape, dtype=np.double) gy[0, :] = 0 gy[-1, :] = 0 gy[1:-1, :] = image[:-2, :] - image[2:, :] # Matplotlib incantations fig, (ax1, ax2, ax3) = plt.subplots(3, 1,figsize=(5, 9),sharex=True,sharey=True) ax1.axis('off') ax1.imshow(image, cmap=plt.cm.gray) ax1.set_title('Original image') ax1.set_adjustable('box-forced') ax2.axis('off') ax2.imshow(gx, cmap=plt.cm.gray) ax2.set_title('Horizontal gradients') ax2.set_adjustable('box-forced') ax3.axis('off') ax3.imshow(gy, cmap=plt.cm.gray) ax3.set_title('Vertical gradients') ax3.set_adjustable('box-forced') ``` 注意，水平梯度提取出強烈的垂直模式，如貓眼睛的內邊緣，而垂直梯度則提取強的水平模式，如晶須和眼睛的上下眼瞼。這乍看起來似乎有些矛盾，如果我們仔細考慮一下，這還是有道理的。水平（X）梯度識別水平方向上的變化。強的垂直圖案在大致相同的`X`位置上跨越多個`Y`像素。因此，垂直圖案導致像素值的水平差異。這也是我們的眼睛也能察覺到的。 ## 梯度方向直方圖 單個圖像梯度可以識別圖像鄰域中的微小差異。但是我們的眼睛看到的圖案比那更大。例如，我們看到一整只貓的胡須，而不僅僅是一個小部分。人類視覺系統識別區域中的連續模式。因此，我們咋就圖像梯度鄰域有仍然有很多的工作要做。 我們如何精確地歸納向量？統計學家會回答：“看分布！SIFT 和 HOG 都走這條路。它們計算（正則化）梯度矢量直方圖作為圖像特征。直方圖將數據分成容器并計算每容器中有多少，這是一個（不規范的）經驗分布。規范化確保數和為 1，用數學語言描述為它具有單位 L 范數。 圖像梯度是矢量，矢量可以由兩個分量來表示：方向和幅度。因此，我們仍然需要決定如何設計直方圖來表示這兩個分量。SIFT 和 HOG 提供了一個解決方案，其中圖像梯度被它們的方向角所包括，由每個梯度的大小加權。以下是流程： 1. 將 0° - 360° 分成相等大小的容器。 2. 對于鄰域中的每個像素，將權重W添加到對應于其方向角的容器中。 3. `W`是梯度的大小和其他相關信息的函數。例如，其他相關信息可以是像素到圖像貼片中心的逆距離。其思想是，如果梯度較大，權重應該很大，而圖像鄰域中心附近的像素比遠離像素的像素更大。 4. 正則化直方圖。 圖 8-5 提供了由`4x4`像素的圖像鄰域構成的8個容器的梯度方向直方圖的圖示。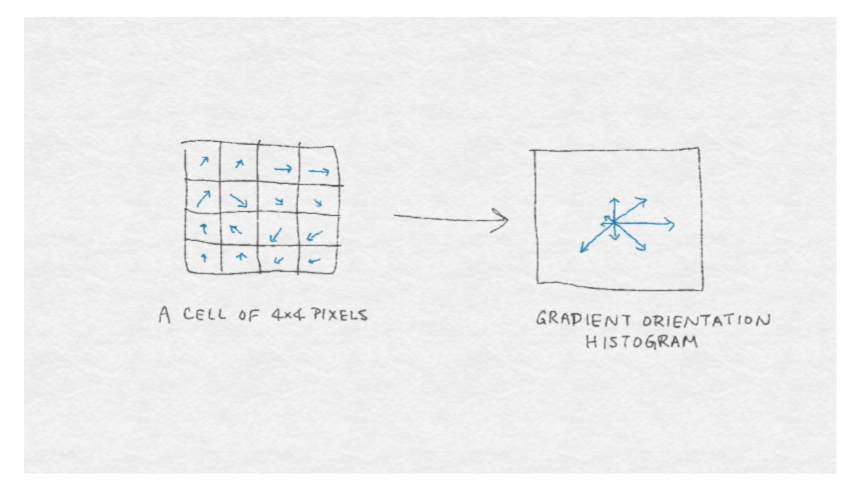  當然，在基本的梯度方向直方圖算法中還有許多選項。像通常一樣，正確的設置可能高度依賴于想要分析的特定圖像。 ### 有多少容器？ 他們的跨度是從 0° - 360°（有符號梯度）還是 0° - 180°（無符號梯度）？ 具有更多的容器導致梯度方向的細粒度量化，因此會保留更多關于原始梯度的信息。但是，有太多的容器是不必要的，并可能導致過度擬合訓練數據。例如，在圖像中識別貓可能不依賴于精確地取向在 3° 的貓的晶須。 還有一個問題，容器是否應該跨越 0 - 360°，這將沿`Y`軸保持梯度，或跨越 0°- 180°，這將不會保留垂直梯度的符號。Dalal 與 Triggs 是 HOG 論文的最初作者，實驗確定從 0 - 180° 跨越的 9 個容器是最好的，而 SIFT 論文推薦了 8 個跨越 0° - 360° 的容器。 ### 使用什么樣的權重函數？ HOG 論文比較各種梯度幅度加權方案：其大小本身、平方、平方根、二值化等等。沒有改變的平面大小在實驗中表現最好。 SIFT 還使用梯度的原始大小。最重要的是，它希望避免圖像描述符在圖像窗口位置的微小變化中的突然變化。因此，它使用從窗口中心測量的高斯距離函數來衡量來自鄰域邊緣的梯度。換言之，梯度幅值乘以高斯函數 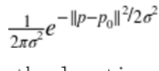，其中`P`是產生梯度的像素的位置，`P0`圖像鄰域的中心位置，并且`σ`為高斯的寬度，`σ`被設置為鄰域半徑的一半。 SIFT 還希望避免從單個圖像梯度方向的微小變化來改變方向直方圖中的大的變化。因此，它使用一個插值技巧，將權重從一個梯度擴展到相鄰的方向箱。特別地，根箱（梯度分配的箱）得到加權幅度的 1 倍的投票。每個相鄰的容器得到 1-D 的投票，其中`D`是來自根容器的直方圖箱單元的差異。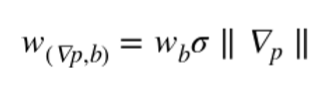 總的來說，SIFT 的單一圖像梯度的投票是  其中 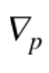 是在箱`b`的像素點`p`的梯度，`Wb`是權值`b`的插值，`σ`是`p`距離中心的高斯距離。 ### 鄰域怎么定義？他們應該怎樣覆蓋圖片？ HOG 和 SIFT 都基于圖像鄰域的兩層表示：首先，將相鄰像素組織成單元，然后將相鄰單元組織成塊。計算每個單元的方向直方圖，并將單元直方圖矢量連接起來，形成整個塊的最終特征描述符。 SIFT 使用`16x16`像素的單元，將其組織成 8 個方向的容器，然后通過`4x4`單元的塊分組，使得圖像鄰域的`4x4x8=128`個特征。 HOG 論文實驗用矩形和圓形形狀的單元和塊。矩形單元稱為 R-HOG。最好的 R-HOG 設置為`8x8`像素的 9 個定向倉，每個分組為`2x2`個單元的塊。圓形窗口稱為 C-HOG，具有由中心單元的半徑確定的變量、單元是否徑向分裂、外單元的寬度等。 無論鄰域如何組織，它們通常重疊形成整個圖像的特征向量。換言之，單元和塊在水平方向和垂直方向上橫移圖像，一次只有幾個像素，以覆蓋整個圖像。 鄰域結構的主要組成部分是多層次的組織和重疊的窗口，其在圖像上移動。在深度學習網絡的設計中使用了相同的成分。 ### 什么樣的歸一化？ 歸一化處理出特征描述符，使得它們具有可比的大小。它是縮放的同義詞，我們在第 4 章中討論過。我們發現，文本特征的特征縮放（以 tf-idf 的形式）對分類精度沒有很大影響。圖像特征與文字區別很大，其對在自然圖像中出現的照明和對比度的變化可能是非常敏感的。例如，在強烈的聚光燈下觀察蘋果的圖像，而不是透過窗戶發出柔和的散射光。即使物體是相同的，圖像梯度也會有非常不同的幅度。為此，計算機視覺中的圖像特征通常從全局顏色歸一化開始，以消除照度和對比度方差。對于 SIFT 和 HOG 來說，結果表明，只要我們對特征進行歸一化，這種預處理是不必要的。 SIFT 遵循歸一化-閾值-歸一化方案。首先，塊特征向量歸一化為單位長度（L2 標準化）。然后，將特征剪輯除以最大值以擺脫極端的照明效果，如從相機的色彩飽和度。最后，將剪切特征再次歸一化到單位長度。 HOG 論文實驗涉及不同的歸一化方案例如 L1 和 L2，包括 SIFT 論文中標歸一化-閾值-歸一化方案。他們發現L1歸一化比其他的方法稍顯不靠譜。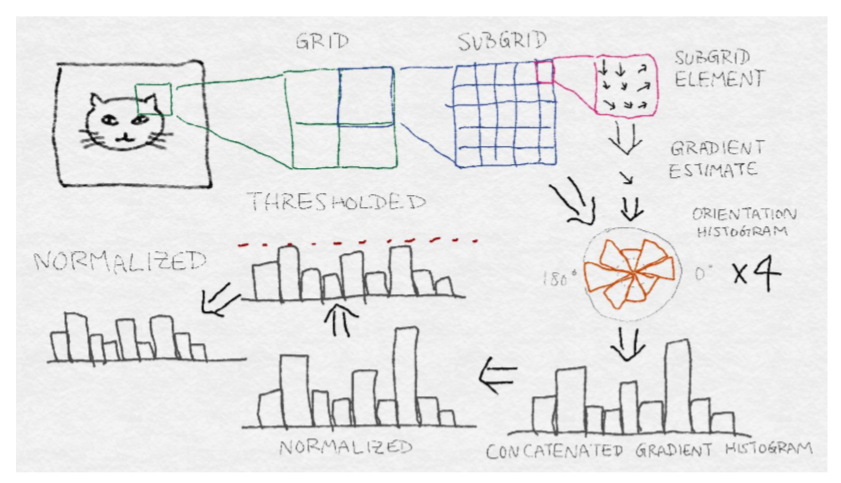 ## SIFT 結構 SIFT 需要相當多的步驟。HOG 稍微簡單，但是遵循許多相同的基本步驟，如梯度直方圖和歸一化。圖 8-6 展示了 SIFT 體系結構。從原始圖像中的感興趣區域開始，首先將區域劃分為網格。然后將每個網格單元進一步劃分為子網格。每個子網格元素包含多個像素，并且每個像素產生梯度。每個子網格元素產生加權梯度估計，其中權重被選擇以使得子網格元素之外的梯度可以貢獻。然后將這些梯度估計聚合成子網格的方向直方圖，其中梯度可以具有如上所述的加權投票。然后將每個子網格的方向直方圖連接起來，形成整個網格的長梯度方向直方圖。（如果網格被劃分為`2x2`子網格，那么將有 4 個梯度方向直方圖拼接成一個。）這是網格的特征向量。從這開始，它經過一個歸一化-閾值-歸一化過程。首先，將向量歸一化為單位范數。然后，將單個值剪輯除以最大閾值。最后，再次對閾值向量進行歸一化處理。這是圖像塊的最終 SIFT 特征描述。  ## 基于深度神經網絡的圖像特征提取 SIFT 和 HOG 在定義良好的圖像特征方面走了很久。然而，計算機視覺的最新成果來自一個非常不同的方向：深度神經網絡模型。這一突破發生在 2012 的 ImageNet 挑戰中，多倫多大學的一組研究人員幾乎將前一年的獲獎者的錯誤率減半。他們強調他們的方法是“深度學習”。與以前的神經網絡模型不同，最新一代包含許多層疊在彼此之上的神經網絡層和變換。ImageNet 2012 的獲獎模型隨后被稱為 AlexNet ，其神經網絡有 13 層。之后 IMANET 2014 的獲勝者有 27 層。 從表面上看，疊層神經網絡的機制與 SIFT 和 HOG 的圖像梯度直方圖有很大的不同。但是 AlxNETA 的可視化顯示，前幾層本質上是計算邊緣梯度和其他簡單的操作，很像 SIFT 和 HOG。隨后的層將局部模式組合成更全局的模式。最終的結果是一個比以前更強大的特征提取器。 堆疊層的神經網絡（或任何其他分類模型）的基礎思想不是新的。但是，訓練這種復雜的模型需要大量的數據和強大的計算能力，這是直到最近才有的。ImageNet 數據集包含來自 1000 個類的 120 萬個圖像的標記集。現代 GPU 加速了矩陣向量計算，這是許多機器學習模型的核心，包括神經網絡。深度學習方法的成功取決于大量可用的數據和大量的 GPU 小時。 深度學習架構可以由若干類型的層組成。例如，AlxNETs 包含卷積、全連接層、歸一化層和最大池化層。現在我們將依次查看每一層的內容。 ## 全連接層 所有神經網絡的核心是輸入的線性函數。我們在第4章中遇到的邏輯回歸是神經網絡的一個示例。全連接的神經網絡只是所有輸入特征的一組線性函數。回想一個線性函數可以被寫為輸入特征向量與權重向量之間的內積，加上一個可能的常數項。線性函數的集合可以表示為矩陣向量乘積，其中權重向量成為權重矩陣。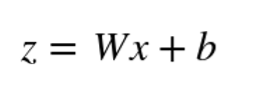 ### 全連接層的數學定義  `W`的每一行是將整個輸入向量`X`映射成`Z`中的單個輸出的權重向量。`b`是表示每個神經元恒定偏移（或偏置）的標量。 全連接層之所以如此命名，是因為在每一個輸入都要在每個輸出中使用。在數學上，這意味著對矩陣`W`中的值沒有限制。（如我們將很快看到的，卷積層僅利用每個輸出的一小部分輸入。）在圖中，一個完全連接的神經網絡可以由一個完整的二部圖表示，其中前一層的每個結點輸出都連接到下一層的每個輸入。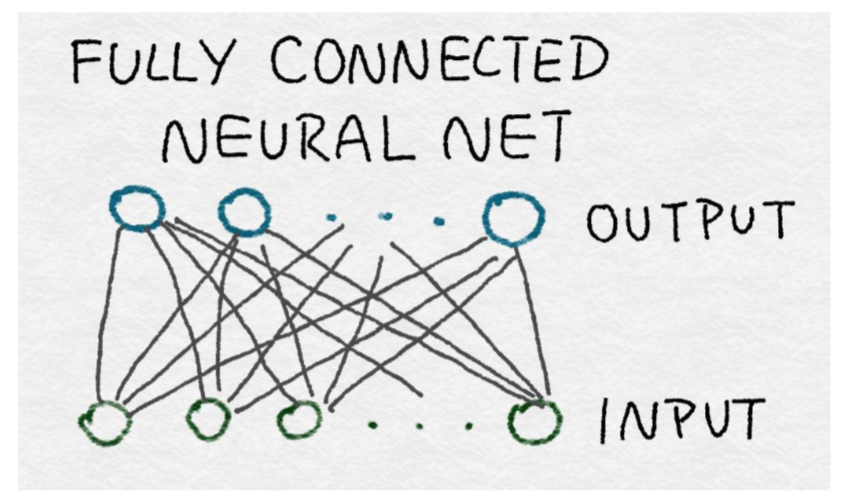  全連接層包含盡可能多的參數。因此，它們是昂貴的。這種密集連接允許網絡檢測可能涉及所有輸入的全局模式。由于這個原因，AlexNet 的最后兩層完全連接。在輸入為條件下輸出仍然是相互獨立的。 ## 卷積層 與全連接層相反，卷積層僅使用每個輸出的輸入子集。通過在輸入上移動窗，每次使用幾個特征產生輸出。為了簡單起見，可以對輸入的不同集合使用相同的權重，而不是重新學習新權重。數學上，卷積算子以兩個函數作為輸入，并產生一個函數作為輸出。它翻轉一個輸入函數，將其移動到另一個函數上，并在每個點上在乘法曲線下輸出總面積。計算曲線下總面積的方法是取其積分。操作符在輸入中是對稱的，這意味著不管我們翻轉第一個輸入還是第二個輸入，輸出都是一樣的。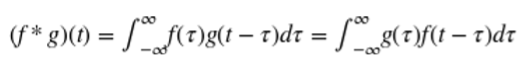 卷積定義為  我們已經看到了一個簡單的卷積的示例，當我們看著圖像梯度（“圖像梯度”）。但是卷積的數學定義似乎仍有點復雜。用信號處理的示例來解釋卷積后的結果是最容易的。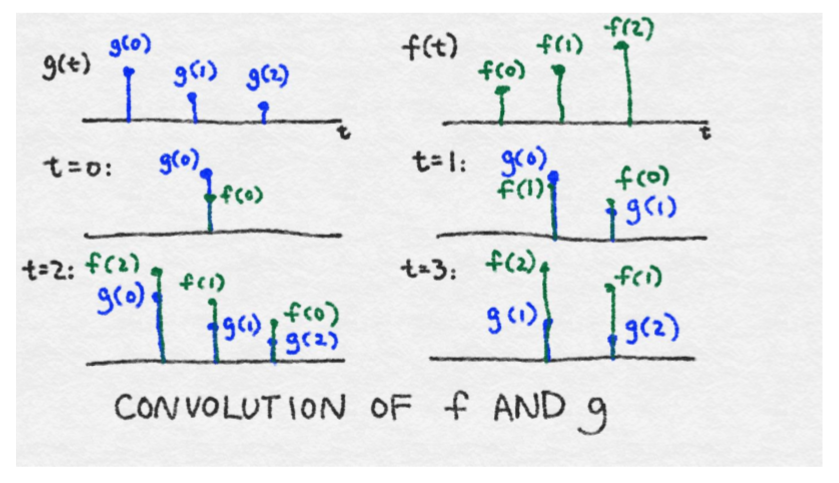 想象一下，我們有一個小黑匣子。為了看到黑匣子的作用，我們通過一個單一的刺激單位。無論輸出看起來如何，我們記錄在一張紙上。我們等到對最初的刺激沒有反應為止。隨時間變化的函數稱為響應函數；我們稱之為響應函數`g(t)`。 想想一下現在我們有一個瘋狂的函數`f(t)`，隨后將它輸入黑盒中。在時間`t=0`時，`f(0)`與黑盒進行通訊，隨后用`f(0)`乘以`g(0)`。在時間`t=1`，`f(1)`進入黑盒，隨后與`g(0)`相乘。在相同的時間，黑盒持續回復信號`f(0)`，它現在是月`g(1)`相乘了。所以在`t=1`時的輸出為`(f(0)*g(1))+(f(1)*g(0))`。在`t=2`時，輸出會變得更復雜，當`f(2)`進入圖片后，這時`f(0)`與`f(1)`持續產生回復。所以在`t=2`時的總輸出為`(f(0)*g(2))+(f(1)*g(1))+(f(2)*g(0))`。通過這種方式，響應函數在時間上有效地被翻轉，其中`τ=0`總是與當前進入黑匣子的信息進行交互，并且響應函數的尾部與先前發生的函數進行交互。圖 8—8 展示了這一過程。到目前為止，為了便于描述，我們已經把時間離散了。在現實中，時間是連續的，所以總和是一個積分。 這個黑箱被稱為線性系統，因為它不比標量乘法和求和更瘋狂。卷積算子清楚地捕捉線性系統的影響。 ### 卷積的思想 卷積算子捕獲線性系統的效果，該線性系統將輸入信號與其響應函數相乘，求出所有過去輸入響應的和。 在上面的示例中，`g(t)`用來表示響應函數，`f(t)`表示輸入。但是由于卷積是對稱的，響應和輸出實際上并不重要。輸出只是兩者的結合。`g(t)`也稱為濾波器。  圖像是二維信號，所以我們需要一個二維濾波器。二維卷積濾波器通過取兩個變量的積分來推廣一維情形。由于數字圖像具有離散像素，卷積積分變成離散和。此外，由于像素的數量是有限的，濾波函數只需要有限數量的元素。在圖像處理中，二維卷積濾波器也被稱為核或掩模。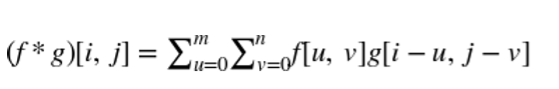 2 維卷積的離散定義  當將卷積濾波器應用于圖像時，我們不需要定義一個覆蓋整個圖像的巨型濾波器。相反，只覆蓋幾個像素的濾波器就夠了，并且在圖像上應用相同的濾波器，并在在水平和垂直像素方向上移動。 因為在圖像中使用相同的濾波器，所以我們只需要定義一組小的參數。權衡是濾波器只能在一個小像素鄰域內吸收信息。換言之，卷積神經網絡識別局部信息而不是全局信息。 ### 卷積濾波器示例 在這個示例中，我們將高斯濾波器應用于圖像。高斯函數在零附近形成光滑對稱的圖形。濾波器在附近函數值產生加權平均值。當應用于圖像時，它具有模糊附近像素值的效果。二維高斯濾波器是由 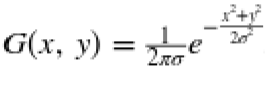 定義的，其中`σ`為高斯函數的標準差，它控制著圖形的寬度。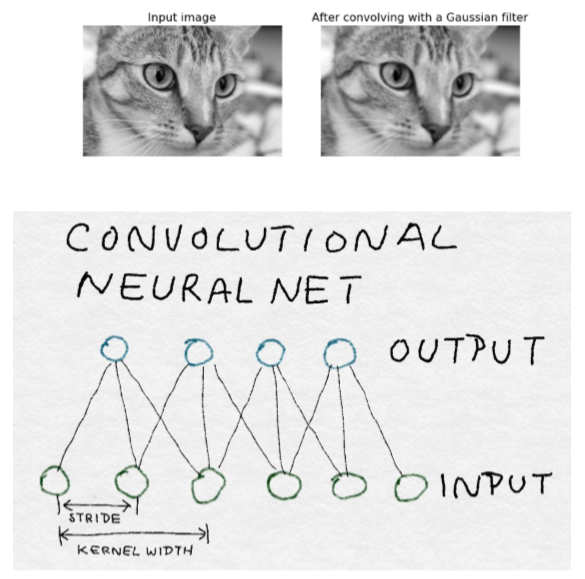 在下面的代碼示例中，我們將首先創建二維高斯濾波器，然后將它與貓圖像進行卷積以產生模糊的貓。注意，這不是計算高斯濾波器的最精確的方法，但它是最容易理解的。采取在每個離散點的加權平均值，而不是簡單的點估計是更好的實現方法。 ```python >>> import numpy as np # First create X, Y meshgrids of size 5x5 on which we compute the Gaussian >>> ind = [-1., -0.5, 0., 0.5, 1.] >>> X,Y = np.meshgrid(ind, ind) >>> X array([[-1. , -0.5, 0. , 0.5, 1. ], [-1. , -0.5, 0. , 0.5, 1. ], [-1. , -0.5, 0. , 0.5, 1. ], [-1. , -0.5, 0. , 0.5, 1. ], [-1. , -0.5, 0. , 0.5, 1. ]]) # G is a simple, unnormalized Gaussian kernel where the value at (0,0) is 1.0 >>> G = np.exp(-(np.multiply(X,X) + np.multiply(Y,Y))/2) >>> G array([[ 0.36787944, 0.53526143, 0.60653066, 0.53526143, 0.36787944], [ 0.53526143, 0.77880078, 0.8824969 , 0.77880078, 0.53526143 ], [ 0.60653066, 0.8824969 , 1. , 0.8824969 , 0. 60653066], [ 0.53526143, 0.77880078, 0.8824969 , 0.77880078, 0.53526143 ], [ 0.36787944, 0.53526143, 0.60653066, 0.53526143, 0.36787944 ]]) >>> from skimage import data, color >>> cat = color.rgb2gray(data.chelsea()) >>> from scipy import signal >>> blurred_cat = signal.convolve2d(cat, G, mode='valid') >>> import matplotlib.pyplot as plt >>> fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(10,4), ... sharex=True, sharey=True) >>> ax1.axis('off') >>> ax1.imshow(cat, cmap=plt.cm.gray) >>> ax1.set_title('Input image') >>> ax1.set_adjustable('box-forced') >>> ax2.axis('off') >>> ax2.imshow(blurred_cat, cmap=plt.cm.gray) >>> ax2.set_title('After convolving with a Gaussian filter')>>> ax2.set_adjustable('box-forced') ```  AlxNet 中的卷積層是三維的。換言之，它們對前一層的三維像素進行操作。第一卷積神經網絡采用原始 RGB 圖像，并在所有三個顏色通道中學習用于局部圖像鄰域的卷積濾波器。隨后的層跨越空間和內核尺寸將其作為輸入像素。 ## 整流線性單元（Relu）變換 神經網絡的輸出通常通過另一個非線性變換，也稱為激活函數。常見的選擇是 tanh 函數（在 -1 和 1 之間有界的光滑非線性函數），sigmoid 函數（0 到 1 之間的平滑非線性函數），或者稱為整流線性單元的函數（Relu）。Relu 是一個線性函數的簡單變化，其中負部分被歸零。換言之，它修剪了負值，但留下無窮的正邊界。Relu 的范圍從 0 到無窮大。 整流線性單元（Relu）是線性函數，負部分歸零。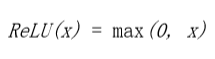  tanh 函數，在 -1 和 1 之間有界的光滑非線性函數。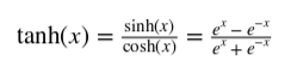  sigmoid 函數，0 到 1 之間的平滑非線性函數。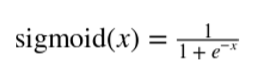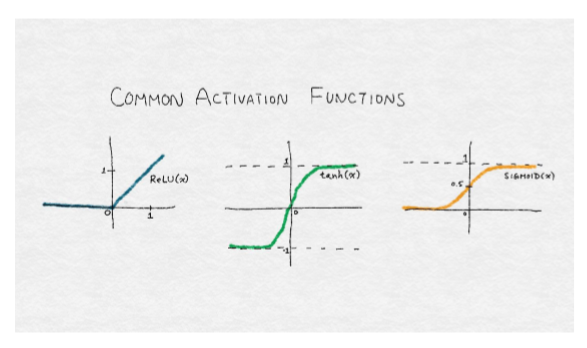   Relu 變換對原始圖像或高斯濾波器等非負函數沒有影響。然而，經過訓練的神經網絡，無論是完全連接的還是卷積的，都有可能輸出負值。AlxNet 使用 Relu 代替其他變換，在訓練過程中可以更快的收斂，它適用于每一個卷積和全連接層。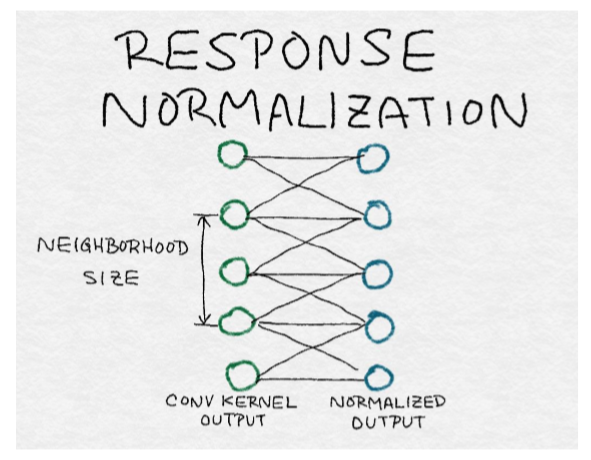 ## 響應歸一化層 在第 4 章和本章之前的討論之后，歸一化對大家來說應該是一個熟悉的概念。歸一化將個體輸出通過集體總響應的函數來劃分。因此，理解歸一化的另一種方式是，它在鄰居之間產生競爭，因為現在每個輸出的強度都相對于其鄰居進行測量。AlexNet 在不同內核的每個位置上歸一化輸出。 局部響應歸一化引起相鄰核之間的競爭  其中，`Xk`是第`k`個核的輸出，yk是相對于鄰域中的其他核的歸一化響應。對每個輸出位置分別執行歸一化。換言之，對于每個輸出位置`(i, j)`，在附近的卷積核輸出上進行歸一化。注意，這與在圖像鄰域或輸出位置上的歸一化不相同。內核鄰域的尺寸`c`、`α`和`β`的大小超參數都是通過圖像驗證集調整的。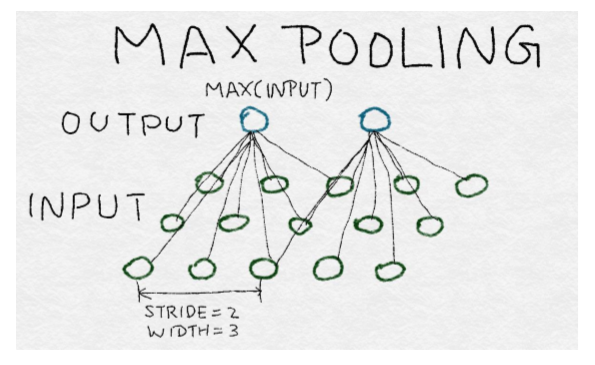  ## 池化層 池化層將多個輸入組合成單個輸出。當卷積濾波器在圖像上移動時，它為其尺寸下的每個鄰域生成輸出。池化層迫使局部圖像鄰域產生一個值而不是許多值。這減少了在深度學習網絡的中間層中的輸出數量，這有效地減少了過擬合訓練數據的概率。 有多種方法匯集輸入：平均，求和（或計算一個廣義范數），或取最大值。池化層通過圖像或中間輸出層移動。Alxnet 使用最大池化層，以 2 像素（或輸出）的步幅移動圖像，并在 3 個鄰居之間匯集。  ## AlexNet 的結構 AlexNet 包含 5 個卷積層、2 個響應歸一化層、3 個最大池化層和 2 個全連接層。與最終分類輸出層一起，模型中共有 13 層神經網絡層，形成8層層組。詳情請參閱圖 8-12。 輸入圖像首先被縮放到`256x256`像素。輸入實際上是`224x224`大小的隨機圖像，具有 3 個顏色通道。前兩個卷積層各有一個響應歸一化層和一個最大池化層，最后一個卷積層接著是最大池化層。原始文件用兩個 GPU 來分割訓練數據和計算。層之間的通信主要限于在相同的 GPU 內。在層組 2 和 3 之間，并且在層組 5 之后是例外的。在這些邊界點，下一層從兩個 GPU 上的前一層的內核的像素作為輸入。每個中間層都使用 Relu 變換。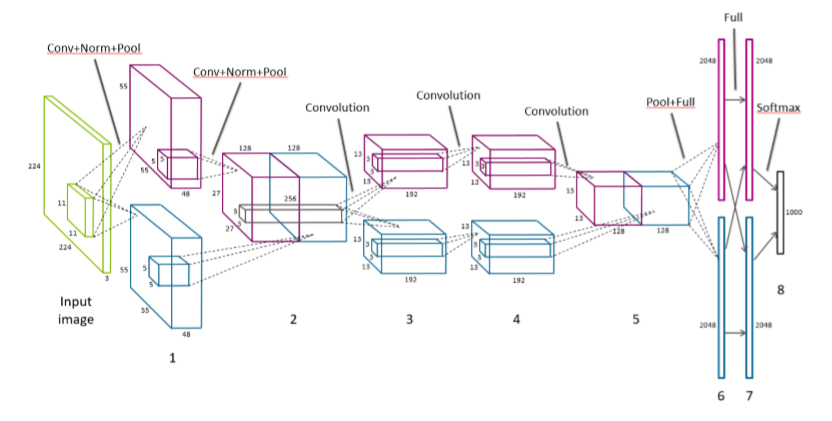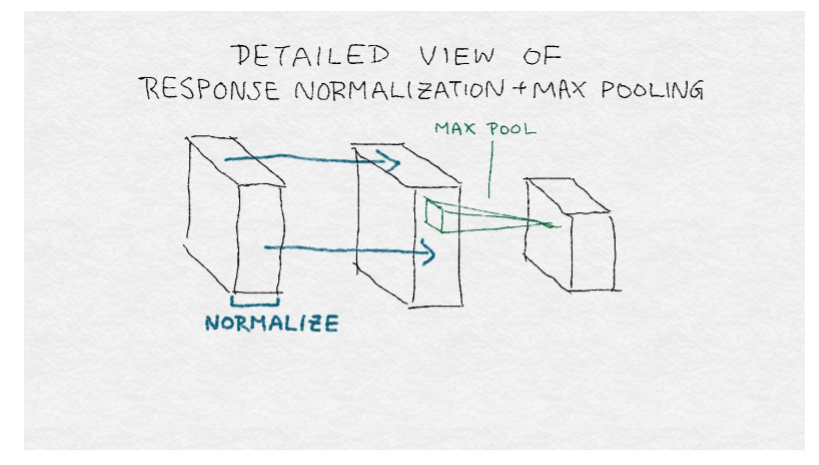   注意 AlexNet 是 SIFT/HOG 特征提取器的梯度直方圖標準化規范化體系結構（參見圖8 -6），但具有更多的層。（這就是“深度學習”中的“深度”）不同于 SIFT/HOG，卷積核和全連接權值是從數據中學習的，而不是預定義的。此外，SIFT 中的歸一化步驟在整個圖像區域上遍及特征向量執行，而 AlexNet 中的響應歸一化層在卷積核上歸一化。 深入的來看，模型從局部圖像鄰域中提取特征開始。每個后續層建立在先前層的輸出上，有效地覆蓋原始圖像的相繼較大區域。因此，即使前五個卷積層都具有相當小的內核寬度，后面的層依然能夠制定更多的全局特征。端部的全連接層是最具全局性的。 盡管特征的要點在概念上是清晰的，但是很難想象每個層挑選出的實際特征。圖 8- 14 和圖 8-15 顯示了由特征型學習的前兩層卷積核的可視化。第一層包括在不同的方向上的灰度邊緣和紋理的檢測器，以及顏色斑點和紋理。第二層似乎是各種光滑圖案的檢測器。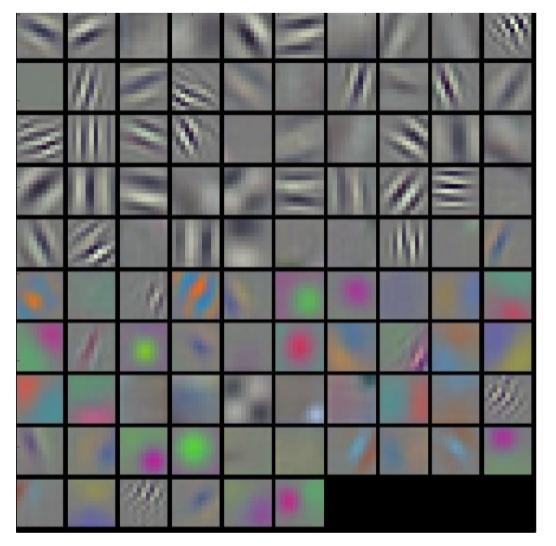   盡管該領域有巨大的進步，圖像特征仍然是一門藝術而不是科學。十年前，人工制作的特征提取步驟結合了圖像梯度、邊緣檢測、定位、空間提示、平滑和歸一化等。如今，深度學習架構師構建了封裝相同想法的模型，但是這些參數是從訓練圖像中自動學習的。 ## 總結 接近尾聲，我們在直覺上更好地理解為什么最直接和簡單的圖像特征在執行任務時將永遠不是最有用的，如圖像分類。與其將每個像素表示為原子單位相反，更重要的是考慮像素與它們附近的其他像素之間的關系。我們可以將這些技術如 SIFT 和 HOG 一樣，通過分析鄰域的梯度更好地提取整個圖像的特征，發展技術以適應其他任務。 近年來的又一次飛躍將更深層次的神經網絡應用于計算機視覺，以進一步推動圖像的特征提取。這里要記住的重要一點是，深度學習堆疊了許多層的神經網絡和相互轉換。這些層中的一些，當單獨檢查時，開始梳理出類似的特征，這些特征可以被識別為人類視覺的構建塊：定義線條、梯度、顏色圖。