# 四、特征縮放的效果：從詞袋到 TF-IDF > 譯者：[@gin](https://github.com/tirtile) > > 校對者：[@HeYun](https://github.com/KyrieHee) 字袋易于生成，但遠非完美。假設我們平等的統計所有單詞，有些不需要的詞也會被強調。在第三章提過一個例子，Emma and the raven。我們希望在文檔表示中能強調兩個主要角色。示例中，“Eama”和“raven”都出現了3詞，但是“the”的出現高達8次，“and”出現了次，另外“it”以及“was”也都出現了4詞。僅僅通過簡單的頻率統計，兩個主要角色并不突出。這是有問題的。 其他的像是“magnificently,” “gleamed,” “intimidated,” “tentatively,” 和“reigned,”這些輔助奠定段落基調的詞也是很好的選擇。它們表示情緒，這對數據科學家來說可能是非常有價值的信息。 所以，理想情況下，我們會傾向突出對有意義單詞的表示。 ## Tf-Idf: 詞袋的小轉折 Tf-Idf 是詞袋的一個小小的轉折。它表示詞頻-逆文檔頻。tf-idf不是查看每個文檔中每個單詞的原始計數，而是查看每個單詞計數除以出現該單詞的文檔數量的標準化計數。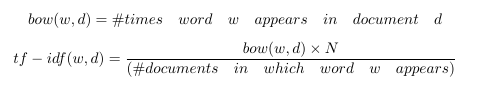  N代表數據集中所有文檔的數量。分數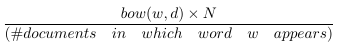就是所謂的逆文件頻率。如果一個單詞出現在許多文檔中，則其逆文檔頻率接近1。如果單詞出現在較少文檔中，則逆文檔頻率要高得多。 或者，我們可以對原始逆文檔頻率進行對數轉換，可以將1變為0，并使得較大的數字（比1大得多）變小。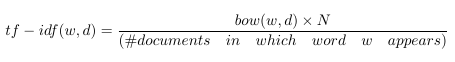（稍后更多內容） 如果我們定義 tf-idf 為：  那么每個文檔中出現的單詞都將被有效清零，并且只出現在少數文檔中的單詞的計數將比以前更大。 讓我們看一些圖片來了解它的具體內容。圖4-1展示了一個包含4個句子的簡單樣例：“it is a puppy,” “it is a cat,” “it is a kitten,” 以及 “that is a dog and this is a pen.” 我們將這些句子繪制在“puppy”，“cat”以及“is”三個詞的特征空間上。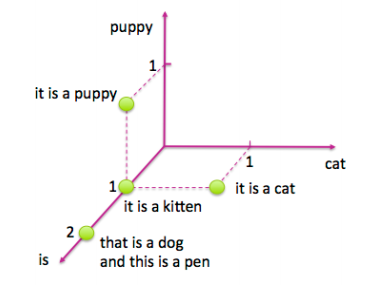  <center><h5>圖 4-1: 關于貓和狗的四個句子</h5></center> 現在讓我們看看對逆文檔頻進行對數變換之后，相同四個句子的tf-idf表示。 圖4-2顯示了相應特征空間中的文檔。可以注意到，單詞“is”被有效地消除，因為它出現在該數據集中的所有句子中。另外，單詞“puppy”和“cat”都只出現在四個句子中的一個句子中，所以現在這兩個詞計數得比之前更高（log(4)=1.38...>1）。因此tf-idf使罕見詞語更加突出，并有效地忽略了常見詞匯。它與第3章中基于頻率的濾波方法密切相關，但比放置嚴格截止閾值更具數學優雅性。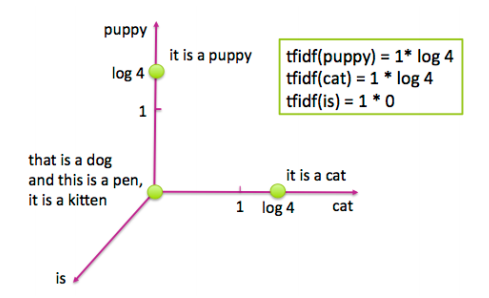  <center><h5>Figure 4-2: 圖4-1中四個句子的Tf-idf表示</h5></center> ## Tf-Idf的含義 Tf-idf使罕見的單詞更加突出，并有效地忽略了常見單詞。 ## 測試 Tf-idf通過乘以一個常量來轉換字數統計特性。因此，它是特征縮放的一個例子，這是第2章介紹的一個概念。特征縮放在實踐中效果有多好？ 我們來比較簡單文本分類任務中縮放和未縮放特征的表現。 coding時間到！ 本次實踐， 我們依舊采用了Yelp評論數據集。Yelp數據集挑戰賽第6輪包含在美國六個城市將近一百六十萬商業評論。 ### 樣例4-1：使用python加載和清洗Yelp評論數據集 ``` import json import pandas as pd ## Load Yelp Business data biz_f = open('data/yelp/v6/yelp_dataset_challenge_academic_dataset/yelp_academic_datase ess.json') biz_df = pd.DataFrame([json.loads(x) for x in biz_f.readlines()]) biz_f.close() ## Load Yelp Reviews data review_file = open('data/yelp/v6/yelp_dataset_challenge_academic_dataset/yelp_academic_dataset_review.json') review_df = pd.DataFrame([json.loads(x) for x in review_file.readlines()]) review_file.close() # Pull out only Nightlife and Restaurants businesses two_biz = biz_df[biz_df.apply(lambda x: 'Nightlife' in x['categories'] or 'Restaurants' in x['categories'],axis=1)] # Join with the reviews to get all reviews on the two types of business twobiz_reviews = two_biz.merge(review_df, on='business_id', how='inner') # Trim away the features we won't use twobiz_reviews = twobiz_reviews[['business_id', 'name', 'stars_y', 'text', 'categories']] # Create the target column--True for Nightlife businesses, and False otherwise two_biz_reviews['target'] = twobiz_reviews.apply(lambda x: 'Nightlife' in x['categories'],axis=1) ``` ## 建立分類數據集 讓我們看看是否可以使用評論來區分餐廳或夜生活場所。為了節省訓練時間，僅使用一部分評論。這兩個類別之間的評論數目有很大差異。這是所謂的類不平衡數據集。對于構建模型來說，不平衡的數據集存在著一個問題:這個模型會把大部分精力花費在比重更大的類上。由于我們在這兩個類別都有大量的數據，解決這個問題的一個比較好方法是將數目較大的類（餐廳）進行下采樣，使之與數目較小的類（夜生活）數目大致相同。下面是一個示例工作流程。 1. 隨機抽取10%夜生活場所評論以及2.1%的餐廳評論（選取合適的百分比使得每個種類的數目大致一樣） 2. 將數據集分成比例為7：3的訓練集和測試集。在這個例子里，訓練集包括29，264條評論，測試集有12542條。 3. 訓練數據包括46，924個不同的單詞，這是詞袋表示中特征的數量。 ### 樣例4-2：創建一個分類數據集 ``` # Create a class-balanced subsample to play with nightlife = twobiz_reviews[twobiz_reviews.apply(lambda x: 'Nightlife' in x['categories'], axis=1)] restaurants = twobiz_reviews[twobiz_reviews.apply(lambda x: 'Restaurants' in x['categories'], axis=1)] nightlife_subset = nightlife.sample(frac=0.1, random_state=123) restaurant_subset = restaurants.sample(frac=0.021, random_state=123) combined = pd.concat([nightlife_subset, restaurant_subset]) # Split into training and test data sets training_data, test_data = modsel.train_test_split(combined, train_size=0.7, random_state=123) training_data.shape # (29264, 5) test_data.shape # (12542, 5) ``` ## 用tf-idf轉換縮放詞袋 這個實驗的目標是比較詞袋，tf-idf以及L2歸一化對于線性分類的作用。注意，做tf-idf接著做L2歸一化和單獨做L2歸一化是一樣的。所以我們需要只需要3個特征集合：詞袋，tf-idf，以及逐詞進行L2歸一化后的詞袋。 在這個例子中，我們將使用Scikit-learn的CountVectorizer將評論文本轉化為詞袋。所有的文本特征化方法都依賴于標記器（tokenizer），該標記器能夠將文本字符串轉換為標記（詞）列表。在這個例子中，Scikit-learn的默認標記模式是查找2個或更多字母數字字符的序列。標點符號被視為標記分隔符。 ## 測試集上進行特征縮放 特征縮放的一個細微之處是它需要了解我們在實踐中很可能不知道的特征統計，例如均值，方差，文檔頻率，L2范數等。為了計算tf-idf表示，我們不得不根據訓練數據計算逆文檔頻率，并使用這些統計量來調整訓練和測試數據。在Scikit-learn中，將特征變換擬合到訓練集上相當于收集相關統計數據。然后可以將擬合過的變換應用于測試數據。 ### 樣例4-3：特征變換 ``` # Represent the review text as a bag-of-words bow_transform = text.CountVectorizer() X_tr_bow = bow_transform.fit_transform(training_data['text']) X_te_bow = bow_transform.transform(test_data['text']) len(bow_transform.vocabulary_) # 46924 y_tr = training_data['target'] y_te = test_data['target'] # Create the tf-idf representation using the bag-of-words matrix tfidf_trfm = text.TfidfTransformer(norm=None) X_tr_tfidf = tfidf_trfm.fit_transform(X_tr_bow) X_te_tfidf = tfidf_trfm.transform(X_te_bow) # Just for kicks, l2-normalize the bag-of-words representation X_tr_l2 = preproc.normalize(X_tr_bow, axis=0) X_te_l2 = preproc.normalize(X_te_bow, axis=0) ``` 當我們使用訓練統計來衡量測試數據時，結果看起來有點模糊。測試集上的最小-最大比例縮放不再整齊地映射到零和一。L2范數，平均數和方差統計數據都將顯得有些偏離。這比缺少數據的問題好一點。例如，測試集可能包含訓練數據中不存在的單詞，并且對于新的單詞沒有相應的文檔頻。通常的解決方案是簡單地將測試集中新的單詞丟棄。這似乎是不負責任的，但訓練集上的模型在任何情況下都不會知道如何處理新詞。一種稍微不太好的方法是明確地學習一個“垃圾”單詞，并將所有罕見的頻率單詞映射到它，即使在訓練集中也是如此，正如“罕見詞匯”中所討論的那樣。 ## 使用邏輯回歸進行分類 邏輯回歸是一個簡單的線性分類器。通過對輸入特征的加權組合，輸入到一個sigmoid函數。sigmoid函數將任何實數平滑的映射到介于0和1之間。如圖4-3繪制sigmoid函數曲線。由于邏輯回歸比較簡單，因此它通常是最先接觸的分類器。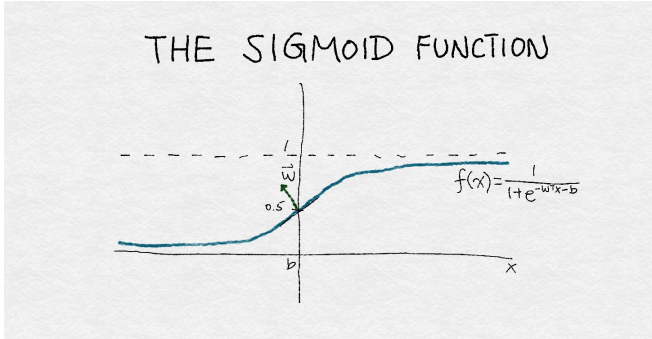  <center><h5>Figure 4-3: sigmoid函數</h5></center> 圖4-3是sigmoid函數的插圖。該函數將輸入的實數x轉換為一個0到1之間的數。它有一組參數w，表示圍繞中點0.5增加的斜率。截距項b表示函數輸出穿過中點的輸入值。如果sigmoid輸出大于0.5，則邏輯分類器將預測為正例，否則為反例。通過改變w和b，可以控制決策的改變，以及決策響應該點周圍輸入值變化的速度。 ### 樣例4-4：使用默認參數訓練邏輯回歸分類器 ``` def simple_logistic_classify(X_tr, y_tr, X_test, y_test, description): ## Helper function to train a logistic classifier and score on test data m = LogisticRegression().fit(X_tr, y_tr) s = m.score(X_test, y_test) print ('Test score with', description, 'features:', s) return m m1 = simple_logistic_classify(X_tr_bow, y_tr, X_te_bow, y_te, 'bow') m2 = simple_logistic_classify(X_tr_l2, y_tr, X_te_l2, y_te, 'l2-normalized') m3 = simple_logistic_classify(X_tr_tfidf, y_tr, X_te_tfidf, y_te, 'tf-idf') # Test score with bow features: 0.775873066497 # Test score with l2-normalized features: 0.763514590974 # Test score with tf-idf features: 0.743182905438 ``` 矛盾的是，結果表明最準確的分類器是使用BOW特征的分類器。出乎意料我們之外。事實證明，造成這種情況的原因是沒有很好地“調整”分類器，這是比較分類器時一個常見的錯誤。 ## 使用正則化調整邏輯回歸 邏輯回歸有些華而不實。 當特征的數量大于數據點的數量時，找到最佳模型的問題被認為是欠定的。 解決這個問題的一種方法是在訓練過程中增加額外的約束條件。 這就是所謂的正則化，技術細節將在下一節討論。 邏輯回歸的大多數實現允許正則化。為了使用這個功能，必須指定一個正則化參數。正則化參數是在模型訓練過程中未自動學習的超參數。相反，他們必須手動進行調整，并將其提供給訓練算法。這個過程稱為超參數調整。（有關如何評估機器學習模型的詳細信息，請參閱評估機器學習模型（Evaluating Machine Learning Models））.調整超參數的一種基本方法稱為網格搜索：指定一個超參數值網格，并且調諧器以編程方式在網格中搜索最佳超參數設置 格。 找到最佳超參數設置后，使用該設置對整個訓練集進行訓練，并比較測試集上這些同類最佳模型的性能。 ## 重點：比較模型時調整超參數 比較模型或特征時，調整超參數非常重要。 軟件包的默認設置將始終返回一個模型。 但是除非軟件在底層進行自動調整，否則很可能會返回一個基于次優超參數設置的次優模型。 分類器性能對超參數設置的敏感性取決于模型和訓練數據的分布。 邏輯回歸對超參數設置相對穩健（或不敏感）。 即便如此，仍然有必要找到并使用正確的超參數范圍。 否則，一個模型相對于另一個模型的優點可能僅僅是由于參數的調整，并不能反映模型或特征的實際表現。 即使是最好的自動調整軟件包仍然需要指定搜索的上限和下限，并且找到這些限制可能需要幾次手動嘗試。 在本例中，我們手動將邏輯正則化參數的搜索網格設置為{1e-5，0.001，0.1，1，10，100}。 上限和下限花費了幾次嘗試來縮小范圍。 表4-1給出了每個特征集合的最優超參數設置。 <center><h5>Table4-1.對夜場和餐廳的Yelp評論進行邏輯回歸的最佳參數設置</h5></center> Method | L2 Regularization --------|----------- BOW | 0.1 L2-normalized| 10 TF-IDF | 0.01 我們也想測試tf-idf和BOW之間的精度差異是否是由于噪聲造成的。 為此，我們使用k折交叉驗證來模擬具有多個統計獨立的數據集。它將數據集分為k個折疊。交叉驗證過程通過分割后的數據進行迭代，使用除除去某一折之外的所有內容進行訓練，并用那一折驗證結果。Scikit-Learn中的GridSearchCV功能通過交叉驗證進行網格搜索。 圖4-4顯示了在每個特征集上訓練的模型的精度測量分布箱線圖。 盒子中線表示中位精度，盒子本身表示四分之一和四分之三分位之間的區域，而線則延伸到剩余的分布。 ### 通過重采樣估計方差 現代統計方法假設底層數據是隨機分布的。 數據導出模型的性能測量也受到隨機噪聲的影響。 在這種情況下，基于相似數據的數據集，不止一次進行測量總是比較好的。 這給了我們一個測量的置信區間。 K折交叉驗證就是這樣一種策略。 重采樣是另一種從相同底層數據集生成多個小樣本的技術。 有關重采樣的更多詳細信息，請參見評估機器學習模型。 ### 樣例4-5：使用網格搜索調整邏輯回歸超參數 ``` >>> import sklearn.model_selection as modsel# Specify a search grid, then do 5-fold grid search for each of the feature sets >>> param_grid_ = {'C': [1e-5, 1e-3, 1e-1, 1e0, 1e1, 1e2]# Tune classifier for bag-of-words representation >>> bow_search = modsel.GridSearchCV(LogisticRegression(), cv=5, param_grid=param_grid_) >>> bow_search.fit(X_tr_bow, y_tr)# Tune classifier for L2-normalized word vector >>> l2_search = modsel.GridSearchCV(LogisticRegression(), cv=5, param_grid=param_grid_) >>> l2_search.fit(X_tr_l2, y_tr)# Tune classifier for tf-idf >>> tfidf_search = modsel.GridSearchCV(LogisticRegression(), cv=5, param_grid=param_grid_) >>> tfidf_search.fit(X_tr_tfidf, y_tr) # Let's check out one of the grid search outputs to see how it went >>> bow_search.cv_results_{'mean_fit_time': array([ 0.43648252, 0.94630651, 5.64090128, 15.31248307, 31.47010217, 42.44257565]), 'mean_score_time': array([ 0.00080056, 0.00392466, 0.00864897, 0.00784755, 0.01192751, 0.0072515 ]), 'mean_test_score': array([ 0.57897075, 0.7518111 , 0.78283898, 0.77381766, 0.75515992, 0.73937261]), 'mean_train_score': array([ 0.5792185 , 0.76731652, 0.87697341, 0.94629064, 0.98357195, 0.99441294]), 'param_C': masked_array(data = [1e-05 0.001 0.1 1.0 10.0 100.0], mask = [False False False False False False], fill_value = ?), 'params': ({'C': 1e-05}, {'C': 0.001}, {'C': 0.1}, {'C': 1.0}, {'C': 10.0}, {'C': 100.0}), 'rank_test_score': array([6, 4, 1, 2, 3, 5]), 'split0_test_score': array([ 0.58028698, 0.75025624, 0.7799795 , 0.7726341 , 0.75247694, 0.74086095]), 'split0_train_score': array([ 0.57923964, 0.76860316, 0.87560871, 0.94434003, 0.9819308 , 0.99470312]), 'split1_test_score': array([ 0.5786776 , 0.74628396, 0.77669571, 0.76627371, 0.74867589, 0.73176149]), 'split1_train_score': array([ 0.57917218, 0.7684849 , 0.87945837, 0.94822946, 0.98504976, 0.99538678]), 'split2_test_score': array([ 0.57816504, 0.75533914, 0.78472578, 0.76832394, 0.74799248, 0.7356911 ]), 'split2_train_score': array([ 0.57977019, 0.76613558, 0.87689548, 0.94566657, 0.98368288, 0.99397719]), 'split3_test_score': array([ 0.57894737, 0.75051265, 0.78332194, 0.77682843, 0.75768968, 0.73855092]), 'split3_train_score': array([ 0.57914745, 0.76678626, 0.87634546, 0.94558346, 0.98385443, 0.99474628]), 'split4_test_score': array([ 0.57877649, 0.75666439, 0.78947368, 0.78503076, 0.76896787, 0.75 ]), 'split4_train_score': array([ 0.57876303, 0.7665727 , 0.87655903, 0.94763369, 0.98334188, 0.99325132]), 'std_fit_time': array([ 0.03874582, 0.02297261, 1.18862097, 1.83901079, 4.21516797, 2.93444269]), 'std_score_time': array([ 0.00160112, 0.00605009, 0.00623053, 0.00698687, 0.00713112, 0.00570195]), 'std_test_score': array([ 0.00070799, 0.00375907, 0.00432957, 0.00668246, 0.00771557, 0.00612049]), 'std_train_score': array([ 0.00032232, 0.00102466, 0.00131222, 0.00143229, 0.00100223, 0.00073252])} ######## # Plot the cross validation results in a box-and-whiskers plot to # visualize and compare classifier performance ######## >>> search_results = pd.DataFrame.from_dict({'bow': bow_search.cv_results_['mean_test_score'], 'tfidf': tfidf_search.cv_results_['mean_test_score'], 'l2': l2_search.cv_results_['mean_test_score']}) # Our usual matplotlib incantations. 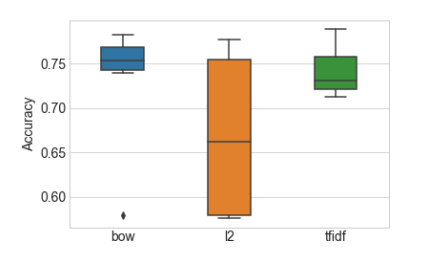Seaborn is used here to make # the plot pretty >>> import matplotlib.pyplot as plt >>> import seaborn as sns >>> sns.set_style("whitegrid") >>> ax = sns.boxplot(data=search_results, width=0.4) >>> ax.set_ylabel('Accuracy', size=14) >>> ax.tick_params(labelsize=14) ```  <center><h5>Figure 4-4: 分類器精度在每個特征集和正則化設置下的分布。 準確度是以5折交叉驗證的平均準確度來衡量的</h5></center> <center><h5>Table4-2.每個超參數設置的平均交叉驗證分類器準確度。 星號表示最高精度</h5></center> <center> Regularization Parameter | BOW | normalized| Tf-idf --------|-----------|----------|--------- 0.00001 | 0.578971 | 0.575724 | 0.721638 0.001| 0.751811 | 0.575724 | 0.788648* 0.1 | 0.782839* | 0.589120 | 0.763566 1 | 0.773818 | 0.734247 | 0.741150 10 | 0.755160 | 0.776756*| 0.721467 100 |0.739373 | 0.761106 | 0.712309 </center> 在圖4-4中，L2歸一化后的特征結果看起來非常糟糕。 但不要被蒙蔽了 。準確率低是由于正則化參數設置不恰當造成的 - 實際證明次優超參數會得到相當錯誤的結論。 如果我們使用每個特征集的最佳超參數設置來訓練模型，則不同特征集的測試精度非常接近。 ###示例4-6：最終的訓練和測試步驟來比較不同的特征集 ``` # Train a final model on the entire training set, using the best hyperparamete # settings found previously. Measure accuracy on the test set. >>> m1 = simple_logistic_classify(X_tr_bow, y_tr, X_te_bow, y_te, 'bow', _C=bow_search.best_params_['C']) >>> m2 = simple_logistic_classify(X_tr_l2, y_tr, X_te_l2, y_te, 'l2-normalized', _C=l2_search.best_params_['C']) >>> m3 = simple_logistic_classify(X_tr_tfidf, y_tr, X_te_tfidf, y_te, 'tf-idf', _C=tfidf_search.best_params_['C']) Test score with bow features: 0.78360708021 Test score with l2-normalized features: 0.780178599904 Test score with tf-idf features: 0.788470738319 ``` <center><h5>Table4-3.BOW, Tf-Idf,以及L2正則化的最終分類精度<h5></center> Feature Set |Test Accuracy --------|----------- Bag-of-Words | 0.78360708021 L2 -normalized | 0.780178599904 Tf-Idf | 0.788470738319 適當的調整提高了所有特征集的準確性，并且所有特征集在正則化后進行邏輯回歸得到了相近的準確率。tf-idf模型準確率略高，但這點差異可能沒有統計學意義。 這些結果是完全神秘的。 如果特征縮放效果不如vanilla詞袋的效果好，那為什么要這么做呢？ 如果tf-idf沒有做任何事情，為什么總是要這么折騰？ 我們將在本章的其余部分中探索答案。 ## 深入：發生了什么？ 為了明白結果背后隱含著什么，我們必須考慮模型是如何使用特征的。對于類似邏輯回歸這種線性模型來說，是通過所謂的數據矩陣的中間對象來實現的。 數據矩陣包含以固定長度平面向量表示的數據點。 根據詞袋向量，數據矩陣也被稱為文檔詞匯矩陣。 圖3-1顯示了一個向量形式的詞袋向量，圖4-1顯示了特征空間中的四個詞袋向量。 要形成文檔詞匯矩陣，只需將文檔向量取出，平放，然后將它們堆疊在一起。 這些列表示詞匯表中所有可能的單詞。 由于大多數文檔只包含所有可能單詞的一小部分，因此該矩陣中的大多數都是零，是一個稀疏矩陣。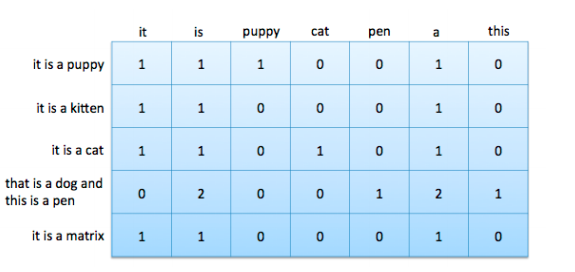  <center><h5>Figure 4-5: 包含5個文檔7個單詞的文檔-詞匯矩陣</h5></center> 特征縮放方法本質上是對數據矩陣的列操作。特別的，tf-idf和L2歸一化都將整列（例如n-gram特征）乘上一個常數。 ## Tf-idf=列縮放 Tf-idf和L2歸一化都是數據矩陣上的列操作。 正如附錄A所討論的那樣，訓練線性分類器歸結為尋找最佳的線性組合特征，這是數據矩陣的列向量。 解空間的特征是列空間和數據矩陣的空間。訓練過的線性分類器的質量直接取決于數據矩陣的零空間和列空間。 大的列空間意味著特征之間幾乎沒有線性相關性，這通常是好的。 零空間包含“新”數據點，不能將其表示為現有數據的線性組合; 大的零空間可能會有問題。（強烈建議希望對諸如線性決策表面，特征分解和矩陣的基本子空間等概念進行的回顧的讀者閱讀附錄A。) 列縮放操作如何影響數據矩陣的列空間和空間？ 答案是“不是很多”。但是在tf-idf和L2歸一化之間有一個小小的差別。 由于幾個原因，數據矩陣的零空間可能很大。 首先，許多數據集包含彼此非常相似的數據點。 這使得有效的行空間與數據集中數據的數量相比較小。 其次，特征的數量可以遠大于數據的數量。 詞袋特別擅長創造巨大的特征空間。 在我們的Yelp例子中，訓練集中有29K條評論，但有47K條特征。 而且，不同單詞的數量通常隨著數據集中文檔的數量而增長。 因此，添加更多的文檔不一定會降低特征與數據比率或減少零空間。 在詞袋模型中，與特征數量相比，列空間相對較小。 在相同的文檔中可能會出現數目大致相同的詞，相應的列向量幾乎是線性相關的，這導致列空間不像它可能的那樣滿秩。 這就是所謂的秩虧。 （就像動物缺乏維生素和礦物質一樣，矩陣秩虧，輸出空間也不會像應該那樣蓬松）。 秩虧行空間和列空間導致模型空間預留過度的問題。 線性模型為數據集中的每個特征配置權重參數。 如果行和列空間滿秩$^1$，那么該模型將允許我們在輸出空間中生成任何目標向量。 當模型不滿秩時，模型的自由度比需要的更大。 這使得找出解決方案變得更加棘手。 可以通過特征縮放來解決數據矩陣的不滿秩問題嗎？ 讓我們來看看。 列空間被定義為所有列向量的線性組合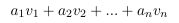：。比方說，特征縮放用一個常數倍來替換一個列向量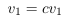，。但是我們仍然可以通過用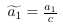來替換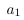，生成原始的線性組合。看起來，特征縮放不會改變列空間的秩。類似地，特征縮放不會影響空間的秩，因為可以通過反比例縮放權重向量中的對應條目來抵消縮放的特征列。 但是，仍然存在一個陷阱。 如果標量為0，則無法恢復原始線性組合;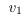消失了。 如果該向量與所有其他列線性無關，那么我們已經有效地縮小了列空間并放大了零空間。 如果該向量與目標輸出不相關，那么這將有效地修剪掉噪聲信號，這是一件好事。 這是tf-idf和L2歸一化之間的關鍵區別。 L2歸一化永遠不會計算零的范數，除非該向量包含全零。 如果向量接近零，那么它的范數也接近于零。 按照小規范劃分將突出向量并使其變大。 另一方面，如圖4-2所示，Tf-idf可以生成接近零的縮放因子。 當這個詞出現在訓練集中的大量文檔中時，會發生這種情況。 這樣的話有可能與目標向量沒有很強的相關性。 修剪它可以使模型專注于列空間中的其他方向并找到更好的解決方案。 準確度的提高可能不會很大，因為很少有噪聲方向可以通過這種方式修剪。 在特征縮放的情況下，L2和tf-idf對于模型的收斂速度確實有促進。 這是該數據矩陣有一個更小的條件數的標志。 事實上，L2歸一化使得條件數幾乎一致。 但情況并非條件數越多，解決方案越好。 在這個實驗中，L2歸一化收斂比BOW或tf-idf快得多。 但它對過擬合也更敏感：它需要更多的正則化，并且對優化期間的迭代次數更敏感。 ## 總結 在本章中，我們使用tf-idf作為入口點，詳細分析特征變換如何影響（或不）模型。Tf-idf是特征縮放的一個例子，所以我們將它的性能與另一個特征縮放方法-L2標準化進行了對比。 結果并不如預期。Tf-idf和L2歸一化不會提高最終分類器的準確度，而不會超出純詞袋。 在獲得了一些統計建模和線性代數處理知識之后，我們意識到了為什么：他們都沒有改變數據矩陣的列空間。 兩者之間的一個小區別是，tf-idf可以“拉伸”字數以及“壓縮”它。 換句話說，它使一些數字更大，其他數字更接近 歸零。 因此，tf-idf可以完全消除無意義的單詞。 我們還發現了另一個特征縮放效果：它改善了數據矩陣的條件數，使線性模型的訓練速度更快。 L2標準化和tf-idf都有這種效果。 總而言之，正確的特征縮放可以有助于分類。 正確的縮放突出了信息性詞語，并降低了常見單詞的權重。 它還可以改善數據矩陣的條件數。 正確的縮放并不一定是統一的列縮放。 這個故事很好地說明了在一般情況下分析特征工程的影響的難度。 更改特征會影響訓練過程和隨后的模型。 線性模型是容易理解的模型。 然而，它仍然需要非常謹慎的實驗方法和大量的深刻的數學知識來區分理論和實際的影響。 對于更復雜的模型或特征轉換來說，這是不可能的。 參考書目 Strang, Gilbert. 2006. Linear Algebra and Its Applications. Brooks Cole Cengage, fourth edition. $^1$ 嚴格地說，矩陣矩陣的行空間和列空間不能都是滿秩的。 兩個子空間的最大秩是m（行數）和n（列數）中的較小者。 這就是我們所說的滿秩。