# 第三章 `ArrayList` > 原文：[Chapter 3 ArrayList](http://greenteapress.com/thinkdast/html/thinkdast004.html) > 譯者：[飛龍](https://github.com/wizardforcel) > 協議：[CC BY-NC-SA 4.0](http://creativecommons.org/licenses/by-nc-sa/4.0/) > 自豪地采用[谷歌翻譯](https://translate.google.cn/) 本章一舉兩得：我展示了上一個練習的解法，并展示了一種使用攤銷分析來劃分算法的方法。 ## 3.1 劃分`MyArrayList`的方法 對于許多方法，我們不能通過測試代碼來確定增長級別。例如，這里是`MyArrayList`的`get`的實現： ```java public E get(int index) { if (index < 0 || index >= size) { throw new IndexOutOfBoundsException(); } return array[index]; } ``` `get`中的每個東西都是常數時間的。所以`get`是常數時間，沒問題。 現在我們已經劃分了`get`，我們可以使用它來劃分`set`。這是我們以前的練習中的`set`： ```java public E set(int index, E element) { E old = get(index); array[index] = element; return old; } ``` 該解決方案的一個有些機智的部分是，它不會顯式檢查數組的邊界；它利用`get`，如果索引無效則引發異常。 `set`中的一切，包括`get`的調用都是常數時間，所以`set`也是常數時間。 接下來我們來看一些線性的方法。例如，以下是我的實現`indexOf`： ```java public int indexOf(Object target) { for (int i = 0; i<size; i++) { if (equals(target, array[i])) { return i; } } return -1; } ``` 每次在循環中，`indexOf`調用`equals`，所以我們首先要劃分`equals`。這里就是： ```java private boolean equals(Object target, Object element) { if (target == null) { return element == null; } else { return target.equals(element); } } ``` 此方法調用`target.equals`；這個方法的運行時間可能取決于`target`或`element`的大小，但它不依賴于該數組的大小，所以出于分析`indexOf`的目的,我們認為這是常數時間。 回到之前的`indexOf`，循環中的一切都是常數時間，所以我們必須考慮的下一個問題是：循環執行多少次？ 如果我們幸運，我們可能會立即找到目標對象，并在測試一個元素后返回。如果我們不幸，我們可能需要測試所有的元素。平均來說，我們預計測試一半的元素，所以這種方法被認為是線性的（除了在不太可能的情況下，我們知道目標元素在數組的開頭）。 `remove`的分析也類似。這里是我的時間。 ```java public E remove(int index) { E element = get(index); for (int i=index; i<size-1; i++) { array[i] = array[i+1]; } size--; return element; } ``` 它使用`get`，這是常數時間，然后從`index`開始遍歷數組。如果我們刪除列表末尾的元素，循環永遠不會運行，這個方法是常數時間。如果我們刪除第一個元素，我們遍歷所有剩下的元素，它們是線性的。因此，這種方法同樣被認為是線性的（除了在特殊情況下，我們知道元素在末尾，或到末尾距離恒定）。 ## 3.2 `add`的劃分 這里是`add`的一個版本，接受下標和元素作為參數： ```java public void add(int index, E element) { if (index < 0 || index > size) { throw new IndexOutOfBoundsException(); } // add the element to get the resizing add(element); // shift the other elements for (int i=size-1; i>index; i--) { array[i] = array[i-1]; } // put the new one in the right place array[index] = element; } ``` 這個雙參數的版本，叫做`add(int, E)`，它使用了單參數的版本，稱為`add(E)`，它將新的元素放在最后。然后它將其他元素向右移動，并將新元素放在正確的位置。 在我們可以劃分雙參數`add`之前，我們必須劃分單參數`add`： ```java public boolean add(E element) { if (size >= array.length) { // make a bigger array and copy over the elements E[] bigger = (E[]) new Object[array.length * 2]; System.arraycopy(array, 0, bigger, 0, array.length); array = bigger; } array[size] = element; size++; return true; } ``` 單參數版本很難分析。如果數組中存在未使用的空間，那么它是常數時間，但如果我們必須調整數組的大小，它是線性的，因為`System.arraycopy`所需的時間與數組的大小成正比。 那么`add`是常數還是線性時間的？我們可以通過考慮一系列`n`個添加中，每次添加的平均操作次數，來分類此方法。為了簡單起見，假設我們以一個有`2`個元素的空間的數組開始。 + 我們第一次調用`add`時，它會在數組中找到未使用的空間，所以它存儲`1`個元素。 + 第二次，它在數組中找到未使用的空間，所以它存儲`1`個元素。 + 第三次，我們必須調整數組的大小，復制`2`個元素，并存儲`1`個元素。現在數組的大小是`4`。 + 第四次存儲`1`個元素。 + 第五次調整數組的大小，復制`4`個元素，并存儲`1`個元素。現在數組的大小是`8`。 + 接下來的`3`個添加儲存`3`個元素。 + 下一個添加復制`8`個并存儲`1`個。現在的大小是`16`。 + 接下來的`7`個添加復制了`7`個元素。 以此類推，總結一下： + `4`次添加之后，我們儲存了`4`個元素，并復制了兩個。 + `8`次添加之后，我們儲存了`8`個元素，并復制了`6`個。 + `16`次添加之后，我們儲存了`16`個元素，并復制了`14`個。 現在你應該看到了規律：要執行`n`次添加，我們必須存儲`n`個元素并復制`n-2`個。所以操作總數為`n + n - 2`，為`2 * n - 2`。 為了得到每個添加的平均操作次數，我們將總和除以`n`；結果是`2 - 2 / n`。隨著`n`變大，第二項`2 / n`變小。參考我們只關心`n`的最大指數的原則，我們可以認為`add`是常數時間的。 有時線性的算法平均可能是常數時間，這似乎是奇怪的。關鍵是我們每次調整大小時都加倍了數組的長度。這限制了每個元素被復制的次數。否則 - 如果我們向數組的長度添加一個固定的數量，而不是乘以一個固定的數量 - 分析就不起作用。 這種劃分算法的方式，通過計算一系列調用中的平均時間，稱為攤銷分析。你可以在 <http://thinkdast.com/amort> 上閱讀更多信息。重要的想法是，復制數組的額外成本是通過一系列調用展開或“攤銷”的。 現在，如果`add(E)`是常數時間，那么`add(int, E)`呢？調用`add(E)`后，它遍歷數組的一部分并移動元素。這個循環是線性的，除了在列表末尾添加的特殊情況中。因此， `add(int, E)`是線性的。 ## 3.3 問題規模 最后一個例子中，我們將考慮`removeAll`，這里是`MyArrayList`中的實現： ```java public boolean removeAll(Collection<?> collection) { boolean flag = true; for (Object obj: collection) { flag &= remove(obj); } return flag; } ``` 每次循環中，`removeAll`都調用`remove`，這是線性的。所以認為`removeAll`是二次的很誘人。但事實并非如此。 在這種方法中，循環對于每個`collection`中的元素運行一次。如果`collection`包含`m`個元素，并且我們從包含`n`個元素的列表中刪除，則此方法是`O(nm)`的。如果`collection`的大小可以認為是常數，`removeAll`相對于`n`是線性的。但是，如果集合的大小與`n`成正比，`removeAll`則是平方的。例如，如果`collection`總是包含`100`個或更少的元素， `removeAll`則是線性的。但是，如果`collection`通常包含的列表中的 1% 元素，`removeAll`則是平方的。 當我們談論問題規模時，我們必須小心我們正在討論哪個大小。這個例子演示了算法分析的陷阱：對循環計數的誘人捷徑。如果有一個循環，算法往往是 線性的。如果有兩個循環（一個嵌套在另一個內），則該算法通常是平方的。不過要小心！你必須考慮每個循環運行多少次。如果所有循環的迭代次數與`n`成正比，你可以僅僅對循環進行計數之后離開。但是，如在這個例子中，迭代次數并不總是與`n`成正比，所以你必須考慮更多。 ## 3.4 鏈接數據結構 對于下一個練習，我提供了`List`接口的部分實現，使用鏈表來存儲元素。如果你不熟悉鏈表，你可以閱讀 <http://thinkdast.com/linkedlist> ，但本部分會提供簡要介紹。 如果數據結構由對象（通常稱為“節點”）組成，其中包含其他節點的引用，則它是“鏈接”的。在鏈表 中，每個節點包含列表中下一個節點的引用。其他鏈接結構包括樹和圖，其中節點可以包含多個其他節點的引用。 這是一個簡單節點的類定義： ```java public class ListNode { public Object data; public ListNode next; public ListNode() { this.data = null; this.next = null; } public ListNode(Object data) { this.data = data; this.next = null; } public ListNode(Object data, ListNode next) { this.data = data; this.next = next; } public String toString() { return "ListNode(" + data.toString() + ")"; } } ``` 該`ListNode`對象具有兩個實例變量：`data`是某種類型的`Object`的引用，并且`next`是列表中下一個節點的引用。在列表中的最后一個節點中，按照慣例，`next`是`null`。 `ListNode`提供了幾個構造函數，可以讓你為`data`和`next`提供值，或將它們初始化為默認值，`null`。 你可以將每個`ListNode`看作具有單個元素的列表，但更通常，列表可以包含任意數量的節點。有幾種方法可以制作新的列表。一個簡單的選項是，創建一組`ListNode`對象，如下所示： ```java ListNode node1 = new ListNode(1); ListNode node2 = new ListNode(2); ListNode node3 = new ListNode(3); ``` 之后將其鏈接到一起，像這樣： ``` node1.next = node2; node2.next = node3; node3.next = null; ``` 或者，你可以創建一個節點并將其鏈接在一起。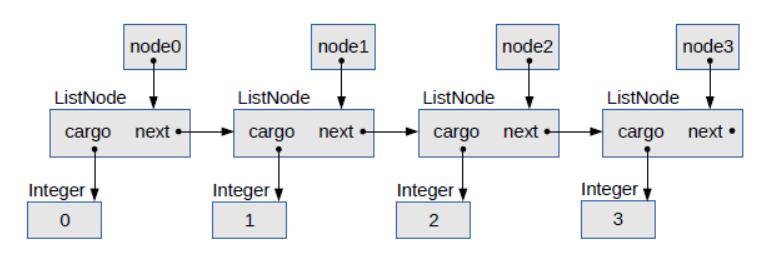例如，如果要在列表開頭添加一個新節點，可以這樣做： ```java ListNode node0 = new ListNode(0, node1); ```  圖 3.1 鏈表的對象圖 圖 3.1 是一個對象圖，展示了這些變量及其引用的對象。在對象圖中，變量的名稱出現在框內，箭頭顯示它們所引用的內容。對象及其類型（如ListNode和Integer）出現在框外面。 ## 3.5 練習 3 這本書的倉庫中，你會找到你需要用于這個練習的源代碼： + `MyLinkedList.java`包含`List`接口的部分實現，使用鏈表存儲元素。 + `MyLinkedListTest.java`包含用于`MyLinkedList`的 JUnit 測試。 運行`ant MyArrayList`來運行`MyArrayList.java`，其中包含幾個簡單的測試。 然后可以運行`ant MyArrayListTest`來運行 JUnit 測試。其中幾個應該失敗。如果你檢查源代碼，你會發現三條 TODO 注釋，表示你應該填充的方法。 在開始之前，讓我們來看看一些代碼。以下是`MyLinkedList`的實例變量和構造函數： ```java public class MyLinkedList<E> implements List<E> { private int size; // keeps track of the number of elements private Node head; // reference to the first node public MyLinkedList() { head = null; size = 0; } } ``` 如注釋所示，`size`跟蹤`MyLinkedList`有多少元素；`head`是列表中第一個`Node`的引用，或者如果列表為空則為`null`。 存儲元素數量不是必需的，并且一般來說，保留冗余信息是有風險的，因為如果沒有正確更新，就有機會產生錯誤。它還需要一點點額外的空間。 但是如果我們顯式存儲`size`，我們可以實現常數時間的`size`方法；否則，我們必須遍歷列表并對元素進行計數，這需要線性時間。 因為我們顯式存儲`size`明確地存儲，每次添加或刪除一個元素時，我們都要更新它，這樣一來，這些方法就會減慢，但是它不會改變它們的增長級別，所以很值得。 構造函數將`head`設為null，表示空列表，并將`size`設為`0`。 這個類使用類型參數`E`作為元素的類型。如果你不熟悉類型參數，可能需要閱讀本教程：<http://thinkdast.com/types>。 類型參數也出現在`Node`的定義中，嵌套在`MyLinkedList`里面： ```java private class Node { public E data; public Node next; public Node(E data, Node next) { this.data = data; this.next = next; } } ``` 除了這個，`Node`類似于上面的`ListNode`。 最后，這是我的`add`的實現： ```java public boolean add(E element) { if (head == null) { head = new Node(element); } else { Node node = head; // loop until the last node for ( ; node.next != null; node = node.next) {} node.next = new Node(element); } size++; return true; } ``` 此示例演示了你需要的兩種解決方案： 對于許多方法，作為特殊情況，我們必須處理列表的第一個元素。在這個例子中，如果我們向列表添加列表第一個元素，我們必須修改`head`。否則，我們遍歷列表，找到末尾，并添加新節點。 此方法展示了，如何使用`for`循環遍歷列表中的節點。在你的解決方案中，你可能會在此循環中寫出幾個變體。注意，我們必須在循環之前聲明`node`，以便我們可以在循環之后訪問它。 現在輪到你了。填充`indexOf`的主體。像往常一樣，你應該閱讀文檔，位于 <http://thinkdast.com/listindof>，所以你知道應該做什么。特別要注意它應該如何處理`null`。 與上一個練習一樣，我提供了一個輔助方法`equals`，它將數組中的一個元素與目標值進行比較，并檢查它們是否相等，并正確處理`null`。這個方法是私有的，因為它在這個類中使用，但它不是`List`接口的一部分。 完成后，再次運行測試；`testIndexOf`，以及依賴于它的其他測試現在應該通過。 接下來，你應該填充雙參數版本的add，它使用索引并將新值存儲在給定索引處。再次閱讀 <http://thinkdast.com/listadd> 上的文檔，編寫一個實現，并運行測試進行確認。 最后一個：填寫`remove`的主體。文檔在這里：<http://thinkdast.com/listrem>。當你完成它時，所有的測試都應該通過。 一旦你的實現能夠工作，將它與倉庫`solution`目錄中的版本比較。 ## 3.6 垃圾回收的注解 在`MyArrayList`以前的練習中，如果需要，數字會增長，但它不會縮小。該數組從不收集垃圾，并且在列表本身被銷毀之前，元素不會收集垃圾。 鏈表實現的一個優點是，當元素被刪除時它會縮小，并且未使用的節點可以立即被垃圾回收。 這是我的實現的`clear`方法： ```java public void clear() { head = null; size = 0; } ``` 當我們將`head`設為`null`時，我們刪除第一個`Node`的引用。如果沒有其他`Node`的引用（不應該有），它將被垃圾收集。這個時候，第二個`Node`引用被刪除，所以它也被垃圾收集。此過程一直持續到所有節點都被收集。 那么我們應該如何劃分`clear`？該方法本身包含兩個常數時間的操作，所以它看起來像是常數時間。但是當你調用它時，你將使垃圾收集器做一些工作，它與元素數成正比。所以也許我們應該將其認為是線性的！ 這是一個有時被稱為性能 bug 的例子：一個程序做了正確的事情，在這種意義上它是正確的，但它不屬于我們預期的增長級別。在像 Java 這樣的語言中，它在背后做了大量工作的，例如垃圾收集，這種 bug 可能很難找到。